响应面法在汽车侧面结构多目标优化中的应用

2022-07-18孙喜龙王登峰荣宝军李汝恒

机械科学与技术 2022年7期

孙喜龙,王登峰,荣宝军,李汝恒

(1.大理大学工程学院,云南大理 671003;2.吉林大学汽车工程学院,长春 130025;3.一汽-大众汽车有限公司,长春 130013;4.吉林工程技术师范学院机械与车辆工程学院,长春 130052)

汽车侧面碰撞是交通事故中一种常见的碰撞形式,但由于乘员的侧面可压缩空间小,发生侧面碰撞后,对乘员的保护作用相对较弱,侧面结构优化一直是学者的关注重点。为了提高汽车侧面结构的抗撞性能,国内外学者在汽车侧面碰撞领域进行多方面研究。

针对汽车B柱、车门等结构件进行优化,采用新材料,如热成型钢板[1-2]、泡沫铝[3-4]、碳纤维[5]等材料改善侧面抗撞性能;调整侧面结构刚度梯度[6]等方法对侧面抗撞性能进行分析;对气囊[7-9]、安全带[10]等部件进行优化设计,增强对乘员的保护;使用整车或简化仿真模型,研究汽车侧碰过程中,假人的伤害机理[11]等;上述研究侧重于零部件的优化,利用仿真和试验相结合的方法,进行单目标优化,其方案更依赖于开发者的设计经验。

随着数值模拟和优化理论的快速发展,许多学者在分析中引入近似模型和优化算法。Yildiz等[12]基于粒子群算法对车辆抗撞性能进行多目标优化,并对其有效性进行验证。周利辉等[13]采用拉丁方试验设计方法,结合BP神经网络和多目标遗传算法对汽车的侧面结构进行多目标优化,即提高了侧面结构的抗撞性能,又实现了车辆轻量化目标。Zhuang等[14]通过响应面近似模型,结合自适应加权的多目标优化对车身侧面结构进行多学科协同优化,提高侧面结构的抗撞性能。Xiong等[15]提出混合贡献度分析方法,对车身侧面结构的抗撞性能以及轻量化目标进行优化,验证混合贡献度分析方法的有效性。Wang等[16]利用Kriging近似模型和改进粒子群优化算法对汽车B柱结构进行多目标优化,提高了B柱的侧面抗撞性能。Zhou[17],使用新型填充负泊松比内芯的B柱结构,结合多项式响应面模型和遗传算法对B柱结构进行多目标优化,有效提高B柱抗撞性能。金浩等[18]通过响应面法,对轿车前保险杠结构进行多目标优化,有效提高前端结构的抗撞性能。王登峰等[19]利用径向基(RBF)近似模型和非支配遗传算法(NSGA-II)对B柱结构进行多目标优化设计,并对B柱多目标优化结果进行验证。由此可见,近似模型与优化算法的引入,使寻优过程更加简洁、快速、有效。

目前在汽车开发中,仍然采用仿真模型与试验验证相结合的分析方式,依靠设计经验,提出优化方案,虽然云计算的应用,极大地缩短了开发周期,但耗时5 h,去完成一个单元数为百万级的仿真模型,其计算效率是无法满足快速开发模式的要求;而且仅凭设计经验,寻找多目标的优化方案,更显力不从心,解的精度也无法保证。所以在汽车开发中,利用仿真分析数据,建立变量与响应的近似数学模型,进行多目标优化,兼顾计算效率和精度,必将成为主要的开发思路。

1 侧面碰撞模型验证

1.1 侧面碰撞评价指标

侧面碰撞试验主要考核车身侧面结构抗撞性及其对乘员的保护,车身侧面结构的变形直接影响车内乘员伤害程度。本文采用B柱4个测量点在Y向的侵入量、侵入速度,以及前、后车门的6个测量点在Y向侵入速度,作为侧面结构抗撞性能的评价指标,如图1所示。各测量点的具体位置需要与实际车身结构相结合,测量点位置应满足布置传感器的空间尺寸要求[20]。

图1 侧面碰撞评价参考点

1.2 侧面碰撞模型试验验证

根据试验数据,设定仿真壁障碰撞速度为50.4 km/h,计算仿真模型的100 ms侧面碰撞响应过程。如图2～图6所示,B柱各测量点的侵入量仿真结果与试验结果较为接近,侵入速度曲线变化趋势与试验结果吻合,但试验结果偏低,主要是仿真模型中没有考虑金属材料拉伸硬化的影响,车身刚度偏软,导致侵入速度均偏小。

图2 B柱侵入量

图3 B柱b1侵入速度

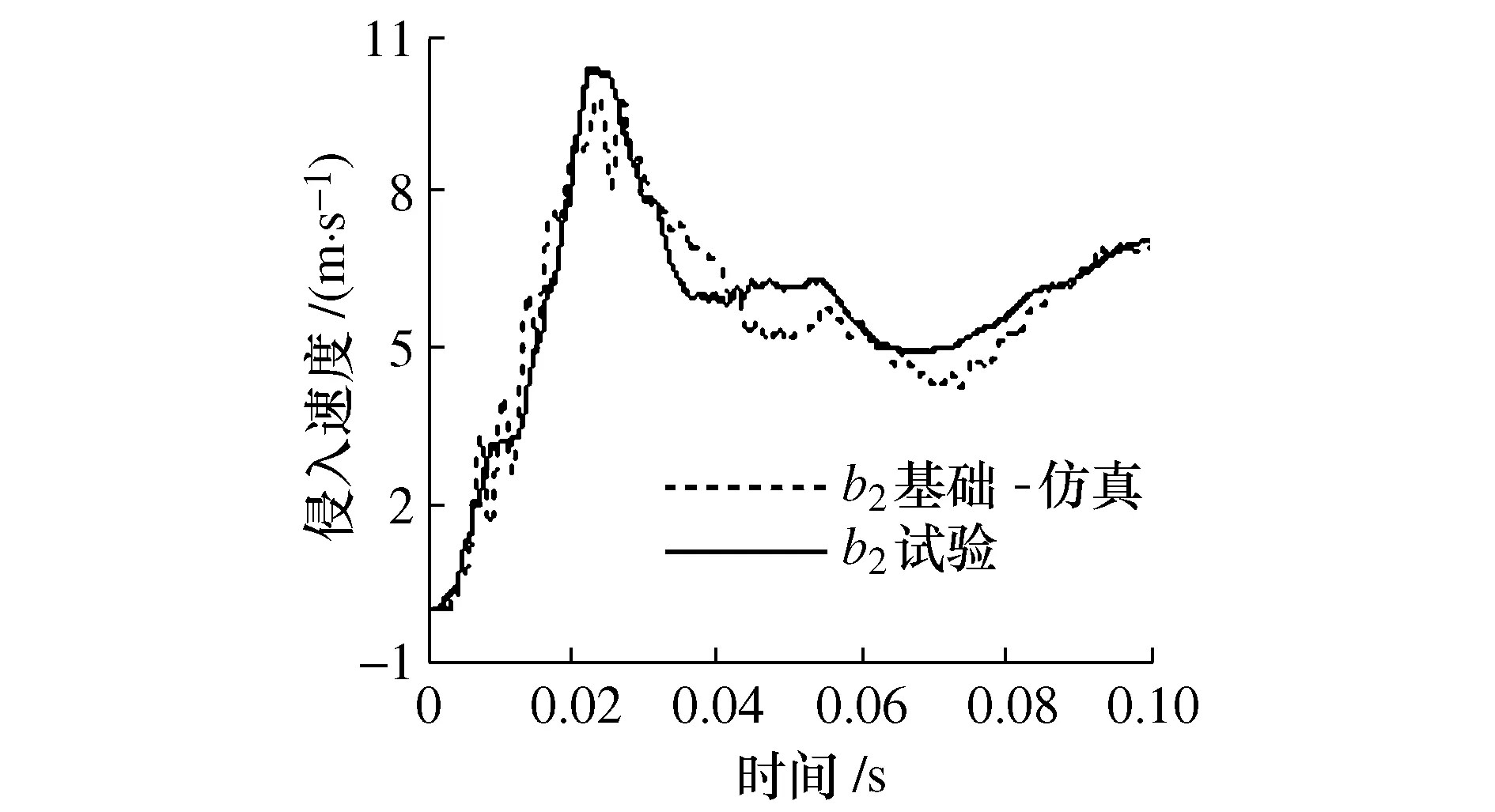
图4 B柱b2侵入速度

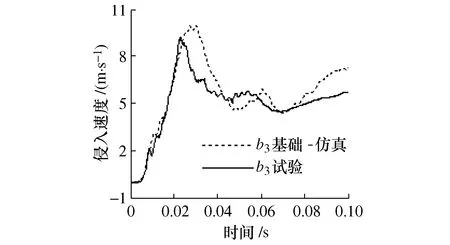
图5 B柱b3侵入速度

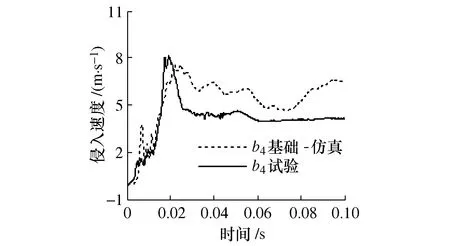
图6 B柱b4侵入速度

通过前门测量点侵入速度的对比(图7～图9),前车门测量点的侵入速度的曲线峰值、变化趋势均与试验结果相吻合。由于后车门传感器故障,导致后车门试验数据缺失,本文不做数据对比。

图7 前门TV1侵入速度

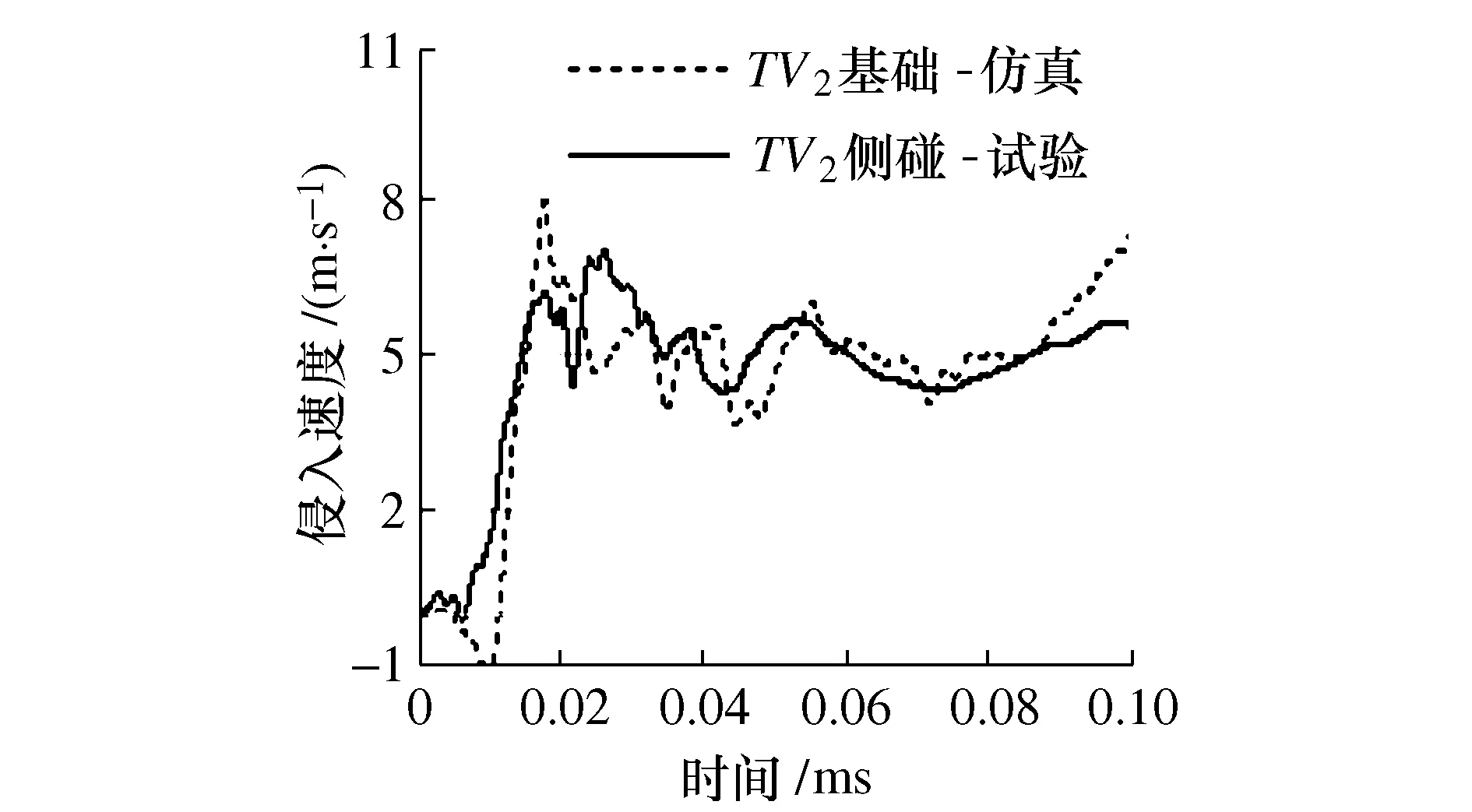
图8 前门TV2侵入速度

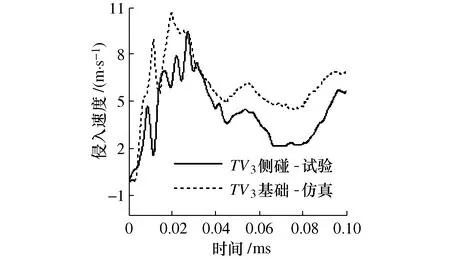
图9 前门TV3侵入速度

通过仿真和试验的侧面变形模式对比(图10),前后车门外板在壁障的撞击下,仿真与试验结果均呈现出向内凹陷,并紧贴于车门防撞梁和车门框;在后车门把手上方区域,以门锁为轴,向车身外侧张开。

图10 车门变形

通过对比,仿真模型能够准确的反应出侧面碰撞中的特性,模型精度达到工程分析要求,但车辆B柱的侵入量较大,车身的侧面结构需要进一步优化。

2 近似模型

2.1 设计变量

根据车身侧面结构数据,选取车身侧面8个零件的板厚(t1～t8)及5个零件的材料(m1～m5)作为设计变量(图11),其变量表达式

图11 设计变量结构图

X=[t1t2t3t4t5t6t7t8m1m2m3m4m5]T

(1)

设计变量板厚及材料信息如表1所示。

表1 设计变量取值范围

2.2 约束条件

进行多目标优化设计时,根据产品的设计要求,对设计变量和目标函数进行约束和限定。测量点的位置不同,其限定值也是不同的。

(2)

式中:db1、db2、db3、db4分别为B柱4个位置点的侵入量;Vb2、Vb3分别为B柱b2、b3位置点的侵入速度。

2.3 目标函数

将B柱4个位置点的侵入量以及b2、b3点的侵入速度和优化结构质量作为目标函数,目标函数表达式为

minyi=min{M,db1(x),db2(x),

db3(x),db4(x),Vb2(x),Vb3(x)}

(3)

式中:M为优化结构的总质量;d(x)为B柱侵入量函数;V(x)为B柱侵入速度函数。

2.4 拉丁超立方试验设计

拉丁超立方是研究多因素实验设计的常用试验设计方法,其样本点均匀分散在设计空间,能够反映整个设计空间的特性,具有效率高,均衡性能好的优点。本文利用拉丁超立方试验设计方法进行样本试验设计。

由于汽车用钢板和材料均按行业标准生产,钢板的厚度和材料均为离散变量,每个变量定义4个水平(表1)。在试验设计时,先将板厚和材料变量均看作连续变量处理,根据板厚变量的上下限值,进行线性插值;将4种材料按材料的屈服强度的大小顺序进行编码,即DC03,HC260LAD,HC340LAD,HC420/780DP分别对应a～d。选择拉丁超立方试验设计方法,样本数定义为200,输入设计变量及相应的上下限值,列出13个设计变量、200水平的样本矩阵。将样本矩阵导入excel表,将材料变量m1进行顺序排列,其它设计变量作为扩展区域,同步变化,将已排列的材料变量m1的200个样本点,按顺序10个一组,依次用4种材料进行替换,顺序循环,其它4个材料变量以此类推,组成新的13个设计变量、板厚为200个水平、材料为4个水平的试验矩阵。将每组设计变量导入仿真模型中进行计算,提取相应的响应值,从而得到200个变量-响应的样本数据。

2.5 3阶多项式响应面近似模型

多项式响应面模型可以较好的处理汽车碰撞的非线性问题,不论变量与响应之间的关系多么复杂,总可以利用多项式函数对问题进行近似描述。

3阶多项式响应面数学表达式为:

(5)

(6)

图12分别为db1、db2、db3、db4、Vb2、Vb3、M的3阶多项式响应面模型精度的散点图。

图12 各目标函数误差散点图

图12a)为db1响应面精度的散点图,横坐标为响应面的预测值,纵坐标是在同一组设计变量条件下,仿真模型计算得到的实测值;其中对角线为响应面理想状态的拟合位置点,表示响应面模型有100%的拟合精度;水平线为实际响应值的平均值。预测位置点,越接近对角线位置,代表响应面模型精度越高。预测点越接近响应值的平均值,代表设计变量的不同组合,对响应的影响程度越小,目标函数对变量的敏感度越小。如表2所示,7个响应面的决定系数,均大于85%,响应面模型的拟合精度均满足工程分析要求。

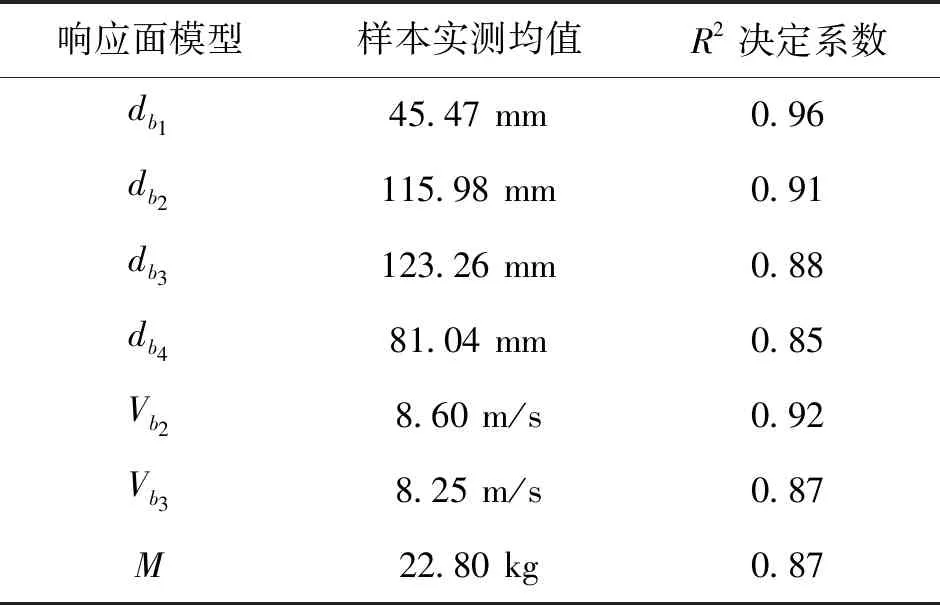
表2 3阶响应面模型的决定系数

3 多目标优化求解

3.1 自适应模拟退火优化算法

模拟退火算法的数学描述为:在给定邻域内,模拟退火过程是从一个状态到另一个状态不断随机“游动”,这个过程可用马尔可夫链来描述。当温度t为一定时,两个状态的移动概率定义如下:

(7)

式中:|D|表示状态集合中状态的个数;Aij(t)是接受概率,表示在状态i产生j后,接受j的概率,Aij不总是等于1,即状态也有不被接受的可能。算法停留在状态i的概率为

(8)

式中:Pij是下一步转移概率;Gij是从i到j的产生概率,表示在状态i时,j状态被选取的概率,可以理解j是i的邻域。

模拟退火过程中接受概率为:

(9)

式中f(j)为第j状态下的目标函数值。

Δfij=f(j)-f(i)

(10)

优化分析时设置最大迭代次数为10 000,收敛检查间隔设置为5,如果相邻连续5次的残差都比收敛准则的参数小,则优化终止。收敛准则σ≤1.0×10-8,每次执行的可行解和当前最优解间的最大差值,表征是否收敛。所有设计变量均按离散变量处理,板厚设计变量按表1的4个取值点进行设定、材料变量按可选材料牌号对应的编码进行设定。各目标函数的优化迭代历程如图13所示。

图13 各目标函数的迭代历程

近似模型优化经历了235次迭代,得到235个设计方案,有192个可行方案(黑色圆点)满足设计要求,其中有29个为Pareto解(蓝色圆点)。当一个优化方案点超出约束条件的上下限时,将其定义为非可行方案,在优化历程曲线中,用红色圆点表示,有42个非可行方案不满足约束条件。图13中红色和蓝色水平线分别为约束条件的上下限值。

3.2 优化结果对比分析

由于优化过程中,对设计变量按离散变量处理,取值点非连续,导致Pareto解比较分散,没有形成明显的Pareto前沿,但变量的离散处理后,每个可行优化解对应的设计变量,均对应实际的材料和常用的板厚,优化方案更具有实际意义。参照各响应的迭代历程以及优化方案参数统计表,从Pareto解集中选择综合性能最优的方案。最优设计点选择原则如下:

1) 优化设计方案的模型质量尽可能的小。

2) 在约束条件内,在侵入量,侵入速度尽可能小的前提下,尽量选用零件板厚值小、材料的屈服强度低的方案,以降低材料成本。

经过综合比较,选第223步迭代优化点作为最优方案。根据优化方案的设计变量信息,组建侧面碰撞有限元模型,同时为了与初始模型进行更详细的对比分析,在优化模型中加入了假人模型。表3列出了最优方案的仿真结果和近似模型的预测值,通过数值的对比,近似模型对目标函数预测的最大相对误差7.9%。

表3 初始、优化方案仿真结果及近似模型计算结果

对比初始方案与优化方案仿真结果,根据车身侧面侵入量云图(图14),优化后的车身侧面抗撞性能,明显好于初始方案;同时结合表3数据,B柱侵入量均低于初始结果,b4位置点,下降了62%,可见在B柱和门槛位置使用高强度钢板可以有效改善侧面结构的侵入量。

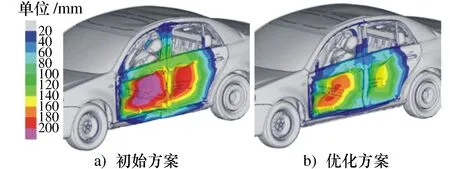
图14 车身侧面变形

B柱各位置点的侵入速度如图15所示,b2、b3位置点最大侵入速度分别下降26%和29%,而且峰值对应时刻向后延迟近20 ms,更有利于对假人的保护;b4位置点的侵入速度由初始方案的7.5 m/s下降到6.0 m/s,下降20%,曲线的变化趋势和峰值时刻向后延迟,与b2、b3位置点侵入速度曲线相似,可见对车身侧面结构的优化设计,更好的保证车身侧面刚度分布的均匀性。b1位置点的侵入速度由初始状态的5.7 m/s提高到6.6 m/s,主要原因是由于B柱、门槛区域采用高强度钢板及部分零件增加了板厚来提高此区域的整体刚度,但对车身侧面碰撞起支撑作用顶盖横梁以及前后门洞的顶盖区域的零件均没有进行优化,当侧面刚度增加后,此位置的刚度相对变弱,导致b1点的侵入速度提高。虽然此点的侵入速度变大,但在设计要求范围内,此结果可以接受。

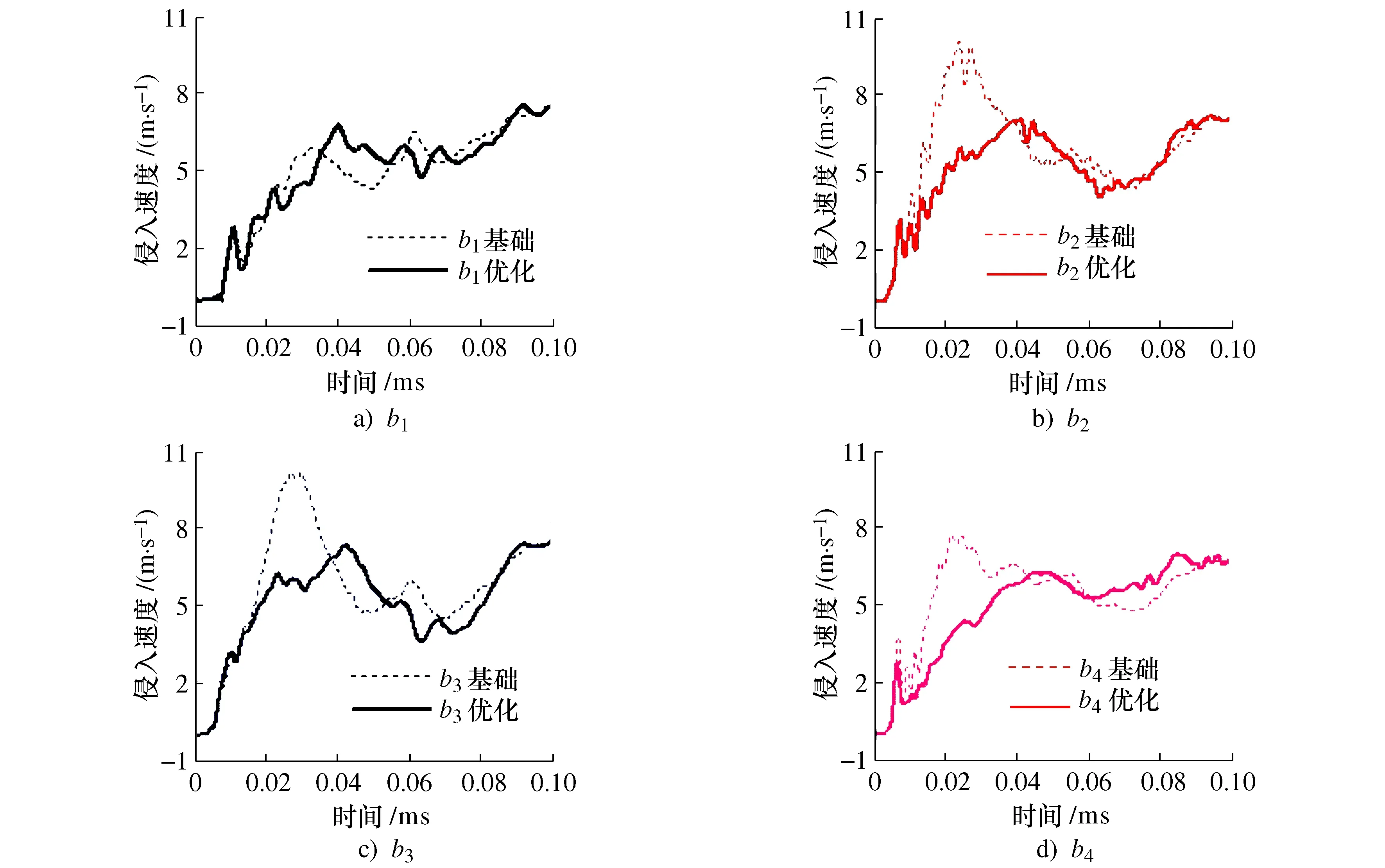
图15 B柱侵入速度

图16为车门侵入速度曲线对比,前车门3个位置点的侵入速度均下降,曲线在18 ms前,没有明显的变化,曲线的变化趋势相似,18 ms后下降明显,这是因为在碰撞的初始阶段,门外板先接触移动可变形壁障,发生挤压变形,当受到壁障继续挤压时,由于前门通过A柱两个铰链及B柱门锁将前门固定和锁止,前门将A柱和B柱连接起来,当B柱刚度提高时,车门侵入速度会下降;当壁障继续挤压时,车门、B柱和门槛区域的侵入速度将同步变化。

图16 车门测量点侵入速度

在碰撞的40 ms后,B柱和前门的侵入速度曲线变化趋势极为相似。后车门TH1的侵入速度由优化前8.8 m/s下降至7.6 m/s,TH2在40 ms左右,侵入速度由优化前7.0 m/s下降至6.1 m/s。在40～60 ms的碰撞过程中,TH1和TH2位置点的优化后侵入速度曲线先下降再上升,主要因为壁障与TH1和TH2点相对位置关系,以及后车门锁的原因,使后门门锁上部区域在碰撞过程中,以门锁为轴向外旋转变形造成的。

通过初始方案和优化方案的假人仿真结果对比(图17),假人的HIC、3 ms加速度、胸部压缩量、T12的Y向力、腹部力、耻骨力都明显改善;假人的胸部压缩量由原来的28.49 mm下降至21.32 mm,从而避免了对假人胸部的扣分,大大降低了司机胸部的伤害。在初始方案中,假人T12的Y向力数值较大,造成该项被评0分,优化后该项数值明显改善,提升了假人该部位的保护能力。根据假人腹部力与假人耻骨力仿真结果,初始方案的数值较大,优化后该项数值明显改善,提升了假人腹部和骨盆部位的保护。可见通过多目标优化提高了该车型侧面结构对乘员的保护能力,降低了重伤及死亡的概率。