低轨卫星自跟踪状态稳定性分析

蓝廷帅

(成都天奥集团有限公司，四川 成都 611730)

0 引言

目前，业内主要采用单通道自跟踪控制的方法，分析低轨卫星自跟踪状态稳定性[1]。在不同的跟踪模式和干扰情况下，对常见的S和X频段的低轨卫星状态特征进行稳定性分析，提高低轨卫星自跟踪状态稳定性和控制能力。基于此，本文提出了一种单通道自跟踪情况下对S和X频段的低轨卫星状态稳定性跟踪控制方法。首先构造在不同频段下低轨卫星自跟踪状态参数识别模型，然后通过非线性系统控制的方法，进行稳态误差补偿设计，建立S和X频段单通道跟踪的信道稳定性分析模型，结合非线性不确定扰动补偿方法，实现低轨卫星自跟踪状态稳定性分析。通过仿真测试分析，表明本文方法在提高低轨卫星自跟踪状态稳定性分析和控制能力方面具有优越性。

1 模型构建和参数分析

卫星地面站是卫星通信系统中重要组成部分，地面站通过测控天线发射和接收低轨卫星信号，分析信号参数实现卫星控制和数传接收。但在实际发射和接收信号时，由于地面温度不定、线缆长度不一、设备单机不稳定等因素，会引起卫星信道偏移，导致单通道自跟踪不稳定。所以，需要构建约束参数模型对单通道自跟踪稳定性进行控制[2]。

1.1 模型构建

为了实现单通道低轨卫星自跟踪状态稳定性控制，采用运动平台坐标系下的角度测量及参数分析方法，构建载体坐标系下的运动学规划模型，基于运动学分析方法进行单通道低轨卫星自跟踪状态稳定性过程中的约束侧偏角参数调节，结合信号寻优和模糊度检测方法，进行载体坐标系下的收敛性控制，采用DSP进行跟踪滤波和定位设计，得到DDC数字下变频和滤波处理的参数自适应寻优模型。根据单通道低轨卫星自跟踪装置的运动参数模型构造，构建单通道低轨卫星自跟踪装置主动单通道状态跟踪分析模型，采用自适应的单通道状态跟踪梯度网格分级控制方法实现单通道低轨卫星信道偏移控制，得到参数寻优公式：

(1)

式中，g′(odq)为单通道低轨卫星自跟踪装置移动的偏移修正系数，zdj为目标角度信息参数，ajq为判决门限，zkj为常数。假设odq为单通道低轨卫星自跟踪装置驱动控制智能参数，ajq是某时刻波束指向性参数，得到波束指向估计信息传递参数，进而得到卫星自跟踪的天线运动范围为：

X(R)=X(n)-yc(-1)i+1

(2)

其中，X(n)为天线接收增益的偏移量，yc为二维有源相控阵列参数，i为测试次数，由此，构造在不同频段下低轨卫星自跟踪状态参数识别模型。

1.2 控制约束参数分析

构造的正定函数，采用低轨卫星自跟踪状态参数控制器，建立周期性互联引导作用下的单通道低轨卫星自跟踪状态稳定控制模型，通过主动单通道状态跟踪控制过程中的路径寻优和收敛性控制，得到单通道低轨卫星自跟踪状态稳定寻优目标函数为：

f(i)=(aij)n×n

(3)

其中，aij为状态变量，n为惯性联合控制参数，单通道低轨卫星自跟踪装置移动跟踪控制的自适应学习权值pij定义为：

(4)

2 低轨卫星自跟踪状态稳定控制

为了有效控制单通道低轨卫星自跟踪的稳定性，依据上述构建的约束参数模型，对低轨道卫星的单通道控制稳态特征量进行分析，达成信道均衡效果。通过末端位置补偿方式可以稳定低轨卫星自跟踪系统状态，增强发射和接收低轨卫星信号能力，以提高低轨卫星工作效率。

2.1 S和X频段的单通道控制

τij(t+n)=(1-ρ)τij(t)+Δτij(t)

(5)

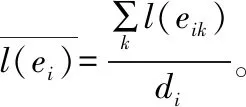
其中，l(eik)为周期性空间互联惯性参数，di为卫星系统在空间的位置信息，k为位置精度。由此建立低轨道卫星跟踪控制的单通道控制模型。

2.2 控制稳定性优化

结合非线性不确定扰动补偿方法，实现低轨卫星单通道自跟踪过程中的信道均衡控制，建立较为准确的映射关系，得到单通道低轨卫星自跟踪装置移动路径寻优的空间三维坐标分布节点va，vb和vc，通过迭代的方式实现单通道低轨卫星自跟踪装置的末端位置补偿，得到初始权值和阈值路径寻优的分形指向性函数为：

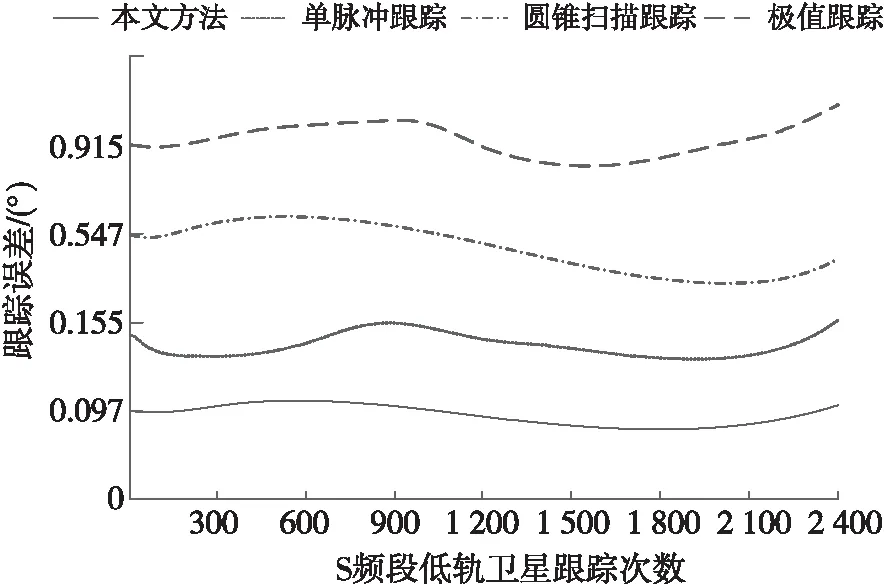
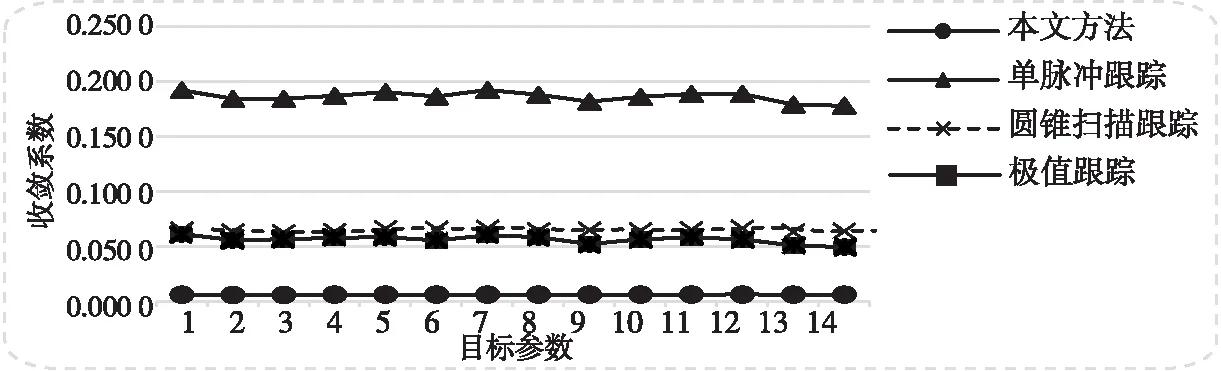
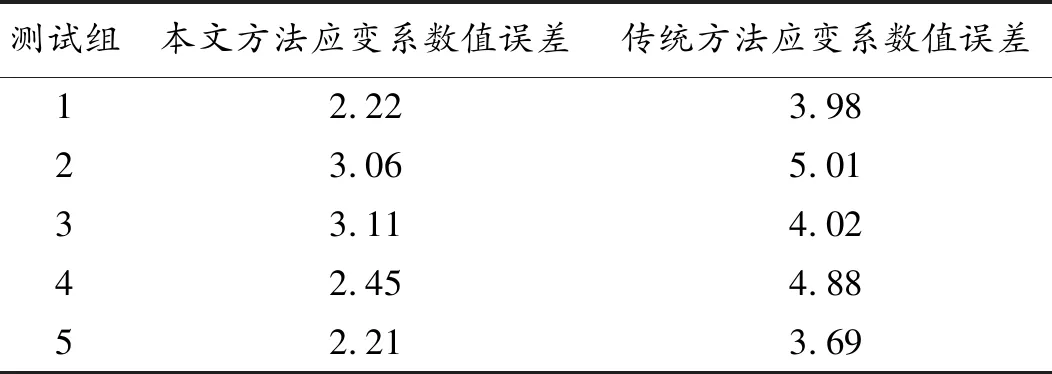
RIa=max(Xk，a)-min(Xk，a)，1

(6)

minF=(x，y)2+Z

(7)

其中，(x，y)表示二维分布坐标系，Z表示非几何参数误差，采用稳定性边界调节方法，得到单通道低轨卫星自跟踪的误差调整微分方程为：

(8)

(9)

其中：

(10)

(11)

式中：E为低轨卫星自跟踪系统的状态分布权重系数；Si为非几何参数误差；Ai为可观测性指标。

综上分析，根据低轨卫星自跟踪系统的状态、输入和输出等参数表现，采用稳定性控制和反馈跟踪误差补偿，实现卫星自跟踪状态稳定性分析和改进。

3 仿真测试分析

为了验证所提低轨卫星自跟踪状态稳定性算法的有效性，拟定在Matlab R 2019 b主频为1的环境下进行仿真。通过仿真验证本文方法在实现低轨卫星在单通道自跟踪情况下对低轨道卫星的状态稳定性。

分别对同一颗低轨道卫星的S频段和X频段进行多次跟踪，分析自动跟踪完成以后的跟踪稳定，测试本文方法与单脉冲跟踪、圆锥扫描跟踪、极值跟踪分析准确性，对比结果如图1～2所示。

分析图1、图2可知，本文方法跟踪误差稳定保持在0.1°以内，波动幅度较小。而单脉冲跟踪误差为0.155°和0.103°，圆锥扫描误差为0.547°和0.401°，极值跟踪误差为0.915°和0.802°，且波动幅度较大。进行不同跟踪方式下的稳定性的测试，得到稳定性测试结果如表1和表2所示。

图1 S频段准确性结果

图2 X频段准确性结果

分析表1和表2得知，本文方法进行低轨卫星在单通道自跟踪的稳定性较好，测试稳定收敛性曲线，如图3所示。

表1 不同跟踪方式下S频段低轨卫星跟踪稳定性测试结果

表2 不同跟踪方式下X频段低轨卫星跟踪稳定性测试结果

图3 收敛性测试

分析图3得知，本文方法进行单通道低轨卫星自跟踪状态稳定性设计的收敛性较好。

低轨卫星自跟踪状态稳定性主要由输出电流与电压波形决定。采用Matlab/Simulink工具箱，依据测试准备参数，分别利用PI控制器与本文控制器对低轨卫星自跟踪状态进行控制测试，通过测试得到电流波形测试结果如图4所示。

图4 电流波形测试结果图

如图4所示，PI控制器输出电压幅值为275 V，而本文控制器输出电压幅值为125 V，说明本文控制器对电压具有明显的抑制作用，电压幅值降低了54%。

上述测试结果显示：低轨卫星自跟踪状态电压幅值降低了54%，电流正弦性增加，充分说明本文方法具备更好的稳定性。

通过对比随机导入10组动态数据的稳定性结果误差量，来证明该设计的有效性。具体参量详见表3、表4所示。

表3 稳定性分析应力误差测试

表4 稳定性分析应变系数误差测试

通过表3、表4数据结果对比综合分析，可证明本文方法更具稳定性以及精准度，可以满足设计要求。

4 结语

在不同的跟踪模式和干扰情况下，对低轨卫星的跟踪系统信道的状态特征进行稳定性分析，提高低轨卫星自跟踪状态稳定性和控制能力，本文提出基于单通道自跟踪情况下的低轨卫星S和X频段的信道状态稳定性控制方法。测试得知，本文方法进行卫星低轨自跟踪控制的准确性、稳定性和收敛性较好。