活动视角下基于家庭出行时通勤者的出行方式选择研究

兰招娣，田丽君

(福州大学经济与管理学院，福建 福州 350116)

1 研究背景

近年来，随着城市化进程的不断加快以及人民生活水平的提高，交通拥堵问题日益突出，如何缓解交通拥堵已经成为相关研究人员以及国家政府的重点关注对象，而通勤者的出行行为在其中扮演着至关重要的角色。1969年，Vickrey[1]应用确定性排队理论推出瓶颈模型，由于瓶颈模型能够清晰明确地反映通勤者的出行特征，之后有不少学者将其作为研究的理论基础，从不同维度对用户出行行为展开了更加深入全面的分析。Smith[2]基于用户同质的假设，给出了在含有单个瓶颈中存在均衡到达模式的条件。Kuwahara[3]假设高速公路上含有两个瓶颈，得到均衡条件下含有双瓶颈的用户累计到达曲线。van den Berg 和Verhoef[4]研究了用户时间价值异质性对拥挤收费策略以及社会福利的影响。肖玲玲等[5]分析了通行能力的异质性对通勤者均衡出发时间选择以及均衡成本的影响。肖玲玲和黄海军[6]在用户异质的背景下，提出用收取信用券来替代拥挤收费，研究这一计划对用户均衡效益的影响。Liu和Nie[7]研究用户早高峰通勤行为及其对交通经济学的启示。王伟和孙会君[8]设立了3种维度的参考系，研究用户依赖不同参照偏好时对均衡模型以及道路拥挤收费策略的影响。

以上都是从单模式出行的角度进行研究分析。Tabuchi[9]研究实施在不同收费策略下私家车与地铁的竞争情况以及社会福利的变化。朱玲和卢晓珊[10]从自动驾驶汽车与传统私家车的差异性出发，讨论分析双模式混合交通流下的早高峰出行行为。周晶[11]就随机交通均衡配流问题给出了详细的推导演算，证明该问题可以表述为变分不等式问题，并给出了具体数学证明。Lu等[12]将Logit模型应用于出行模式选择问题中，研究3种出行模式并存时的最优收费策略。马超群等[13]利用Logit模型，用广义费用函数来代替模型中效用函数，研究常规公交与轨道交通的客流分配情况。张荣花等[14]基于共享汽车、出租车以及地铁三种出行模式的交通系统，构建多项Logit模型，针对用户出行方式选择的影响因素进行敏感性分析。田丽君等[15]研究不同交通管理策略组合对出行模式选择以及系统成本的影响。Li和Zhang[16]考虑活动效用，研究私家车和地铁共存的交通系统中用户均衡与拥挤收费定价策略。王景鹏和黄海军[17]研究了私家车与公共交通并存的交通系统下，利用可交易道路许可证政策将拥挤成本内部化，研究该策略对社会福利以及方式划分的影响。

以上研究都是基于个人的出行情形进行分析。实际上，大多数的早高峰通勤不仅是基于单个通勤者的目的地，而是基于家庭成员的多目的地的通勤：即家庭通勤是包括孩子上学以及家长上班的通勤行为。Jia等[18]分析了基于家庭出行的出发时间选择和均衡出行调度问题，考察高峰时段的最优收费策略。Zhang等[19]聚焦于学校临近工作场所的情形，研究学校地点的设立对家庭出行模式选择的影响。周城溪和肖玲玲[20]考虑个人通勤者和家庭通勤者共存时，研究通勤者的均衡出发模型以及路线选择问题。

本文考虑一个典型的家庭出行模型，即家庭出行者从家出发需要先将孩子送到学校上课，然后再到达工作地上班。家庭出行者面临两种出行方式，一为选择地铁通勤，二为选择自动驾驶汽车通勤。在此背景假设基础上，考虑活动效用，构建早高峰家庭出行均衡模型，分析家庭通勤者的出行方式选择。在均衡状态下进一步分析学校与工作地准时到达时间间隔、地铁平均发车时间间隔以及地铁票价对方式划分结果以及系统净效益的影响，从而设置合理取值来实现系统净效益最优化。

2 模型描述

下面分别对家庭通勤者选择无人驾驶汽车出行以及选择地铁出行时的情形进行分析。

2.1 选择地铁通勤的出行净效用

(1)

令CT(t)表示t时刻家庭通勤者选择地铁出行时整个家庭所付出的总成本，则有：

(2)

由式(1)和式(2)可计算整个家庭在出行期间所获净效用φT(t)为：

φT(t)=UT(t)-CT(t)

(3)

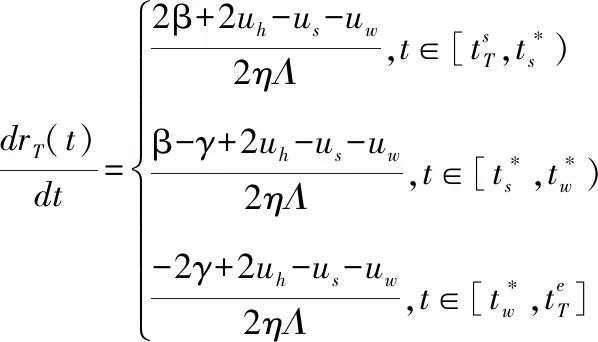
(4)

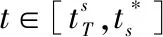
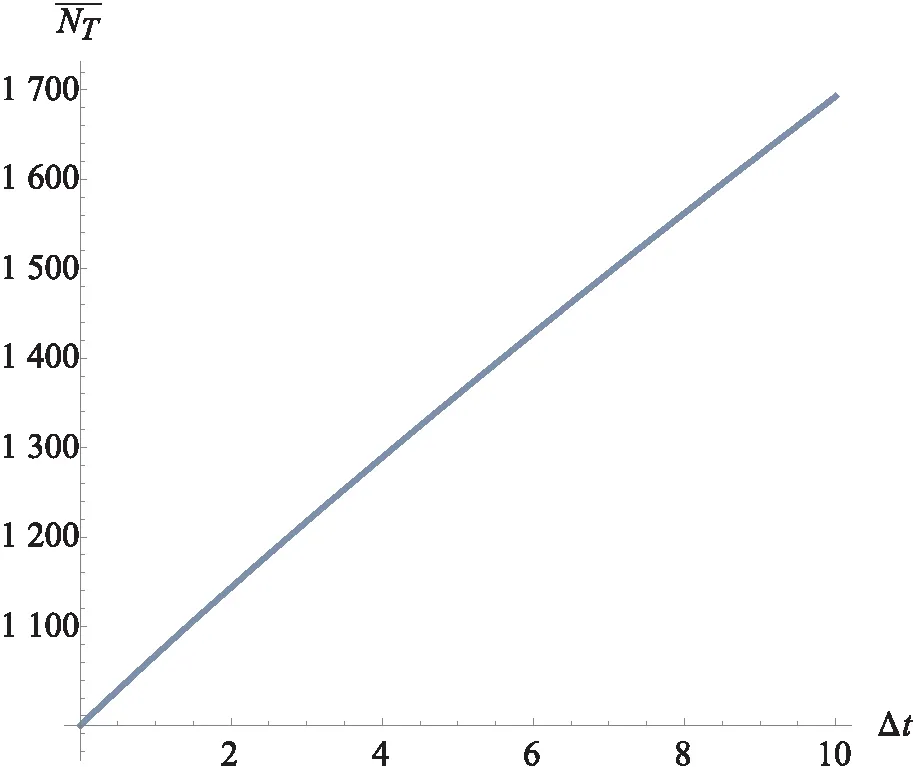
证明：由本文基本前提假设条件：γ>α>2β，uh

定理3：在出发时间段内，选择乘坐地铁的家庭通勤者的出发率在区间内是连续的。出发率如下：

(5)

(6)

(7)

(8)

(9)

2.2 选择自动驾驶汽车出行净效用

(10)

令CA(t)表示t时刻家庭通勤者选择自动驾驶汽车出行时整个家庭所付出的总成本，则有：

(11)

其中，t+T(t)表示到达目的地的时间点，pA表示自动驾驶汽车的路上消耗成本，包括所耗汽油成本，车身损耗成本等。

由式(9)和式(10)可计算选择自动驾驶汽车的家庭通勤者所获得的总效益φA(t)为：

φA(t)=UA(t)-CA(t)

(12)

(13)

(14)

(15)

(16)

当交通系统达到动态平衡时，每组家庭出行所获得的净效用都相等，且无法通过改变出发时刻来提升净效益。由每种出行情况给出的出发率函数，可以得出下面定理。

定理4：当且仅当家庭边际活动效用满足(us+uw-2β)/2≤tuh≤us+uw时，瓶颈处出现排队现象。

为方便讨论，本文均在排队现象存在的前提下进行分析。均衡状态下，各个出发时刻家庭净效益相等，第一个出发的家庭与最后一个出发的家庭均不参与排队，但将承担较高的计划延误成本。即有：

(17)

在出发时间段内，所以家庭成员完成通勤到达目的地。即有：

(18)

由式(16)、式(17)可解出最早出发时刻以及最晚出发时刻。

(19)

从式(19)中可以看出，随着Δt的增大，家庭通勤的最早出发时间将会向后推移，即家庭通勤者倾向于更迟出发。该结论与家庭成员选择地铁通勤时的情形保持一致。形成此种现象的原因也与家庭成员选择地铁通勤时同理。

(20)

由式(20)可知，在自动驾驶汽车出行系统中，其家庭均衡净效益与Δt是不相关的。

3 模型均衡结果与性质

(21)

其中，v=2β+a，Z=(2(uh-γ)β)(a+2γ)，B=(us+uw)，w=a+2γ，A=(γ+β)，Δp=pa-pT，为符合实际情况，Δp>0应成立，Y=(γ+β)((γ+β)(us+uw)-(a+2γ)β)，D=-AvZ2Δt+4Zv(ZN+B(wγ+A2sΔt)-Asw(Δp+βΔt))ηΛ+16Y2η2Λ2，式中最终符号正负由各参数的具体取值确定。将公式(21)分别回带至式(9)与式(20)，即可求得系统均衡状态下基于地铁出行系统以及基于自动驾驶出行系统时的家庭均衡净效益。此时整个交通出行系统总效益为：

(22)

4 算例分析

(23)

由式(23)可知，整个系统净效益与系统中选择自动驾驶汽车通勤家庭数量成正比，与选择地铁通勤家庭数量成反比。即系统净效益取最大值等效于选择地铁通勤家庭数量取最小值。

图1为准时上课时间点与准时开始工作时间点之间的时间间隔对交通出行方式划分的影响趋势。从图中可以看出，随着两地准点上学(上班)的时间间隔增大，会有更多的家庭从原来的自动驾驶汽车出行转向地铁出行，这是由于地铁出行的准点率相对于自动驾驶汽车出行方式较高，尤其是在出行基数较大的情形下。人们为了避免交通拥堵而造成计划延误，将会选择地铁出行来降低通勤成本，从而提升家庭净效益。

图1 准时上学(上班)时间间隔对地铁通勤家庭数量的影响

图2为地铁平均发车时间间隔对交通出行方式划分的影响趋势。从图中可以看出，随着发车时间间隔的增大，选择地铁出行的家庭数量先是急剧减少，当发车间隔Λ=2.65时，选择地铁出行家庭数量达到最低值856组。当平均发车时间间隔超过这一临界值，地铁出行家庭数量将不断增加。当平均发车时间间隔较小时，此时地铁发车数量较多，因此在车厢内的乘客对拥挤的敏感度较低，即不舒服成本较低。当平均发车时间间隔较大时，此时地铁发车数量较少，由于车厢内人数变多，乘客就需要承受较高的不舒服成本。但发车时间间隔越大，意味着发车时间点的信息是越明确的，即乘客将能够更加精准地选择出发时间，从而减少计划延误成本。

图2 地铁平均发车时间间隔对选择地铁通勤家庭数量的影响

图3为自动驾驶汽车路上消耗成本与地铁票价的差值对交通出行方式划分的影响趋势。从图中可以看出，当自动驾驶汽车路上消耗成本固定时，随着Δp增大，即随着地铁票价的降低，选择地铁通勤的家庭数量先减少，后增加，直到Δp=1.7元时，选择地铁通勤家庭数量达到最低点352组。上述结果也意味着整个系统达到净效益最大。此时最优的系统净效益为162 460元。总体来看，当地铁票价较高时，选择地铁通勤家庭数量是偏少的。当票价低于临界值之后，地铁票价对方式划分的结果影响更加明显。即随着地铁票价降低，选择地铁通勤家庭数量增加。

图3 自动驾驶汽车消耗成本与地铁票价差值对选择地铁通勤家庭数量的影响

5 结语

基于无人驾驶汽车和地铁出行的双模式情形，引入家庭通勤者，从活动效用的角度来分析家庭通勤者的出行选择。考虑无人驾驶汽车的特殊性引入了时间价值降低系数。分析了学校准时上课与工作地准点上班时间间隔、地铁平均发车时间间隔以及地铁票价对方式划分结果的影响趋势。结果发现：在系统处于均衡状态下，选择地铁通勤的家庭数量随着两个目的地准点开始的时间间隔增大而增大，随着地铁平均发车时间间隔的增大先减小，达到最小值之后后再增大，随着自动驾驶汽车消耗成本与地铁票价差值的增大先减少，在达到最小值之后再增大。在系统均衡状态下，存在一个最优的地铁平均发车时间间隔以及最优的地铁票价，令系统净效益达到最大值。相关政府可以通过调控上述关键参数来实现通勤者从无人驾驶汽车出行到地铁出行的引流，减少选择自动驾驶出行人数，从而缓解交通拥堵以及交通环境污染等情况，实现绿色交通出行。该结论能够给政府对与交通有关的决策提供一定的帮助。

下一步将研究实施最优收费策略来消除排队造成的拥堵成本，利用收费来调控出行方式划分的结果；考虑若将这部分收费以电子路票的方式返还给通勤用户，将对最终方式划分结果又有何具体影响，以期得出更加具体、明确的解析解，以更好地支撑研究内容，并得出更加有意义的研究结论。