基于抛物线形库仑-莫尔准则的板柱节点冲切承载力计算模型

2022-07-16孙俊豪费正玉梁诗雪

水利规划与设计 2022年8期

孙俊豪，费正玉，梁诗雪

(浙江理工大学建筑工程学院，浙江杭州 310018)

板柱结构以楼板和柱子作为承重体系，楼板下没有梁，降低了建筑物的层高，在地下停车场、仓库、多层厂房等被广泛应用。板柱的冲切破坏是工程设计中经常遇到的问题，一旦节点处受到冲切破坏，便会引起周边节点应力重分布，引发连续的坍塌事故，因此对板柱节点的抗冲切承载力的研究尤其重要。根据GB 50010—2010《混凝土结构设计规范》[1]计算得到的承载力结果与实际结果仍有一定误差，且没有考虑纵筋配筋率对冲切承载力的有利影响。国内外学者对板柱节点的破坏强度进行了大量试验研究，提出了许多冲切承载力计算方法。蒋大骅[2]基于刚塑性破坏模型，提出了抛物线形的库仑-摩尔混凝土破坏准则，但并未考虑配筋率的影响。严宗达[3]基于双剪强度理论对钢筋混凝土板轴对称冲切破坏强度进行了计算，用虚功方程求得破坏荷载的上限解。杨秀敏等[4]和魏雪英等[5]采用同统一强度理论，考虑了中间主应力效应，求解了轴对称混凝土板的冲切破坏强度。易伟建等[6]基于抛物线形库仑-莫尔破坏准则，推导了混凝土板柱受冲切承载力最小上限解。

为给出可解释的冲切承载力计算模型，本文基于抛物线形库仑-莫尔混凝土破坏准则，采用刚塑性破坏模型，引入了纵筋配筋率和销栓作用对板柱冲切的影响，推导建立混凝土板柱冲切承载力计算模型，与多国规范的计算结果对比，证明本文公式的准确性。

1 冲切承载力计算

将板柱节点冲切破坏的承载力分为3个部分，分别是混凝土部分提供的承载力、钢筋销栓作用提供的承载力和钢筋拉力提供的承载力。由虚功原理可得，板柱破坏时外力做功等于板柱节点内力做功：

P·u=Wc+Wb+Wst

(1)

式中，P(N)—外部荷载；u(m)—冲切体发生的虚位移，Wc(J)—混凝土部分做的内虚功；Wb(J)—钢筋销栓作用做的内虚功；Wst(J)—钢筋拉应力做的内虚功。

1.1 混凝土部分提供的承载力

采用塑性理论计算板柱结构的承载力，混凝土采用抛物线形Coulomb-Mohr破坏准则如图1所示。

图1 抛物线型Coulomb-Mohr准则

抛物线的包络线方程为：

(2)

(3)

(4)

式中，σn—屈服面上的正应力，MPa；τnt—屈服面上的剪应力，MPa；fc′—混凝土塑性有效抗压强度，MPa；ft′—混凝土塑性有效抗拉强度，MPa；fc、ft—混凝土轴心抗压和轴心抗拉强度，MPa；vc、vt—混凝土强度fc、ft的折减系数。α—包络线外法线与竖轴的夹角，推导可得：

(5)

σn=(1-Kcot2α)ft′

(6)

τnt=2Kcotαft′

(7)

破坏机构如图2所示。

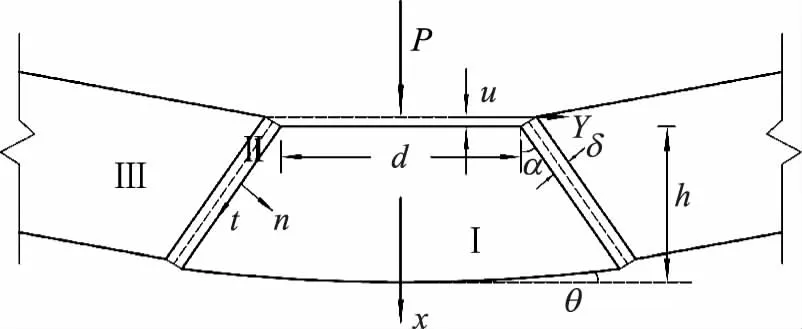
图2 破坏机构

图2中，Ⅰ、Ⅲ为板柱冲切破坏后形成的刚性体，Ⅱ为塑性变形区；d—冲切锥体上表面的宽度，mm；与柱头的宽度一致；n、t—锥体母线的法线方向和切线方向；h—板的厚度，mm。假设塑性变形只发生在塑性区，且冲切锥体只发生竖向的虚位移u。

设塑性变形区的厚度为δ(m)，当冲切体发生竖向虚位移为u时，混凝土塑性区的应变为：

(8)

(9)

由虚功原理可得混凝土部分做的内虚功为：

(10)

式中，A—塑性变形区的表面积，mm2。

将式(6)—(9)带入式(10)，得：

(11)

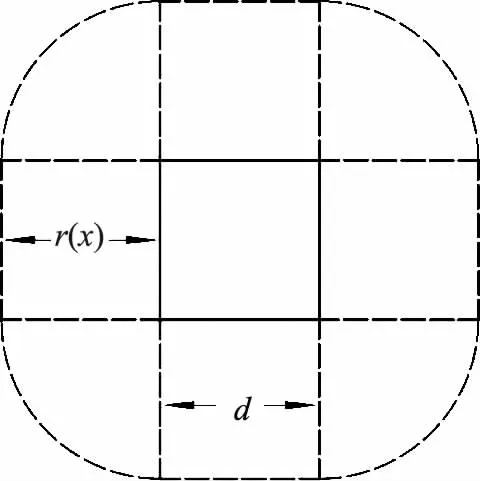
图3 冲切锥体底面形状图

(12)

积分得：

Wc=ft′u(1+Kcot2α)tanα(4dh+πtanαh2)

(13)

1.2 抗弯钢筋提供的承载力

1.2.1销栓作用

当冲切破坏的裂缝穿过钢筋时，钢筋能像插销一样提供剪力，延缓裂缝的发展，增强混凝土板的承载能力，即为钢筋的销栓作用。当板柱发生纯弯曲破坏时，纵筋完全屈服，钢筋不能提供销栓作用力。而试验证明，板柱发生冲切破坏时钢筋并不会完全屈服，此时钢筋能够提供销栓作用[7]。参照文献[8]提出的抗冲切销栓作用的计算式为：

(14)

(15)

式中，φs—穿过破坏截面的抗弯纵筋直径，mm；fc′—混凝土圆柱体抗压强度，MPa；fy—抗弯钢筋屈服强度，MPa；ζ=σs/fy，其中σs为钢筋轴向拉应力，MPa。

当混凝土板双向配筋率相同时，可得：

(16)

式中，As—穿过破坏截面的纵筋截面面积，mm2。

当冲切破坏发生时，破坏截面处钢筋平均应变约为屈服应变的63%，在此取ζ为0.8[9]。当As=(4d+2πh0tanα)h0ρ时，式(15)可简化为：

(17)

式中，ρ—纵筋配筋率；h0—板的有效高度，mm。

1.2.2钢筋拉力

板的受冲切承载力随配筋率的提高而提高。纵筋配筋率的增加，间接加大了受压区的高度，改变了板的内力状态，使板柱冲切承载力提高。而GB 50010—2010则没有考虑配筋的影响。试验表明，当纵筋配筋率高于2.5%时，承载力的提升就不再明显[10-11]，故通常以2.5%的配筋率为界限考虑抗弯纵筋的作用。为便于计算分析，假设钢筋与混凝土之间粘结良好，忽略钢筋与混凝土之间的相对滑移，则钢筋的拉力做功Wst为：

Wst=fyεsAsδ

(18)

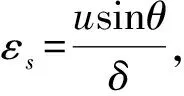
Wst=ufyρ(4d+2πh0tanα)h0sinθ

(19)

将式(13)、(17)、(19)带入式(1)得：

P=ft′(1+Kcot2α)tanα(4dh+πtanαh2)+

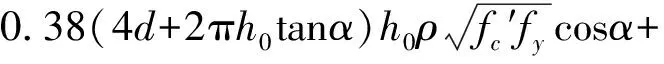
fyρ(4d+2πh0tanα)h0sinθ

(20)

P=0.190fc(dh+1.360h2)+

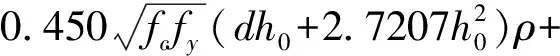
(21)

式中，第一项为混凝土部分提供的承载力，第二项为钢筋销栓作用提供的承载力，第三项为钢筋拉应力提供的承载力。

2 结果对比与修正

2.1 试验值与理论值的对比

收集试验数据总计181组(数据库详情见附录：https://github.com/ohner/data.git)，将试验值与计算理论值进行对比。当配筋率高于2.5%时，配筋率对承载力的提升已不再明显，故为保证计算结果的准确性，舍弃了部分配筋率高于2.5%的试验数据。将所取试验中的混凝土抗压强度进行换算，取美标圆柱体混凝土标准件强度fc′与中标混凝土标准件强度fcu换算关系为fc′=0.8fcu[16]，取混凝土单轴抗压强度fc与150mm混凝土立方体标准件抗压强度fcu换算关系为fc=0.8fcu[17]。计算后得到，预测值与试验值之比的平均值为1.29，变异系数为0.3，由式(21)得到的计算值与试验值的对比图如图4所示。

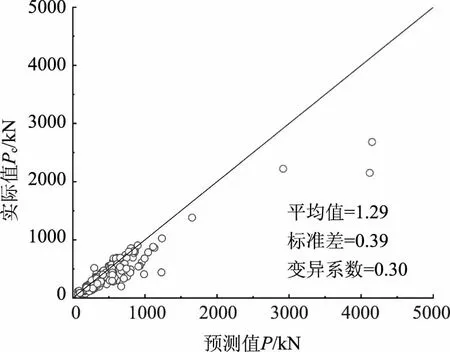
图4 未修正承载力预测值与试验值对比图

2.2 公式修正与对比

为使得计算值更加准确，对式(21)进行参数修正，假定修正后的承载力表达式为：

P=k10.190fc(dh+1.360h2)+

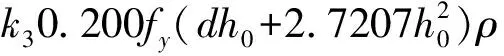
(22)

式中，k1、k2、k3—待定系数。

使用最小二乘法对k1、k2、k3回归分析，使得k1、k2、k3取某个值时计算值与试验值误差最小。

计算得到，当k1=0.356，k2=2.079，k3=2.398时，计算值与试验值最为接近。可以得到修正后的公式为：

P=0.068fc(dh+1.360h2)+

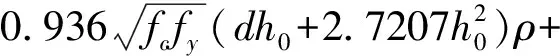
(23)

式中，P(N)—冲切承载力；fc—混凝如抗压强度，MPa；fy—钢筋屈服强度，MPa；ρ—钢筋配筋率；d—柱边长，mm；h—板的厚度，mm；h0—板的有效厚度，mm。

由式(23)得出的抗冲切承载力的计算值与试验值的对比如图5所示，计算得到预测值与试验值之比的平均值为0.92，变异系数为0.20，结果吻合较好，有一定的强度储备。

图5 修正后承载力预测值与试验值对比图

引用GB 50010—2010、欧洲规范Eurocode 2—03[18]、美国规范ACI 318M—11[19]、日本规范JSCE15[20]计算得到的对比图如图6所示。将不同公式预测结果进行对比结果见表1。可以得到，4种规范的预测结果均偏于保守，本文公式获得的结果与实际值最为接近。GB 50010—2010与美国规范ACI 318—11计算得到的结果与实际值较为接近，欧洲规范Eurocode 2—03与日本规范JSCE15计算结果误差较大。