基于经管类专业的极限概念教学设计
2022-07-16郭元春陈思源冀永强
郭元春 陈思源 冀永强

摘 要:极限是微积分学的核心概念,是研究经济管理问题的有力工具。本文结合工程实际,深入挖掘极限理论蕴含着的思政元素,从概念的引入、性质的理解以及一些重要结论等方面进行了分析和探讨。通过这些教学设计,既能帮助学生理解抽象的概念和性质,又能培养学生坚持真理、实事求是的科学态度。
关键词:极限;经管类;无穷小;无穷大;Koch曲线
中图分类号:G4 文献标识码:A doi:10.19311/j.cnki.16723198.2022.17.096
0 引言
2016年12月,习近平总书记在全国高校思想政治工作会议上指出,要坚持把立德树人作为中心环节,把思想政治工作贯穿教育教学全过程。要用好课堂教学这个主渠道,各门课程都要守好自己的一段渠,种好自己的责任田,使各类课程与思政课同向同行,形成协同效应。2020年5月, 教育部颁发的《高等学校课程思政建设指导纲要》指出,理学、工学类专业课程要在课程教学中把马克思主义立场观点方法的教育与科学精神的培养结合起来,提高学生正确认识问题、分析问题和解决问题的能力。理学类专业课程,要注重科学思维方法的训练和科学伦理的教育,培养学生探索未知、追求真理、勇攀科学高峰的责任感和使命感。
《高等数学》是普通高校经管类专业的专业必修课,具有高度的抽象性、严谨的逻辑性以及应用的广泛性。本课程的授课对象主要是大学一年级的新生。学生的特点是对新的环境具有新鲜感,有挑战自我的欲望,但是人生观和价值观还没有定型,缺乏一定的毅力和耐性,也会存在对新环境不适应和迷茫等问题。通过优化教学设计过程,充分挖掘课程中蕴含的思政元素,寻找恰当的切入点把高校思想政治教育融入课堂教学中, 在教学过程中,注重适时引导教育,把价值观引领和人生观的塑造贯穿于教育教学的全过程,培养德智体美劳全面发展的社会主义建设者和接班人。
1 教学设计
极限是微积分学的核心概念,是研究经济管理问题的有力工具。经济学中的边际、弹性以及复利等概念都涉及到极限的思想。在教学设计中,要深入挖掘这些案例中的思政元素,寻找数学知识与德育内容的衔接点,一方面可以帮助学生理解抽象的数学理论和建立数学思维,另一方面也能引导学生挖掘数学美,培养创新思维以及坚持真理、实事求是的科学态度。
1 “问题导入,激发兴趣”的教学设计
极限的概念可以通过割圆术引入。学生通过割圆术的动态演示,理解圆的内接正多边形的面积和圆的面积的关系,自然可以在头脑中形成极限的概念的雏形。学生体会到求极限问题是个动态的过程。在教学过程中,以“润物细无声”的方式,传递我国数学家刘徽的卓越成就,激发学生的文化自信和爱国情怀。
极限概念中,无穷小量和无穷大量是两个非常重要的基本概念。初学者容易在理解无穷小和无穷大的运算性质上有误区。在教学设计中,可以设置如下三个问题:
(1)有限个无穷小的代数和是无穷小,那么无限个无穷小的和还是无穷小吗?
(2)无穷大和无穷大的和还是无穷大吗?
(3)无穷大和无穷大的差是无穷小吗?
对于问题(1),老师给定数列xn=1n,让学生验证。显然,
在n→∞时,xn=1n→0,所以上述极限是无穷多个无穷小的求和问题。通过这个答案可以得到:无限个无穷小的和不一定是无穷小。
这个结果说明要用发展的眼光来看待的事情,不能因循守旧,墨守成规。也能直观地让学生体会有限到无限,量变到质变的过程,让学生明白积少成多,厚积薄发的人生哲理。
对于问题(2),老师给定数列xn=n,yn=-n,让学生验证,显然,
在n→∞时,xn=n→∞,yn=-n→∞,但limn→∞xn+yn=0,即无穷大和无穷大的和不一定是无穷大。
在理解无穷大的概念时,一定要注意无穷大是指绝对值无限增大的量,有正无穷大和负无穷大之分。二者同属无穷大,但是在数轴上看是兩个极端,求和时会出现相抵的情形。
对于问题(3),老师给定数列xn=n2,yn=n,二者同为正无穷,让学生验证,显然,
在n→∞时,xn=n2→∞,yn=n→∞,但limn→∞xn-yn=∞,即无穷大和无穷大的差不一定是无穷小。 这个结果也印证了学海无涯的道理,提醒学生做人,做事要谦虚,要有勇攀高峰的坚韧品格。
借助这个例子,引出无穷大的阶的概念。 让学生领会在自变量趋于无穷大时,基本初等函数中的幂函数,指数函数以及对数函数之间阶的不同。
极限概念的产生,经历了千年的历史,从直觉地感受到描述性定义,再到精确性定义,实际上是一个从特殊到一般,从直观到抽象的过程,引导学生做人做事要有耐心,要有坚持不懈的专注精神。
2 “探究未知,挑战自我”的教学设计
在掌握极限的概念之后,提出教学任务:让学生探究Koch曲线的周长和面积。
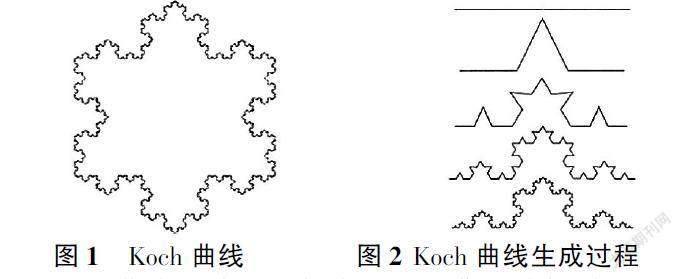
Koch曲线是分形几何中的一个典型范例,如图1所示。 Koch曲线可由一个正三角形生成,即将正三角形的每一边三等分后将中间一段向外凸起成一个以该段长度为边长的正三角形(去掉底边),然后对每一段直线又再重复上述过程(图2所示),这样无休止地重复下去即得Koch曲线。
设初始的正三角形的边长为a,周长为l0,面积为s0,第k次分形后的周长为lk,面积为sk。通过观察图2的变化过程,让学生分析计算得到第一次、第二次分形后的边数、周长和面积,再通过归纳总结,可以得到k次分形后的结果,如表1。
随着分形次数k的无限增加,Koch曲线的周长lk会无限增大,而Koch曲线的面积sk会无限趋于85s0。也就是说Koch曲线的周长无限,面积有限。这个结果与矩形、三角形、梯形、平行四边形、圆等基本图形的结论不一致,会引发学生对于未知知识的渴望,也会让学生意识到学习新知识的时候要基于旧知识,但是也不能完全照搬照抄,要突破常规。
对于Koch曲线周长和面积这个问题,整个探究学习过程经历了从观察、猜想、归纳的过程,通过在数学教学中对学生的严谨性和逻辑性的要求,逐步培养学生坚持真理,一丝不苟,实事求是的科学态度。本题的结论也会启发学生的思维,激发学生的学习兴趣。
3 “环环紧扣,夯实基础”的教学设计
极限的概念和性质可以帮我们准确的理解极限的本质,极限的计算对微积分的核心概念都有重要的作用。熟练地掌握极限的运算技巧可以后续知识的学习做好充足的准备。
极限的计算中,无穷小的等价替换原理也是一个常用的计算方法。该方法在替换的时候只能在乘除因子中进行,如
limx→01-cos2xxsinx=limx→0122x2x2=2
是正确的,但是
limx→0x-sinxx3=limx→0x-xx3=0
就是错误的。错误的源头还是对等价无穷小的概念理解不到位,因此必须在讲等价无穷小的概念时做足准备。由limx→0sinxx=1,limx→0x-x2x=1可以得到:当x→0时,sinx及x-x2均与x等价,显然等价不是等于,二者本质上是不同的。等价的两个无穷小直接差的是一个比其自身高阶的无穷小量, x-sinxx3的分子x-sinx是较x高阶的无穷小,而不能认为是0。
在学习极限的四则运算法则时,会讲到∞∞未定型的极限,如:
limx→∞a0xn+a1xn-1+…+anb0xm+b1xm-1+…+bn
一般的技巧是分子、分母同时除以分子分母的最高次幂。把无穷大通过导数运算化为无穷小,从而得到
limx→∞a0xn+a1xn-1+…+anb0xm+b1xm-1+…+bn=0,n<ma0b0,n=m∞,n>m
实际上,当x→∞时, xn-1的阶比xn的阶要小,即当x→∞时,a1xn-1+…+ana0xn,
所以在计算这个分式的极限时,分子中a1xn-1+…+an,分母中b1xm-1+…+bn的部分可以忽略,从而这个极限本质上计算的就是limx→∞a0xnb0xm。让学生通过无穷大的阶来记忆,可以直接口算得出答案。由于这个方法是将无穷大的最高阶留下来,而其他低阶的部分全部忽略,所以形象地称为抓大头公式。这个公式也可以借助处理问题抓主要矛盾,引导学生重温毛主席的经典著作《矛盾论》,从而将数学思想与哲学原理联系起来,转化为他们的日常思维习惯。
在计算1∞未定型的某些题目时,熟练地应用抓大头公式可以快速地解决计算问题。比如求极限limx→∞x2+1x2-1x,利用抓大头公式,可以确定该极限为1
SymboleB@未定型,可以利用第二个重要极限计算,不难得到
limx→∞x2+1x2-1x=limx→∞1+2x2-1x=limx→∞1+2x2-1x2-122xx2-1
再次对指数部分利用抓大头公式,得到limx→∞2xx2-1=0,从而原极限等于1。这个题属于第二个重要极限的例题,但是这个题目用到了前面说到的抓大头公式,知识点之间的关联很紧密。
通过这些实例,要提醒学生高等数学的知识点都不是独立的,知识点之间都有着联系,所以学习时一定要踏踏实实,夯实基础,切忌好高骛远,碎片化学习。
3 结束语
理学课程要在课程教学中一方面要提高学生正确认识问题、分析问题和解决问题的能力,另一方面要注重科学思维方法的训练和科学伦理的教育,培养学生探索未知、追求真理、勇攀科学高峰的责任感和使命感。在进行教学设计时,从多个角度深入分析课程思政建设内容,将课程的教学过程转化为对学生进行价值引额的有效载体,在讲授知识、培养能力的同时塑造学生的品德和价值观,从而实现“知识传授、能力培养与价值引领”相融合的教学目标,最终提高学生的综合素养。
参考文献
[1]习近平.习近平在全国高校思想政治工作会议上强调:把思想政治工作贯穿教育教学全过程开创我国高等教育事业发展新局面[N].人民日报,20161209.
[2]教育部高教司.高等学校课程思政建设指导纲要[Z].教高[2020]3号.
[3]吴素琴,王鹏,王振纬. 基于课程思政建设的重要极限教学设计[J].高等数学研究,2021,(8):125127.
[4]郑奕.大学数学“课程思政”的思考与实践[J].宁波教育学院学报,2019,21(1):5961.
[5]高中喜,王轉德,谢云荪.课程思政在高等数学教学中的探索和实践[J].高等数学研究,2021,24(4):9395,98.
[6]葛喜芳,朱兴旺.《高等数学》课程思政的单元数学设计——以《导数的概念》为例[J].现代商贸工业,2021,(30):115116.
[7]同济大学数学系.高等数学(第七版)[M].2014.
