基于失效边数概率分布的K-终端网络重要度计算方法

杜永军, 惠树鹏, 蔡志强, 孟学煜

(1.兰州理工大学 经济管理学院,甘肃 兰州 730050; 2.西北工业大学 机电学院,陕西 西安 710072)

0 引言

K-终端网络(简称为网络)是现代通信网络、交通网络等网络系统的抽象数学模型，其是由节点和边组成的抽象图，其中一些不可分割的关键节点组成了终端集合K。例如，在通信网络中，节点可表示交换机，而边可表示电缆。假设节点绝对可靠而边会以一定的概率发生失效，K-终端网络的可靠性定义为K中任意两个终端都被一些运行的边连通的概率[1]。

网络可靠性分析的一个重要目标是识别网络薄弱环节以及量化网络的边对网络可靠性的影响力。为此，重要度的概念被提出和研究，并被广泛应用于网络可靠性优化设计和维修决策。给定二态关联系统，自从学者Birnbaum于1969年首次提出重要度分析方法以来，国内外许多学者在系统可靠性和风险分析领域，从不同的角度提出了不同的重要度以量化组件对系统可靠性的影响力，包括Fussell-Vesely 重要度，可靠性完成值，可靠性减少值，Barlow-Proschan 重要度，Natvig重要度，以及它们的推广[2～5]。Zhu等人[6]研究了线形连续n中选k系统的基于Birnbaum重要度的系统组件的排序模式，并分析了该排序模式关于组件可靠性和组件总数的变化机理。崔利荣等人[7]引进了带有一定稀疏度的连续系统，并利用有限马尔可夫链嵌入方法建立了该系统的可靠性以及组件的Birnbaum重要度的方程。Hsu和Yuang[8]提出了“两阶段”算法来评估网络边的Birnbaum重要度。Page和Perry[9]定义了网络的一条边的“收缩-删除”重要度，并利用一种基于图论技术的分解算法来评估该重要度的值。但是，对于一般的网络，其可靠性和重要度的计算均为NP-难问题，因此Gertsbakh等人[1,10]设计了基于组合计数技术的蒙特卡洛(Monte-Carlo，MC)算法，以近似评估网络边的Fussell-Vesely重要度和Birnbaum重要度。

以上重要度从不同角度量化边可靠性和边本身占据的位置对整个网络可靠性的影响程度，其在K-终端网络可靠性优化和维修决策方面发挥了巨大的作用。但这些网络重要度的计算方法存在一定的局限性，如依赖于边的可靠性，且需要边发生失效相互独立的条件。对于一些实际应用的网络，一方面只存在有限的失效数据，使得难以通过数理统计的方法而得到边的可靠性的值；另一方面由于级联失效的原因，导致边的失效失去独立性。这些事实极大的限制了网络重要度计算方法的应用范围，使得不能满足对一些现实网络开展重要度分析的需求。

在工程实践中，当网络处于运行或失效状态时，其发生失效的边的数目为一随机变量，且该随机变量应该满足一定的概率分布，这就急需开展基于该概率分布的网络可靠性建模和重要度计算方法的研究。因此，面向以上网络重要度评估的需求，为了突破传统网络重要度计算需已知网络边的可靠性，且边发生失效相互独立的条件限制，本文在给定失效边数的概率分布的背景下，构建网络可靠性模型，并据此推导出网络重要度的计算方法。

1 K-终端网络可靠性建模

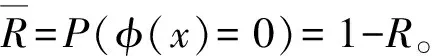
网络中的谱在网络可靠性和重要度研究中发挥着重要的作用，它分为D-谱和C-谱。令随机变量X表示网络中发生失效的边的总数目，从网络失效的角度，可定义网络的D-谱为F(k)=P(φ=0│X=k)，而边i的D-谱是F(k,0i)=P(φ=0,xi=0│X=k)，以及F(k,1i)=P(φ=0,xi=1│X=k)，k=1,2,…,n。这些D-谱的概率意义可作如下解释：当给定恰好k条边发生失效时，F(k)是网络发生失效的概率；F(k,0i)是网络和边i都发生失效的概率；F(k,1i)是网络失效且边i运行的概率；注意F(k)=F(k,0i)+F(k,1i)。

相似的，从网络运行的角度可定义网络C-谱是：F′(k)=P(φ=1│X=n-k)，而边i的C-谱是：F′(k,1i) =P(φ=1,xi=1│X=n-k)和F′(k,0i)=P(φ=1,xi=0│X=n-k)。这些C-谱的概率意义解释如下：当给定网络中恰好有k条边运行(即n-k条边恰好发生失效)时，F′(k)是网络运行的概率；F′(k,1i)是网络和边i均运行的概率；F′(k,0i)是网络运行且边i失效的概率。同时需注意F′(k)=F′(k,1i)+F′(k,0i)。

需要指出的是，本文假设网络中所有的边失效同分布，故D-谱和C-谱的数量值仅依赖网络结构，故又称为网络结构不变量[1]。在网络所有全部边失效同分布的背景下，根据组合计数原理，可得P(xi=0│X=k)=k/n。注意，网络全部边失效时，即X=k=n，边i必然发生失效，即P(xi=0│X=n)=n/n=1；当全部边运行时，即X=k=0，边i必运行，即P(xi=0│X=0)=0/n=0。因此，利用全概率公式，可得边i的失效概率的方程:

(1)

结合全概率公式和网络中的D-谱的定义，可得到下列三个概率方程。

网络的失效概率方程：

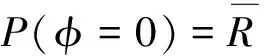
(2)

网络和边i均失效的概率方程可写作：

P(φ=0,xi=0)

(3)

此外，网络失效且边i运行的概率方程可写作：

P(φ=0,xi=1)

(4)

同理，当网络全部边失效同分布时，根据组合计数原理可得到P(xi=1│X=k)=(n-k)/n，再结合全概率公式，边i的可靠性方程可写作:

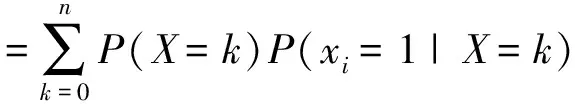
(5)

另外，网络可靠性方程可写作：

P(φ=1)

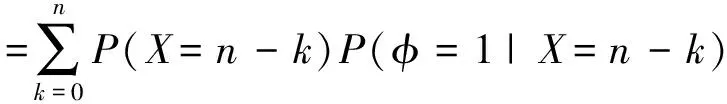
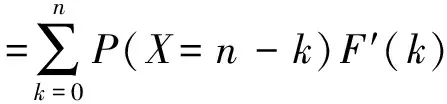
(6)

上面方程(6)的第一个等式是由全概率公式得到，而第二个等式由网络C-谱的定义得到。同理，网络和边i均运行的概率方程可写作如下：

P(φ=1,xi=1)

(7)

网络运行且边i失效的概率方程可写作：

P(φ=1,xi=0)

(8)

2 K-终端网络重要度计算方法

贝叶斯重要度：面向二态关联系统，当系统发生失效时，工程师感兴趣的是究竟哪一个组件引起的系统失效，以及不同的组件对系统失效的贡献度。为此目的，Birnbaum给出了系统组件贝叶斯重要度。当系统失效时，定义一个组件的贝叶斯重要度为这个组件失效的概率，它的数学表达式是：BAYi=P(xi=0│φ(x)=0)。

面向K-终端网络，当给定发生失效的边数的概率分布时，边i的贝叶斯重要度方程BAYi可写作：

BAYi=P(xi=0|φ=0)

(9)

Birnbaum重要度：给定一个二态关联系统，定义组件i的Birnbaum要度如下：由这个组件i状态的变化而引起的系统失效概率的改变量，即Ii=P(φ=0│xi=0)-P(φ=0│xi=1)。给定K-终端网络，基于条件概率公式，结合方程(1)，(3)，(4)和(5)，则边i的Birnbaum重要度Ii可写作:

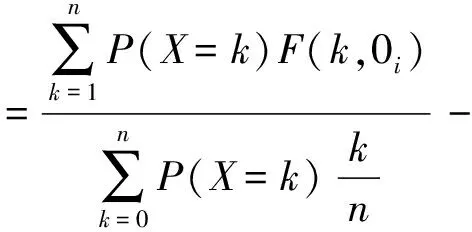
(10)

临界可靠性重要度：当一个二态关联系统处于运行状态时，Kuo和Zuo[11]定义了一个组件i的临界可靠性重要度CSi为这个组件运行且对系统运行致命的概率，其中致命的含义是：当该组件运行时，则该系统运行；当该组件失效时，则该系统失效。一个组件i的临界可靠性重要度CSi的数学方程可写作:

(P(φ=1|xi=1)-P(φ=1|xi=0))

(11)

当给定K-终端网络发生失效的边数的概率分布时，根据条件概率公式，再将方程(1)，(5)，(6)，(7)和(8)代入方程(11)，则得到边i的临界可靠性重要度CSi:

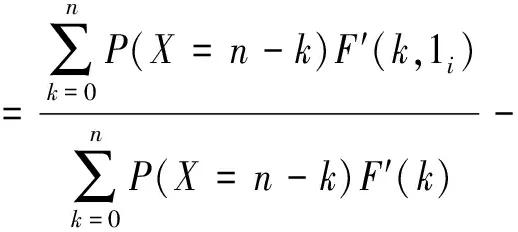
(12)

临界失效重要度：给定一个二态关联系统，当该系统处于失效的状态时，Kuo和Zuo[11]定义了一个组件i的临界失效重要度CFi，其是该组件失效且对系统失效致命的概率，依据条件概率公式，整理CFi如下:

(13)

在给定K-终端网络发生失效的边数的概率分布的背景下，将方程(1)，(2)，(3)，(4)和(5)代入方程(13)，则可得边i的临界失效重要度:

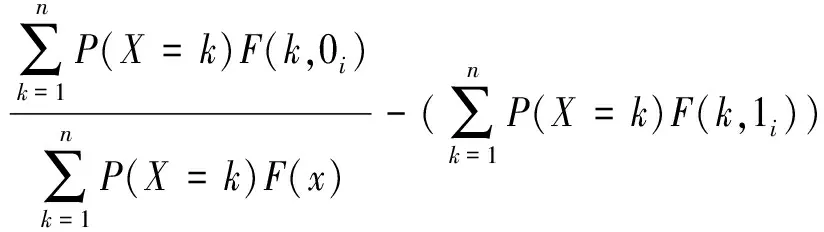
(14)

可靠性减少值：面向二态关联系统，在组件i失效的背景下，Levitin给出了“可靠性减少值”的重要度RRWi，它量化了系统可靠性的潜在损坏程度，其数学方程为:

(15)

在给定K-终端网络发生失效的边数的概率分布的背景下，将方程(1)，(6)，(8)，代入方程(15)，则得到:

(16)

可靠性完成值： 面向二态关联系统，Vasseur等学者定义了一个组件i的可靠性完成值RAWi，其量化了由于这个组件i的运行而引起的整个系统可靠性增加的百分比，它的数学方程可写作:

(17)

面向K-终端网络，当给定网络发生失效的边数目的概率分布时，依据条件概率公式，整理方程(17)，并将方程(5)，(6)，(7)，代入后，则得到RAWi的数学方程：

(18)

3 算例仿真

给定图1所示网络，其是由30条边组成的十二面体网络，该网络可用于刻画计算机网络的拓扑结构，其运行当且仅当终端1和20被一些运行的边连通，假设节点完全可靠而边以共同的概率发生失效，且失效边数的总数目服从参数为λ的饱和泊松分布，其概率质量函数可写作:

(19)

需要指出的是，由于发生失效的边数最大值为30(该十二面体网络总计只有30条边)，故该泊松分布在k=30时发生饱和，称为饱和泊松分布，其可用于模拟电网中发生失效的电线数目的概率分布。

首先利用以色列学者Gertsbakh等人[1,10]设计的Monte-Carlo仿真方法得到十二面体网络的D-谱和C-谱的近似值，以此为基础，再结合该网络发生失效的边数的概率质量函数(19)，利用方程(9)，(10)，(12)，(14)，(16)，(18)，分别评估该十二面体网络的贝叶斯重要度BAY，Birnbaum重要度I，临界可靠性重要度CS，临界失效重要度CF，可靠性减少值RRW，以及可靠性完成值RAW。当分布中的参数λ取较小的值(λ=1)时，取中间的值(λ=15)时，取较大值(λ=40)时，表1，2，3分别报道了根据这些重要度进行排名的前10名的网络边和相应的重要度的值。

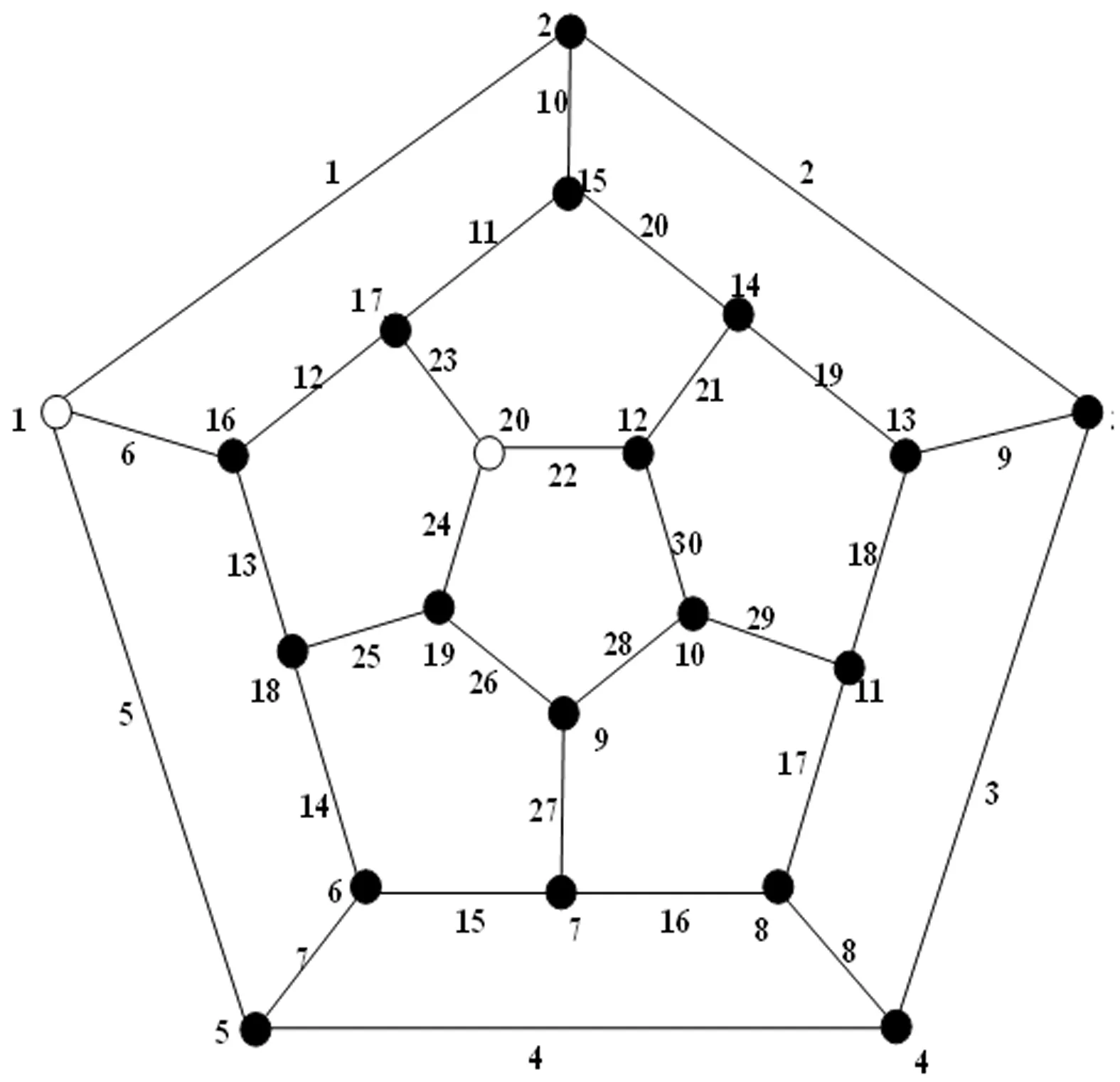
图1 十二面体网络K={1,20}

观察表1，2，3可知，基于同一个重要度，当λ取不同值时，则得到不同的网络边排序。例如，基于贝叶斯重要度BAY，当λ=1时，边6，1，5，22，23，24为网络中最重要的6条边；但是，当λ=40时，边6，12，23是网络中最重要的3条边。此外，注意观察图1可知，至少需3条边发生失效，才能导致终端节点{1，20}失去连通性，具体的，边1，5，和6发生失效，或者边22，23，24发生失效。注意这些边恰为λ=1时，基于贝叶斯重要度BAY识别出的最重要的6条边；相反，要确保终端节点{1，20}保持连通性，至少需3条边维持运行状态，即边6，12，23，而这恰为λ=40时，贝叶斯重要度BAY识别出的最重要的3条边。

根据表1，2，3可知，当我们固定λ的值时，重要度BAY，I，CS，CF分别导出了相同的排序，而重要度RRW和RAW则分别导出了另外一种相同的排序。注意表1，当λ=1时，前四种重要度导出了最重要的10条边均为6，1，5，22，23，24，12，11，7，13；而后两种重要度均导出了最重要的10条边为27，20，5，10，2，4，11，6，30，23。

注意在表1中，当λ取较小值时(λ=1)，对于前4种重要度而言，基于同一重要度，不同网络边的重要度值的差异非常显著。例如，基于贝叶斯重要度BAY，排名第1的边6和排名第10的边13的重要度值分别为0.51518和0.05508 ，这一重要度值的差异非常显著的事实，使得很容易区别哪一条边更重要。

但在表1中，对于后两种重要度而言，给定某一重要度时，不同边的重要度的值非常接近。例如，基于可靠性减少值RRW，排名第1的边27与排名第10的边23的重要度的值分别为0.36969和0.36880，这两个值非常接近，再考虑到MC方法数值误差的影响，以致发现基于可靠性减少值RRW，难以区别哪一条边更重要。

与上述结果相反，当λ取较大值时(λ=40), 观察表3可知，就前4种重要度而言，基于同一重要度，不同边的重要度值比较接近。尤其基于贝叶斯重要度BAY，排名第1的边23和排名第10的边11，其数值非常接近，分别为0.99603和0.99597，以致于很难区分哪一条边更重要。

但在表3中，对于后两种重要度而言，不同网络边的同一重要度的值的差异非常明显，如基于可靠性减少值RRW，排名第1的边23和排名第10的边22，其值差异明显，分别为6.32280和1.22449，据此，很容易区分哪一条更重要。

当λ取中间值时(λ=15)，由表2可知，除排名第4到排名第7的边之间排序稍有差异外，根据这6种重要度，均导出了相同的排序，但要注意各个重要度的物理意义不同。例如，尽管贝叶斯重要度BAY和可靠性完成值RAW均识别出边10为第8条重要的边，但叶斯重要度BAY告诉我们：当该十二面体网络发生失效时，边10失效的概率为0.56651；而可靠性完成值RAW则告诉我们：当我们确定边10处于运行状态时，则得到十二面体网络可靠性为原十二面体网络可靠性的1.22279倍。

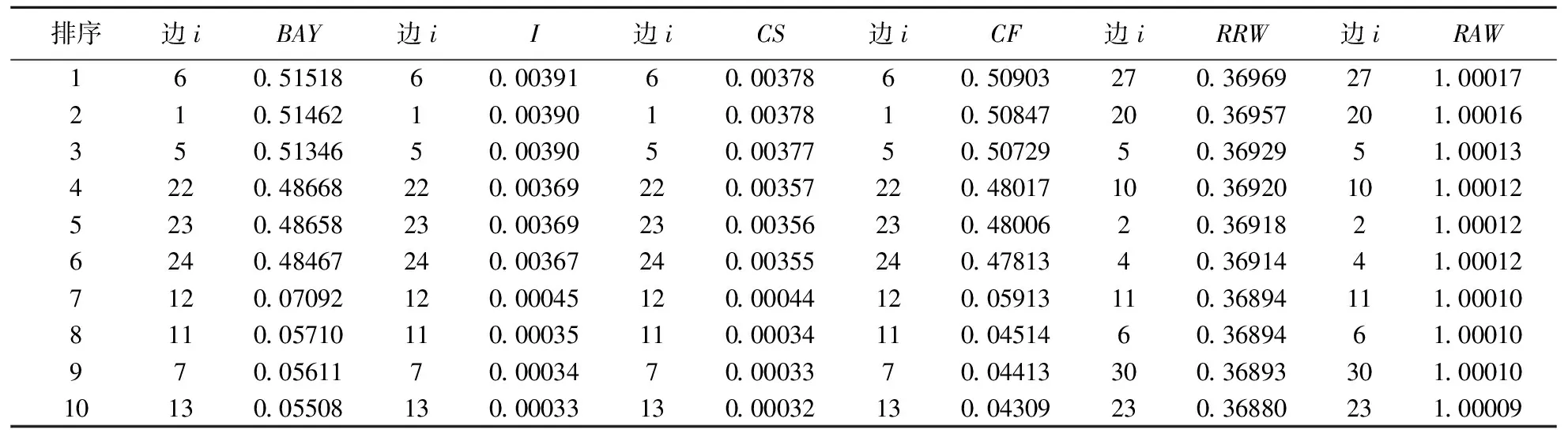
表1 参数λ=1的各个重要度值及排序

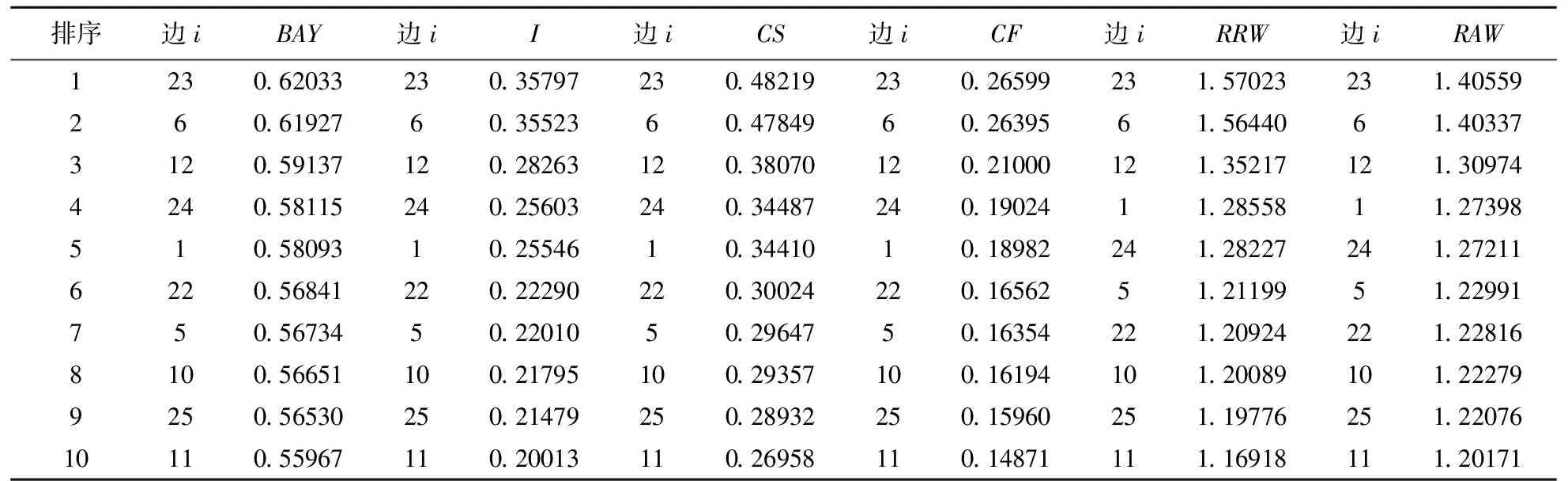
表2 参数λ=15的各个重要度值及排序

表3 参数λ=40的各个重要度值及排序

4 结论

本文在给定K-终端网络发生失效的边数的概率分布的背景下，构建了K-终端网络可靠性模型，导出了K-终端网络边的贝叶斯重要度、Birnbaum 重要度、临界失效重要度、临界可靠性重要度、可靠性完成值、可靠性减少值等重要度的数学方程。本文研究结果突破了以往K-终端网络可靠性和重要度计算方法均依赖于边的可靠性且需边失效相互独立的条件的限制，其丰富了网络可靠性和重要度的理论体系，并为网络可靠性优化和维修决策奠定了基础。以后的研究将继续着眼于在给定网络发生失效的边数的概率分布的背景下，探讨两条边的联合重要度的计算问题，阐释概率分布中的参数对联合重要度的影响机理，为网络薄弱环节的精确识别提供新的思路。