基于自适应无迹卡尔曼滤波的四旋翼无人机姿态解算

刘康安， 张伟伟， 肖永超， 叶 沐

(1.上海工程技术大学，上海 201000； 2.清华大学，北京 100000)

0 引言

无人机的姿态估计是其稳定飞行的基础，姿态解算的精度直接关系到姿态控制的稳定性。近年来，随着微机电系统(MEMS) 技术的快速发展，低成本、低功耗、体积小的MEMS惯性传感器广泛应用于四旋翼小型无人机的姿态解算[1]。其中，具有优越静态特性的加速度计在静止状态下有较高的测量精度，具有良好动态响应特性的陀螺仪在短时间运动状态下有较高的测量精度，具有长时间测试稳定性的磁力计容易受到周围环境中的外部扰动磁源的干扰，但陀螺仪不受磁场源的干扰[2]。所以，使用单一的传感器解算姿态角往往精度较低，难以满足平稳飞行的要求。而采用多传感器数据融合的方法获得更加精确的姿态输出是当前无人机领域的研究难点和热点。

目前常用的航向和姿态信息融合算法有互补滤波(Complementary Filter，CF)[3]、卡尔曼滤波(Kalman Filter,KF)和梯度下降法[4]等。其中，互补滤波算法相对容易实现，计算成本低。然而，其输出的姿态和导航的精度略低于卡尔曼滤波估计的精度，其高、低通滤波器转接频率难以确定，在动态环境中测量精度较差。LEFFERTS等[5]使用卡尔曼滤波算法进行姿态信息融合，建模简单、滤波速度快，但其只适用于线性高斯噪声系统，忽略了非线性因素给滤波带来的影响。针对多旋翼飞行器等非线性系统，文献[6]提出一种基于扩展卡尔曼滤波(Extended Kalman Filter，EKF)算法的飞行器姿态信息融合方法，但在姿态确定过程中，系统方程的线性化步骤采用雅可比矩阵更新状态转移矩阵和观测矩阵，稳定性差、估计偏差大。面对EKF算法存在的问题，文献[7-9]提出使用无迹卡尔曼滤波(Unscented Kalman Filter，UKF)算法进行无人机姿态解算，减小了EKF算法线性化带来的误差，且无需计算雅可比矩阵，具有更快的收敛速度。在UKF算法中，基于无迹变换生成的sigma-point近似值更新方程[10]，凭借其更高的姿态求解精度和强鲁棒性，尤其适合于高度非线性运动学模型的姿态估计。然而，根据经验选择的UKF算法关键参数——过程噪声协方差Q对复杂工作环境下的估计精度有很大影响。文献[11]通过求解系统误差协方差之间的比率对过程噪声协方差矩阵进行在线调整。

综合考虑姿态解算精度、计算速度和算法实时性的需求，提出一种优化的自适应无迹卡尔曼滤波(Adaptive Unscented Kalman Filter，AUKF)算法。采用梯度下降算法对过程噪声协方差Q进行调优，梯度下降算法具有全局收敛速度快、运算速度快、实现简单等优点，可以用来调整过程噪声协方差Q，提高UKF算法的姿态解算精度和性能。

1 无人机姿态建模

1.1 建立坐标系

无人机姿态测量需要建立符合右手定则的2个坐标系和3个姿态角，分别是导航坐标系、机体坐标系、偏航角(ψ)、横滚角(φ)和俯仰角(θ)。导航坐标系n是相对大地水平面定义的正交坐标，坐标轴Xn,Yn,Zn分别指向地理上的北、 东、地方向。机体坐标系b固定在无人机上，坐标轴Xb,Yb,Zb分别指向无人机的前方、右侧以及底部。导航坐标系到机体坐标系的坐标变换矩阵可由式(1)的方向余弦矩阵表示，即

(1)

1.2 系统模型建立

借助四元数法表述航向和姿态变化的过程因具有无奇点以及计算量小等优点而被广泛应用。刘兴川等[12]提出了一种基于四元数的MARG传感器姿态测量算法，实现三自由度的姿态测量，显著提高姿态测量精度。本文选用四元数进行姿态解算，将陀螺仪得到的数据进行四元数更新后得到的值当作预测值，观测值为加速度计和磁力计的测量值。

1.2.1 基于加速度计的姿态估计

加速度计输出的是载体的加速度，用加速度计计算姿态角时，坐标系n下的重力加速度为gn=(00g)T，加速度计在坐标系b下的输出为ab=(axayaz)T，其转换关系可以表示为

(2)

通过上式得到的加速度，可以得出基于加速度计的俯仰角和横滚角分别为

(3)

1.2.2 基于磁力计的姿态估计

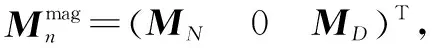
(4)

因此，地磁矢量在水平方向上的分量为

(5)

则偏航角可表示为

(6)

ψmagn=ψm+α

(7)

式中，α为磁偏角。

1.2.3 基于陀螺仪的姿态估计

陀螺仪输出的是敏感载波角加速度。基于四元数的陀螺仪角速度动态模型更新可表示为

(8)

则式(8)的矩阵形式为

(9)

采用四元数微分方程的皮卡逐次逼近法对式(9)求解，其离散形式为

(10)

用四元数表示从机体坐标系到导航坐标系的坐标变换矩阵可写作

(11)

因此，无人机姿态角可以用四元数形式表示为

(12)

2 基于自适应无迹卡尔曼滤波器的姿态解算

在本章中，提出一种优化的自适应无迹卡尔曼滤波器来解算无人机的姿态角。为了提高算法的性能，采用梯度下降算法对无迹卡尔曼滤波器的关键参数进行了调整，即过程噪声协方差Q。图1给出了基于梯度下降算法优化的自适应无迹卡尔曼滤波(AUKF)姿态估计的全过程。

图1 基于AUKF的姿态解算流程图Fig.1 Flow chart of attitude calculation based on AUKF

2.1 梯度下降算法

作为求解无约束优化问题的常用方法，梯度下降算法具有实现简单的优点。梯度下降法的基本思想是选择一个合适的初值x(0),迭代更新x的值，最小化目标函数直到收敛。梯度下降的输入是目标函数f(x)，梯度函数g(x)=▽f(x)和计算精度ε;输出是f(x)的最小值x*。梯度下降的过程可以详细总结如下。

1) 初始关键参数x(0)和k。

2) 计算目标函数f(x(k))。

4) 设变量x(k+1)=x(k)+λkpk，更新函数f(x(k+1))。如果||f(x(k+1))-f(x(k))||<ε或||x(k+1)-x(k)||<ε，停止迭代，并让x*=x(k)。否则，令k=k+1，然后回到步骤3)去寻找另一个更优的最小值。

5) 当目标函数为凸函数时，梯度下降的解为全局最优解。

2.2 传统UKF设计

2.2.1 状态方程

状态预测是基于之前的最优估计，且无迹卡尔曼滤波器的离散时间非线性动态状态方程为

xk=Ak-1xk-1+ωk-1

(13)

式中:xk和xk-1分别为时刻k的先验估计和时刻k-1的后验估计;ωk是协方差Q的过程噪声，简化为独立高斯白噪声。Ak是状态转移矩阵，可以得到

(14)

2.2.2 量测方程

校正状态是细化测量估计的关键步骤。量测方程表示为

zk=H(xk)+vk

(15)

式中:vk是具有噪声协方差R的独立高斯测量噪声，Hk(xk)为输出函数，其算式为

(16)

2.2.3 无迹变换

计算2n+1个sigma点，即

(17)

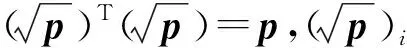
计算sigma点对应的权值,即

(18)

2.3 过程噪声协方差

由于无人机与周围环境的耦合作用，在无人机飞行和悬停过程中，机体会产生随机振动和加速度，导致过程噪声协方差Q难以确定。

(19)

(20)

2.4 基于梯度下降的无迹卡尔曼滤波

基于卡尔曼线性滤波框架的UKF不是传统的线性化非线性函数的方法，而是利用无迹变换传播均值和协方差。与扩展卡尔曼滤波相比，无需推导雅可比矩阵的UKF可以使状态变量近似于非线性函数的概率密度分布，具有更强的鲁棒性和精确性。但过程噪声协方差Q在一定程度上影响滤波性能，可以采用梯度下降法对无迹卡尔曼滤波进行改进。基于梯度下降算法优化的无迹卡尔曼滤波流程如下。

(21)

式中，i=0,2，…，2n。

2) 根据步骤1)得到的sigma点，通过式(13)状态方程计算系统状态变量的预测值和协方差矩阵为

(22)

3) 对步骤2)的预测值再次进行UT变换，计算出新的sigma点，即

(23)

式中，i=0,2，…，2n。

4) 根据步骤3)得到的新sigma点，通过式(15)中的观测值计算出观测变量的预测值和协方差矩阵可

表示为

(24)

式中,i=0,2，…，2n。

5) 无迹卡尔曼滤波增益矩阵为

(25)

6) 无迹卡尔曼滤波系统的状态更新和协方差更新算式为

(26)

(27)

式中:L(·)为损失函数；RMSE(·)为估计结果的均方根误差函数；x′为姿态估计系统的真状态值。

3 实验验证

为了验证本文所提AUKF算法的精确性和有效性，搭建了基于pixhawk的飞行实验平台并在室外进行无人机动态飞行实验。然后，将实验结果与LPMS-IG1P高精度惯性测量单元读取的数据进行对比，验证了所设计系统的优异性能和实用性。本文设计的姿态测量系统由MPU9250三轴陀螺仪，MPU9250三轴加速度计和LSM3030C三轴磁力计组成，选用STM32MP157作为微处理器，通过I2C总线与上位机进行通信。

实验设置采样频率为10 Hz，选取连续60 s内的姿态测量数据，图2(a)、图3(a)和图4(a)为实验过程中高精度惯导读取的实际横滚角、俯仰角以及偏航角。本文分别采用常规卡尔曼滤波(KF)、无迹卡尔曼滤波(UKF)和本文所提的自适应无迹卡尔曼滤波(AUKF)算法进行姿态解算，并将3种算法解算出的横滚角、俯仰角和偏航角数据与实际角度进行对比，得到如图2(b)、图3(b)和图4(b)所示的3种算法的估计误差。本文采用均方根误差(RMSE)来评估算法的估计精度，3种算法的均方根误差对比见表1。

图2 横滚角姿态变化及测量误差Fig.2 Attitude variation and measurement error of roll angle

图3 俯仰角姿态变化及测量误差Fig.3 Attitude variation and measurement error of pitch angle

图4 偏航角姿态变化及测量误差Fig.4 Attitude variation and measurement error of yaw angle

表1 3种算法的均方根误差Table 1 RMSE of three algorithms (°)

从图2～4中可以看出，基于常规卡尔曼滤波算法的姿态解算误差最大，横滚角最大误差为2.1°，俯仰角最大误差为2.5°，偏航角最大误差为3.8°。与常规卡尔曼滤波算法相比，无迹卡尔曼滤波算法姿态解算精度更高，其横滚角最大误差为1.4°，俯仰角最大误差为1.6°，偏航角最大误差为2.9°，但由于噪声协方差Q被设定为经验值，导致其估计误差仍然较大。而本文提出的自适应无迹卡尔曼滤波算法通过梯度下降来调整Q，大大提高了UKF的估计性能，因此其姿态解算效果最好，估计误差明显小于UKF和KF算法，横滚角和俯仰角最大误差分别小于1.1°和1.3°，偏航角最大误差优于2.2°。表1给出了动态飞行实验中3种算法获得的俯仰角、横滚角和偏航角的均方根误差，本文算法获得的3种姿态角的均方根误差最小，UKF算法的均方根误差略大于本文算法，KF算法的均方根误差最大。综合来看，本文算法具有更好的滤波效果，满足无人机姿态解算的实用性要求。

4 结束语

针对四旋翼无人机姿态解算问题，本文提出了一种优化自适应无迹卡尔曼滤波的姿态解算算法。该算法采用梯度下降算法对过程噪声协方差进行在线调整，优化状态预测估计，有效降低了姿态解算的误差。在姿态建模中以四元数作为状态量，消除了Euler角的奇异问题，同时减少了运算量。为了验证所提算法的姿态解算精度，做了室外飞行实验并进行了分析和比较。实验分析结果表明，本文算法与KF和传统的UKF算法相比具有较高的精度，在动态飞行环境下横滚角和俯仰角均方根误差小于0.5°，具有一定的工程应用价值。