拓扑优化在提高一体化框架模态特性中的应用
2022-07-15于淼楼宇涛
于淼,楼宇涛
(中国电子科技集团公司第二十七研究所,郑州 450047)
0 引言
作为重要承载部件,一体化框架为各单机提供稳定、可靠的机械支承环境,必须具备一定的刚度和强度,在承受加工、装配、运输、装卸、试验所产生的各种载荷后,仍能保持结构稳定性,满足精度要求。如果一体化框架在工作过程中出现变形或者断裂,将严重影响产品的精度、稳定性。
拓扑优化是结构优化设计领域最常用的方法,是结构优化的一种常见形式。在产品设计阶段,灵活运用各种拓扑优化技术,可以确定结构材料的最佳分配方案,以便对结构形式进行改进设计,不但节约了生产成本,同时还实现了产品经济、高效的设计。在方案阶段研制过程中,对一体化框架结构进行拓扑优化设计,既要满足多种工况下的强度、刚度要求,又要保证一体化框架质量达到最优,进而控制一体化框架的质量,实现提高一阶模态的目的。一体化框架的结构如图1 所示,内部为正八边形筒体,以轴线为中心呈几何对称分布,主要由上法兰、下法兰和纵梁组成。
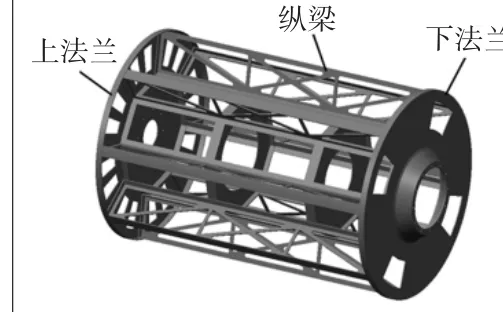
图1 一体化框架三维模型
1 拓扑优化理论
随着科学技术的不断向前推进,结构拓扑优化是目前结构优化过程中重要的设计手段[1],结构拓扑优化方法也在不断发展,我国在拓扑优化领域已做了大量研究。拓扑优化在结构设计中处于概念设计阶段,它是一切后续设计的基础。目前连续体的拓扑优化方法主要有均匀变化法、变密度法、渐进结构优化法及水平集方法。变密度法是连续体拓扑优化常用的方法。
在优化的过程中,每一个单元对应一个优化变量值,通过不断的优化迭代,结构材料分布理想状态时1阶模态频率达到最大值。结构材料尽可能分布均匀,使连续变量的拓扑优化模型能更好地逼近离散变量。每个单元的相对密度和材料的弹性模量之间存在某种相对应的关系,通过变量连续取值,优化计算后,单元密度大的区域应当保留,该区域的材料应该重点关注;单元密度小的区域则可以去除,该区域的材料为冗余材料,因此实现了材料的高效率利用,实现了拓扑优化设计[2]。
为了提高一体化框架八面体筒形结构的模态特性,把1阶频率最大作为目标函数,在优化迭代的过程中,根据结构材料分布情况,当1阶频率达到最大时,模态频率和振型也发生变化,通过不断地迭代优化实现迭代过程中的收敛性和稳定性[3]。
2 有限元模型建立及模态分析
2.1 有限元模型建立
一体化框架为柱状八边形结构,包络尺寸为φ1162 mm×1692 mm。各零部件采用螺装拼接的结构形式,材料选用7075铝合金,弹性模量为71 GPa,泊松比为0.3,密度为2810 kg/m3,屈服极限为505 MPa,质量为92.7 kg。
网格划分有限元分析中很重要的一步,直接影响计算结果收敛性。好的网格会更逼近结果,本文采用六面体网格划分和自由网格划分相结合的方法,对优化区进行多区域体网格划分,网格划分速度快,节约内存和计算时间,在优化区域和接触位置进行网格加密,从而提高网格质量[4]。
2.2 模态计算结果
模态分析主要可以反映结构的动态特性,主要表现为结构的固有频率及振型。一体化框架八面体筒形结构约束条件为两端面固支,即上、下法兰面约束。模态分析结果如表1所示,前三阶模态振型如图3所示。

表1 一体化框架前三阶模态频率

图2 一体化框架有限元模型
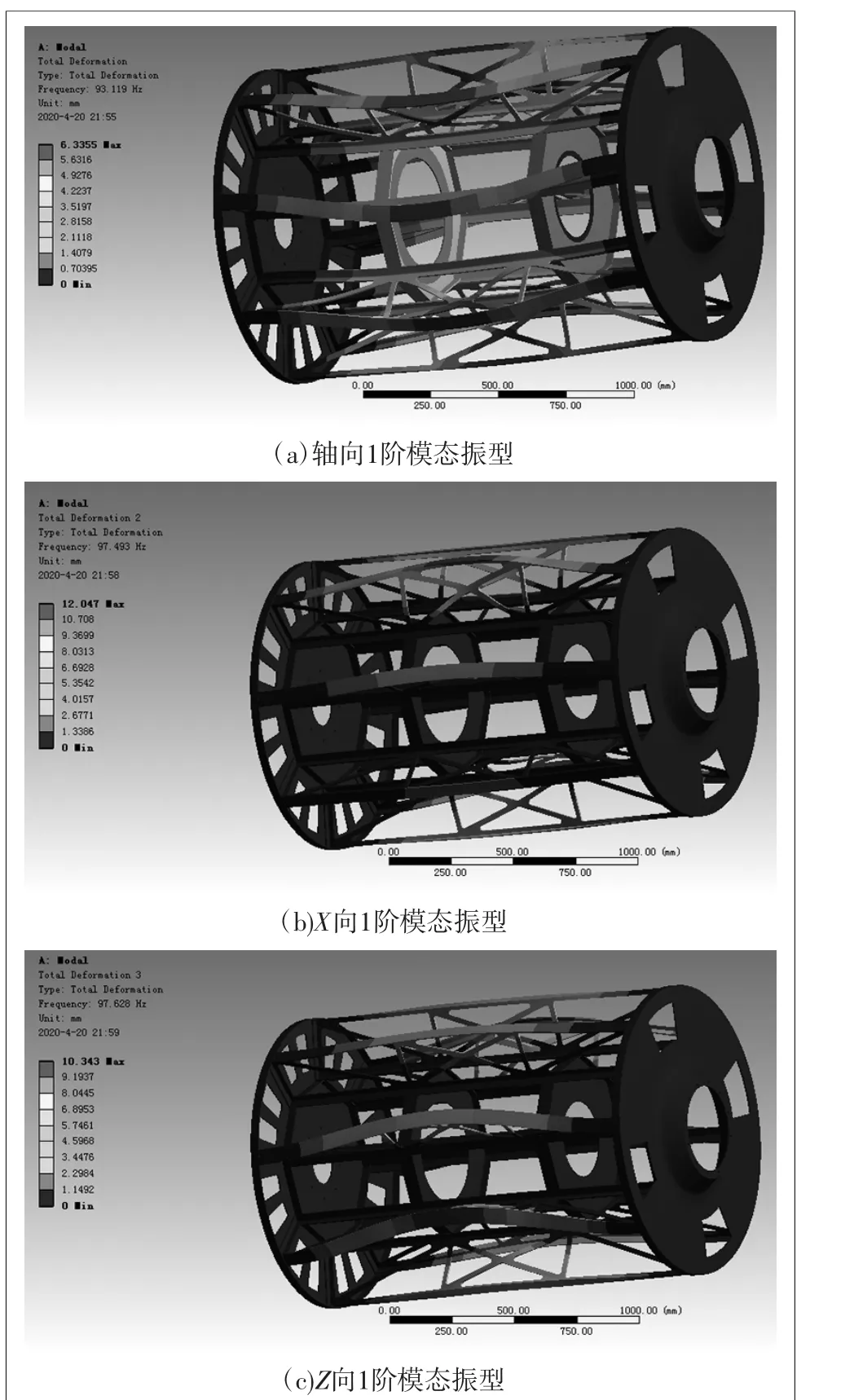
图3 一体化框架1~3阶模态振型
固支状态下,轴向1阶扭转大于93.119 Hz,X、Z 向均大于97 Hz,未达到基频大于100 Hz的指标要求。由于1阶频率接近工作频率,可能会引起共振,主要表现为扭转,对系统的破坏程度很大,从而影响一体化框架使用寿命和安装精度,所以有必要对一体化框架的1阶频率进行改进以提高其性能。
3 一体化框架拓扑优化方案
整个框架以8根纵梁作为主支承结构,周向均匀分布,8根纵梁两端面与上、下法兰螺装成一体。为改善一体化框架的模态特性,以一体化框架的一阶模态频率最大化为目标,对其内部零部件重新进行结构设计,基于计算结果进行一体化框架轻量化二次设计,去除了多余材料并加强结构的薄弱部分。优化对象分为纵梁、上法兰和下法兰[5]。
3.1 纵梁优化方案
考虑纵梁与上、下法兰端螺栓孔固定的工况下,纵梁结构的传力路径不太清晰,将纵梁的设计域对基频进行拓扑优化,设计域显示如图4、图5所示。

图4 初始设计

图5 纵梁设计域
根据结构的传力路径,对纵梁中的连接结构进行结构优化,参数化模型建立流程如下。
1)考虑到梁板内侧固定的支撑盘,这里认为连接梁下端应该与下面支撑盘对齐较为合理,所以连接梁的下端坐标保持在此处不变,对上端的连接处与左端距离作为参数x进行控制。2)考虑一体化安装结构在轨状态为两端同时固定,使得两个固定端都分布8根连接梁,初始基频为78.129 Hz,最优解按照基频排序列表如图7所示,其中基频为96.657 Hz的最优解对应梁板结构如图8所示。

图6 连接梁内侧端固定
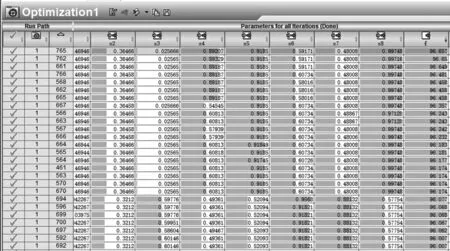
图7 基频排序

图8 纵梁基频最优结构
3.2 上、下法兰优化方案
考虑在前后法兰螺栓孔固定的工况下,将前后法兰作为设计域对基频进行拓扑优化,设计域显示如图9、图10所示。

图9 上法兰设计域

图10 下法兰设计域
首先将体分比设置为30%进行拓扑优化,在第50次迭代结束,得到的优化收敛列表(如图11),左边为目标函数基频,右边为设计域剩余体积比例,拓扑结果如图12~图13所示。

图11 优化列表1

图12 上法兰优化结果1

图13 下法兰优化结果1
接下来将体分比设置为60%进行拓扑优化,在第68次迭代结束,得到的优化收敛列表和拓扑结果如图14~图16所示。
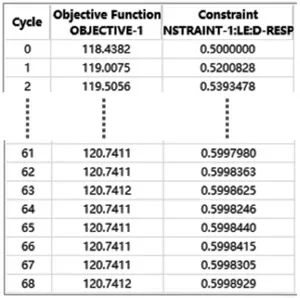
图14 优化列表2

图15 上法兰优化结果2

图16 下法兰优化结果2
下法兰因为设计域中保留了原有的连接所需的孔洞,所以拓扑结果不太均匀。对比两次拓扑优化的结果可以看到,虽然剩余体分比有很大差别,但材料分布是存在一些共性规律的,另一方面分析优化列表可以看到,两次不同体分比下基频结果相差不大并且在优化过程中基频并没有很大提升,可以看出上下法兰的设计域内的材料分布对基频并没有太大影响,因此在后面设计过程中将主要依据较小体分比的那个拓扑结果来进行,如图17、图18所示。

图17 前端框设计
3.3 优化结果分析
采取拓扑优化措施后的一体化框架进行模态分析,其前三阶模态计算结果如表2所示,各阶固有模态频率振型如图19所示。经过优化改进后的一体化框架与初始结构相比,一阶模态频率为118.95 Hz,质量为88.5 kg(优化前为92.7 kg)。满足设计指标要求。

表2 改进后的一体化框架前3阶模态频率
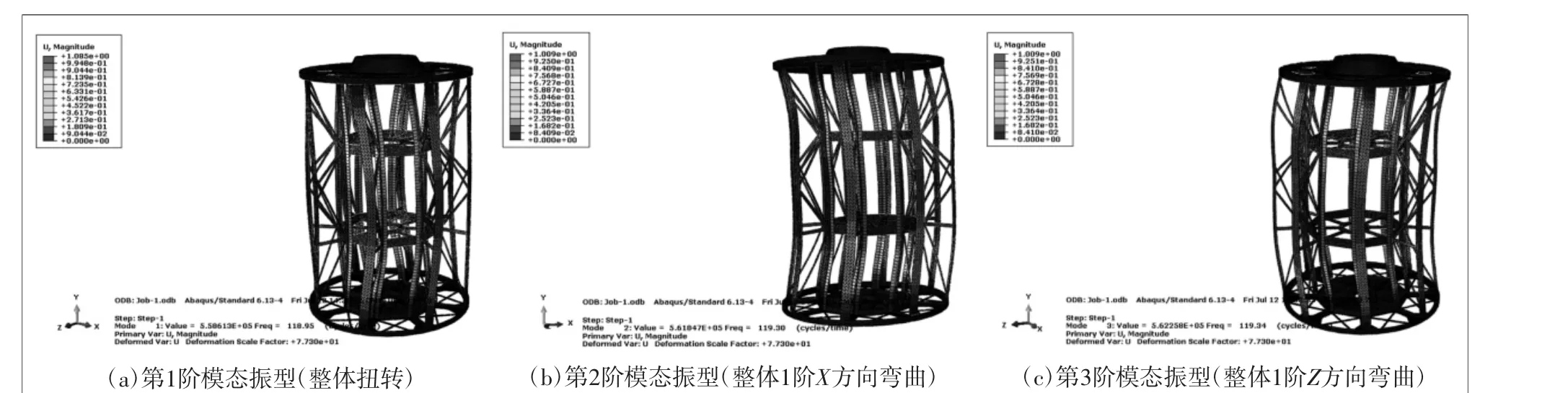
图19 优化后的1~3阶模态振型
4 结语
本文运用拓扑优化原理,对一体化框架制定了轻量化设计方案,并对优化结果进行模态分析,一体化框架的1阶频率从93.119 Hz提高到118.95 Hz,改善幅度达27.7%,质量减少了9%,既提高了一体化框架的模态特性,又节约了材料成本,对于一体化框架改进设计具有一定的参考价值。
