基于满意度函数和灰关联度的多公差约束配准算法*
2022-07-15陆正新梁永收楚亚松任军学
陆正新,梁永收,楚亚松,任军学
(1.西北工业大学航空发动机高性能制造工业和信息化部重点实验室,西安710072;2.北京动力机械研究所,北京 100074)
随着我国航空航天器性能的不断提高,关键零部件的性能要求也随之不断提高,其显著变化就是零件精度要求越来越高,零件形状更加复杂,复杂曲面类零件应用更加广泛。为降低重量,航空航天器关键零部件多为薄壁件,为提高气动能力多外形采用自由曲面,传统加工工艺对于此类零件多采用大余量毛坯数控切削成形,这种加工方式存在效率低、成品率低以及成本高等不足。随着先进制造理念的不断发展,采用近净成形工艺的复杂曲面类零件在航空航天领域的应用更加广泛,该类零件多采用精密锻造或者精密铸造精确成型,具有强度高、节省原材料等优点。近净成形类零件部分区域精确成形,仅需要对剩余区域进行少量机加工。近净成形类零件精确成形区域虽然成形精度较高,但由于成形工艺等原因仍会产生一定程度的变形,其真实形状与理论模型的偏差不尽相同,且机加区域留有加工余量未精确成形,因此毛坯形状与余量并不确定,该部分测量数据无法准确反映模型的形状,呈现出测量数据缺失的特点[1]。若采用传统加工工艺,直接按照设计的理论模型进行加工,由于成形误差的存在,必然导致加工区域与近净成形区域无法光滑过渡,出现拼接误差,且两者的相对位置关系无法保证,会导致形位公差超差。
自适应加工技术适用于解决加工区域之间有相对位置关系要求以及毛坯余量分布不均匀等问题,是提高近净成形类零件加工精度与加工效率的有效方法,其主要流程如图1所示,首先,根据零件的结构特征规划测量区域与测量路径,根据测量的数据构建工艺坐标系;测量数据经处理后,运用多公差约束配准算法与理论模型进行匹配,获取理论模型加工区域在毛坯中的位置;其次,在零件装夹状态下进行在机测量,根据装夹测量数据以及加工区域位置生成加工程序。模型配准作为近净成形类零件自适应加工的关键技术,其首要功能是建立起零件测量数据坐标系与设计模型坐标系之间的变换关系。其次,配准过程完成了加工可行性分析与位姿优化的任务。
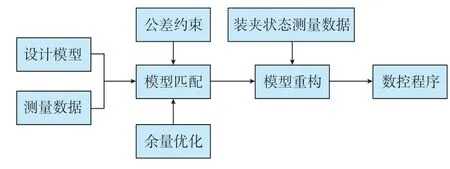
图1 自适应加工流程图Fig.1 Adaptive processing flow diagram
目前关于配准算法的研究多集中于检测基准确定的配准模型或配准评价方法。其中Fan等[2]提出一种采用边界曲线的配准方法,通过对点云测量数据与理论CAD模型的边界进行均匀采样,根据边界曲线点的方向角序列偏差进行匹配,根据匹配结果即可得到点云数据相对CAD模型的旋转角度。Lang等[3]采取SQP算法解决最小区域问题,将最小区域约束分解为非线性规划约束条件,通过条件转化的方式对问题进行求解,其中采取STL形式曲面微分对点到曲面的欧式距离进行了计算。Ma等[4]提出一种基于混合框架与变分推理的三阶段配准策略(TRS)点云配准方法,通过设计一个含有各向同性和各向异性的高斯变分混合模型(GVMM)来减少异常值的影响,并采用Dirichlet分布来控制高斯分量的混合比例用以识别缺陷点。Zhang等[5]使用最小二乘平方和误差作为评价方法,并且关注了匹配过程中对应点重复的解决方法,通过选择次优点防止重复对应带来的误差。Mehrad等[6]研究了不同点集数量在一些约束条件下的置信度,从概率方面对配准精度作出了解释。Bergström 等[7]针对曲面须重复配准的要求,对最近点迭代算法进行了优化改进,其基于KD-tree数据结构提出了距离变化网格树(Distance varying grid tree)的数据结构对理论模型数据进行存储,通过优化存储方式使算法速率得到提升。Mellado等[8]在配准算法方面针对4ps算法提出了改进,使之有更好的运算精度与效率,在交叠数据超过50%的情况,依然有较好的运算性能,在图像处理方面有一定优势。He等[9]提出了GF-ICP算法,此算法运用点云的曲率、曲面法矢、点云密度等几何性质与属性,以避免在对应点集搜索中出现陷入局部搜索的情况。Huan等[10]提出了一种叶片误差评估方法,第1步通过最近点迭代算法使带匹配对象与目标对象贴合,第2步在截面内再次运用ICP算法进行截面内匹配,此时的评价函数为最小二乘平方和,最后一步,分别将叶盆、叶背、前缘、后缘4个区域轮廓度误差的最大正偏差与最大负偏差相减,所得的4个数值求总和,将目标函数修改为该总和最小,通过预配准提高了搜索效率,两步精配准达到了误差评价的目的。Albarelli等[11]采取博弈算法完成了配准过程,此过程无需初始配准,通过权重变化使得高匹配度测量点发挥更大作用,进而提高配准的稳定性。Usamentiaga等[12]对传统ICP配准算法的优缺点进行了详细分析与总结,提出了新的二维平面内的对应点匹配方法,采用主成分分析法确定局部位置的法向,并采用改进的R型树结构存储模型对算法进行加速。Srivatsan等[13]采用SPNR(稀疏点以及法矢配准)方法,在测量点稀疏并且已知测量点法矢的情况下,通过对测量点施加扰动,完成配准,该方法对于测量点的选择较为重要,不同的测量点和不同幅度的扰动可能会带来不同的结果。Myronenko等[14]提出一种全新的配准方法,命名为一致性点漂移,采用两个点云的相似概率密度最大为寻找对应点的条件,以高斯混合模型求出最大的相似概率,该方法可以完成刚性配准与非刚性配准。Combès等[15]提出一种新的三维点集非线性配准方法,该方法将第1个点集视为高斯混合模型,采用期望最大化算法对该模型的参数进行最大后验估计;Zhang等[16]建立了公差约束下的余量优化模型,根据一些特殊要求建立了几种不同模型,可应用于不同余量分布情况的毛坯。詹旭等[17]提出一种基于余弦相似度的配准方法,以两点的余弦相似度为条件,采用差分优化算法求解最优变换参数。
当前研究大多集中在对应点搜索以及算法加速等方面,评价标准多为偏差最小,并未考虑形位公差的约束,因此本研究提出一种基于灰关联度的多公差约束配准算法,采用灰关联理论耦合形位公差,最后采用BFGS迭代算法求解。
多公差约束配准算法的计算流程如图2所示,首先确定参与配准的公差项目,评价各公差的偏差量;然后根据公差对配准结果的影响程度建立满意度模型,并计算各公差的满意度值;再根据计算得到的满意度值计算公差的灰关联度值,得到配准权重分布;接着搜索匹配点,消除敏感对应的点对,最终求解刚性变换参数。
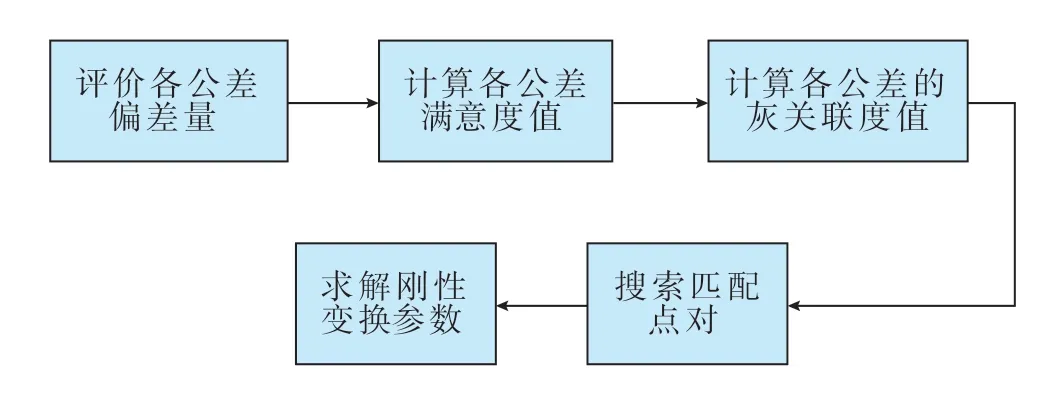
图2 多公差约束配准算法流程图Fig.2 Multiple tolerance constraints registration algorithm flow diagram
1 多公差耦合约束配准模型构建
1.1 形位公差评价方法
位置度是指被测要素的位置相对于基准的变动量,位置度公差区域表示方法为以基准中心为圆心的圆形,如图3所示,或以基准为形心的方形,如图4所示。本研究采用圆形区域进行计算。
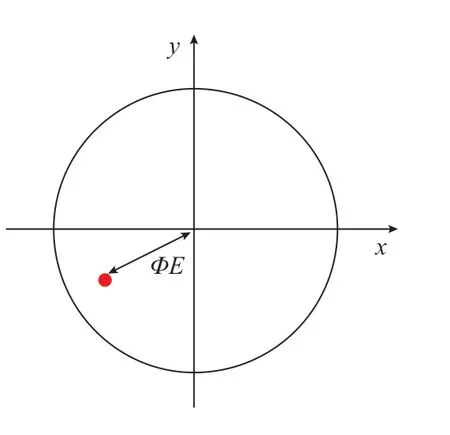
图3 位置度圆形表示方式Fig.3 Circular representation of positional tolerance
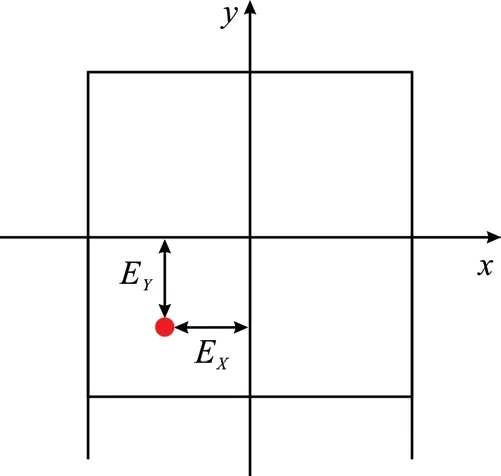
图4 位置度方形表示方式Fig.4 Square representation of positional tolerance
位置度的偏差刻画了实际被测要素中心与基准中心的偏移程度,位置度评价依赖于基准点的位置与基准轴线方向,为简化计算,采用极坐标表示圆位置度偏差,如式(1)和(2)所示。


式中,ρ为位置度圆形条件下的偏差半径;θ为偏差方向与极轴的夹角;x、y为偏差半径向正交坐标轴的投影值;E为计算得到的夹角。
轮廓度用于描述曲面尺寸准确度,其主要指标为轮廓度误差,是指被测实际轮廓相对于理想轮廓的变动情况。
轮廓度的评价前提是对实际评价区域的精确测量,依据测量结果给出测量区域的轮廓度误差,因此,需要根据测量结果找出距离测量区域的最远点,若测量数据为接触式测量设备(三坐标测量机)采集得到,则计算测量点集合P中的元素pi到测量面的最近距离dmin与最远距离dmax,则此时轮廓度误差Tol为最远距离与最近距离之差,如式(3)所示。

1.2 基于满意度函数的公差转化方法
多公差的约束问题可视为多目标的协同优化问题,从而将约束条件转化为求解结果。满意度函数的主要作用是反映各目标的重要程度,为保证其数量级比例,需要将每个目标转化为特定的满意度函数hi,通常为0≤hi≤1。满意度评价方法大体有值越大越好、越小越好以及特定区域内较好等方法,函数形式也多种多样,常见有矩形函数(式(4)、图5)、半阶梯函数以及岭型函数[15]。本研究采用值越小越好的评价方式。
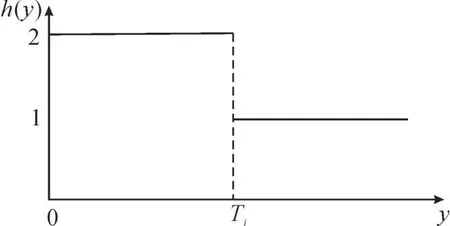
图5 矩形函数Fig.5 Rectangular function
式中,yi为公差偏差量;Ti为参与评价的公差带带宽。
考虑到位置度公差与轮廓度公差在公差容许范围内可以为其他因素判定提供裕度,但超过公差限则成为限制条件,故使用特定区域内的半阶梯与岭型复合函数,如图6和式(5)所示。
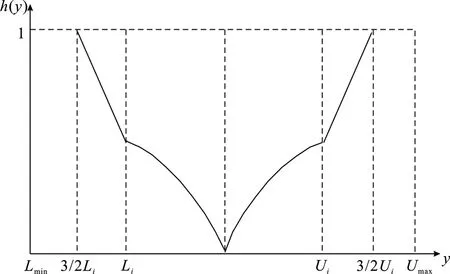
图6 半阶梯、岭型复合函数Fig.6 Half-step, ridge-type composite function
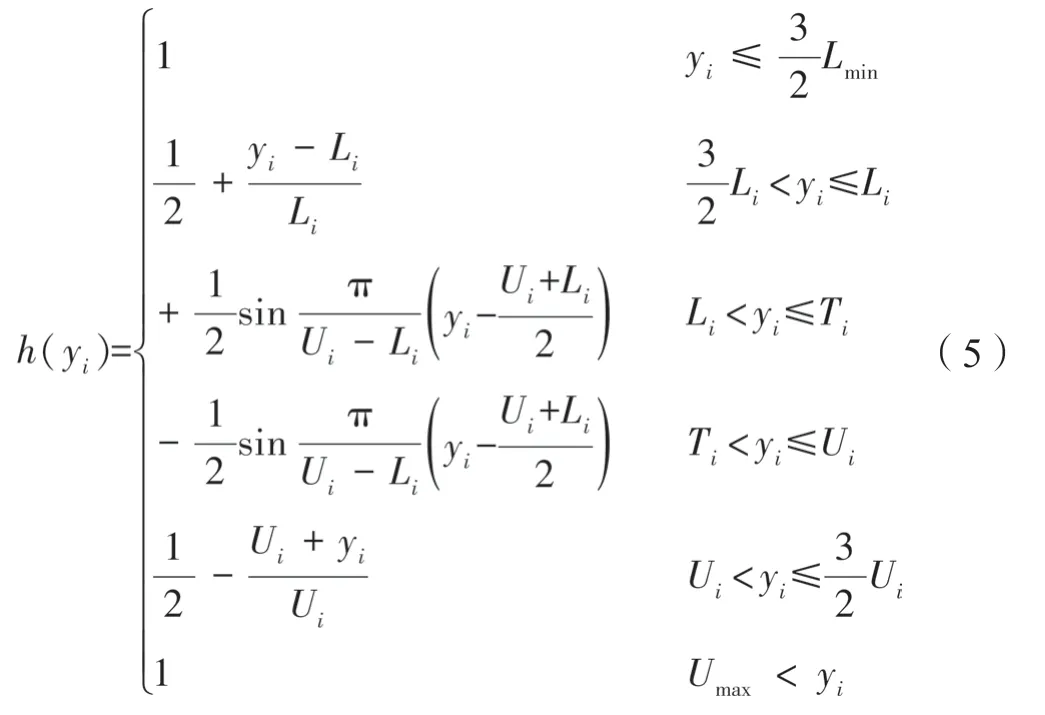
式中,Lmin为函数定义域下限;Umax为函数定义域上限;Li为公差带下限;Ui为公差上限。
总体满意度函数能够有效将多约束优化问题转化为单目标优化问题,通过不同公差间权重的改变来实现公差间的平衡,对于公差权重ω的设定,可以先由设计人员赋予初始权重,再根据实际情况进行修正,修正过程可借助灰关联度方法。因此,本研究采取几何平均法(式(6)),用以避免单个响应局部过优而其他响应过劣的情况。
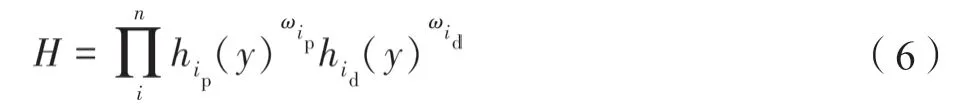
式中,H为各公差耦合后的满意度值;hip为第i个测量点的位置度公差满意度值;ωip为第i个测量点的位置度公差满意度值权重;hid为第i个测量点的轮廓度公差满意度值;ωid为第i个测量点的轮廓度公差满意度值权重。
1.3 基于灰关联度的多公差耦合方法
灰关联度法的基本思想是一个看似复杂的系统内部,同样有一定的规律和联系。将复杂的关系序列化,建立灰关联度模型,此方法以大数据样本为依据,通过轮廓度公差与形位公差偏离程度的横向比较,揭示公差对几何距离偏差的作用机制,从而确定了几何与公差间的协同优化关系。
考虑到物理意义不同因素的量纲可能不统一,无法直接进行比较,通常首先对数据进行处理,实现各参数的无量纲化。本研究的输出参数为单个公差的最大幅值与波动范围,为反映重要程度,二者的理想状态都是越大越好,因此采用“目标越大越好”的方法。式(7)为采用“目标越大越好”的数据归一化处理方法。
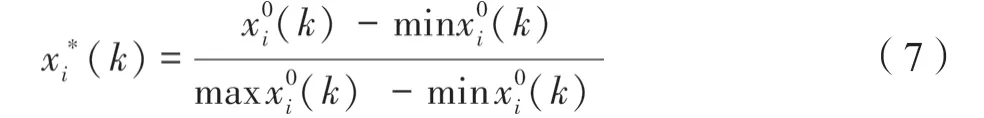
式中,)为数据预处理后的序列(相似性序列);k)为参考序列;max(k)为参考序列中的最大值;min(k)为参考序列中的最小值。
接下来,利用式(8)~(11)来计算灰关联度系数(GRC),从而得到各优化目标与输入参数的关联程度。
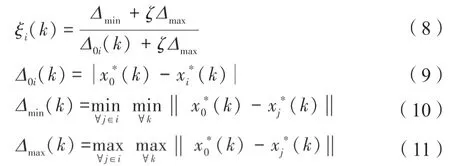
式中,)为序列标准值,依据文献[16],通常为1;(k)为可比性序列;Δ0i(k)为偏差序列;Δmin(k)取0,Δmax(k)取1;ζ为分辨系数,ζ∈[0,1],通常取ζ=0.5。
经计算后可得各公差相应的最优灰关联度值,重新归一化,可得到各系数ωi,计算公式如式(12)所示。

通过式(12)可计算各公差相应的最优灰关联度值,对该值重新进行归一化,可得到各系数,从而建立基于多工差约束的配准模型,如式(13)所示。
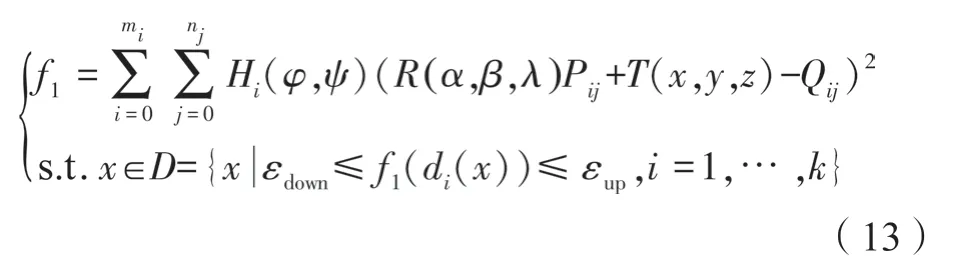
式中,Hi(φ,ψ)为以位置度公差、轮廓度偏差为自变量的满意度函数;f1为近合格零件配准目标函数。
2 多公差约束配准算法求解
配准技术主要由匹配特征、相似度衡量、约束空间、搜索策略4个部分组成,如图7所示。匹配特征是从配准模型中提取出来的用于匹配的信息,即匹配主体;约束空间是指用来校准模型的空间变换集,即约束条件;相似度测量则决定了每一个配准测试的结果,即收敛条件;搜索策略决定如何在搜索空间中选择下一个变换,如何测试并搜索出最优变换,即应用于配准的算法。
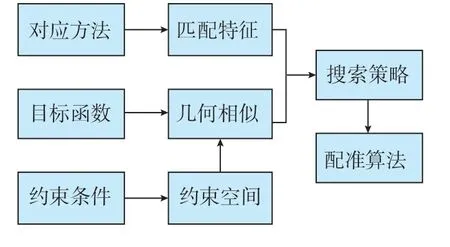
图7 配准技术主要组成部分Fig.7 Main components of registration technology
2.1 对应点搜索策略
匹配问题的实质在于匹配对象间元素的对应,近净成形类零件配准过程是围绕测量数据点云与理论模型展开的,通常将其转化为测量点与曲面上的对应点之间的关系。元素间的对应程度对匹配结果影响较大,由于点对间的关系并非一一对应,可能存在一对多等情况,如图8所示,不均匀的对应关系容易造成匹配区域的局部敏感性,使算法陷入局部收敛或降低运算精度。
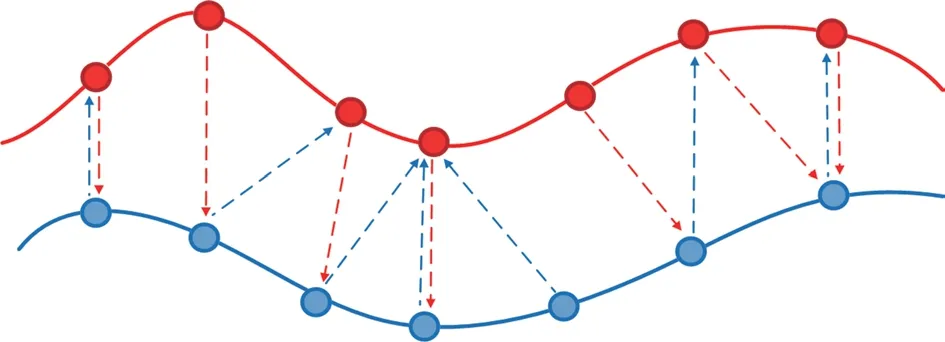
图8 局部敏感对应方式Fig.8 Local sensitive counterpart
现针对此类问题提出改进方法,步骤如下:
(1)将目标曲面进行参数化,得到参数表达形式S(u,v)。
(2)已知测量规划点间距为l,根据距离公式求解测量点Pi(x,y,z) 的最近点Qi(x,y,z),并以Qi(x,y,z)为圆心,kl为半径建立目标球Sphere(x,y,z),其中k为调整系数。
(3)求解其他测量点(x,y,z)的对应点(x,y,z),若Qi'(x,y,z)在目标球内,则以球边缘点作为初始点搜索第2临近点作为(x,y,z)。
(4)重复前3步,至所有测量数据得到理想的对应点。
通过上述方法可得到一一对应点对,如图9所示。
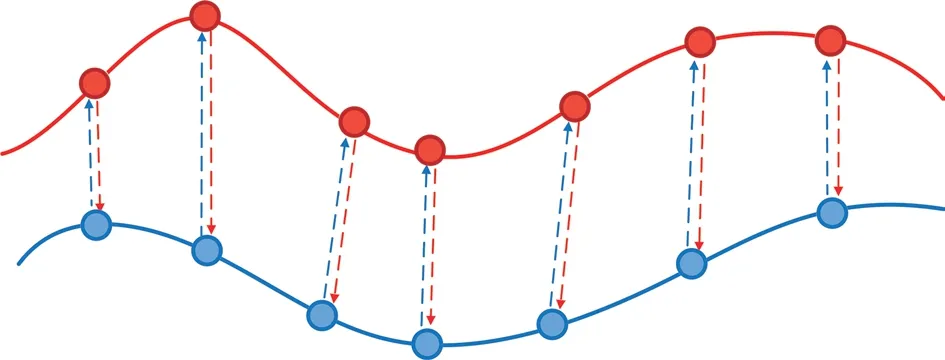
图9 改进的对应方式Fig.9 Improved correspondence method
2.2 近合格类零件配准求解算法
本研究采用带罚函数的目标函数形式,将带约束函数求解问题转化为无约束函数求解问题。由于可行域变换矩阵的非连续性与不直观性,本研究选取外点罚函数法采取后评价策略对该问题进行求解。
首先,将满意度约束值Hi的不等式形式转化为等式约束形式(式(14)),因此可将式(13)改写为增广拉格朗日形式的表达式(式(15)),
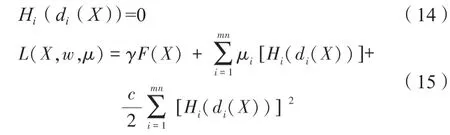
式中,c为惩罚因子;μi为拉格朗日乘子;γ为归一化常量,γ>0;这里所指di(X)为相对曲面的有向距离,代表了曲面方向,di(X)=Di(X)·
式(15)目的在于搜寻L(X,w, μ)的全局最小值,其中wi随符合要求程度提高而降低,因此符合公差要求的测量点数目越多,函数整体值越低。
由w(di(iX))两端点为0与知,分别带入式(16)和(17)。

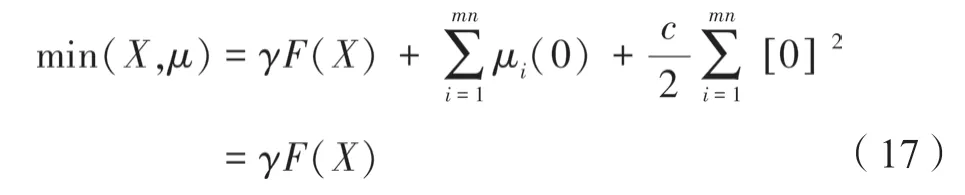
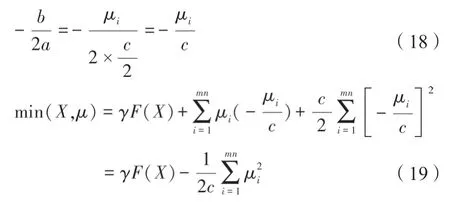
经比较式(19)可合并两端点,合并后为式(20),即完成了迭代形式。
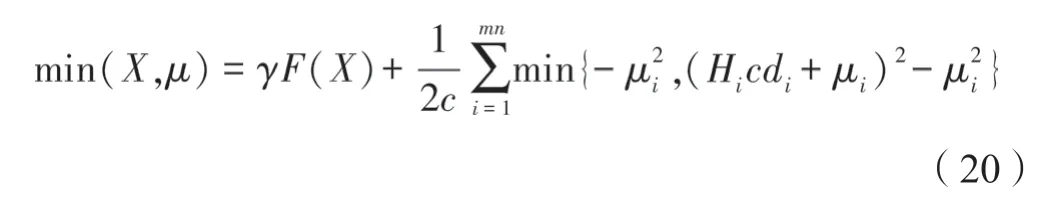
式中,μi表示迭代终止条件,根据式(20),可转换为式(21)。

当求解式收敛时μi无限接近于μi+1,即当|μi+1-μi|<ε时迭代截止。
迭代算法选取BFGS的类海森矩阵求解形式,此算法比较适合在大规模的数值计算中,具备牛顿法收敛速度快的特点,通过海森矩阵的近似替代方式,有效节省了存储空间和计算资源。
3 算法验证
本研究选取某型号转子发动机叶片,该叶片为精锻叶片,即叶身采用精密锻造工艺成型,不需要二次加工,仅需要加工榫齿、前后缘及叶尖部分,是典型的近净成形零件,叶片理论模型与采样截面高度如图10所示。模型按照等参数方式离散初始点,同时为模拟实际叶身型面,按照期望0.03mm,方差0.03mm添加仿真用高斯噪点,测量点共2800个,测头半径1mm,为减少精配准迭代次数与时间,对模拟测量数据进行预变换,使得模拟数据更接近理论叶型,预变换采用四点对应(4PCS)与最近点迭代(ICP)组合算法实现。初始参数见表1。
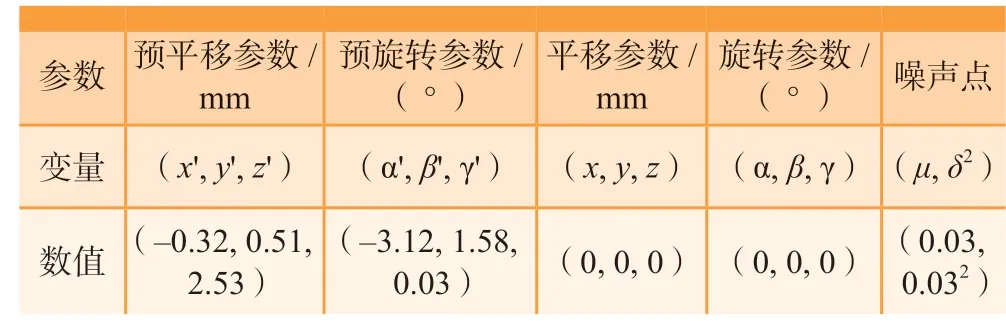
表1 平移旋转初始参数Table 1 Pan & rotation initial parameters
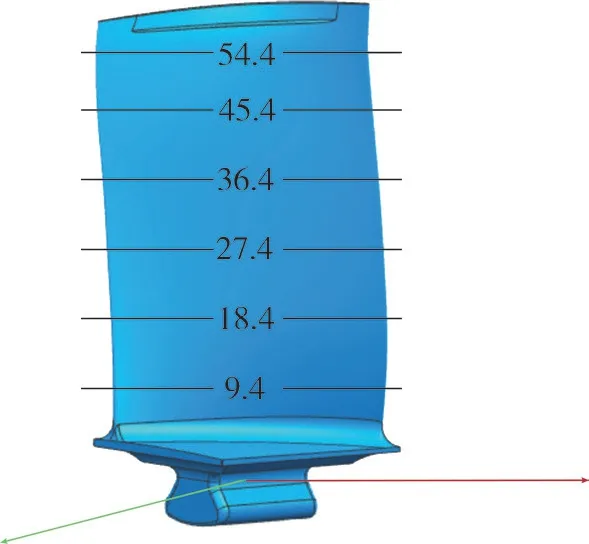
图10 叶片模型与检测高度示意图(mm)Fig.10 Diagram of blade model and inspection height (mm)
算例模型按设计图纸共检测6个截面,具体数值见表2。轮廓度公差设置为[-0.10,0.10],经过预配准算法分析得,共有2712个测量点符合轮廓度要求,所占比例为 96.86%,如图11所示,仅在叶尖位置有部分区域超出轮廓度公差,属于合格毛坯。
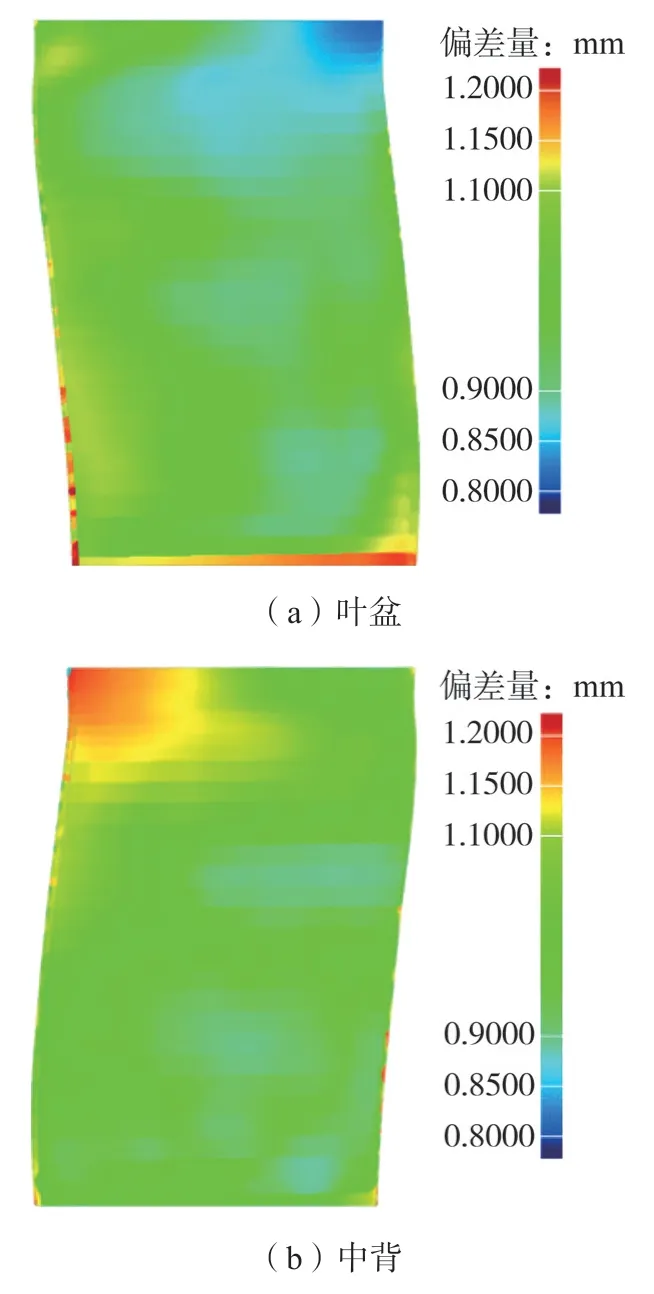
图11 预备准叶盆和叶背偏离误差曲面图Fig.11 Pre-aligned prospective pressure and suction surface deviation error surface
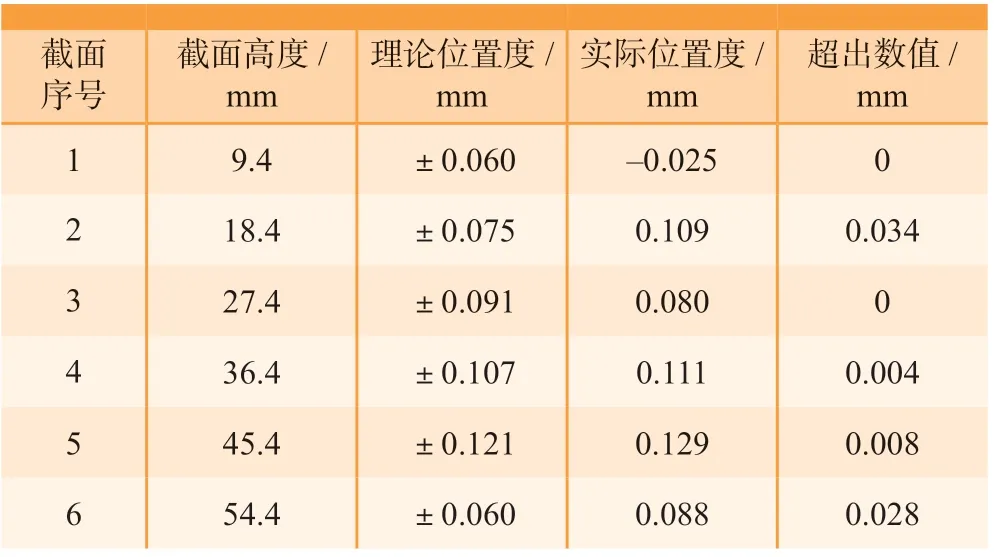
表2 叶片截面位置度值Table 2 Position value of blade section
经本研究配准算法计算后,旋转平移变换矩阵如表3所示,平移迭代过程如图12(a)所示,旋转迭代过程如图12(b)所示,可知,在6~8次时,算例结果已趋于平稳,算法迭代至27次达到收敛精度。一共用时316s,所得沿坐标轴的平移分量分别为(0.023,0.111,0.002),旋转分量分别为(0.51,0.16,0.33)。
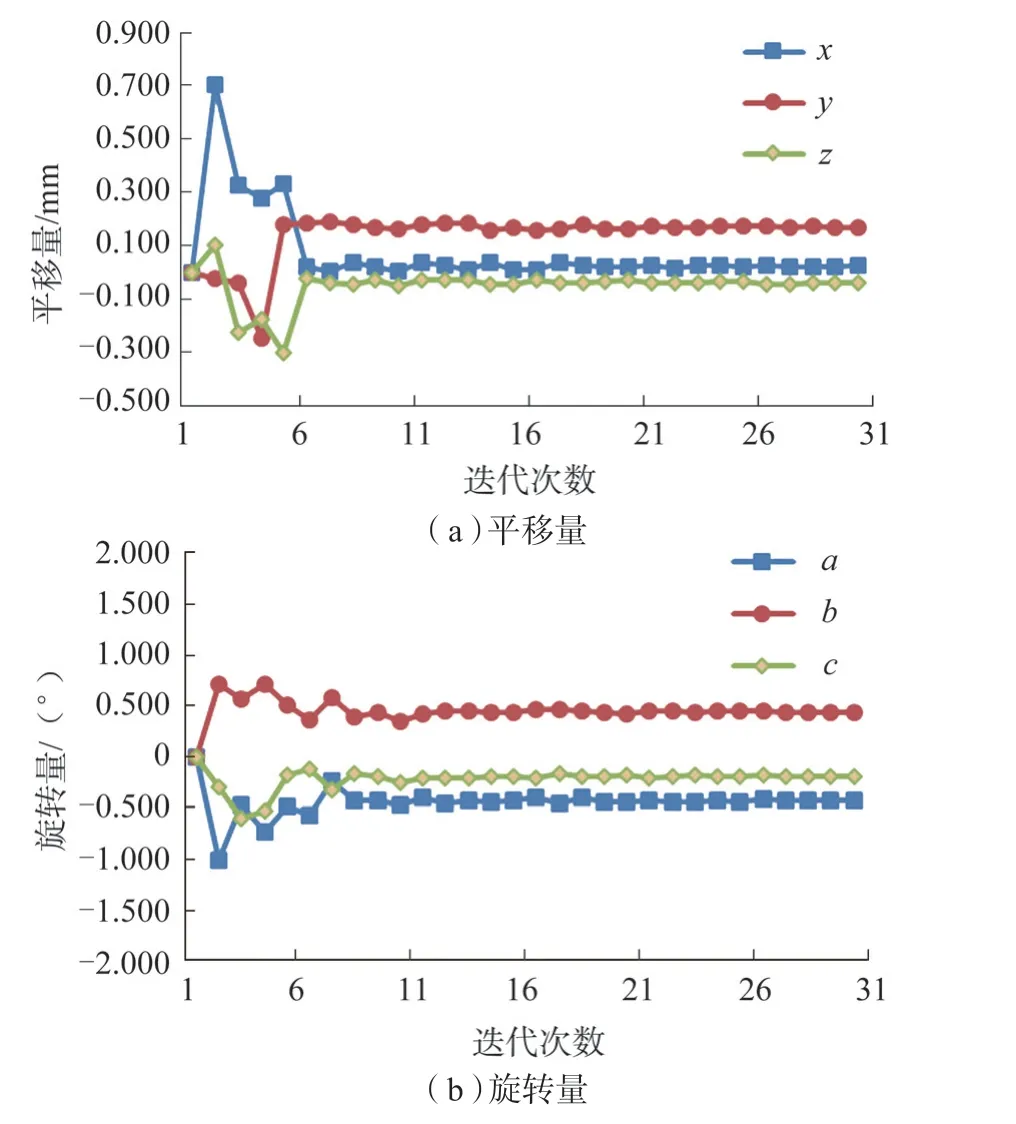
图12 平移量和旋转量迭代收敛图Fig.12 Iterative convergence diagrams of translation and rotational volume
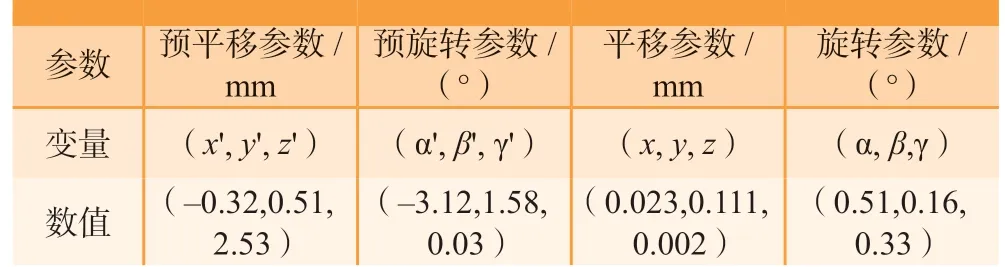
表3 精配准平移旋转参数Table 3 Precise registration translation rotation parameters
各截面高度精配准后轮廓度公差值见表4,各截面位置度与标准范围折线如图13所示,截面1~6理论位置度绝对值分别为0.060mm、0.075mm、0.091mm、0.107mm、0.121mm、0.060mm,预配准截面1~6位置度值分别为-0.025mm、0.109mm、0.080mm、0.111mm、0.129mm、0.088mm,6个截面中4个截面出现位置度超差现象;精配准截面1~6的位置度值分别 为-0.034mm、-0.071mm、-0.089mm、-0.032mm、0.014mm、0.027mm,6个全部位于位置度公差带内,位置度合格的截面数由3条增加至6条。精配准后叶盆和叶背误差曲面如图14所示,与预配准结果相比,叶尖超差区域明显减少,预配准叶片合格测量点数目为2712个,精配准后达到2784个,轮廓度公差合格率由96.86%上升为99.40%;截面配准情况如图15所示,大部分测量点均位于叶片公差带内,截面位置度误差减小。配准精度相比于4PCS与ICP组合算法在精度上有一定提高。
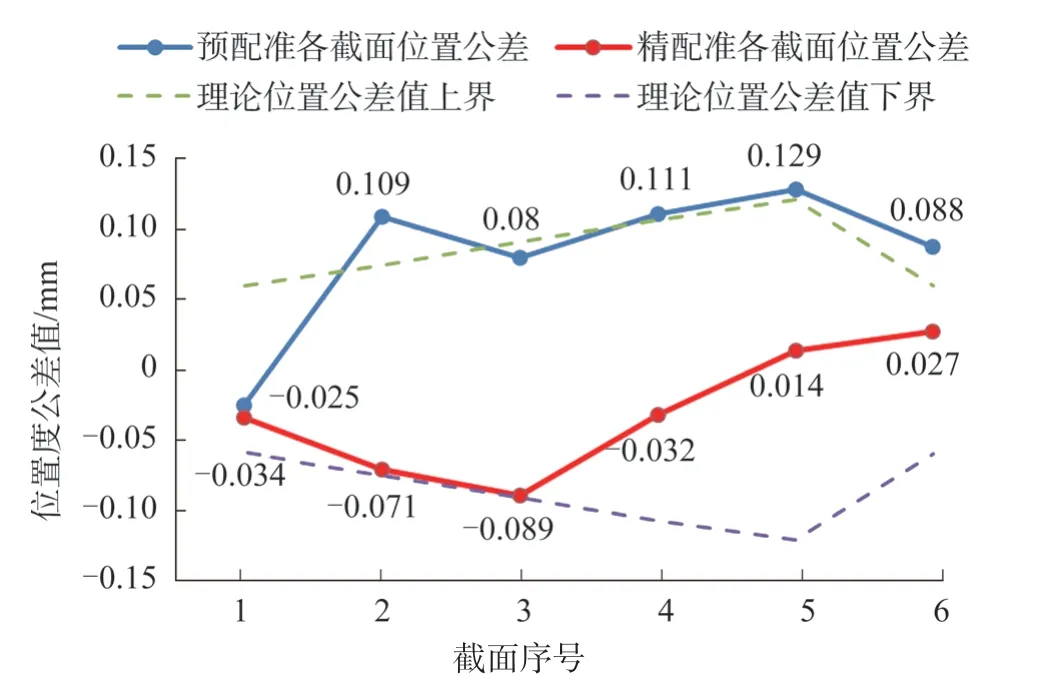
图13 各截面位置度与标准范围关系图Fig.13 Position of each section in relation to standard range
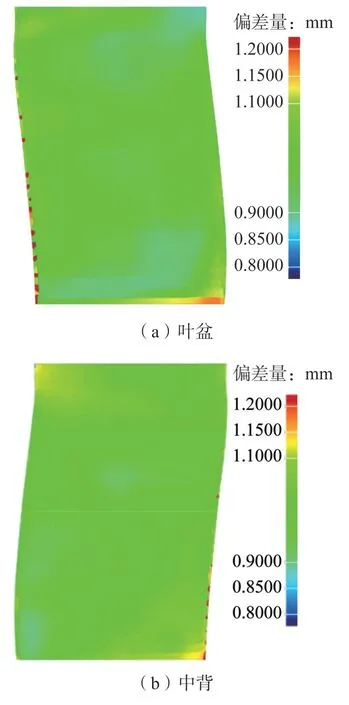
图14 精配准叶盆和叶背误差曲面Fig.14 Precision alignment of pressure and suction surface error
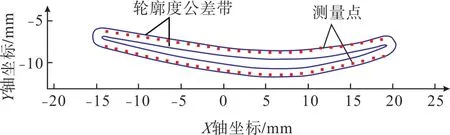
图15 截面配准情况Fig.15 Cross-sectional alignment figure
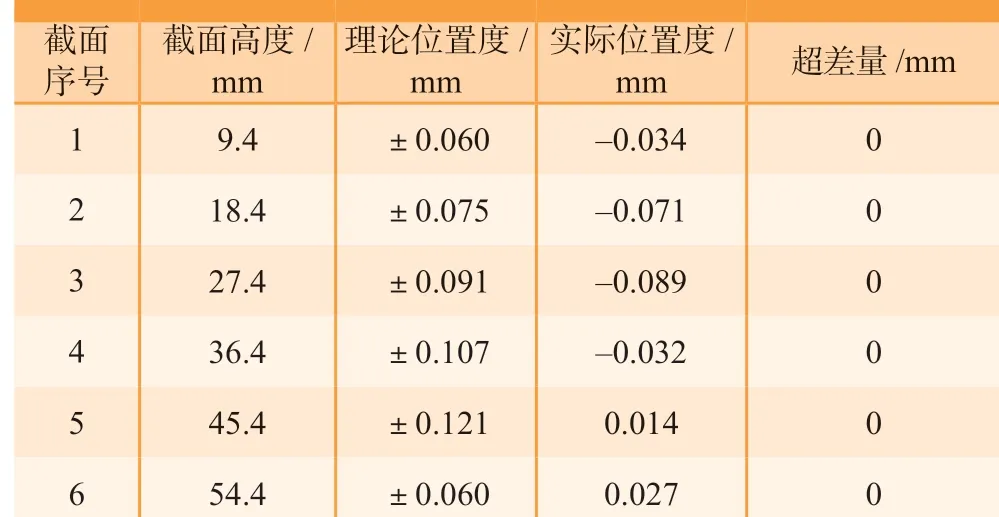
表4 精配准叶片截面位置度数值Table 4 Values for position of cross-section of precision-aligned blades
精锻叶片配准工作完成后,测量数据与理论模型已经达到余量分布与公差要求的最佳平衡,接下来构建如图16(a)所示的自由状态下的工艺几何模型,通过实际测量数据与理论模型之间的偏差关系,得到未装夹状态下的实际模型原貌,该模型表示在加工无误差的条件下实际叶片加工后的状态,得到自由状态模型后根据叶片装夹状态的在机测量数据将自由状态下的工艺几何模型变形为新的装夹状态下工艺模型,即加工用模型,如图16(b)所示。
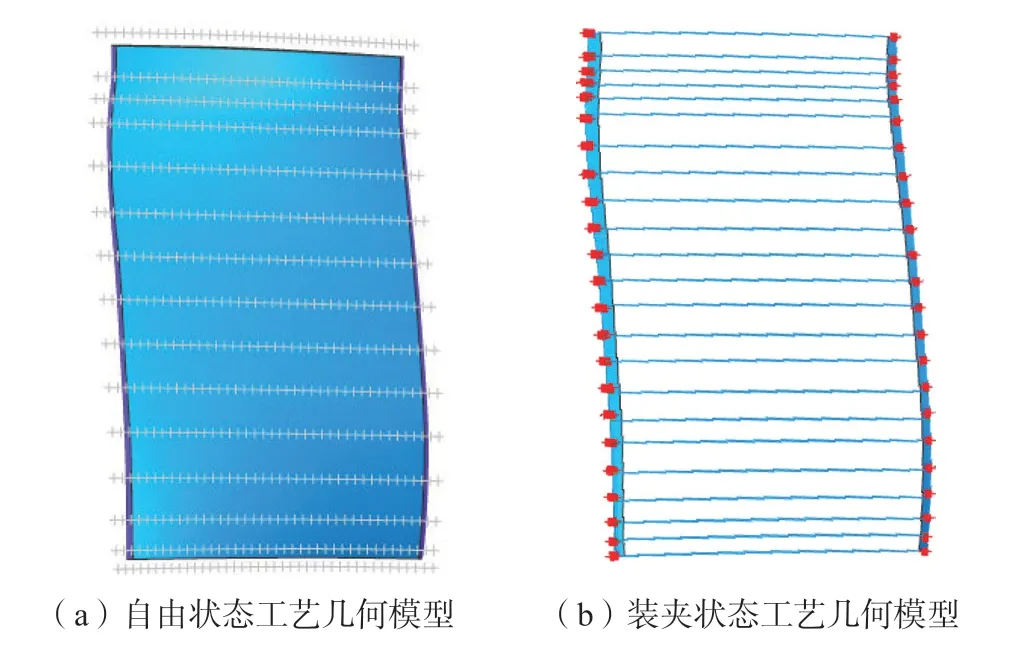
图16 自由状态和装夹状态工艺几何模型Fig.16 Geometry model in unconstraint status and clamping status
得到加工模型后,根据加工模型生成叶片前后缘与榫齿数控加工程序,前后缘加工刀轨如图17(a)所示,榫齿加工刀轨如图17(b)所示。
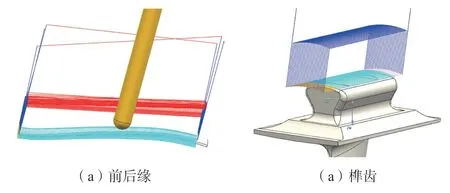
图17 前后缘和榫齿加工刀轨Fig.17 Cutting path for leading and trailing edge and tenon tooth
叶片加工完成后,采用三坐标测量机对叶片进行检测,将测得的数据输入专用检测软件BLADE软件中,并设置好相应的轮廓度、位置度等检测项目,最终生成图18所示的检测报告,其中第1列为实际偏差值,第2列为理论值,第3列为实际数据相对理论数据偏差值,第4和5列为公差带范围,根据报告可以看出,叶片位置度、轮廓度等公差均符合检测要求。
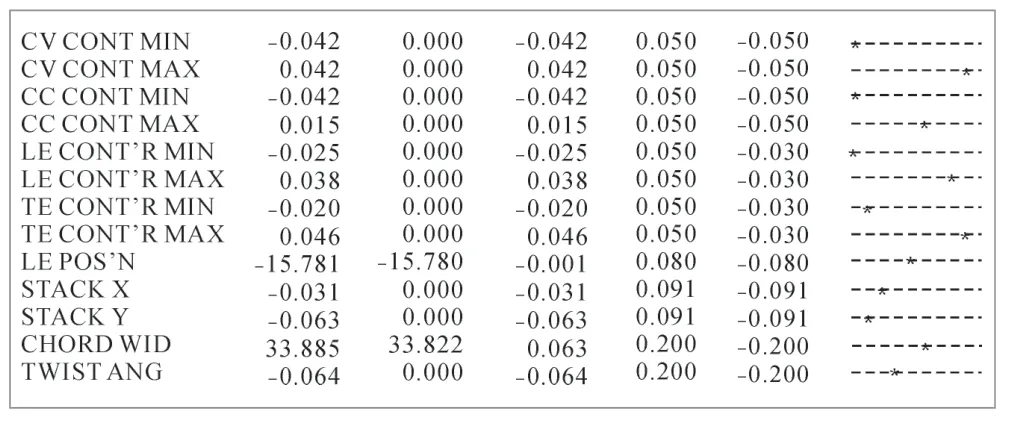
图18 叶片检测报告Fig.18 Blade examining report
叶片轮廓检测如图19所示,青色曲线代表叶型公差带,绿色曲线表示实际截面线位于公差带内。检测结果表明整个叶型轮廓位于公差带内。说明此叶片叶型检测合格,从而说明了多公差约束配准算法的有效性。
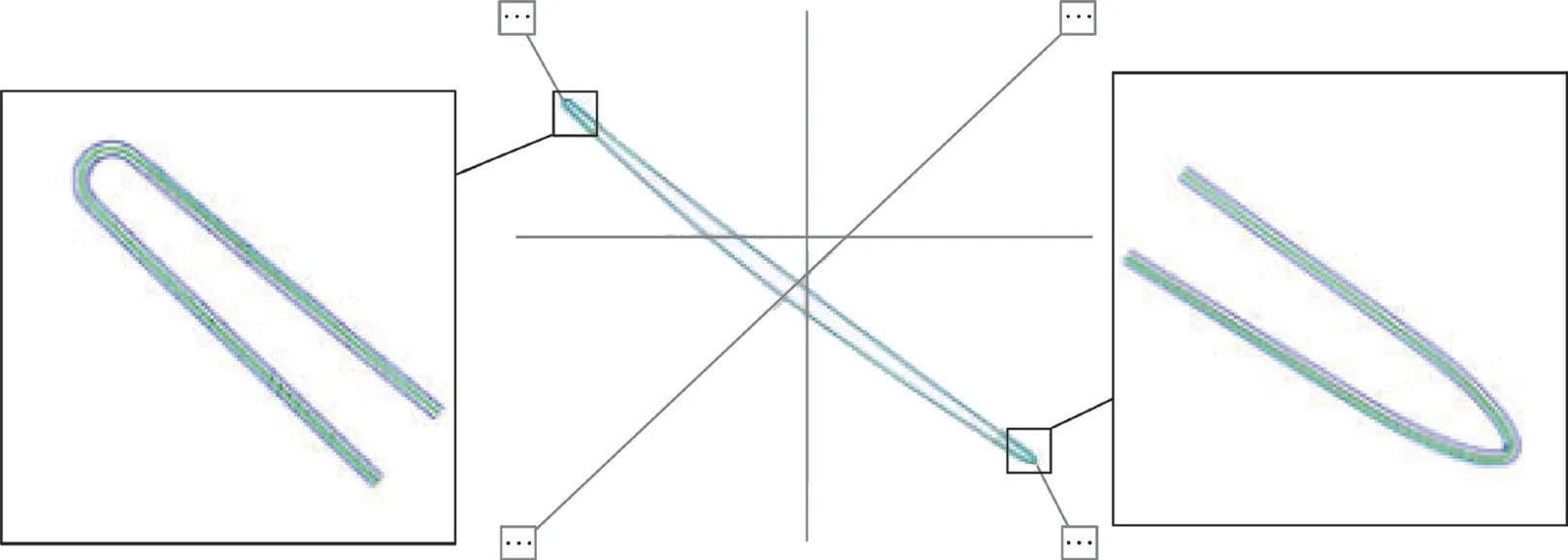
图19 BLADE软件报告Fig.19 BLADE software report
4 结论
(1)上述试验表明,本研究提出的算法能够有效降低错误匹配点对,降低配准区域的局部敏感度,提高了配准精度,配准求解采用BFGS算法大大提高了配准精度,降低了叶片截面的位置度偏差,提高了叶片的合格率。
(2)本研究存在的不足:满意度评价模型所用的满意度函数通过零件公差本身计算而来,未引入先前已经加工零件的数据集;其次叶片预对齐与精配准所用时间较长,这些是本研究在接下来的研究中要进一步完善的方向。
