机床滑动导轨微织构多目标优化设计*
2022-07-15于英华王智群要金龙
于英华,王智群,要金龙,徐 平
(辽宁工程技术大学,阜新 123000)
科技的飞速发展要求作为机械装备制造母机的机床不断向着高精、高效、高自动化、高可靠性等方向发展,而在机床中承担支承和导向作用的导轨副的承载性、摩擦磨损性、低温升性等对机床如上性能的优劣起着至关重要的作用[1-2]。表面织构以其优异的降摩擦磨损、提高承载性、降低温升、自清洁等特性,被认为是改善摩擦副性能的一种有效手段[3-10],该技术可以看作是可将先进的优化设计理论和先进制造技术融于传统刮研技术的一种新技术。优化设计理论和先进制造技术可实现根据微织构表面所需要的使役性能设计和制造出最优形貌特征参数的微织构,以最大限度发挥其对应提升微织构化摩擦副(或表面)的相关性能的作用。此外,该技术还可以克服传统刮研技术劳动强度大、生产率低和效果依赖于操作者水平的弊端。因此将微织构应用于机床滑动导轨副必将有效提升机床整机的多项性能。目前,微织构导轨方面的研究逐渐成为国内外学者的研究热点,Kovalchenko等[2]通过试验方法研究了按一定规律分布排列的圆形凹坑微织构对钢制导轨储油能力和摩擦磨损性能的影响,证明了该微织构可增加导轨表面的储油能力,进而改善其摩擦磨损性能。张赟[3]综合运用仿真分析和试验方法研究了两种不同取向的直通沟槽、两种不同取向的仿生六边形沟槽和正方形沟槽的形貌参数对钢制导轨摩擦磨损性能的影响规律,得出了最佳微织构参数。骆海波[4]通过试验方法对网状仿生微织构特征参数对导轨耐磨性的影响规律进行了研究,得出了可使滚动导轨抗摩擦磨损的性能最优的该型微织构的特征参数。张瑜等[5]研究了矩形开口非等边三角形截深织构在空化以及惯性效应的耦合作用下对导轨承载性能的影响规律,得出导轨滑块在运动过程中因惯性效应的存在使得其间的润滑油膜的承载压强有所提升,速度对微织构承载性能有较大影响,当速度大于10m/s时,流体在非对称微织构处产生的空化与惯性耦合作用对摩擦副承载性能影响更大。张东亚等[6]研究了2层沟槽微织构形貌对机床滑动滑块导轨副表面流体动压效应的影响规律,结果表明,当所构筑的沟槽体积相同时,2层沟槽的润滑油膜承载压强提升效果优于1层沟槽织构;随着第2层微织构沟槽深度的增加,导轨承载性能先增大后减小,并存在可使导轨承载压力最大的沟槽深度。
综上所述,迄今为止国内外学者对微织构在导轨中应用方面的研究主要集中在圆型或矩形开口凹坑和沟槽微织构导轨承载能力以及摩擦磨损性能方面。本研究依据响应面分析理论、运用CFD方法研究即有利于增大寻优空间又相对便于制造的椭圆开口偏置类抛物线微织构特征参数对导轨承载压强、摩擦系数、温升及乏油状态下的接触应力等多项性能的影响规律,并运用多目标优化设计理论对微织构特征参数进行优化,旨在为充分挖掘微织构对提升导轨乃至其他摩擦副综合性能的潜能提供参考。
1 原型导轨的选取及其性能分析
1.1 原型导轨的选取
本研究选取矩形滑动滑块导轨为研究原型,其简化模型如图1所示,其运行速度、材料性能参数以及所用润滑油参数如表1所示。
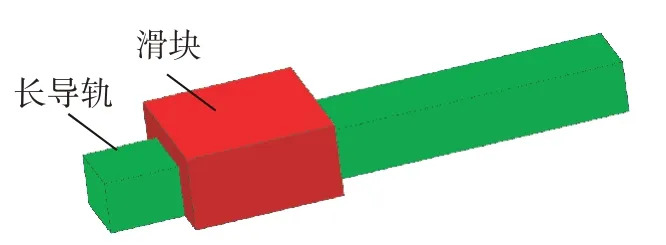
图1 导轨简易模型Fig.1 Simple model of guide
1.2 滑动导轨流体润滑理论
当导轨在液态润滑状态下运动时,导轨副之间的润滑油膜遵循层流状态下的二维稳态不可压缩润滑油流体动压Reynolds方程,即
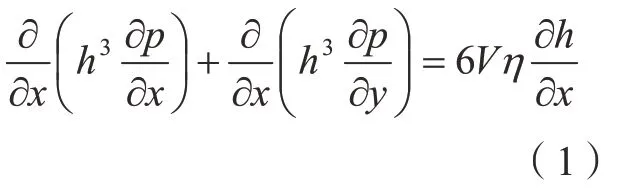
式中,p为导轨间的压力,Pa;h为油膜厚度,mm;η为润滑油黏度,Pa·s;V为导轨副的相对滑动速度,m/s,在稳态状态下忽略在油膜厚度方向上的速度矢量,即∂h/∂t=0。忽略润滑油在导轨滑块表面沿横纵向的热传导,其间润滑油的比热容以及传导系数为固定常数,所以可得能量控制方程为
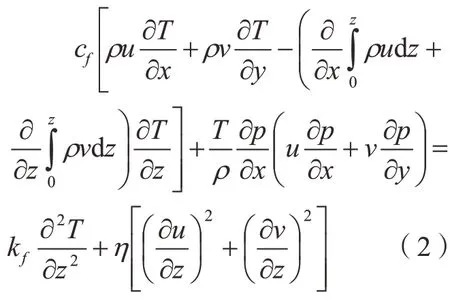
式中,ρ为润滑油密度,kg/m3;cf为滑油的比热容,J/ (kg·℃);kf为热传导系数,W/ (m·℃);u、v分别为滑动滑块导轨副在x、y方向的速度分量,m/s。
根据式(1),对润滑油膜承载压强p(x,y)积分进而得到润滑油膜的承载量,即承载力公式为
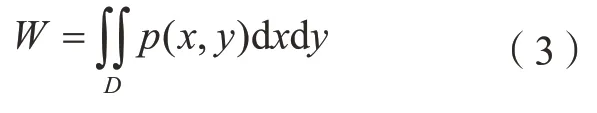
润滑油膜作用在导轨副的摩擦力可通过对导轨副之间的流体剪应力沿整个面积积分求得,即
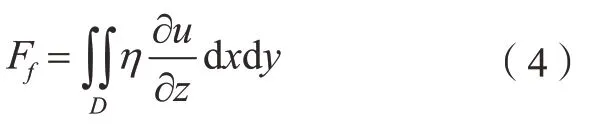
于是可得导轨副之间的摩擦系数μ为
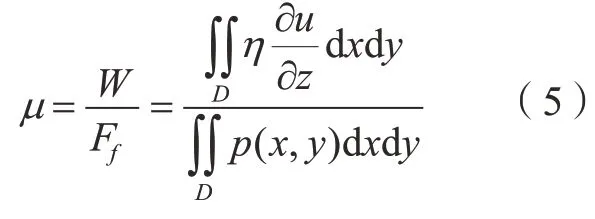
根据式(2),对滑动滑块导轨副间的润滑油膜温度T(x,y)积分进而可得油膜的平均温度为
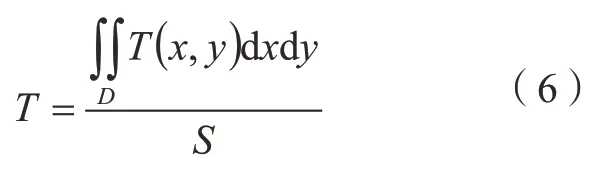
式中,S为油膜面积,mm2; {yxD= ),(
1.3 流体润滑条件下原型导轨相关性能有限元仿真分析
为在不影响仿真分析结果的前提下提高仿真分析效率,选取机床导轨的15mm×15mm局部单元对原型导轨摩擦副相关性能进行有限元仿真分析。设定所研究的滑动滑块导轨副两表面处于流体润滑状态,油膜厚度h为10μm[9],依此建立导轨仿真分析模型。根据滑块导轨的实际工况,设定长导轨表面固定,滑块在其上以2m/s的速度向右运动,对导轨模型施加的边界约束如图2所示。采用Multi Zone Quad/Tri Method方法,对其三维模型进行网格划分,如图3所示,将能量方程打开,按照表1输入润滑油的性能参数。润滑油流体域边界条件的设定如下:导轨副间润滑油膜入口边界为压力入口,出口边界为压力出口,进油温度设为30℃,均设为1个大气压,润滑油膜顶层边界速度设为2m/s,润滑油膜底层边界速度为0。运用 Ansys 软件进行后处理,最终求得如图4所示的油膜上表面的承载压强、切应力以及温度的分布云图。根据式(3)~(6)计算出导轨的承载压强为100218Pa,切应力为14010.48Pa,摩擦系数为0.14,平均温度为42.08℃。
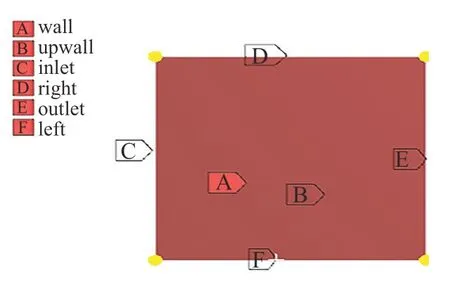
图2 边界约束定义Fig.2 Definition of boundary constraints

图3 边界条件设定Fig3 Boundary condition setting
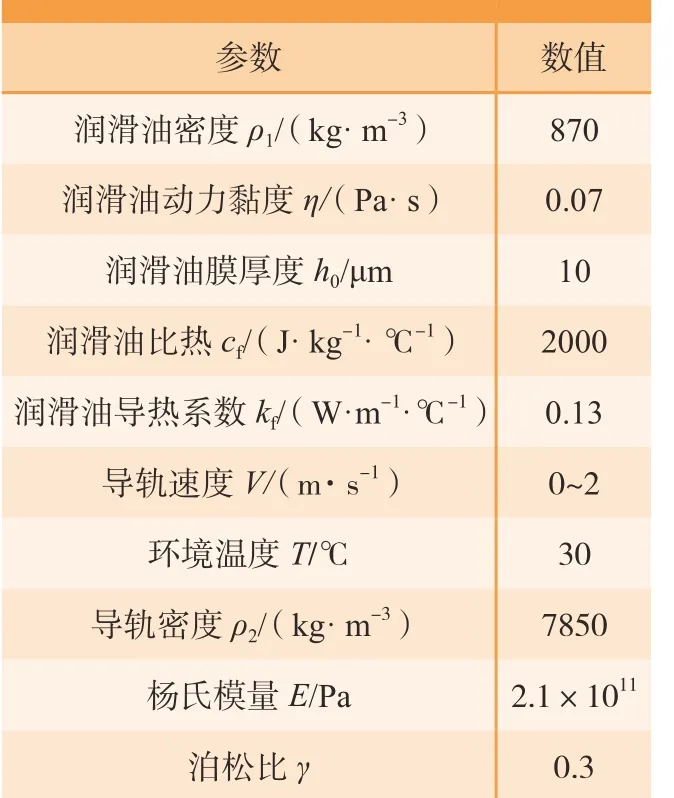
表1 原型导轨及润滑油的主要性能参数Table 1 Main performance parameters of prototype guide rail and lubricating oil
由图4可见,沿着滑块的运动方向油膜压强和温度均呈上升的趋势,而油膜的切应力则无明显变化。导轨副间的润滑油膜压强越大,即导轨的承载力越大;切应力越小,摩擦系数越低,越有助于减少诱发摩擦自激振动的概率[11],并越有利于降低运行能耗,进而降低成本、提高节能环保性;温升越低,越既可减小导轨副的热变形,又可减少润滑油黏度的变化,这些对于提高导轨的精度保持性就越有利。
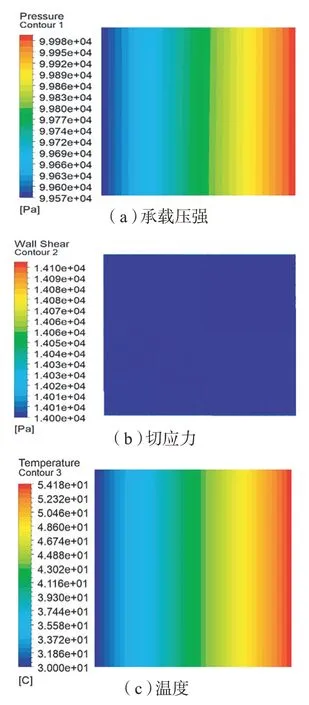
图4 原型导轨性能仿真分析云图Fig.4 Simulation analysis cloud diagram of prototype guide performances
1.4 原型导轨低速乏油状态下接触应力仿真分析
当机床滑动导轨处于启动、停止、低速工况时,其滑动导轨摩擦副间处于乏油状态,摩擦表面表现为未形成完整的润滑油膜的干摩擦或边界摩擦情况,由于滑动滑块导轨副接触面的应力会影响最终的润滑效果,为此有必要分析导轨低速乏油状态下的接触应力。
本研究利用Ansys Workbench软件对滑动滑块导轨副模型进行摩擦副接触应力的仿真分析。为了提高计算效率,选取滑动滑块导轨副的15mm×5mm×3mm典型局部单元进行仿真分析。利用UG软件建立其三维模型,按照表1赋予材料性能参数,设置滑块为接触面,导轨设置为目标面,设置滑块的接触方式为摩擦接触,摩擦系数设置为0.1;将导轨下表面进行固定约束,滑块的上表面施加1MPa的压强,如图5(a) 和(b)所示;滑块的移动速度为1000μm/s,沿导轨上表面匀速向右运动,如图5(c)所示;最终求得滑块运动1s后导轨接触应力分布如图5(d)所示。
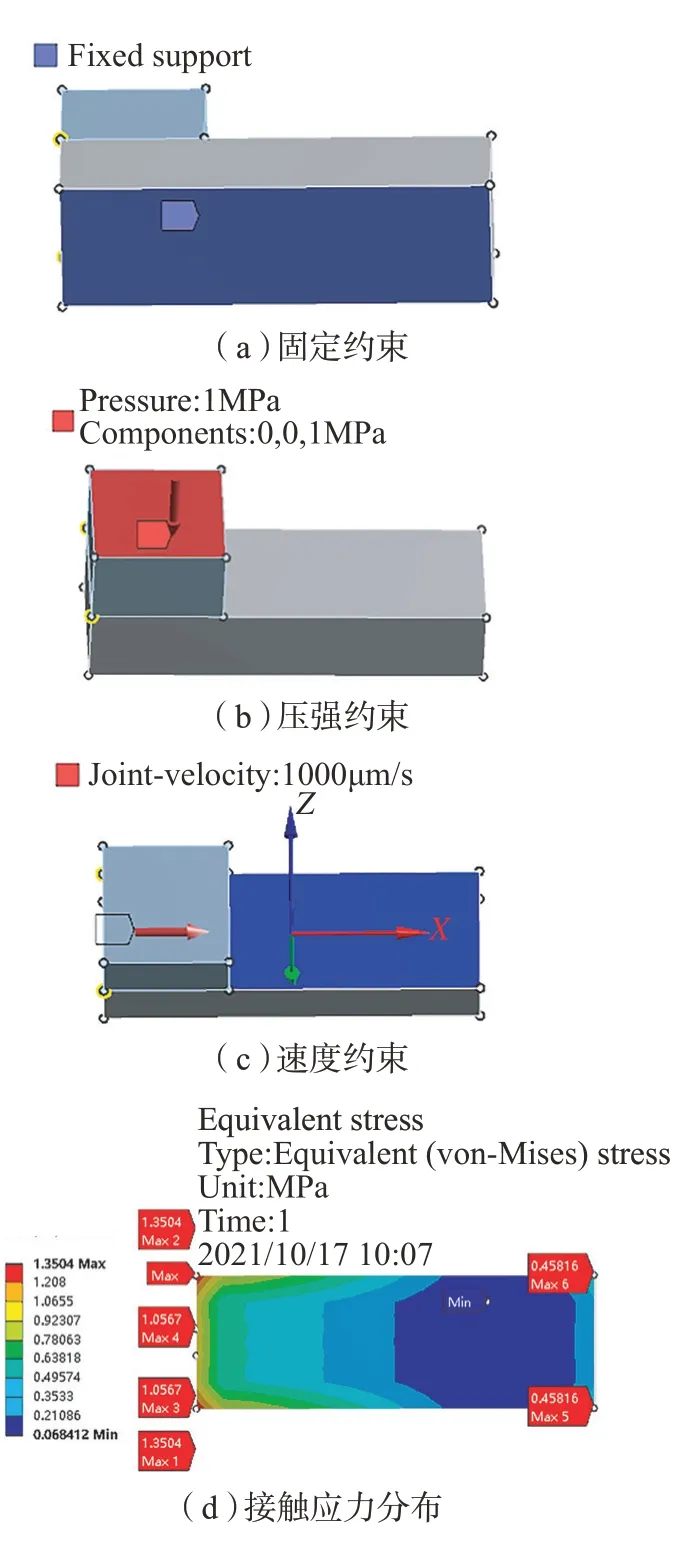
图5 接触应力分析约束条件设置及结果Fig.5 Constraint conditions setting and results of contact stress analysis
由接触应力分布图可知,导轨副表面上的最大接触应力为1.3504MPa,分布在导轨摩擦接触面边缘处。
2 微织构构型及其形状参数对导轨性能影响规律研究
2.1 微织构单元胞孔构筑
本研究构筑的表面微织构单元胞孔为图6所示的椭圆开口偏置类抛物线孔型,即在单元尺寸Lx×Ly=1500μm×800μm的导轨副表面加工长半轴长为A,短半轴长为B的椭圆开口,抛物线的类型系数Rho(即凹坑深度与类抛物线进出口切线交点距开口表面垂直距离的比值)为C,抛物线最深点距椭圆中心的偏置距离(偏置量)为D,深度为E的偏置类抛物线截深的凹坑微织构。由于其椭圆开口本身具有各向异性的特点,而且在特定条件下又可以转化为圆形; 加之其在深度方向的截形为偏置类抛物线形,特殊情况下可以转化为对称抛物线和球冠形。因此这样可使研究中对微织构单元胞孔的结构参数和排布方式的寻优空间增大,以利于获得更优的微织构形式。

图6 单元胞孔结构示意图Fig.6 Schematic diagram of unit cell structure
2.2 微织构形状参数对导轨性能影响规律
通过响应面理论和Design-Expert软件研究微织构形状参数对导轨性能影响规律及参数优化。利用Design-Expert软件中的CCD中心复合设计方法构造出如表2所示的微织构形状参数五因素五水平的32组三维结构模型,对其承载压强及摩擦系数进行仿真分析。
根据表2中的仿真分析结果,应用软件中的响应面分析模块生成微织构形状参数两两因素交互作用对承载压强和摩擦系数的影响曲面,限于篇幅,本研究只给出承载压强的相应曲面,如图7所示。
表2 微织构形状参数因素水平与结果Table 2 Level of microtexture shape parameter factors and results
由图7(a)~(d)可知,当Rho和其他因素比较时,在Rho方向上的等高线最为密集且以承载压强为目标的响应面颜色变化更明显,即Rho对导轨承载压强的影响最显著;由图7(f)和(g)可知,其他4个形状参数相比较时,长半轴方向上的等高线较另外3个参数密集且响应面颜色变化更明显,即长半轴较另外3个参数显著;由图7(h)和(i)可知,当深度、偏置量、短半轴相比较时,深度方向上等高线较其他两个参数密集且响应面颜色变化更明显,即深度较偏置量、短半轴对导轨承载压强的影响更显著;最后通过图7(j)可知,当偏置量和短半轴径作比较时,偏置量方向上等高线更密集且响应面颜色变化更明显,即偏置量对导轨承载压强的影响更显著。最终可以判断5个形状参数对承载压强的影响程度次序为Rho>长轴半径>深度>偏置量>短轴半径。同理可得5个形状参数对摩擦系数的影响次序为长轴半径>短轴半径>Rho>深度>偏置量。
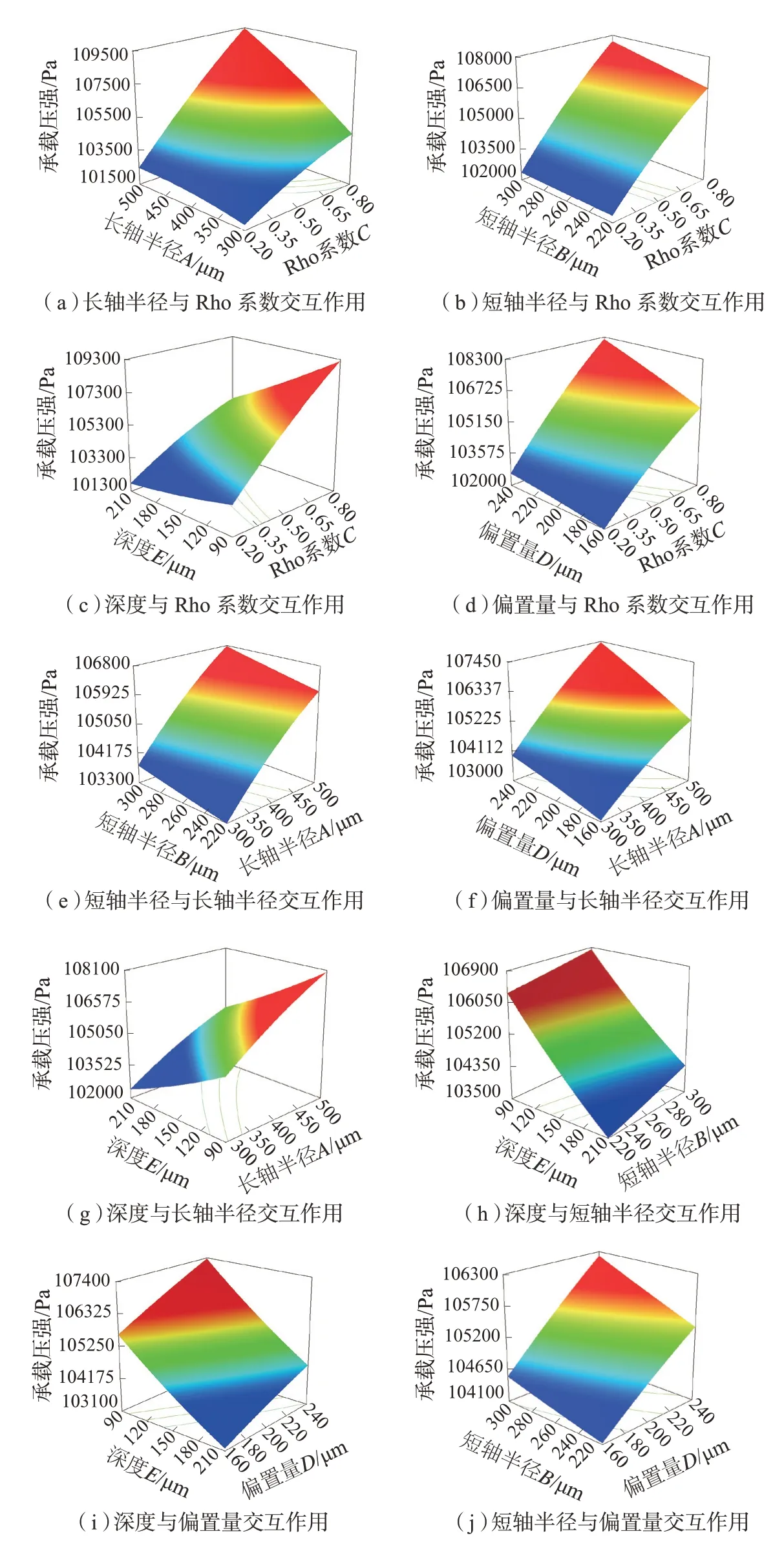
图7 承载压强对形状参数的响应面Fig.7 Response surfaces of shape parameters on bearing pressure
3 微织构形状参数优化设计
为寻求可使导轨承载压强最大、摩擦系数最小的微织构形状参数,以微织构的承载压强最大、摩擦系数最小为目标函数,以微织构的承载压强大于无织构承载压强以及微织构的摩擦系数小于无织构的摩擦系数为约束条件;以前叙5个微织构形状参数为设计变量,最终建立优化数学模型为

式中,f1(P)为微织构单元胞的承载压强,Pa;f2(P)为微织构单元胞的摩擦系数;P1、P2、P3、P4、P5分别为微织构形状参数A、B、C、D、E。
依据式(7)优化模型,通过CCD中“Optimization”优化模块可得微织构的最优形状参数(对最初优化得到的5个参数进行了圆整):A为450μm,B为278μm,C为0.65,D为220μm,E为135μm。根据上述得到的单元胞最优结构参数,构造单元微织构三维模型并进行流体仿真,得到其压强分布云图如图8(a)所示。为对比分析,对相同尺寸单元的未织构导轨间油膜的压强进行仿真分析,得到其压强分布云图如图8(b)所示。
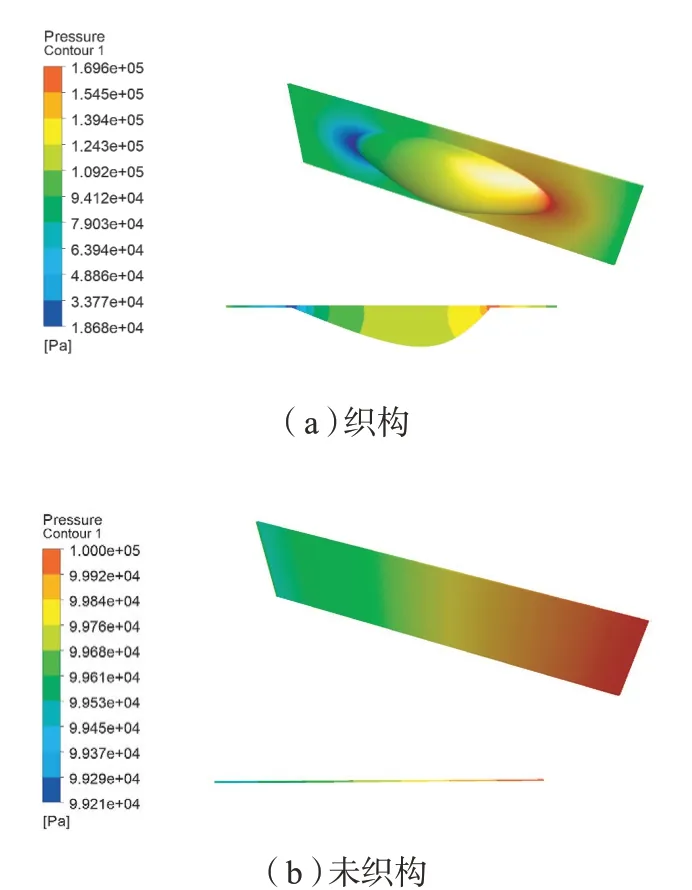
图8 单元压强分布云图Fig.8 Pressure distribution cloud diagram of elements
由如上分析得到的油膜压力,依据式(3)~(5)可得织构和未织构单元油膜承载压强分别为106838.63Pa和100704.61Pa,而摩擦系数分别为0.106和0.139,即织构相较于未织构单元的油膜承载压强提高了6.09%,而摩擦系数却降低23.74%。
4 微织构分布参数对导轨性能影响规律研究及优化
4.1 对导轨性能影响规律研究
由于微织构摩擦副轴承性能不仅与其结构参数相关,还与其在摩擦副表面的分布参数相关。为此有必要在前文获得微织构最优结构参数基础之上,研究微织构分布参数对导轨性能影响规律,并对分布参数进行优化设计。
微织构导轨的简易模型如图9所示,其中微织构的分布参数包括3个,分别为微织构在导轨表面分布的纵向和横向间距(F、G)和椭圆开口长轴与运动方向之间的夹角(H)。设计分布参数三因素五水平的试验方案,并应用Design-Expert 10软件中的Box-Behnken响应面设计方法构造出17组三维结构模型,对其承载压强、摩擦系数及温度进行仿真分析,结果如表3所示。
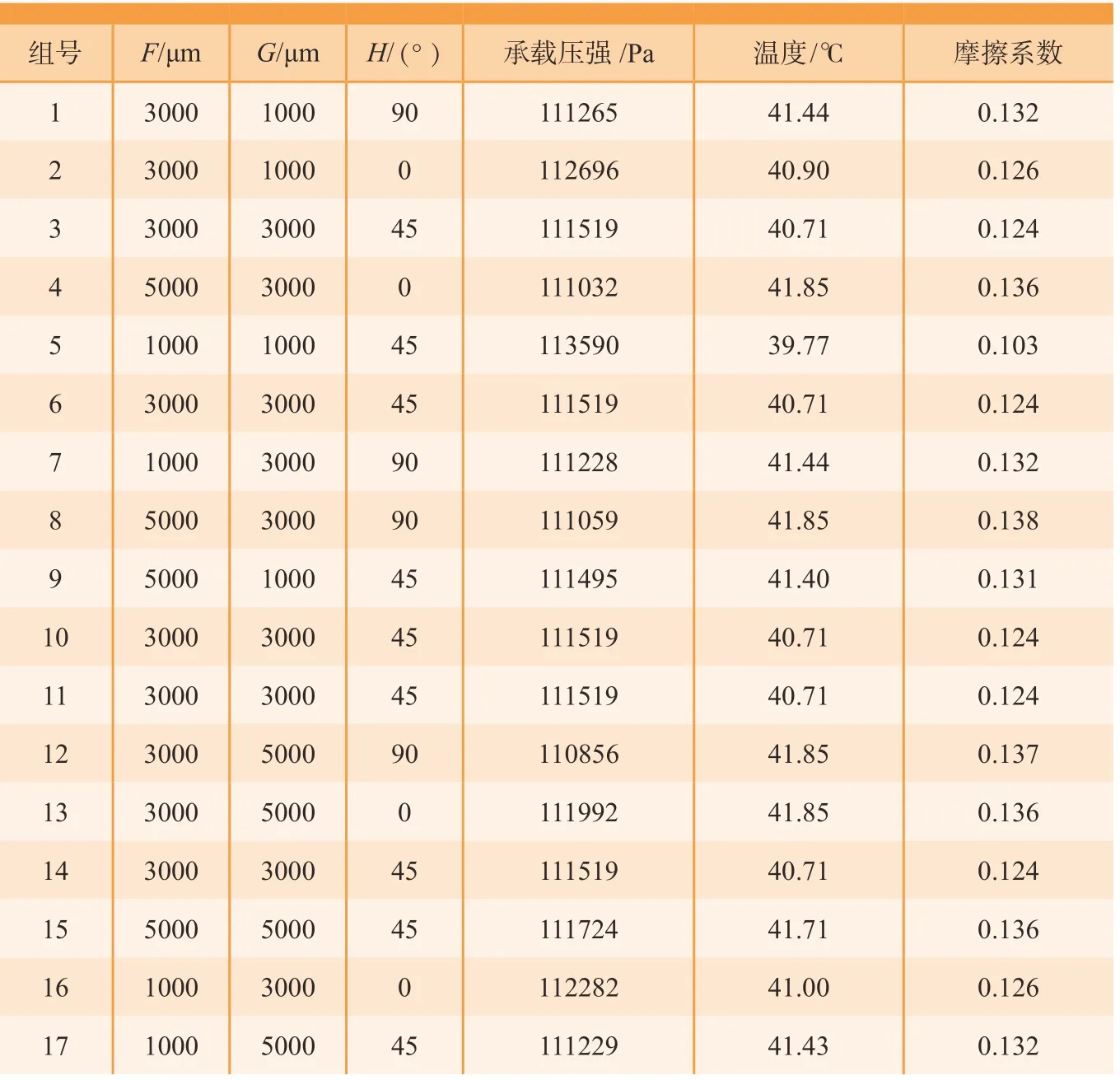
表3 分布参数试验方案设计与结果Table 3 Design of distributed parameter test and results
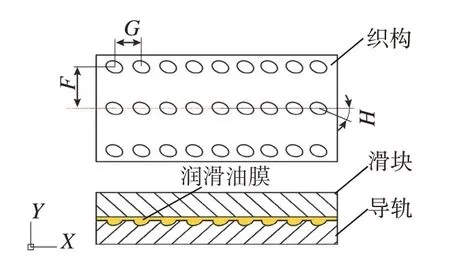
图9 微织构导轨副简易模型Fig.9 Simple model of micro texture sliding guide pair
进一步生成微织构分布参数两两因素交互作用对承载压强、摩擦系数和温度的影响规律曲面如图10所示。
参照前文中依据响应曲面判断影响因素对考察目标影响程度大小顺序的方法,依据图10可以得出微织构的3个分布参数对导轨的承载压强、摩擦系数和温度的影响程度大小分别为角度>横向间距>纵向间距、纵向间距>横向间距>角度、横向间距>纵向间距>角度。

图10 分布参数对油膜性能的响应面Fig.10 Response surface of distributed parameter factors on oil film performances
4.2 优化设计
为寻求可使导轨的承载压强高、摩擦系数低和温升小的微织构分布参数,以导轨承载压强最大、摩擦系数最小、温度最低为目标函数,以前叙3个微织构分布参数为设计变量,建立优化数学模型为
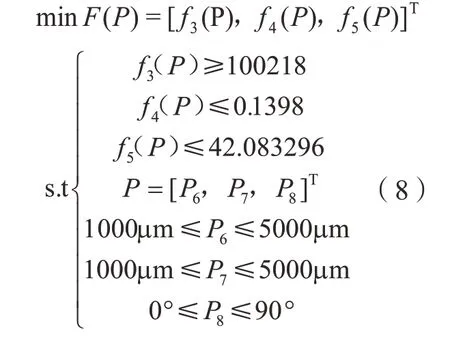
式中,f3(P)为微织构滑动滑块导轨副的承载压强,Pa;f4(P)为摩擦系数;f5(P)为温度,℃;P6、P7、P8分别为微织构分布参数F、G、H。
基于如上优化模型通过Box-Behnken优化模块,最终得到最优微织构形状参数(对最初优化得到的3个参数进行了圆整):F和G均为1000μm;H为32°。
4.3 最优特征参数微织构导轨相关性能研究
4.3.1 液体润滑状态下微织构导轨相关性能研究
建立最优特征参数微织构导轨副之间油膜三维模型,将其导入Fluent并进行网格划分,边界条件施加同原型导轨,得到油膜表面压强、切应力及温度分布云图如图11所示。进一步计算得到导轨的承载压强115402.62Pa、摩擦系数0.103和平均温度38.74℃,与未织构原型导轨 的100218Pa、0.140和42.08℃相比,前者提高了15.15%,而后两者分别降低了26.43%和7.94%。
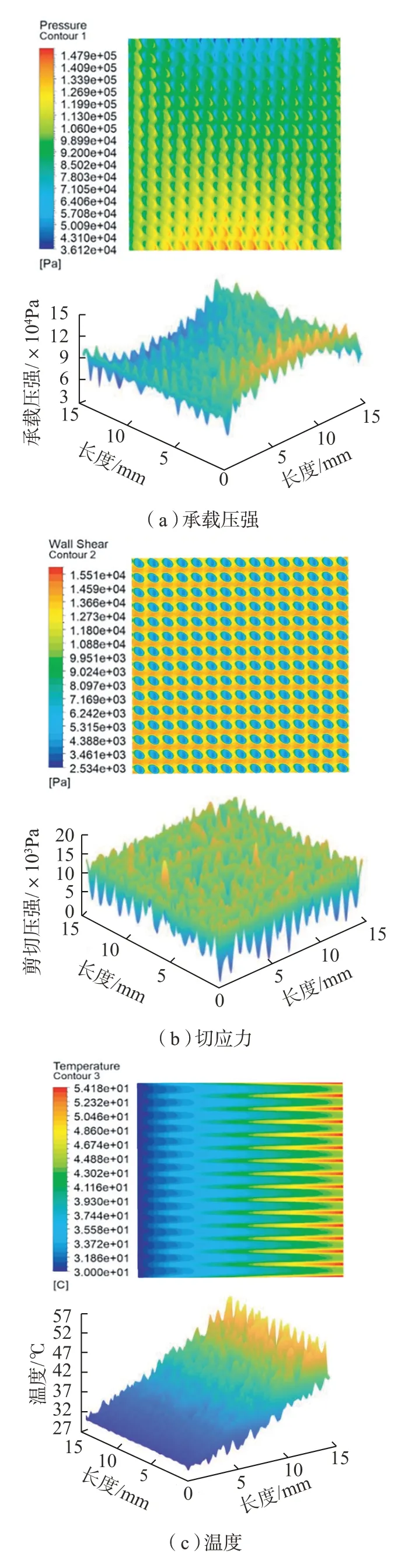
图11 最优微织构导轨副性能分布云图Fig.11 Performance distribution clouds diagram of optimal micro-texture guide pair
4.3.2 乏油状态下微织构导轨接触应力仿真分析
建立与前文中原型导轨相同外形尺寸的织构导轨三维模型如图12(a)所示,对其进行网格划分并设置同原型导轨的接触及约束条件,最终得到乏油状态下微织构导轨接触应力云如图12(b)所示。
对比图12(b)和图5(d)可知,微织构导轨最大应力为1.4207MPa,比原型接触面的最大应力值1.3504MPa略大,但其并不在接触表面上而是分布在微织构内部,对接触面的润滑基本没有影响,而在接触面处的最大接触应力为1.2412MPa,较织构前的最大接触应力1.3504MPa降低了8.09%。最大值也分布在摩擦副表面边缘,这与张赟[3]所研究的圆孔微织构结论一致。可见,在低速重载乏油状态下,导轨上织构椭圆开口偏置类抛物线微织构后能够有效减小接触应力,进而有利于润滑油膜的形成改善导轨的摩擦磨损性。
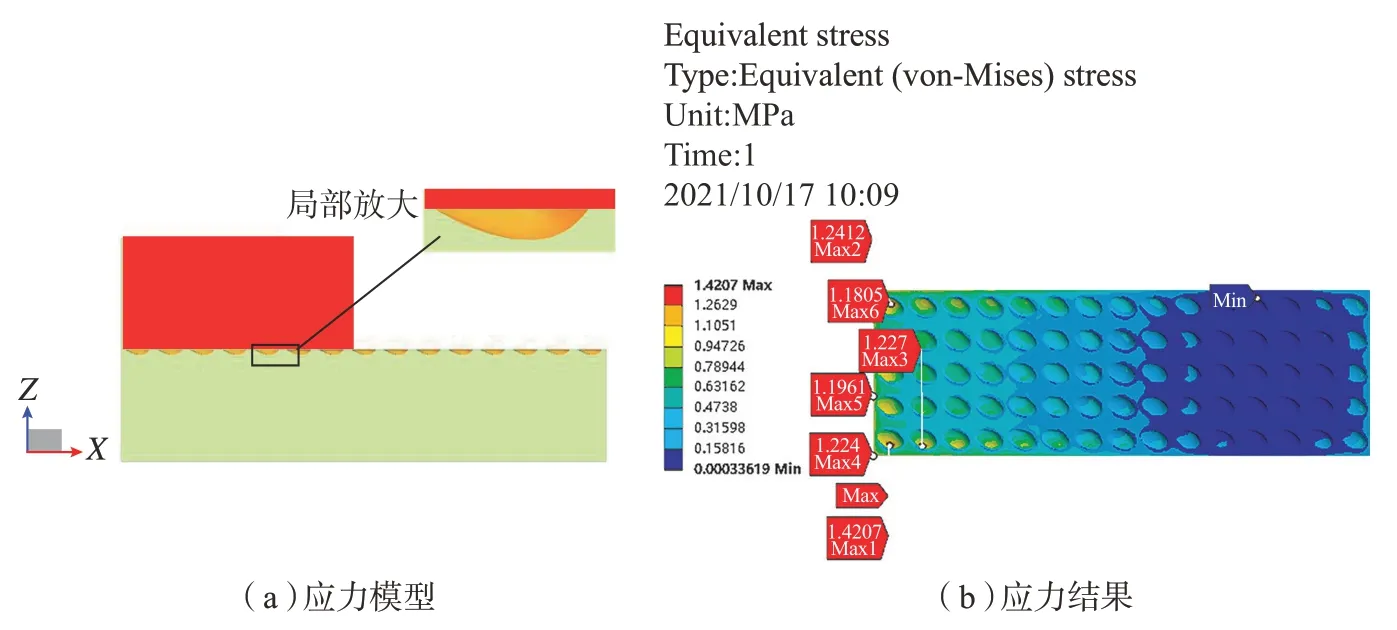
图12 乏油状态下微织构导轨接触应力模型及结果Fig.12 Contact stress model and results of microtextured guide under lack of oil condition
5 结论
(1)在滑动导轨副定导轨上织构椭圆开口偏置类抛物线微织构时,位置形状参数对导轨承载压强和摩擦系数的影响程度大小顺序分别为Rho>长轴半径>深度>偏置量>短轴半径、长轴半径>短轴半径>Rho>深度>偏置量。以承载压强最大摩擦系数最小为目标进行优化得到的最优微织构结构参数为椭圆长半轴长450μm、椭圆短半轴长278μm、深度135μm、偏移量220μm、Rho系数为0.65。最优形状参数微织构单元承载压强较原型提升6.09%,摩擦系数较原型降低23.74%。
(2)织构的3个分布参数对导轨的承载压强、摩擦系数和温度的影响程度大小顺序分别为角度>横向间距>纵向间距、纵向间距>横向间距>角度、横向间距>纵向间距>角度。以承载压强最大、温度和摩擦系数最小为目标优化得到的最优分布参数为纵、横向间距均1000μm、椭圆开口长轴与运动方向之间的夹角32°。
(3)最优特征参数椭圆开口偏置类抛物线微织构导轨的承载压强、摩擦系数和平均温度分别为115402.62Pa、0.103和38.74℃,与原型未织构导轨的100218Pa、0.140和42.08℃相比,前者提高了15.15%,而后两者分别降低了26.43%和7.94%;在乏油状态下,椭圆开口偏置类抛物线微织构导轨最大接触应力为1.2412MPa,较原型未织构导轨的1.3504MPa降低了8.09%。
