探寻凹凸本质 凝炼致用模型

东莞市第四高级中学(523220) 王文涛

一.试题呈现

题目1 (2021年广东省中考第25题节选)二次函数y=ax2+bx+c的图像过点(−1,0),且对任意实数x,都有4x−12≤ax2+bx+c≤2x2−8x+6,求该二次函数的解析式.

题目2 (2020年高考江苏卷第19题节选)已知关于x的函数y=f(x),y=g(x)与h(x)=kx+b(k,b∈R)在区间D上恒有f(x)≥h(x)≥g(x),若f(x)=x2+2x,g(x)=−x2+2x,D=(−∞,+∞),求h(x).

这两道题的形式新颖,表面看起来考察的是二次函数恒成立问题,但实质背景是凹凸函数的切线方面的几何特征.下面从一元函数微分学的视角给出新的解答和推广.

二.解法探究

以题目1 为例,采用两边夹的思想,先必要性求值,再证明充分性.

解因为二次函数y=ax2+bx+c的图像过点(−1,0),所以有a−b+c=0.又因为对任意实数x,都有4x−12≤ax2+bx+c≤2x2−8x+6,令x=3,有0≤9a+3b+c≤0,所以9a+3b+c=0,与a−b+c=0联立,解得b=−2a,c=−3a.

设f(x)=4x−12,g(x)=ax2+bx+c,h(x)=2x2−8x+6,则f(x)≤g(x)≤h(x),f(3)=g(3)=h(3).设F(x)=g(x)−f(x)=ax2+(b−4)x+c+12,F′(x)=2ax+b−4,由上知F(x)≥0=F(3),则x=3 是F(x)的极小值点,由费马引理得F′(3)=0,即2a×3+b−4=0,所以a=1,b=−2,c=−3.

下证充分性.当a=1,b=−2,c=−3,g(x)−f(x)=x2−6x+9=(x−3)2≥0,h(x)−g(x)=x2−6x+9=(x−3)2≥0,所以f(x)≤g(x)≤h(x),所以所求的解析式为y=x2−2x−3.

注f(x)=4x−12 是g(x)与h(x)在x=3 处的公切线.

三.相关背景

为行文方便起见,以下根据文献[1]给出函数凸(凹)的定义以及相关定理和几何特征.

定义1 设f为定义在区间I上的函数,若对I上的任意两点x1,x2和任意实数λ∈(0,1),总有f(λx1+(1−λ)x2)≤λf(x1)+(1−λ)f(x2),则称f为I上的凸函数.反之,如果总有f(λx1+(1−λ)x2)≥λf(x1)+(1−λ)f(x2),则称f为I的凹函数.

定理1 设f为定义在区间I上的可导函数,则下述论断互相等价:1◦f为I上的凸(凹)函数; 2◦f′为I上的增(减)函数;3◦对I上的任意两点x1,x2,有f(x2)≥f(x1)+f′(x1)(x2−x1)(f(x2)≤f(x1)+f′(x1)(x2−x1)).

定理2 设f(x)为区间I上的二阶可导函数,则在I上f为凸(凹)函数的充要条件是f′′(x)≥0(f′′(x)≤0),x∈I.

通过以上论断3◦我们能得到凸(凹)函数的几何特征:凸(凹)函数的曲线总是在它的任一切线的上方(下方).

四.三种推广模型

性质1 设f(x)和g(x)为开区间I上的二阶可导函数,f(x)≥g(x),f(x0)=g(x0),且满足下列三个条件之一:(1)f(x)为凸函数,g(x)为凹函数;(2)f(x)为凸函数,g(x)为凸函数;(3)f(x)为凹函数,g(x)为凹函数,则f(x)和g(x)必存在公切线h(x),且对应三个条件有(1)f(x)≥h(x)≥g(x);(2)f(x)≥g(x)≥h(x);(3)h(x)≥f(x)≥g(x).

证明设F(x)=f(x)−g(x),由条件知F(x)≥0=F(x0),则x0为函数F(x)的极小值点,由费马引理得F′(x0)=0,即f′(x0)=g′(x0),又因为f(x0)=g(x0),所以f(x)和g(x)在x=x0处存在公切线h(x).后略.

以上三个条件对应了三种推广模型,分别见图1(对应例1)、图2(对应题目1)、图3(对应例2).

图1

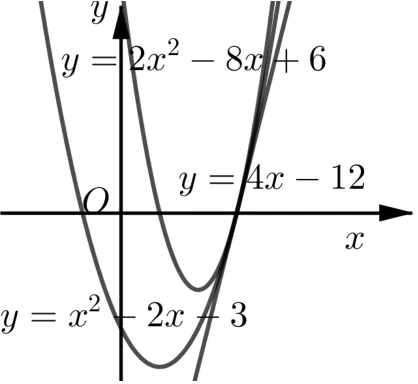
图2

图3

五.典型例题

例1 已知f(x)=ex−1,g(x)=lnx+1 与h(x)=kx+b(k,b∈R)在区间(0,+∞)上恒有f(x)≥h(x)≥g(x),求h(x)的表达式.

解由ex−1≥kx+b≥ lnx+1,令x=1,得1≥k+b≥1,所以k+b=1.设G(x)=ex−1−(kx+b),G′(x)=ex−1−k,满足G(x)≥0=G(1),则由费马引理有G′(1)=0,即1−k=0,所以k=1,b=0.下证充分性.当k=1,b=0,G(x)=ex−1−x,G′(x)=ex−1−1,当x∈(0,1),G′(x)<0; 当x∈(1,+∞),G′(x)>0,所以G(x)≥G(1)=0,所以ex−1≥x.设H(x)=x−(lnx+1),H′(x)=.当x∈(0,1),H′(x)<0;x∈(1,+∞),H′(x)>0,所以H(x)≥H(1)=0,所以x≥lnx+1,所以f(x)≥h(x)≥g(x).因此h(x)=x.

注解题的核心是先观察或分析出是否存在x0使得f(x0)=g(x0).

例2 已知当x≥,−x2+3x−2≤klnx+m≤x−1,求k,m.(答案:k=1,m=0)

例3 (重庆南开中学试题节选)已知f(x)=x2,g(x)=blnx.定义:对于函数f(x)与g(x)定义域上的任意实数x,若存在常数k,m,使得f(x)≥kx+m,g(x)≤kx+m都成立,则称直线y=kx+m为函数数f(x)与g(x)的“隔离直线”.设b=2e,试探究f(x)与g(x)是否存在“隔离直线”?若存在,求出“隔离直线”的方程;若不存在,请说明理由.(答案:存在;y=

解决如例3 这样新定义概念的题型更需要一双“慧眼”.

六.指导意义

三种推广模型及蕴含的思想方法也可以引导我们突破问题.

例4 (2021年八省联考第22题)已知函数f(x)=ex−sinx−cosx,g(x)=ex+sinx+cosx.(1)证明:当时,f(x)≥0.(2)若g(x)≥2+ax,求a.

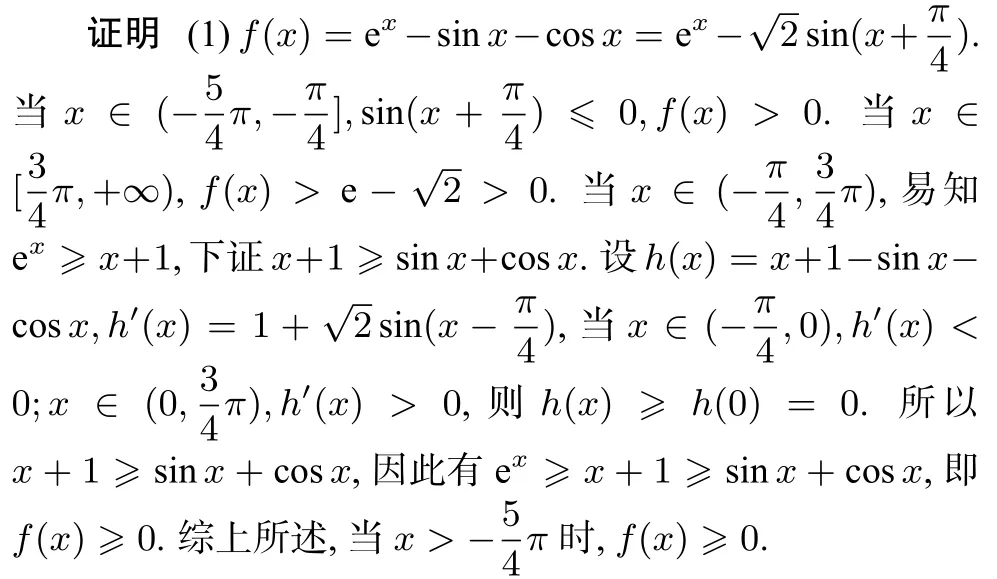
(2)设φ(x)=ex+sinx+cosx−ax−2≥0=φ(0),所以φ′(0)=0,因为φ′(x)=ex+cosx−sinx−a,所以φ′(0)=1+1−0−a=0,即a=2.充分性的证明从略.

思路剖析第(1)问注意到m(x)=ex是凸函数,n(x)=sinx+cosx,n′′(x)=,当x∈,n′′(x)<0,此时n(x)是凹函数.又m(0)=n(0)=1,m′(0)=n′(0)=1,因此m(x)和n(x)在x=0处有公切线y=x+1,故考虑分类讨论:在x∈部分用切线放缩的模型来做,其余两部分根据三角函数值的周期性和有界性去讨论,见图4.第(2)问也用到了观察法和先必要性求值再证明充分性的方法.值得一提的是g(x)和y=2+ax均过(0,2),g′′(x)=ex−sinx−cosx=f(x),由第(1)知当x >−π时,g′′(x)≥0,所以第(2)问的命题有凸函数(局部)的切线放缩的背景.由上述分析也可以对本题做以下改编.

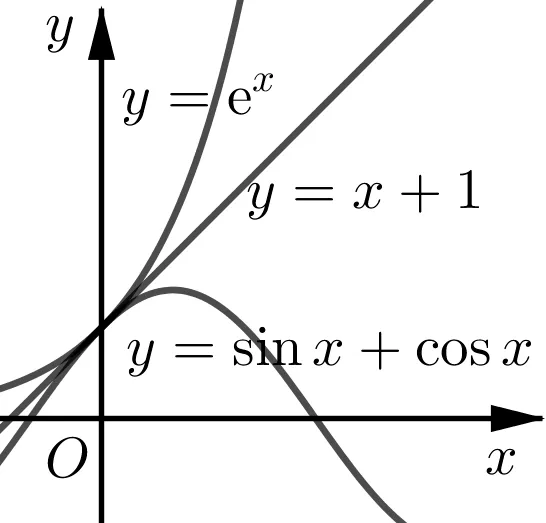
图4

改编题(1)已知:当x∈(−,+∞),有ex≥kx+b≥sinx+cosx成立,求k,b.(答案:k=b=1)

(2)若ex+sinx+cosx≥kx+b≥2 ln(x+1)+2 对任何实数x成立,求k,b.(答案:k=b=2)

注在模型f(x)≥h(x)≥g(x)中,若f(x)恒大于g(x),则上述方法失效,需要分两步f(x)≥h(x),h(x)≥g(x)来做,比如2020年高考江苏卷第19题第(2)(3)问.

众多高考题出题的背景涉及到凹凸函数的切线性质,又因为高中所涉及到的函数一般都具有二阶导数,所以在教学中可以高屋建瓴地适当引导学生通过二阶导数值的正负快速判断函数在某一区间的凹凸性,而一旦具有凹凸性,便可尝试利用其良好的切线性质作为解题的突破口.本文不拘泥于以二次函数为载体,而是对其推广到一般的凹凸函数;推广的模型可以指导解决问题并改编和命制题目(比如例4),体现了创新性.