一类分式求和型数列不等式的多种证明方法

广东省中山市中山纪念中学(528454) 梁世锋

类型一:分式求和型数列不等式

为行文方便,我们首先明确分式求和型数列不等式的概念.称形如(其中r≠0,m,r,s,a,b∈R 且a>0,a≠1)为分式求和型数列不等式.

以下通过证明经典高考试题,给出处理此类问题的典型方法,并说明这些方法在证明中所起的作用.

例1 已知数列{an} 满足:a1=1,an+1=2an+1(n∈N∗).

(1)求数列通项an;(2)证明:

解析(1)由an+1=2an+1 可得:an+1+1=2(an+1),故数列{an+1}是以2 为首项,公比为2 的等比数列,所以an=2n−1(n∈N∗).

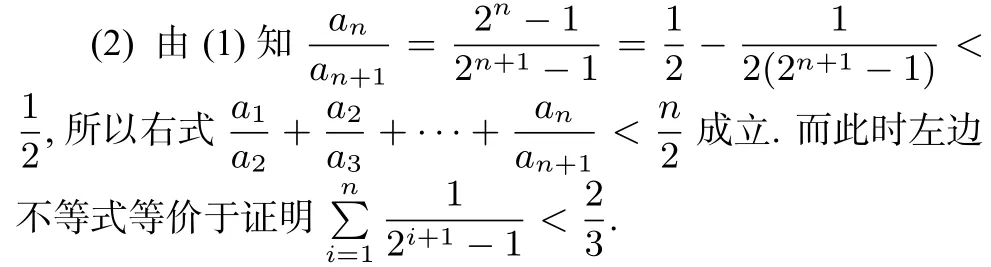
下面用不同方法证明不等式左边成立.

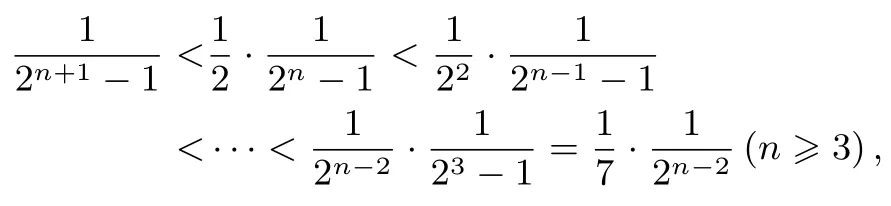
则有

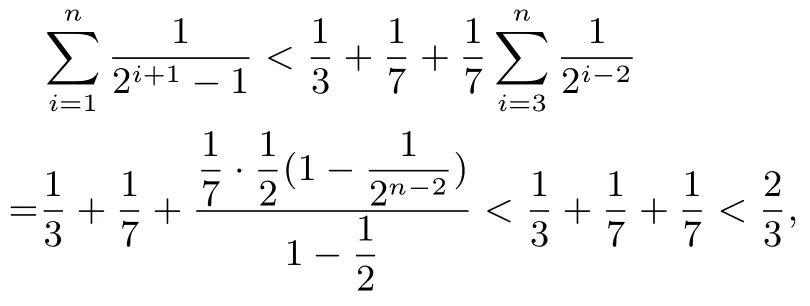
证法5 补项构造裂项相消.

若b<0,则

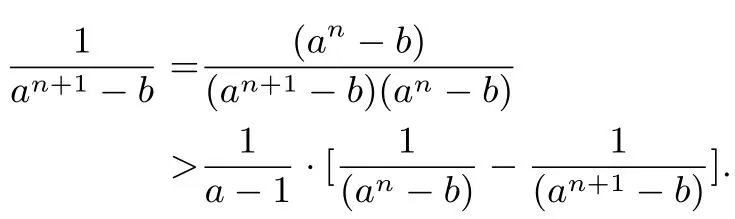
从而实现裂项相消进行放缩,此法的关键在于如下结构:

类型二:分式摆动求和型数列不等式的放缩

例2 已知函数f(x)=,

(1)若数列{an} 满足a1=,an+1=f(an),bn=,n∈N∗,证明数列{bn}是等比数列,并求出的通项公式;

解(1)bn=2n(n∈N+),过程从略.

证法1 奇偶并项,构造等比数列.

(2)当n为偶数时,

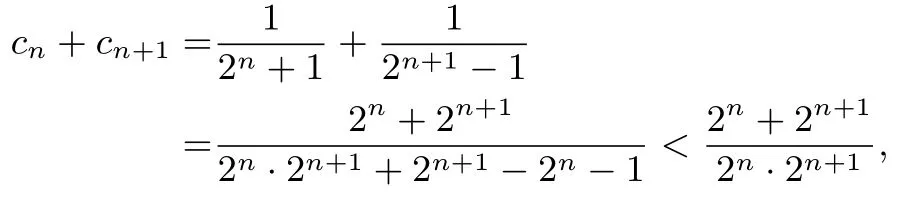
即cn+cn+1<.所以

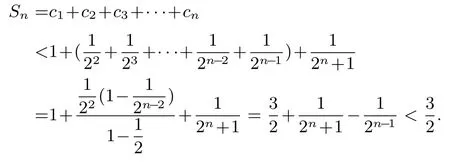
当n为奇数时,则n+1 为偶数,由上知:

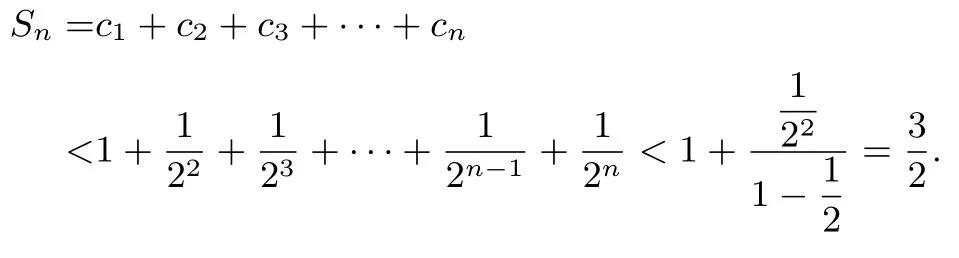
证法2 避开并项求和,构造等比数列.

类似地,参照类型一的方法,可以构造

成立,同样保持前两项不变,从第三项起进行放缩,从而

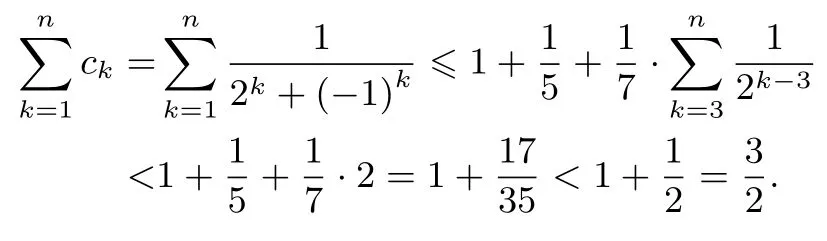
类型三:分式求积型数列不等式放缩

例3 (2006年高考江西卷)已知数列{an}满足:a1=,且an=(n≥2,n∈N∗),

(1)求数列{an}的通项公式;

(2)证明:对于一切正整数n,不等式a1·a2·a3···an <2n!

证法二据(1)得,

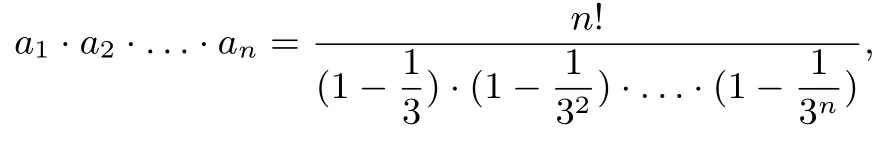
为证:a1·a2·a3·...·an <2n!,只要证n∈N∗时有

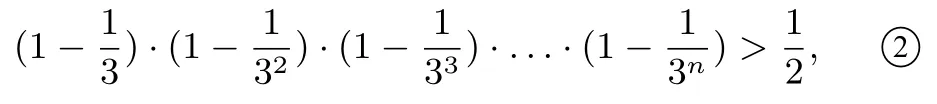
显然,左端每个因式都是正数,先证明,对每个n∈N∗,有

(此处隐含不等式(1−x)·(1−x2)·(1−x3)·...·(1−xn)≥1−(x+x2+x3+···+xn)x∈(0,1)成立.)

用数学归纳法证明③式:

(1)n=1 时,③式显然成立,

(2)设n=k时,

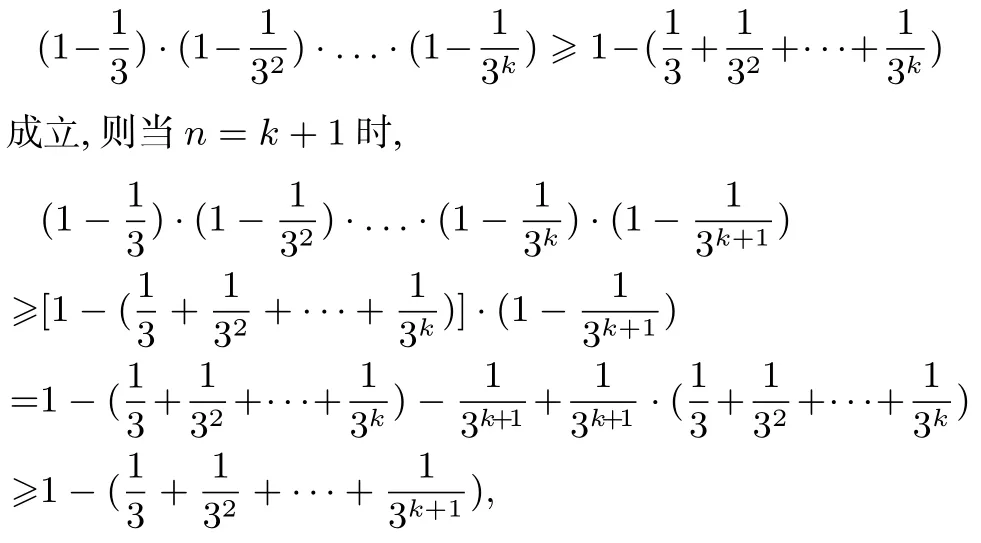
即当n=k+1 时,③式也成立.故对一切n∈N∗,③式都成立.利用③得,

所以故②式成立,从而结论成立.