基于倒装键合设备的准直调平系统研究
2022-07-15郝耀武王增琴
闫 瑛,郝耀武,王增琴
(中国电子科技集团公司第二研究所,山西 太原030024)
随着半导体制造工艺的进步和市场对微小芯片需求的急速增长,芯片I/O密度越来越高,芯片尺寸、芯片引线键合和焊盘直径持续减小,因而对封装设备的键合精度提出了极高的要求[1],键合前相对平行度的好坏直接决定了键合精度的稳定性,键合过程如图1所示。目前主要依靠机械装调或自适应的方式来保证键合前的平行度,但对于凸点倒装,机械装调的效果和自适应无法满足高精度键合的需求。因此,准直调平系统的研制对于高精度倒装芯片的互连有重大意义。

图1 倒装键合过程示意图
1 自准直原理
数字光电自准直仪原理如图2所示,光线通过位于物镜焦平面的分划板后,经物镜形成平行光。平行光被垂直于光轴的反射镜反射回来,再次通过准直镜头后由分光棱镜转折汇聚在位于共轭焦平面的CCD表面,形成分划板像。当反射镜倾斜一个微小角度时,反射回来的光束就产生一个倾角,位于CCD探测表面的分划板像就产生一个位移。通过CCD对分划板像位移的判读即可得知反射镜的角位移。这就是光学自准直的基本原理。设分划板到物镜的距离为f,反射镜偏转角度为α,十字分划板在CCD上所成像的位置变化为γ,则α=γ/2f。

图2 数字光电自准直仪原理图
2 准直光路设计
根据光学自准直原理及倒装工艺需求设计准直系统,设计平面图[2]如图3所示。
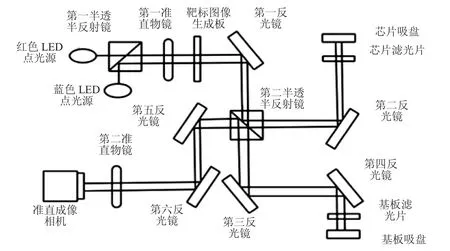
图3 准直光路设计平面图
3 准直系统光学设计及像质评价
准直系统的设计,主要考虑矫正球差、彗差、畸变等,设计结果如图4所示。

图4 准直系统光学设计图
对准直系统的光学设计结果进行综合模拟及仿真分析与计算。光学系统MTF如图5所示,能量集中度曲线如图6所示,畸变曲线如图7所示。
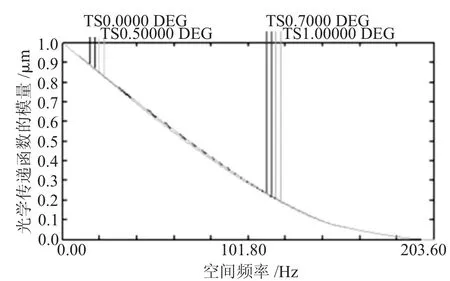
图5 准直系统MTF曲线

图6 准直系统能量集中度曲线
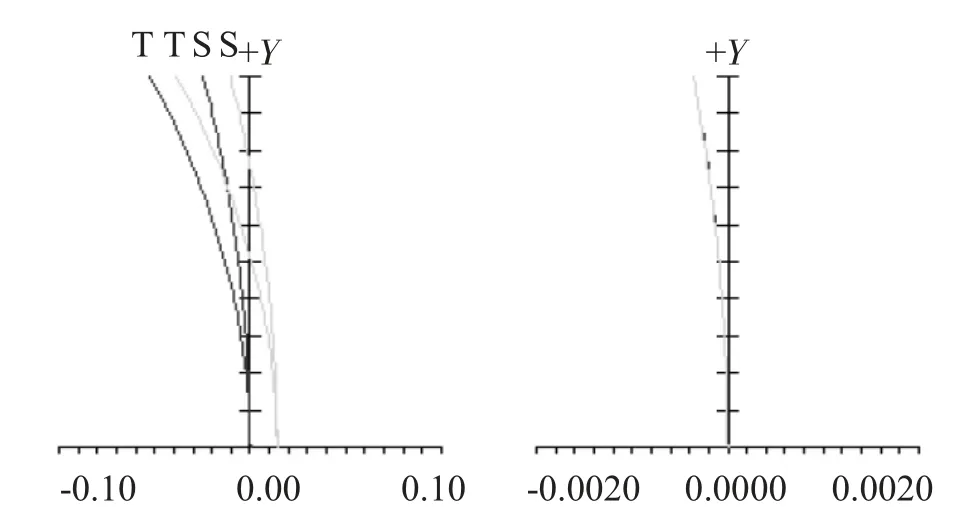
图7 准直系统畸变曲线对比
根据以上仿真与分析可知,系统在可见光波段全视场MTF已设计为衍射极限系统,系统的弥散圆半径都在1μm以内,系统成像质量很好,能够满足对十字分划板成清晰的图像。
另外,透过系统畸变曲线可知,本系统畸变的最终设计值为0.000 32%,可以保证十字分划像不变形。
4 准直调平过程设计
准直系统的工作原理如图8所示,分别将十字靶标图形如图9所示投射在芯片和基板的反射面上,图形反射通过准直光路投射到CCD上。根据光学准直原理,假如CCD上显示两个不重合的十字靶标,则认为芯片和基板两平面不平行,通过驱动平行度调节执行机构,调节两个十字靶标到完全重合,则完成芯片和基板的平行度调节。

图8 准直系统工作原理图
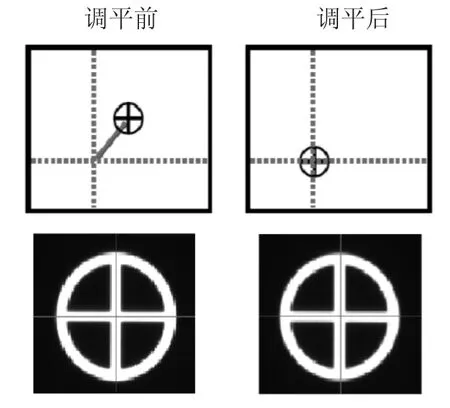
图9 十字靶标
调节过程中通过视觉拍摄上下两个十字靶标图形在视场坐标系内的位置坐标,以基板靶标为基准,可以计算出两靶标之间的XY方向像素坐标的偏差值(rx,ry),依据激光干涉仪已经标定的位移与脉冲对应关系(在整个行程中分别记录多组XY方向脉冲与对应像素坐标的值,采用Matlab中最小二乘法进行拟合,计算出两组像素和脉冲的对应关系),分别计算像素偏差对应的脉冲量,调节对应的步进电机,实现调平功能。
高精度机构采用半球气浮结构,分别通过驱动俯仰和偏摆电机推动精密螺旋推杆,使球凸产生两个方向的运动,设计原理为:已知步进电机推杆和球面连接杆交点到球面定点的距离为A,如图10所示,球面半径为R,转角分辨率为B,转角行程为C,步进电机导程为S,传动装置的综合传动效率为η,减速比为i,保持转矩为HT,设:D为步进电机脉冲行程,θS为步进电机步距角,E为整个行程允许位移,F为推力[3],计算过程如下:

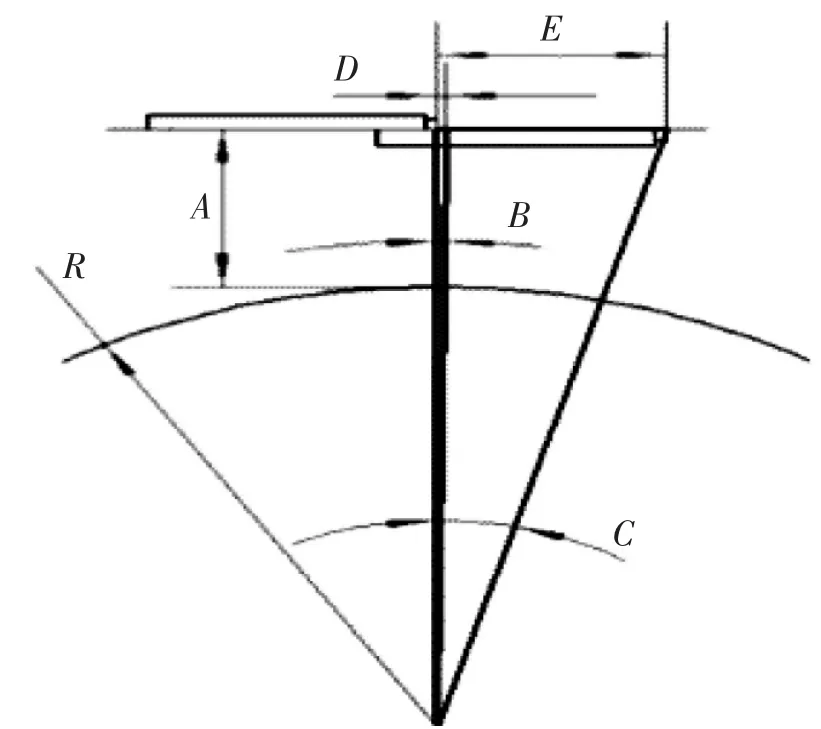
图10 半球气浮结构示意图
5 结束语
本文从高精度倒装键合工艺需求出发,提出了基于自准直原理的调平方案,给出了相应的光路设计以及仿真过程,配合视觉检测以及高精度执行机构实现准直调平的功能,目前准直调平功能以及在高精度倒装设备上进行了验证,功能和性能均能满足设备使用要求。
