面向区域导航增强的低轨卫星星座设计
2022-07-15靳云迪林静然邵怀宗
陈 林,李 楷,靳云迪,林静然,3*,邵怀宗,3
(1. 中国电子科技集团公司第二十九研究所 成都 610036;2. 电子科技大学信息与通信工程学院 成都 611731;3. 鹏城实验室 广东 深圳 518055)
近年来,全球卫星导航系统日趋完善,应用不断拓展,在各领域为用户提供高质量的定位、导航和授时服务[1]。另一方面,现有导航卫星大多部署在中高轨道,给导航服务质量带来不利因素。如卫星运行在较高轨道时,空间几何构型短时间不会显著变化,导致精密单点定位收敛时间较长[2-3];此外,高运行轨道必然引起传输链路的长时延和高损耗,导致接收端信号微弱且容易受到干扰和欺骗,影响服务性能等。
针对上述问题,研究人员提出了部署低轨卫星的解决方案并受到广泛关注[4]。低轨卫星星座的空间几何构型变化快,能够辅助提升定位收敛时间及定位精度[5-6];由于传输距离更短,低轨卫星播发的导航信号在接收端质量更好,能够大幅提升导航信号的精度和覆盖能力。目前,低轨卫星是对现有卫星导航系统的有效补充,是实现导航增强的重要手段。
在低轨卫星的部署过程中,采用何种星座构型是影响其覆盖能力和导航增强效能的重要因素。针对全球覆盖的要求,文献[7-9]归纳分析了低轨卫星轨道设计的主要准则和权衡策略。文献[7]给 出 了 一 种 几 何 精 度 因 子(geometric dilution of precision, GDOP)和全球可见星数量均匀分布的星座设计方案;文献[8]将常见低轨卫星星座方案与北斗3 号系统(BeiDou-3 system, BDS-3)结合,针对位置精度因子和全球可见星数量进行了分析对比,论证了低轨卫星对BDS-3 系统的增强效果;文献[10]分析了“鸿雁”低轨星座对现有导航系统在GDOP 和精密单点定位首次收敛时间等方面的增强效果。
上述关于低轨卫星星座设计的研究都是针对全球导航增强的需求,主要采用了基于近圆形轨道的星座构型。另一方面,出于部署难度、成本以及应用场景的考虑,很多时候需要研究如何部署低轨卫星对局部重点区域进行导航增强。针对该问题,文献[11]设计了一种由256 颗低轨近圆形轨道卫星组成的Flower 星座构型方案。该方案仍然使用近圆形轨道,卫星对轨道下的所有区域有着几乎相同的覆盖和导航增强效能,当对覆盖和导航增强的需求有区域限制时,这种无区别覆盖的方案难以达到最优效率。与近圆形轨道不同,椭圆轨道更适合于实现局部区域的覆盖。文献[12]引入了回归系数,可以定量地计算椭圆卫星轨道。文献[13]给出了一种限制椭圆轨道远地点的星下点与目标点重叠的星座设计方法,验证了椭圆轨道星座对特定区域的覆盖性能优于近圆轨道星座。但是,该方案只保证了最初始设计的那颗卫星的远地点限制条件,不能保证同一轨道面的所有卫星在远地点时都能经过目标点上空,仍然会造成观测时间和空间上的浪费。
在上述研究基础上,本文提出了一种新型的面向区域导航增强的低轨卫星星座方案,和现有方案相比,在低轨卫星数量相同时,能够有效提升覆盖重数、过顶时间、GDOP 等影响导航性能的关键指标,具有更好的导航增强效果。
为了更清楚地说明本文讨论的低轨区域导航增强星座的作用与必要性,将其与北斗2 号(BDS-2)区域导航星座[14]进行比较。BDS-2 采用地球静止轨道(geostationary earth orbit, GEO)卫星、倾斜地球同步轨道(inclined geosynchronous orbit, IGSO)卫星、与中圆地球轨道(medium earth orbit, MEO)卫星实现对亚太地区的覆盖。由于采用中高轨卫星,存在卫星运动动态小,精密单点定位过程中载波整周解模糊过程收敛时间长,卫星轨道高,需要大功率发射机才能保证信号落地电平等不足。本文的低轨局部星座与BDS-2 星座主要异同如下:
1) 二者都是利用卫星广播导航信号,在用户容量上不受限。
2) BDS-2 采用近圆形轨道,本文采用椭圆形轨道。椭圆形轨道能够显著增大设定区域的过顶时间;另一方面,卫星在椭圆轨道中运行受地球摄动影响较大,轨道预报难度提高,轨道预报精度相比圆轨道略差,同时,在椭圆轨道运行时,卫星离地表距离变化较大,地面接收信号动态大,需要接收机具有较大的信号接收动态范围。
3) BDS-2 是针对亚太地区设计的独立导航系统,其位于中高轨,单星一般在1 000 kg 量级,且星座和卫星均独立设计、独立运行。
4) 本文利用低轨星座配合现有全球导航系统,实现局部导航增强,理论上可以针对任意区域进行导航增强,且通过较少卫星数量和单星就可达到目的,单星一般在100 kg 量级,同时具有易于和通信卫星一体化设计等优点。
1 北斗三号的经典低轨导航增强星座
本文以BDS-3 全球导航系统为对象研究面向区域导航增强的低轨卫星星座设计。如表1 所示,BDS-3 系统标称空间星座由3 颗GEO卫星、3 颗IGSO 卫星、24 颗MEO 卫星组成[15]。针对BDS-3 系统的导航增强问题,文献[16]给出了一种GDOP 极小化的Walker 组合构型计算方法,即:
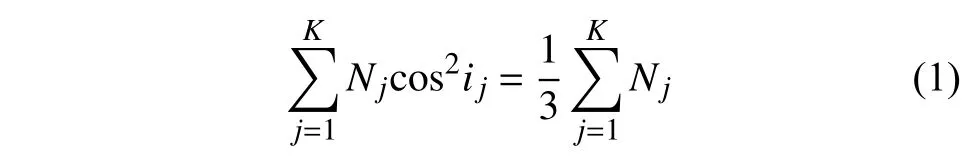
式中,Nj为第j个单Walker 构型的卫星数;K为构型数量;ij为第j个单Walker 构型的轨道倾角。常见的设置是K=2,即两种倾角的Walker 构型组合。如表1 所示,一个为倾角45°、48 颗星的Walker 星座;另一个为倾角为75°、30 颗星的Walker 星座。
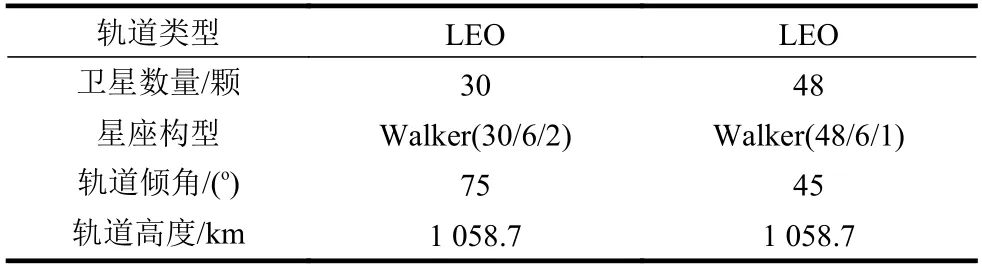
表1 GDOP 极小化的导航增强低轨星座
表1 中的低轨导航增强星座采用近圆形轨道,且Walker 构型星座在空间上均匀分布,此类星座对南北半球有对称的观测效果,当要求覆盖区域范围较小时会造成观测空间和时间的浪费。基于以上考虑,本文引入椭圆轨道,利用其远地点特性,使其覆盖重心聚焦在需要导航增强的局部区域。
2 区域导航增强低轨卫星星座设计
2.1 低轨星座设计思路
参考文献[12-13]中的椭圆轨道设计流程,结合区域导航增强需求,对星座设计流程进行改进,使其聚焦在需要增强的区域,在部署相同数量的低轨卫星时,达到更好的导航增强效果。
现有椭圆轨道设计流程主要满足轨道远地点与增强区域相对应这一基本要求,并未从细节上考虑如何尽可能地优化导航增强性能。如现有设计流程往往只保证最初始设计卫星的远地点限制条件,由于地球自转、轨道回归特性等因素的影响,难以保证其余卫星的星下点轨迹也能经过目标区域中心点,这给区域覆盖和导航增强性能带来损失。
基于上述分析,考虑Flower 星座构型[17],它是由一组共地面轨迹[18-19]的卫星构成的星座。利用该特性进行低轨卫星椭圆轨道设计,获得的星座也具有共地面轨迹特性,能够提升导航增强性能。
2.2 低轨卫星星座设计流程
卫星椭圆轨道运动可用开普勒参数来描述,包括:轨道升交点赤经Ω(或升交点经度λ0)、轨道倾角i、近地点幅角ω、长半径a、偏心率e和卫星的真近点角v。围绕这6 个参数,面向区域导航增强的椭圆轨道低轨卫星星座设计流程如下。
1) 确定目标点经纬度(λ, φ)和轨道倾角i。一般选取导航增强区域的中心点为目标点。轨道倾角主要影响覆盖的纬度范围[8],根据区域的纬度跨度确定,也可根据特定的需求确定,如临界轨道等。
2) 确定近地点幅角ω 和真近点角v。当目标点纬度φ、轨道倾角i和近地点幅角ω 满足:

可以保证卫星过远地点时刻位于目标点上空。真近点角v为:

3) 确定回归系数Q。回归系数是描述轨道回归特性的参数,回归轨道是指星下点轨迹经过一段时间后重复出现的轨道。根据轨道高度所处的范围,结合式(3),中长半轴与偏心率的关系为:

式中,ha和hp分别为椭圆轨道的远地点和近地点高度;Re为地球平均半径。将相关参数范围带入式(5),可计算Q的范围:
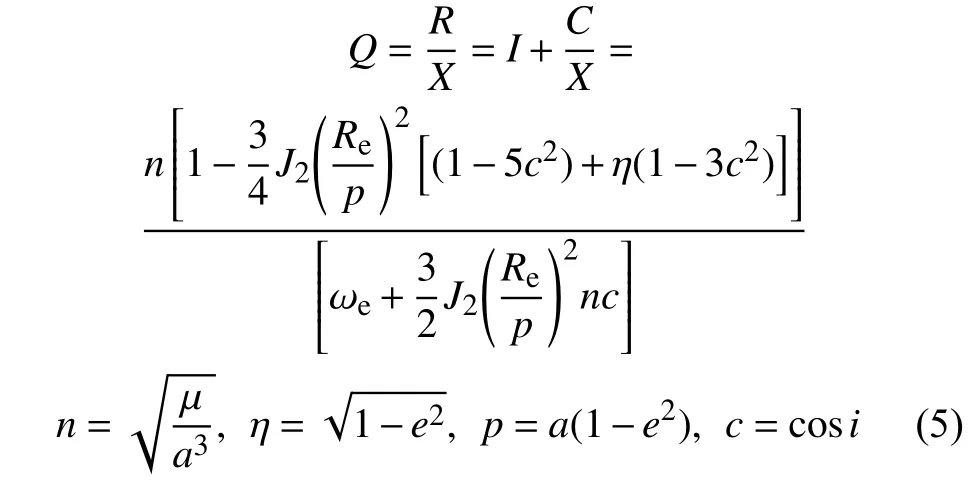
式中,µ为地球引力常数;J2=0.001 082 63 为地球引力带二阶谐项系数;ωe为地球自转角速度;回归系数Q由整数部分I和真分数部分C/X组成;I、C、X均为正整数,C与X互质。式(5)中的回归系数Q表示卫星在X天运行R圈后完成一次回归。
在轨道设计过程中,远地点高度ha主要限制卫星在远地点时的覆盖范围。回归系数Q可参考卫星的重访特性选择,根据文献[20]的结论,一般选取回归天数较小、回归圈数较大所对应的Q值。
4) 确定长半轴a和偏心率e。将流程3)选定的回归系数Q和近地点高度hp重新代入式(4)和式(5),可确定远地点高度ha,并得到轨道长半轴a和偏心率e。
5) 确定升交点经度λ0。根据目标点经度λ,轨道倾角i和真近点角v,利用式(6)可以计算升交点经度λ0和偏近点角E:

6) 构建星座。首先,利用式(7)计算初始卫星的平近点角M0:
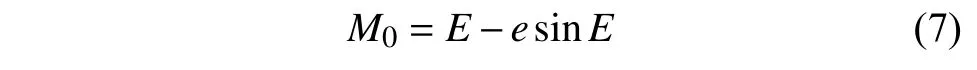
然后,设定Flower 星座的每个轨道面卫星数等于回归天数X。基于初始卫星的升交点经度λ0和平近点角M0,均匀分布的Flower 星座相邻轨道面的升交点赤经差Δλ 和每颗卫星的平近点角M(m,n)计算如下:

式中,P为轨道面数;X为回归天数;m=0,1,···,P−1,为轨道面编号;n=0,1,···,X−1,为轨道面内卫星编号。
3 低轨卫星星座设计实例
设计一个低轨卫星星座对我国中西部地区进行导航增强,区域中心点位于(30.666 7°N, 104.067°E),区域经纬度跨度均为20°。
3.1 临界轨道参数
基于临界轨道方案确定轨道倾角i,以避免轨道平面拱线漂移。考虑地球引力位函数对卫星轨道的摄动时,近地点幅角、偏心率的变化率分别为[21]:


令各变化率为零,求得临界轨道倾角为i=63.43°。
3.2 椭圆卫星轨道高度限制
由于范·艾伦带中的高能粒子穿透力强,对星载电子设备的损害极大,在设计卫星轨道高度时应避开范·艾伦带的内带(1 500~8 000 km)和外带(15 000~25 000 km)。选取椭圆轨道近地点高度hp=1 000 km,位于内带以下;远地点高度位于内外带之间,即8 000~15 000 km 范围内。
3.3 星座设计结果
1) 选取临界轨道倾角i=63.43°;
2) 根据导航增强区域中心点的经纬度坐标,即(30.666 7°N, 104.067°E),由式(2)计算出近地点幅角ω=214.769°,由式(3)计算出真近点角v=145.231°;
3) 远地点高度范围为8 000~15 000 km,由式(4)和式(5)计算回归系数Q的范围[5.015 2, 7.612 0],由于Q取7 时远地点高度降低过多,影响覆盖性能,选取Q=6,即卫星运行6 圈后回归,回归周期为1 天。
4) 根据回归系数Q和近地点高度ha的值,利用式(5)确定远地点高度hp=11 754 km,再利用式(4)可得长半轴a=12 755 km,偏心率e=0.421 5。
5) 直接将相关参数带入式(6),计算出升交点经度为λ0=98.83°和偏近点角E=127.72°。
6) 计算初始卫星的平近点角M0=108.61°,在Flower 星座框架下,选择P=9 个轨道面,每个轨道面的卫星数为X=1 颗。利用式(8)可得相邻轨道面升交点经度差为40°,初始卫星平近点角差− 240◦。
由此完成了面向区域导航增强的低轨卫星星座设计,其主要参数如表2 所示。

表2 面向区域导航增强的低轨卫星星座
关于星座设计的结果有两点需要说明。
1) 椭圆轨道高度的选择是多个因素综合考虑折中的结果。一般而言,轨道高度越低,在载波快速收敛、地面信号强度方面的增强效果越好;但同时单星覆盖范围也越小,覆盖相同区域需要的卫星数也越多。本文在选择轨道高度时,综合考虑了导航增强效果和单星覆盖区域,同时尽量避开了对卫星寿命损害极大的范·艾伦带。基于上述考虑,本文设计在增强效果、卫星数量和卫星寿命方面进行了折中,椭圆轨道远地点高度为11 754 km。根据电波在自由空间传输的损耗模型[22]:
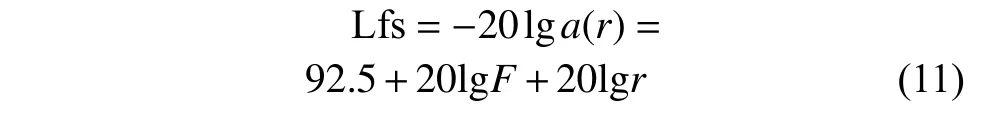
式中,F为载频,单位为GHz;r表示传播距离,单位为km。在传输距离损耗方面,椭圆轨道远地点信号传输损耗为81.4 dB,与之相对,BDS-3 的GEO/IGSO 卫星轨道高度为35 786 km,对应的传输损耗为91.1 dB;MEO 卫星轨道高度为21 528 km,传输损耗为86.7 dB。由此可见,如果星上发射功率相同,在地面用户端低轨卫星的信号强度最高有10 dB 提升。
2) 本文设计方案具有通用性,当重点区域的位置发生变化后,利用本文的星座设计方法可以快速计算出新的低轨卫星星座参数。至于实际星座调整过程中涉及到的指令发送、姿态控制、变速变轨等操作的原理和具体实施过程,则不在本文讨论的范围内。
4 低轨星座区域导航增强效能分析
利用覆盖重数(可见星个数)、过顶时间、GDOP等指标验证本文设计的低轨卫星星座在区域导航增强上的性能优势。覆盖重数和GDOP 的仿真软件为MATLAB,过顶时间的仿真软件为STK。
4.1 共地面轨迹设计的区域覆盖性能优势
通过覆盖重数和过顶时间验证星座设计中的共地面轨迹条件带来的覆盖优势。为便于对比,在低轨卫星数量不变的条件下,设计了基于经典Walker构型的椭圆轨道星座,它具有3 个均匀分布的轨道面,每个轨道面有3 颗卫星,真近点角分别为145.231°、202.556°和329.725°,其他椭圆轨道参数不变。在给定区域上对两种星座的覆盖重数和过顶时间进行仿真。仿真开始时刻为世界协调时2020 年5 月15 日4 时,最低仰角设为5°。
覆盖重数仿真时长48 h,步进为300 s。图1为两种星座的全球平均覆盖重数分布情况,图中虚线框表示以目标点为中心、经纬度跨度为20°构成的区域。图1a 和图1b 分别为经典Walker 星座和本文设计星座的全球覆盖重数,可以发现,Walker星座的覆盖特性在经度上比较均匀,而本文设计星座则呈现出明显的区域覆盖特性。图1c 给出了在设定区域上,本文设计星座相对于Walker 星座在覆盖重数上的提升,说明在给定区域上,本文设计星座的覆盖重数都高于经典Walker 星座。
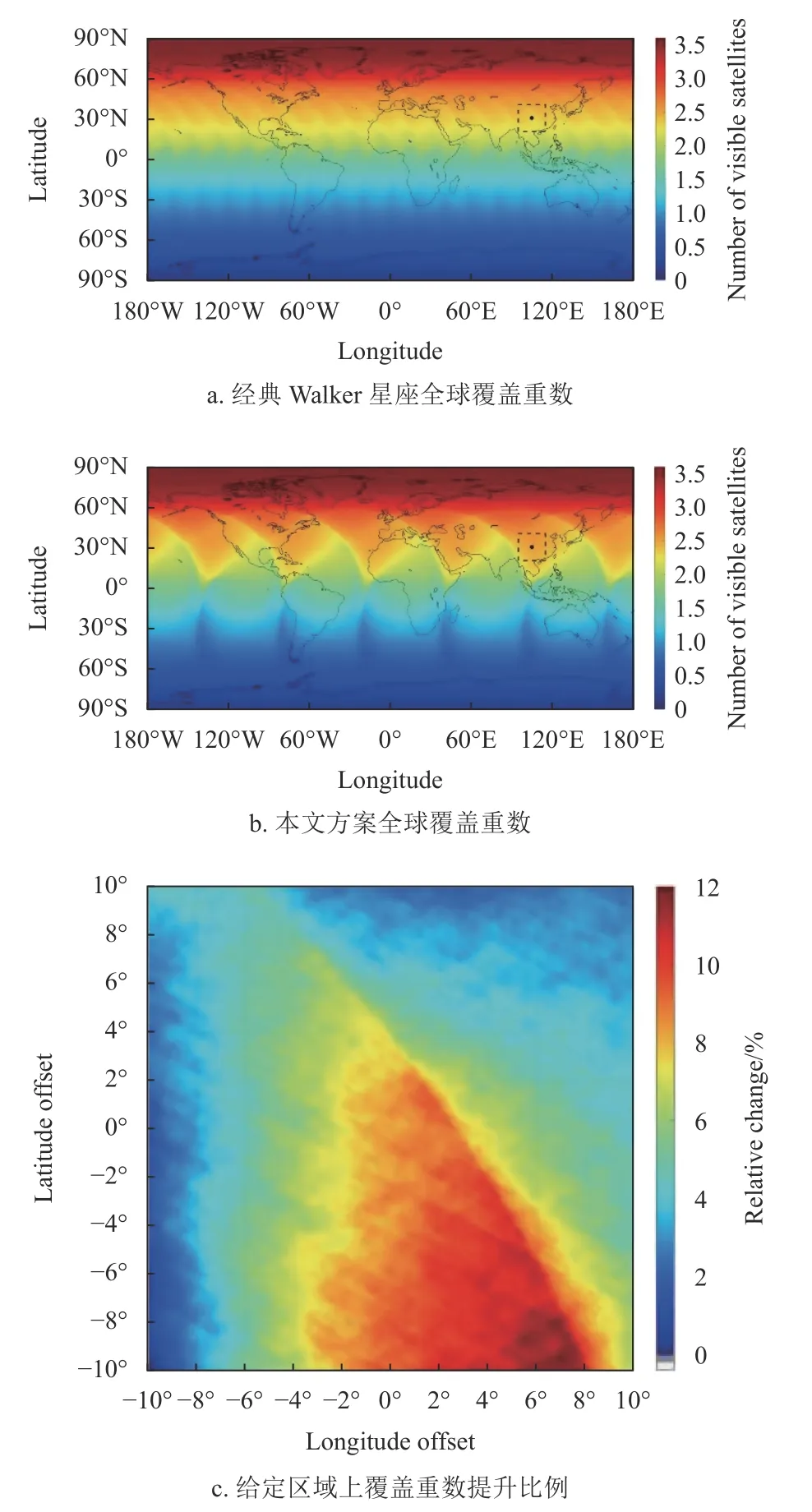
图1 两种低轨星座的覆盖重数对比
表3 为两种星座对区域中心点的过顶时间对比。本文的星座在平均过顶时间和过顶时间占比方面都优于经典Walker 星座,且过顶时间更为稳定和集中。
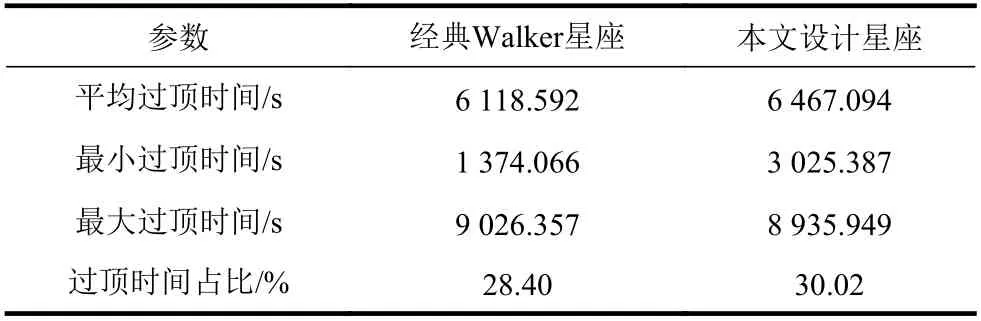
表3 过顶时间对比
4.2 椭圆轨道设计的区域覆盖性能优势
为了验证椭圆轨道方案的优势,将其与近圆形轨道方案对比。在面向全球导航增强的经典近圆形轨道Walker 星座基础上,进一步增加本文设计的椭圆轨道星座进行辅助。具体而言,选取两种Walker 星座,分别为表1 中由78 颗低轨卫星构成的星座,即Walker 30/6/2(75°)+Walker 48/6/1(45°)和由116 颗低轨卫星构成的Walker 星座,即
Walker 36/6/2(75°)+Walker 80/8/1(45°)。
图2 为在78 星Walker 星座上叠加本文设计的星座后,在给定区域上相对于78 星Walker 星座和116 星Walker 星座的覆盖重数提升情况,结果验证了椭圆轨道低轨星座在区域导航增强方面的高效性:在78 星近圆形轨道Walker 星座上叠加本文设计的9 星椭圆轨道星座,就能达到与116 星近圆形轨道Walker 星座等同的区域导航增强效果。
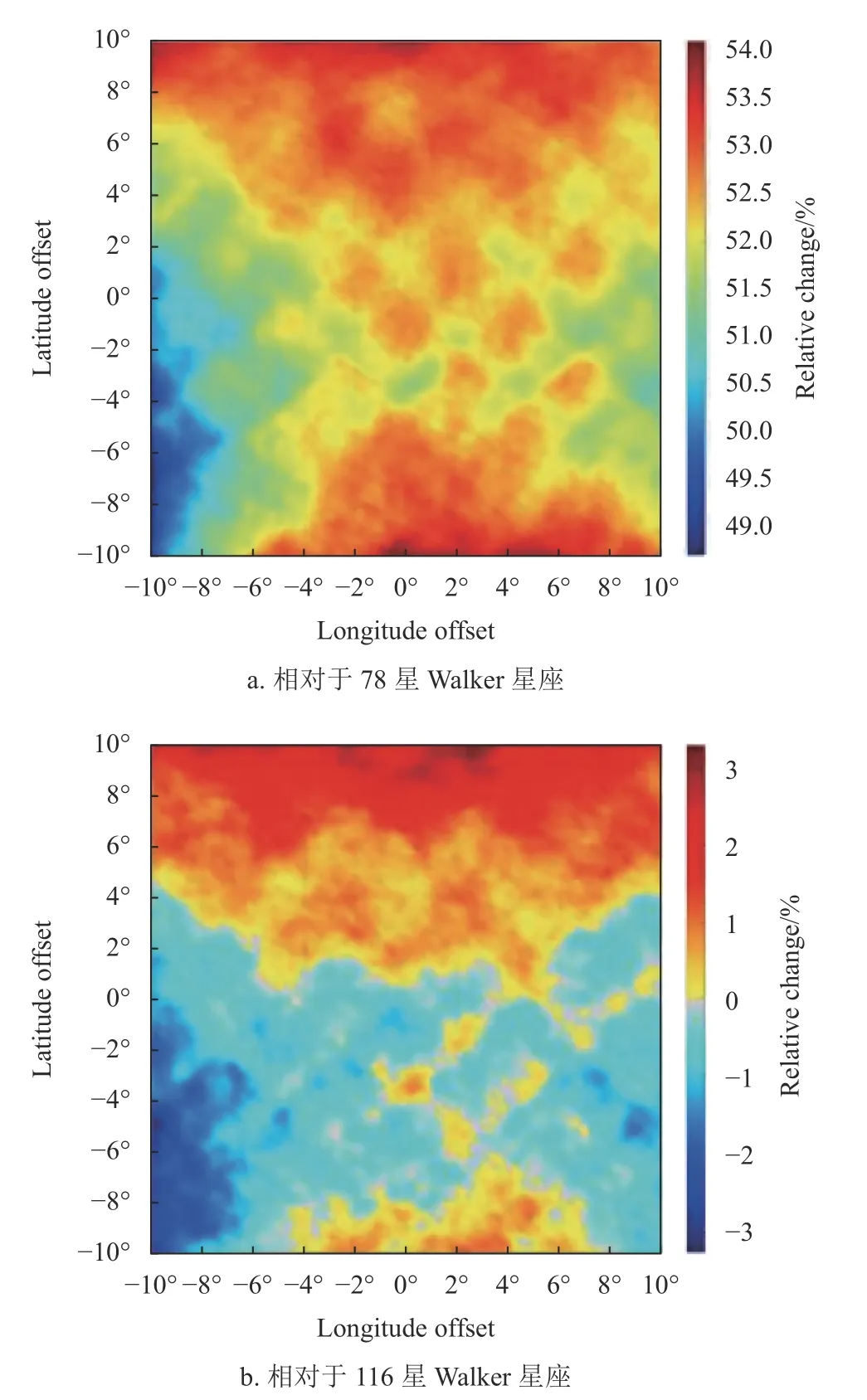
图2 叠加本文设计低轨星座后区域覆盖重数提升情况
最后,结合BDS-3 系统,对比本文椭圆轨道低轨星座和其他相关星座在给定区域上的GDOP。同样部署相同数量的低轨卫星,即在表1中78 星近圆形轨道Walker 星座上分别叠加4.1 节中两种9 星椭圆轨道星座。图3a 在全球范围内的经、纬两个维度上对比了上述两种星座的GDOP。本文星座设计方案联合考虑了椭圆轨道和共地面轨迹两个条件,在关注的重点区域,无论是经度维度还是纬度维度,本文方法都具有更低的GDOP,表明在给定区域内星座空间构型更好,定位导航精度更高,达到了区域导航增强的目标。关注区域之外的GDOP 对比情况,不是本文关注的重点(本文研究的应用场景为区域导航增强、而非全球导航增强)。如果关注的区域发生了变化,则需要更新区域信息,重新计算新的低轨卫星星座。另一方面,从图中可以看出,相对于经典Walker 星座,本文低轨星座在经纬度上的GDOP 增强效果并不均匀。经度方面,重点区域中心增强效果最好,两侧的增强效果逐渐减弱;纬度方面,低纬度区域的增强效果优于高纬度区域。图3b 从二维平面上给出重点区域内的GDOP增强情况,结果与上面的分析一致。在重点区域的下边界中心,增强效果最明显,GDOP 值相对降低达2.5%;重点区域右上角的增强效果最弱,GDOP 值降低0.5%。这种增强效果不均匀的现象是由椭圆轨道形状、近地点远地点高度限制、重点区域的选取、地表曲率等多种因素造成的,同时也与星座设计方案需要兼顾覆盖重数、过顶时间、GDOP 等多方面的导航增强需求有关。尽管存在增强效果不均匀的情况,但在整个区域内GDOP 值都有所减小,不同程度地提高了导航定位精度。
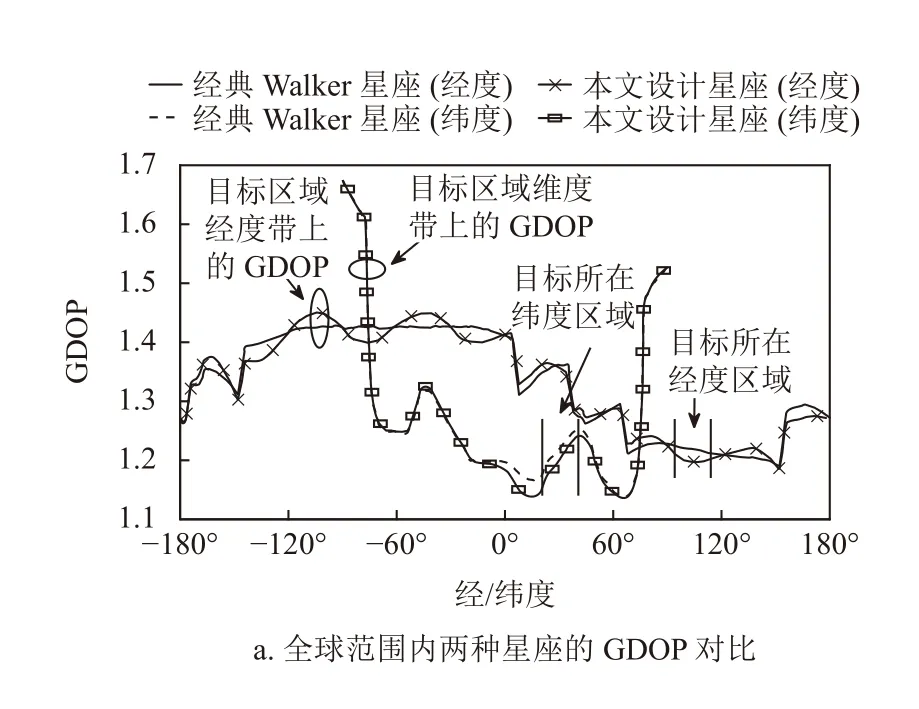
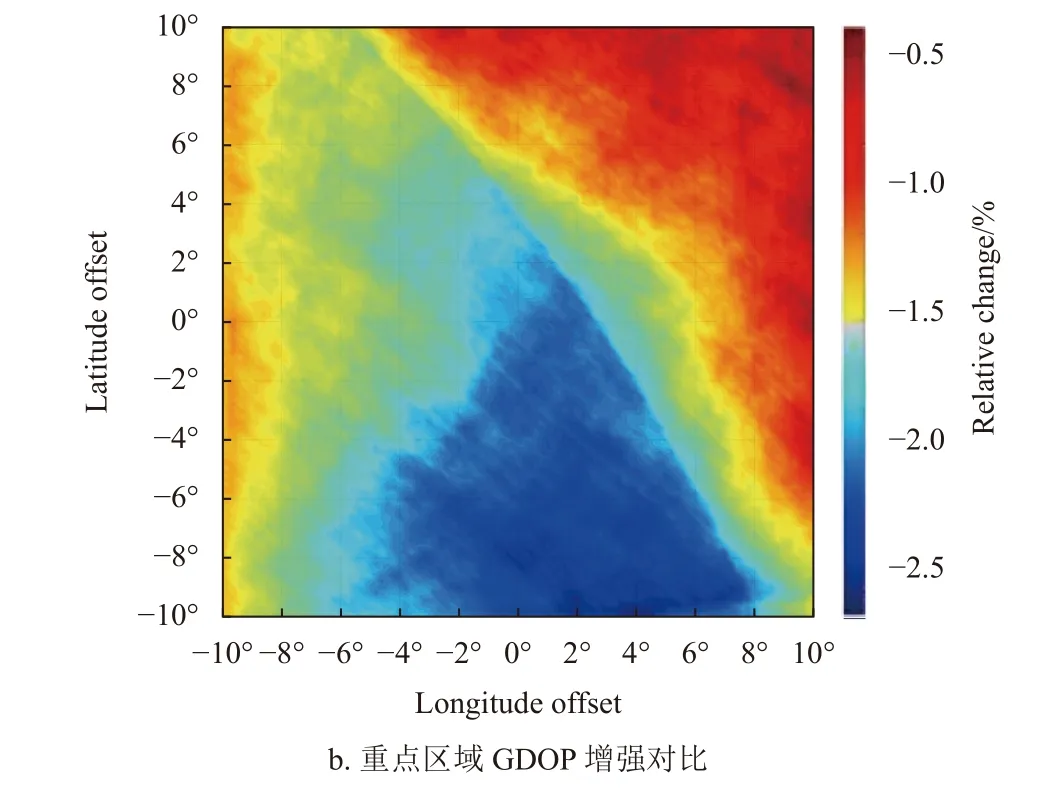
图3 低轨星座在GDOP 方面的增强效果
5 结 束 语
本文提出了一种面向区域导航增强的低轨卫星星座设计方法,该方法聚焦区域导航增强的需求,采用了椭圆轨道方案,并且在具体轨道参数设计时,采用了共地面轨迹设计思路。与相关的低轨星座设计方法相比,在部署相同数量的低轨卫星时,本文方法能够显著改善给定区域内的卫星覆盖重数、过顶时间、GDOP 等影响导航性能的关键指标,达到更好的导航增强效果。
