基于SURE 准则的参数自适应InSAR 相位非局部滤波

高雨欣，郭 睿，王 辉，张双喜

（1.西北工业大学 电子信息学院，陕西 西安 710129；2.西北工业大学 自动化学院，陕西 西安 710129；3.上海卫星工程研究所，上海 201109）

0 引言

干涉合成孔径雷达（Interferometric Synthetic Aperture Radar，InSAR）通过对同一地区获取的两幅或多幅相干图像进行干涉处理获取高精度的地面高程信息，在地形测绘、地表变形监测、土地覆盖分类、目标监测、宽幅场景测速等遥感领域发挥着重要作用。在InSAR 数据处理过程中，干涉相位滤波是减少由热噪声、不同去相关和SAR图像配准引入噪声的基本步骤。因此，先进的相位滤波方法成为了干涉处理中获得高质量干涉图的必须研究课题之一。

非局部滤波器可以有效地捕捉相位结构，尤其在条纹滤波和细节保持方面表现优异，其在InSAR相位去噪中的应用引起了学者们极大的关注。DELEDALLE 等提出了一种基于幅度、相干系数和干涉相位联合统计分布的非局部干涉相位估计方法。SICA 等将基于非局部方法的块匹配3-D（The Block-Matching 3-D，BM3D）算法扩展到InSAR 相位恢复领域。为进一步改进非局部均值滤波器的滤波结果，Stein 的无偏风险估计（Stein’s Unbiased Risk Estimate，SURE）准则被引入非局部均值滤波。YANG 等提出了一种基于统计特性非局部均值和鲁棒双边滤波器的混合算法，该算法使用SURE准则估计最优参数。LI 等提出了一种基于变分贝叶斯推理和SURE 准则的联合非局部去噪方法。目前关于SURE 准则下非局部滤波在实测InSAR 干涉相位数据的噪声抑制中的有效性研究较少。

基于此，提出了一种基于SURE 准则的非局部均值滤波器自适应参数选择方法，并应用于大场景下的InSAR 实测数据。首先，简要回顾了非局部均值算法和SURE 准则在非局部均值滤波器上的应用；然后，着重介绍了应用于InSAR 实测数据相位滤波的SURE 准则参数自适应非局部均值滤波器；最后，通过仿真数据和实测数据评估了所提出方法的有效性，并将结果与其他2 种广泛使用的滤波器进行了比较。

1 理论背景

1.1 非局部均值算法

含噪图像可以描述为

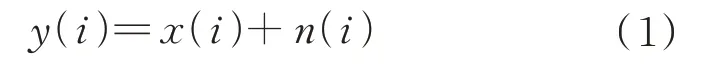
式中：（）、（）分别为实测图像和原始图像中的第个像素；为方差为σ的高斯噪声。

非局部均值滤波器对（）的估计为

式中：（）为以为中心的搜索窗；（，）为由像素与周围的邻域均值计算得到的权值。

（，）按照如下定义：

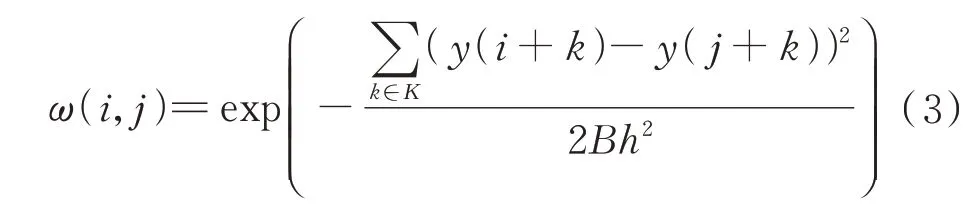
式中：为非局部滤波参数，取决于噪声水平，与噪声标准差成正比；是邻域的像素数，例如邻域大小为7×7 时，=［-3，3］×［-3，3］，=49。

1.2 SURE 在非局部均值滤波中的应用

去噪图像的均方误差（Mean Square Error，MSE）定义式为

式中：‖·‖为欧式范数；为去噪图像中的像素数。

SURE 准则提供了一种对真MSE 进行无偏估计的方法，第个像素的SURE 值表示为

据式（2）和式（3）、式（5）中偏导数表示为

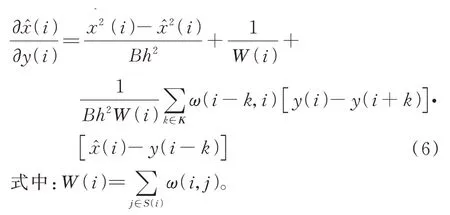
通过计算得到与每个像素的滤波参数对应的SURE 值，最小的SURE 值对应的滤波参数最佳。

2 用于INSAR 的SURE 准则非局部滤波

2.1 InSAR 相位噪声模型

InSAR 相位噪声为如下加性噪声模型：

式中：ϕ为实测 相位；ϕ为无噪声InSAR 相位；为零均值加性噪声。

由于InSAR 相位在［-π，π］的区间内存在相位跳变，无法直接应用实域中的干涉相位进行滤波，而为了正确提取目标信息，发生在缠绕相位条纹中的相位跳变应当被保留。然而，由于复数域中的InSAR 相位是连续的，且使用复数据进行干涉相位滤波的效果更佳，故采用复数域中的InSAR 相位模型：

式中：S、S分别为复数域中的实测相位和无噪声相位；n为复数域中的相位噪声。

S的实部和虚部可以分别表示为

式中：、分别为n的实部和虚部，可以将实部和虚部的噪声分别视为零均值加性噪声；是由相干性确定的相位质量指标。

2.2 提出的方法

所提出方法根据2.1 节中InSAR 相位噪声模型，在实部和虚部中分别对InSAR 相位进行SURE准则快速非局部均值滤波，从而更好地提取目标信息，流程如图1 所示。

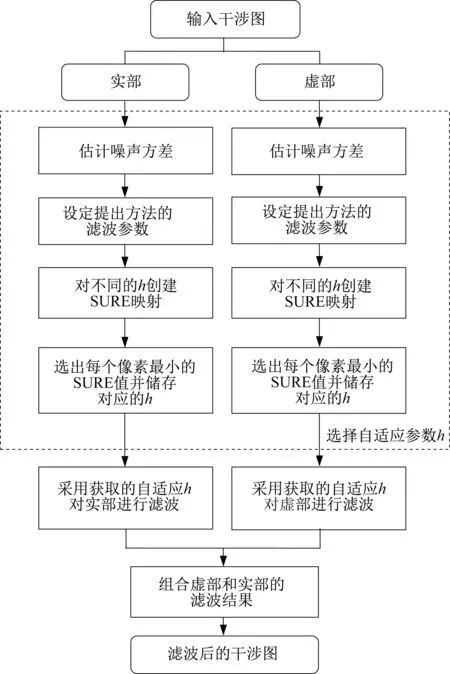
图1 InSAR 相位滤波流程Fig.1 Flow chart of InSAR phase filtering

该方法侧重于自适应的滤波参数的选择，使其适用于InSAR 实测复杂场景，尤其是城市区域的相位滤波。对于实部和虚部，选择自适应参数的步骤类似，该方法在InSAR 相位滤波中的应用步骤如下：

噪声方差估计：由于滤波参数很大程度上取决于实测数据噪声方差σ，将实部和虚部分离后，首先采用零均值加性噪声方差的估计器以获得噪声方差σ。

滤波参数设置：根据不同的数据集来设置滤波器的参数，如邻域窗的半径、搜索窗的半径以及滤波参数。不同于传统非局部均值滤波器采用固定的滤波参数，所提出方法通过比较不同数据集下不同范围的滤波结果，给出最佳滤波参数范围为=［0.55∶0.005∶0.6］×σ。

SURE 值计算：SURE 值的计算是该非局部均值滤波算法的核心。依据步骤2 中给出的滤波参数范围执行快速非局部均值滤波，同时计算每个像素的SURE 值。对于给定范围中的每个滤波参数都可以获得一个大小与原数据相同SURE值数组。

最佳滤波参数选择：在完成对给定滤波参数范围内所有的非局部均值滤波之后，为输入数据中的每个像素选择最小SURE 值，并储存对应的最佳滤波参数。比起传统非局部均值滤波器对所有像素统一选择固定的滤波参数，所提出的方法依据SURE 准则对每个像素选择相应的最佳滤波参数，对复杂场景中的不同区域具有更好的适应能力。

采用步骤2 中的滤波器窗口半径和以及获取的自适应滤波参数数组，对该部分（实部或虚部）进行快速非局部均值滤波。最后，将实部和虚部的滤波结果组合，获得滤波后的干涉相位，至此完成干涉相位滤波的所有步骤。

3 实验及结果分析

采用仿真数据和实测数据对提出方法进行实验验证，与经典Goldstein 滤波器和非自适应的原始非局部滤波器的结果进行对比分析。其中，Goldstein 滤波器的窗口大小均设置为13×13，滤波参数设置为0.5。非局部均值滤波器和所提出方法的邻域窗均设置为10×10，搜索窗大小设置为23×23。所有实验均在配置为2.60 GHz Intel Core CPU和16 GB 内存的PC 上进行。

3.1 仿真数据

仿真数据为Matlab 函数随机生成的常用仿真干涉条纹，并加入信噪比为1.406 dB 的高斯白噪声，如图2（a）所示。采用经典Goldstein，原始非局部滤波和所提出的滤波方法进行噪声抑制后的干涉条纹图如图2（b）～图2（d）所示。

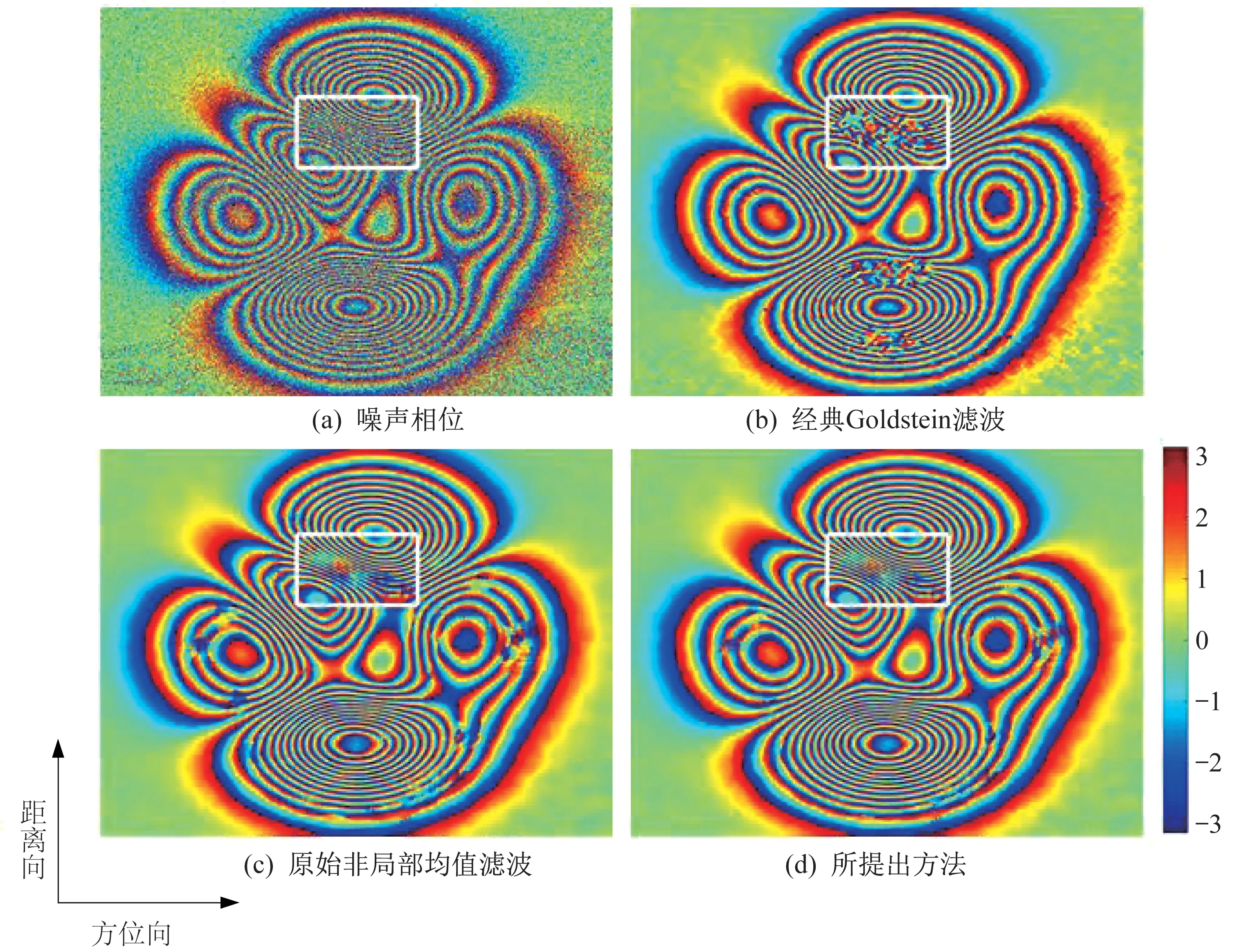
图2 仿真数据的滤波结果Fig.2 Filtering results of the simulation data

由上述可知，原始非局部均值和所提出方法的滤波结果比经典Goldstein 滤波结果更平滑。在白框标出的条纹密集区域，与图2（b）与图2（c）相比，图2（d）中条纹连续性的保持效果最佳，显示出所提出方法在条纹图案细节保持方面更优秀的性能。

此外，通过残差数（Number of Residues，NOR）和峰值信噪比（Peak Signal to Noise Ratio，PSNR）对滤波结果进行比较评估，同时给出每种方法的运行时间。仿真数据滤波结果的定量指标和运行时间见表1，较小的NOR 和较高的PSNR 表明滤波器的降噪效果更好。在3 种滤波结果中，所提出的方法获得了最大的PSNR。经典Goldstein滤波减少了98.87%的含噪干涉图的NOR，非局部均值滤波器减少了98.28%，提出的方法减少了98.50%，所有方法在噪声抑制方面的效果差别不大。

表1 仿真数据滤波评估指标对比Tab.1 Comparison of the estimated indexes for simulation data filtering

3.2 实测数据

采用TanDEM-X 获取的拉斯维加斯及其周边区域的干涉实测数据进行实验验证。该城市场景包含各种类型的建筑，便于评估不同滤波方法在城市区域滤波的效果。含噪干涉相位如图3（a）所示，经典Goldstein 滤波器、原始非局部均值滤波器和所提出方法的滤波结果分别如图3（b）～图3（d）所示。

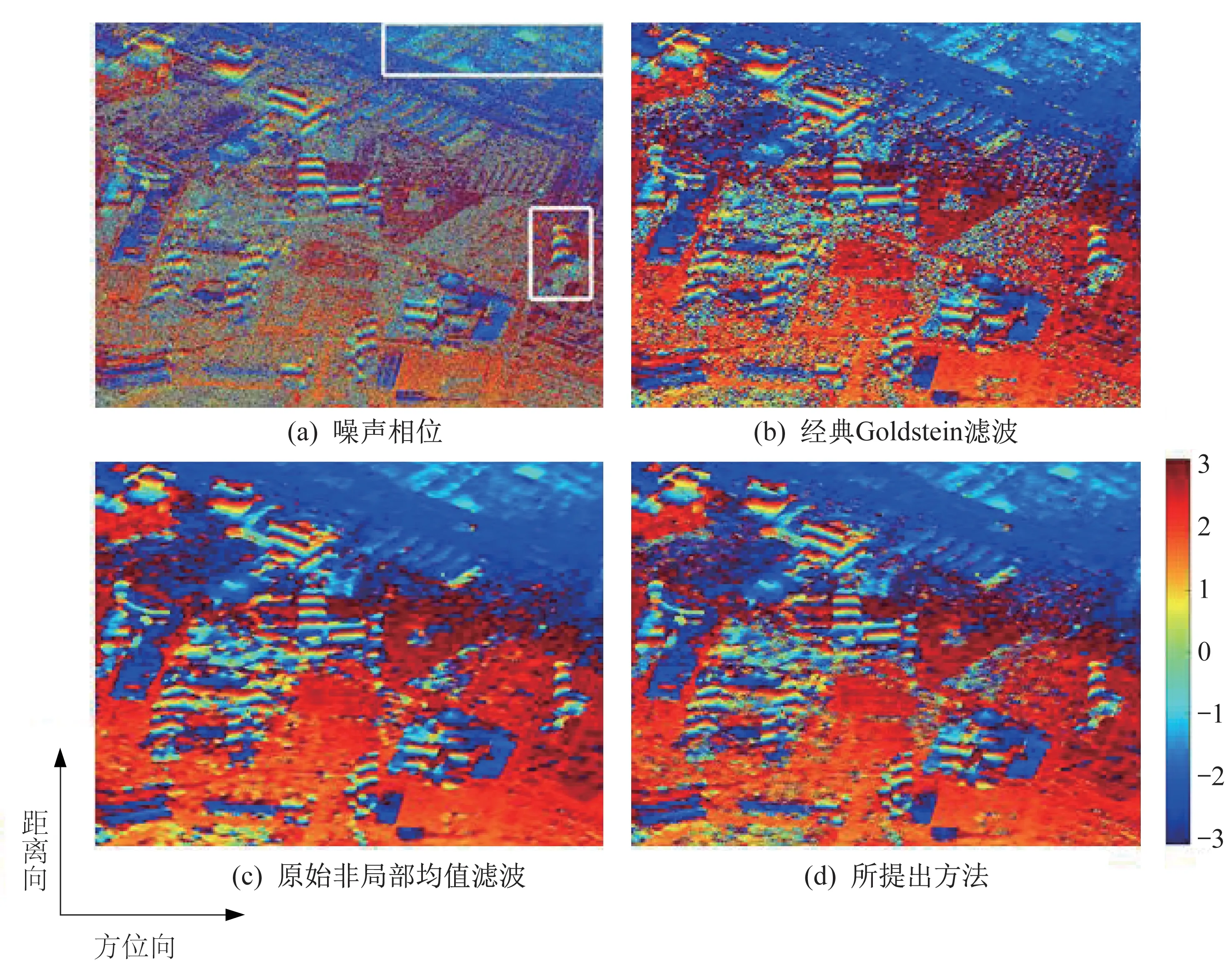
图3 实测城市数据的滤波结果Fig.3 Filtering results of the measured urban data

图3（c）中非局部均值滤波结果和图3（d）中提出方法的滤波结果可以更好地抑制相位噪声。然而，原始非局部均值滤波器的结果显示出干涉相位被过度滤波，造成更多的细节损失。此外，经典Goldstein 滤波器、原始非局部均值滤波器和所提出的方法的运行时间分别为272.406 7、4 674.544 3、3 706.487 7 s。

将图3（a）中标出的均质区域和高层建筑区域放大，以便更清楚地进行细节比较，如图4 和图5所示。

图4 实测城市数据均质区域滤波结果Fig.4 Filtering results of the homogenous areas of the measured urban data

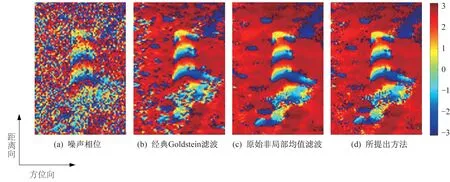
图5 实测城市高层建筑区域Fig.5 High-rise building areas of the measured urban data

对于均质区域，Goldstein 滤波器的结果明显存在更多的斑点噪声，且表2 中虽然Goldstein 滤波器获得最高的PSNR，但其只能降低62.34%的NOR。在图4（c）和图4（d）中，原始非局部均值滤波器和所提出的方法在均质区域中均呈现出较好的噪声抑制效果。原始非局部均值滤波器减少了99.88%的NOR，而提出的方法减少了97.80%的NOR，且取得了更高的PSNR。这2 种方法在均质区域的噪声抑制方面具有相似的性能。

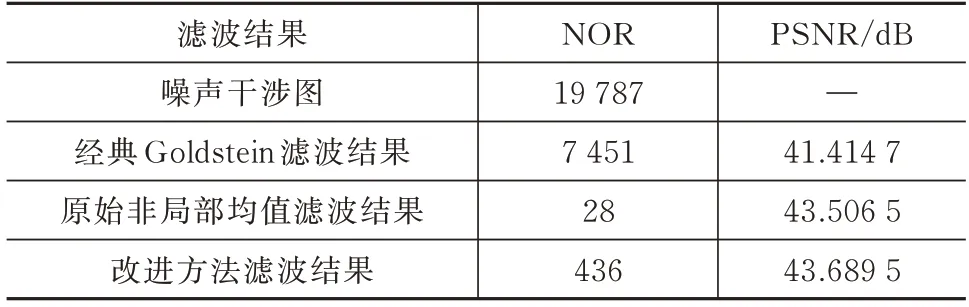
表2 均质区域滤波评估指标对比Tab.2 Comparison of the estimated indexes for the homogeneous areas

由于高层建筑的干涉条纹、边缘在城市建筑重建和高度信息的提取中起关键作用，在相位滤波中应着重保留这些基本细节。所提出方法的另一个优点在于能够更好地保持建筑区域的边缘信息。如图5 所示，与经典Goldstein 滤波器和非局部均值滤波器相比，提出方法在图5（d）中更好地保留了建筑边缘形状和条纹细节。

边缘保持度（Edge Preservation Degree of Ratio of Average，EPD-ROA）可用于验证干涉图中建筑边缘保持效果。指标更接近1 时，相应的方法在边缘保持方面的效果更好。3 种滤波方法在建筑区域的边缘保持度见表3，所提出方法的EPD-ROA比2 种传统方法更接近于1，表明该方法在水平和垂直方向上均取得了最好的边缘保持效果。

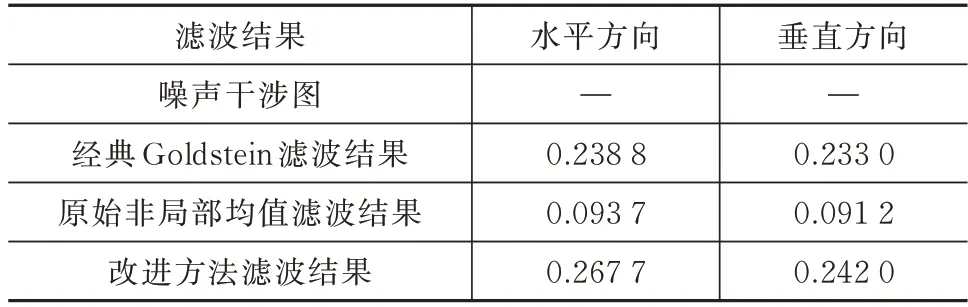
表3 建筑区域EPD-ROA 对比Tab.3 Comparison of the EPD-ROAs in the building areas

为进一步评价改进方法的整体滤波效果，采用最小二乘法对上述3 种滤波器滤波后的干涉相位解缠，以比较相位滤波结果对后续相位解缠处理的影响。解缠前的噪声干涉相位如图6（a）所示，采用3 种滤波方法进行滤波后的干涉相位解缠结果分别如图6（b）～图6（d）所示。

总体而言，Goldstein 滤波后解缠结果和所提方法滤波后的结果相似。而原始非局部均值滤波后的解缠结果对干涉图的相位保持效果较差。比较图6（b）和图6（d）中标出的建筑区域，提出的方法比Goldstein 滤波器更有效地保持建筑结构的形状，建筑边缘更为清晰。此外，所提出的方法在均质区的解缠结果比Goldstein 滤波器更平滑。

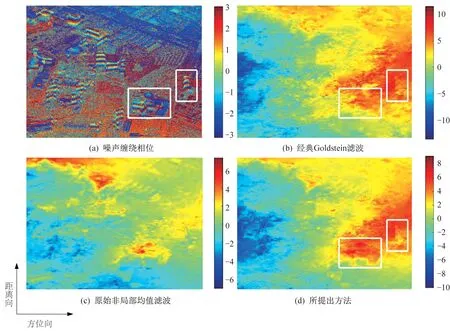
图6 实测城市数据集的解缠结果Fig.6 Results of the unwrapped phase of the measured urban data

综合考虑滤波后的缠绕相位结果和解缠相位的结果，所提出方法在均质区域与城市建筑区域均能进行有效的噪声抑制和细节保持，适用于包含多种类型建筑的复杂城市场景。

4 结束语

针对传统InSAR 相位滤波方法不能实现自适应，且在噪声抑制和细节保持能力上不能兼得的问题，介绍了一种基于SURE 准则获取自适应滤波参数的改进非局部均值滤波器，并将其应用于InSAR实测数据的干涉相位滤波。提出的方法利用InSAR 相位复数域模型，将其分为实部和虚部分别滤波，并依据SURE 准则估计最优滤波参数实现自适应，最终合并实部和虚部的结果得到滤波后的InSAR 相位。仿真数据和实测数据的实验结果均表明，该方法在时间消耗和细节保持方面优于非自适应的InSAR 非局部均值滤波器，尤其是在条纹图案的连续性和边缘信息的保留方面更优。