连续双切换线性正系统状态反馈控制
2022-07-15冉晓宇
冉晓宇,龙 飞
(1贵州大学 大数据与信息工程学院,贵阳 550025;2贵州理工学院 人工智能与电气工程学院,贵阳 550003)
0 引 言
双切换线性正系统是由一组线性子系统组成,在其子系统间切换,受控于一个有限状态的马尔可夫过程。此类系统被广泛应用于结构或参数方面存在突然随机变化的系统进行建模,模型可应用于网络控制系统、HIV突变和治疗。
在过去的几十年里,切换系统的稳定性分析一直都是一个重要的研究课题。由于电子信息工程、通信、经济学等领域中愈加复杂的控制对象,研究者越来越关注切换系统的稳定性和其控制器综合问题,切换系统的应用引起了更为广泛的关注。对于切换系统稳定性的分析,常用的分析方法有Lyapunov函数、Co-positive Lyapunov函数、驻留时间和平均驻留时间等。本研究中,选择多Lyapunov函数方法,研究双切换线性正系统,并对其有效性进行了验证。
当前的许多稳定性研究中,均假设切换系统的每个子系统都是稳定的,但在任意切换规则下的切换系统却都不能保持稳定,仅在有限的切换信号下可能是稳定的。尽管存在一些线性分析方法和工具,对于切换系统的稳定性和控制综合问题仍是一个具有挑战性的研究方向。平均驻留时间切换是一类有限的切换信号方式,切换的次数被限制在一个有限的间隔内,且平均时间不小于一个给定常数。
对于双切换线性系统,文献[3-4]基于持续驻留时间(Persistent dwell-time,PDT)的方法,研究了系统的鲁棒指数几乎处处稳定;又基于驻留时间(DT)的方法设计确定性切换,分析了系统几乎处处稳定。文献[5]用反馈切换律设计确定性切换律,分析了系统在均方稳定下的状态反馈控制器问题。文献[6]设计切换规则和使用输出反馈控制器,保证闭环系统的鲁棒渐近稳定,给出在鲁棒性能要求下可行存在的充分性判据。文献[7]针对具有平均驻留时间的切换线性控制系统,提出了一种降阶输出反馈控制方法。该方法将边界条件加入到综合控制问题中,利用多重二次Lyapunov函数,在统一的框架下,建立了具有保证稳定性的降阶输出反馈控制器,并将综合条件表述为一组具有给定的驻留时间参数的LMIs,为具有ADT切换的离散时间线性控制系统的综合提供了一种有效的、系统的方法。
本文将多Lyapunov函数、线性矩阵不等式方法与反馈控制器设计方法相结合,在平均驻留时间的方法下,得到控制器和子系统的切换规则,以保证切换系统在状态反馈控制器下的指数几乎处处稳定。
1 问题描述
考虑下面的连续双切换线性正系统:

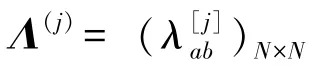
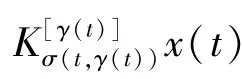
如果对于任意初始条件()≥0,对于任意的0,都有()≥0,()≥0,则系统(1)是正系统。
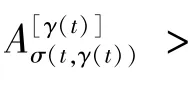
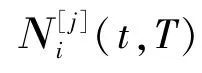
如果对称矩阵可以进行如下分块:

其中,和为对称矩阵,那么当且仅当下面条件之一成立时,为负定矩阵。条件表达式如下:
(1)0, X0
(2)0,X-S Z0
注意:以上结果完全适用于为正定矩阵的情形,只需把条件(1)、(2)中的“<”用“>”代替即可。在一些控制问题中,经常出现如下形式的不等式:

其中:,,0;0是已知相应维数的常数矩阵;为对称矩阵。
应用引理2,可将矩阵不等式的可行性问题转化为一个等价的矩阵不等式的可行性问题:
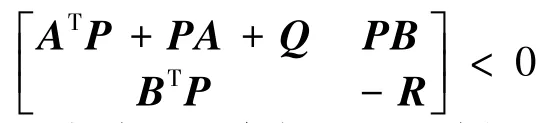
上式是一个关于矩阵变量的线性矩阵不等式。
如果所有∈R,满足:
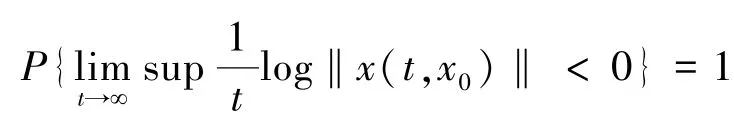
则切换系统的连续平衡点0,是指数几乎处处稳定的。
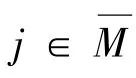
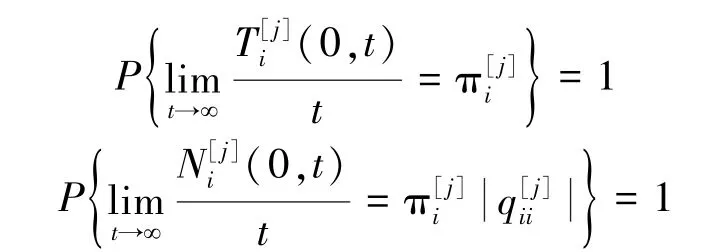

2 主要结果
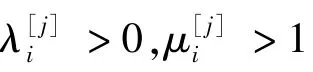
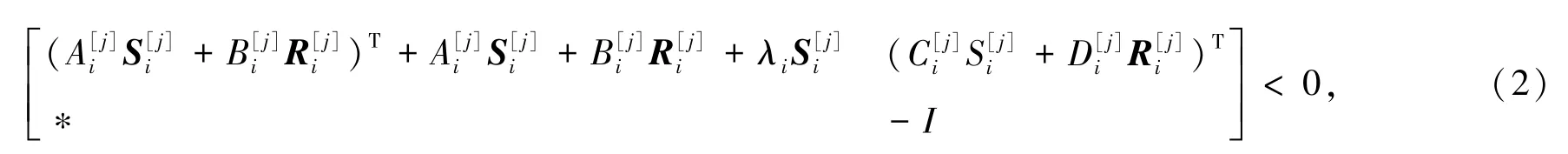

则连续双切换线性正系统(1)的切换反馈控制问题是可解的,其平均驻留时间满足:

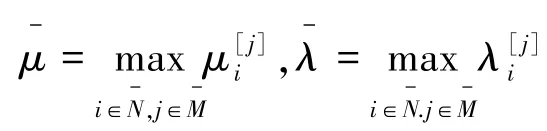
选择如下形式的多Lyapunov函数:
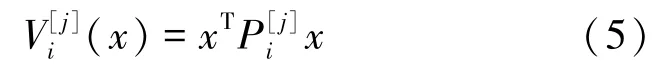

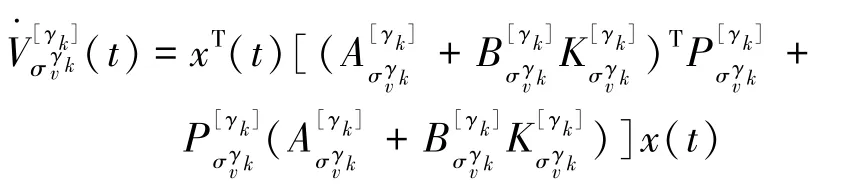
根据式(2),应用引理2,
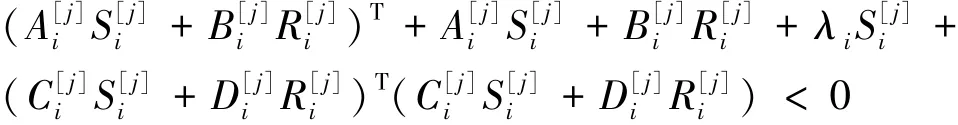

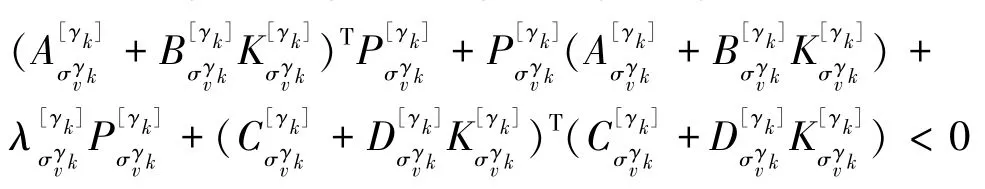
对上式左右两边分别同时左乘[()],右乘[()],可以得到:

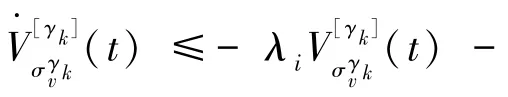
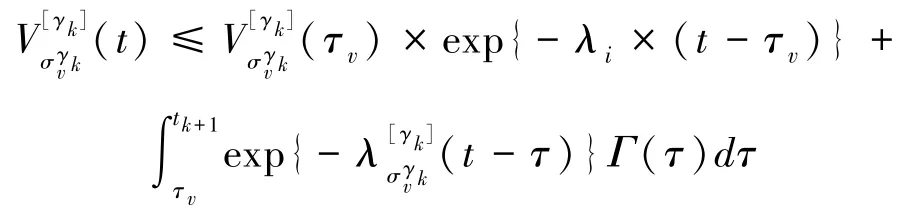
其中,()()(),假定系统干扰为0,不失一般性,令:

假设[t,t)[t,)∪[,)∪…∪[τ,t),考虑到式(3),进行相似的处理,得到:

将其代入到矩阵不等式(3)中,得到:
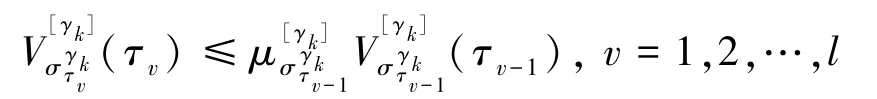
则有:

因此,对于任意∈[t,t),
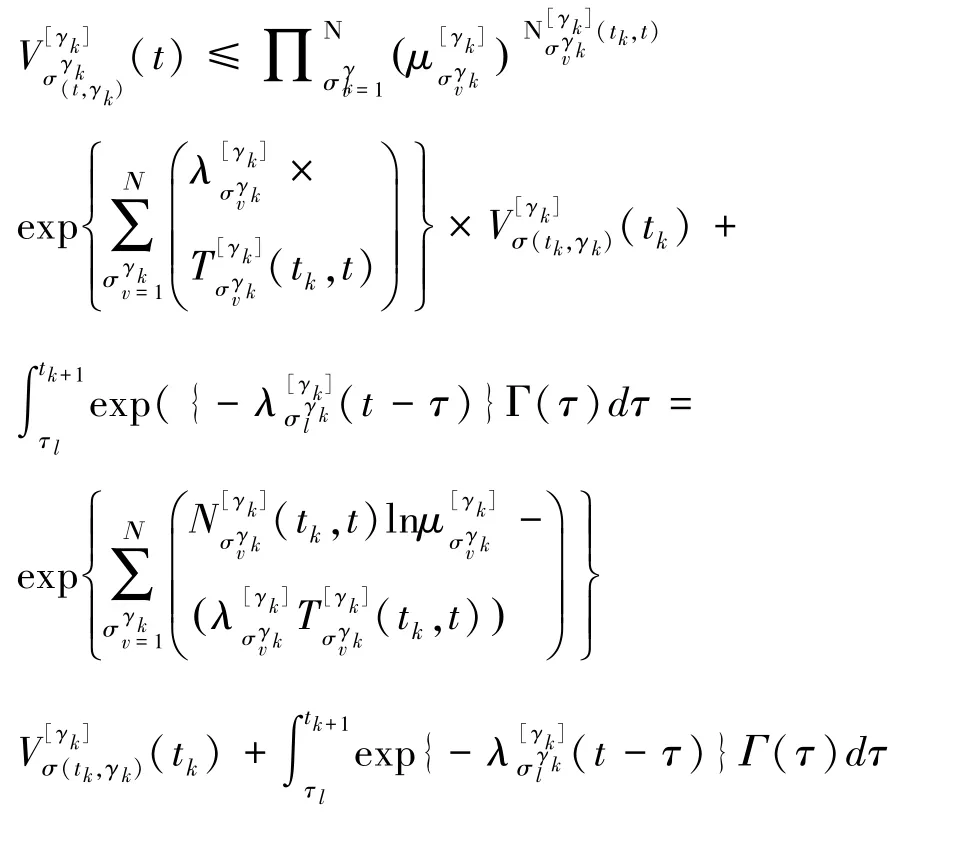
利用上式,重复此过程;对于任意0,
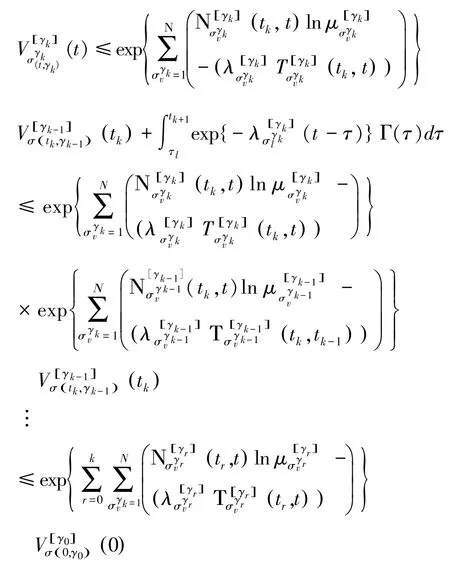
根据引理3,其中,
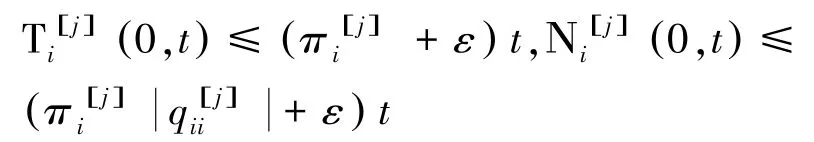
由定义2和上式不等式可知:对于任意给定的0,

对上式两边同时取二范数后再取对数,

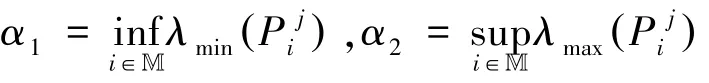

由不等式切换次数和平均驻留时间法,根据定义3,即在平均驻留时间约束的切换律下,在切换系统的平衡点x=0,是指数几乎处处稳定的,证毕。
3 数值算例
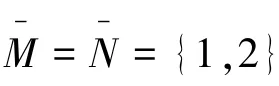
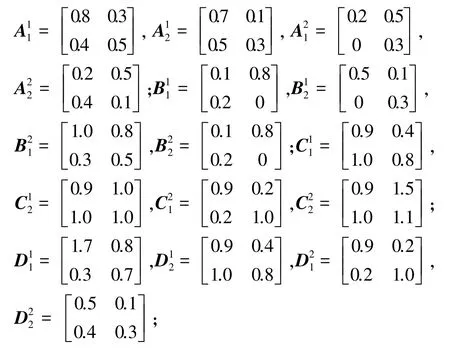
切换信号(,1)和(,2)转移概率矩阵分别为:

由公式Π[]Π[][],可以计算出平稳分布为:


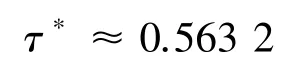
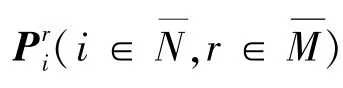
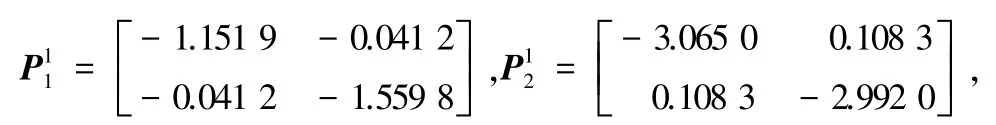

根据定理1可知,系统在所设计的切换律下及反馈控制器下是指数几乎处处稳定的,系统的切换信号图、控制信号曲线和系统状态轨迹如图1~3所示。

图1 切换信号γ(t)Fig.1 Switching signalγ(t)

图2 控制曲线u(t)Fig.2 Control curve
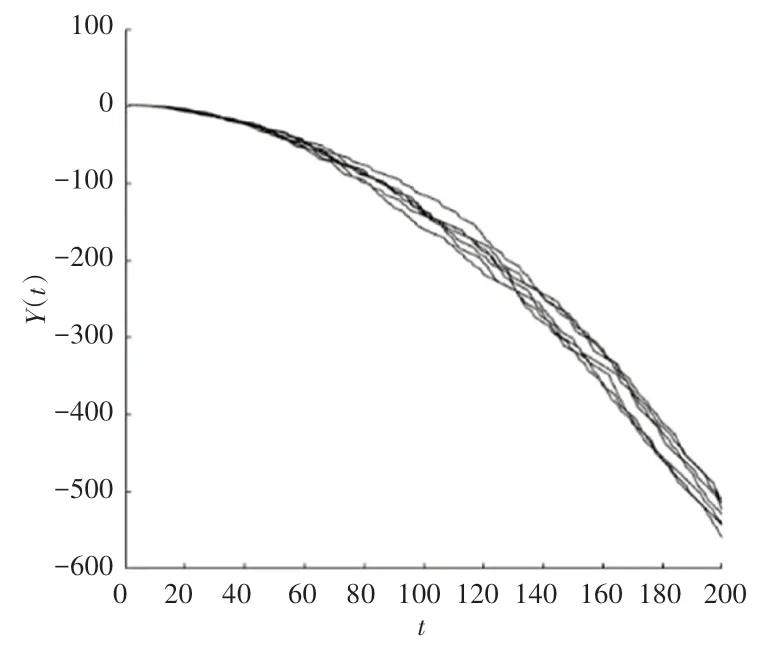
图3 ln‖x(t)‖的7次实现Fig.3 Seven realizations of ln‖x(t)‖
4 结束语
针对连续双切换线性正系统,研究了基于平均驻留时间切换的状态反馈问题,设计了系统的状态反馈控制器,构造了Lyapunov函数,根据马尔科夫过程及能量衰减原理适当的切换信号;利用线性矩阵不等式以及马尔科夫暂态分析方法,得出使得系统指数几乎处处稳定的充分条件;最后给出一个数值例子,验证了提出方法的有效性,为连续双切换线性正系统的分析提供了一种有效的方法。
