利用解题教学培养师范本科生的创新思维能力
2022-07-14仲崇轶夏顺友王常春陈治友李艳琴
仲崇轶,夏顺友*,王常春,陈治友,李艳琴
(1.贵州师范学院数学与大数据学院,贵州 贵阳 550018;2.遵义师范学院数学学院,贵州 遵义 563006;3.贵阳学院数学与信息科学学院,贵州 贵阳 550005)
0 引言
数学课堂教学不仅要传授数学知识、掌握数学方法和领会数学思想,还要强调立德树人和创新思维的培养。师范类数学专业本科生在成为一名数学教师前必须进行“上通数学,下达课堂”的数学专业知识和数学课堂教学理论以及课堂教学技能的专门培养和训练。数学课堂教学离不了“数学概念教学、数学命题教学和数学解题教学”三个基本教学内容。数学概念教学是整个教学的基础,数学命题教学是深化,数学解题教学是前两者的巩固、延伸和应用。数学解题教学在数学教学中起到举足轻重的作用,所以在解题和解题教学方面有许多好的研究成果,如波利亚的《怎样解题》和《数学解题思维策略》,罗增儒的《数学解题学引论》和《中学数学解题的理论与实践》,吴有昌和王林全等的《中学数学解题研究》等。从这些论著中可见贯彻“源于教材而高于教材,基于教材而不拘泥于教材”的解题教学才是更有效的课堂教学。因此本文将以近两年高中数学学业水平考试中的几个代表性题目为例,论述如何利用解题教学培养师范生的创新思维能力以启迪学生脱离“题海”困境,并以培养灵活的思维为导向,重在提供可以借鉴的教学题例,可以参考的教学方法,可以模仿的教学策略和教学模式。
1 平面解析几何中的点到直线的距离公式
1.1 点到直线的距离公式
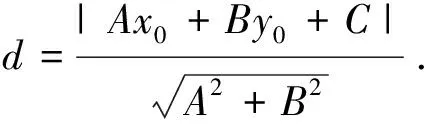
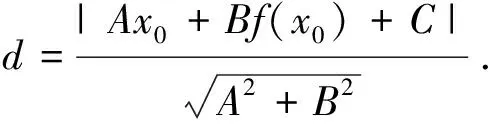
1.2 题例1(2020年12月贵州普通高中学业水平考试第35题)
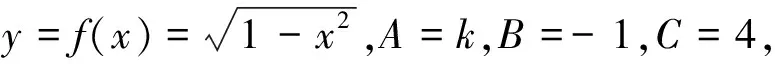
点到直线的距离公式是六个变量的一个方程,已知其中五个可求余下的一个,这是基本认识。如果考虑点P0(x0,y0)在不同的图象上,或直线l的方程有不同特征,或者把确定与不确定条件互换等,就可以创造出与题例1相似甚至更新颖的问题。
1.3 题例1培养创新思维能力的实践
学生对点到直线的距离公式的理解容易限于点的坐标和直线方程确定的情况,常重点强调直线方程必须化成一般式便于准确确定公式中的系数A、B、C,从而能准确利用公式的这个基础层面。在实际教学中,第一个层面要让学生对中学数学中所有公式,以含有未知数的等式来理解,即,把点到直线的距离公式看作一个六元方程,这有利于学生发散思维的培养,从而提升创新思维能力。第二个层面是点或直线有变动的情形,可以组织学生分组创造出相应的题目,并汇报。第三个层面是学生创新思维培养的关键教学阶段,也是课堂上学生思维最活跃的阶段。综上,通过学生讨论,引导完成下面三个问题的案例创造。
(1)点固定,直线变动的问题与解答。此处仅附一个案例(解答略去)供参考。
案例1.1:已知点P(3,1),点A(0,2),点Q是圆O:x2+y2=1上一动点,求点P到直线AQ的距离的最大值和最小值。
(2)点变化,直线固定的问题与解答。此处仅附一个案例(解答略去)供参考。
案例1.2:已知直线l的方程为x-y-6=0,点P在抛物线y=x2上,求点P到直线l的距离的最小值。
(3)点变化,直线也变化的问题与解答。此处仅附一个案例(解答略去)供参考。
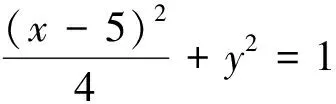
题例1中,由于圆的特殊性,问题本身虽然属于点和直线都变化的情形,但最后都归结为圆心到直线的距离来考虑,从而转为了点固定而直线变化的情形。
2 数列中裂项、叠加和迭代
在这里,仅对等差数列定义以及通项与求和之间关系中的思想方法的本质进行阐述,对不同题例的本质进行挖掘。关于等比数列的情形,可以通过类比处理。
2.1 等差数列定义以及通项与求和关系
等差数列定义的关键是递推关系。具体的, 从第二项开始,后项减前项等于公差,即
a2-a1=d
a3-a2=d
……
an-1-an-2=d
an-an-1=d
前n-1个式子叠加可得an=a1+(n-1)d.
(1)上面叠加中关键是有“相消”的特征,从而也蕴含了“裂项”的思想(式子从右往左看)。
如果改写这些式子为:
a2=a1+d
a3=a2+d
……
an-1=an-2+d
an=an-1+d.
前n-1个式子,从第一式依次往后迭代同样可以得到an=a1+(n-1)d.
(2)迭代中体现了“递推”及其反向的“递归”。 再看通项与求和的关系:
a1=S1
a2=S2-S1
a3=S3-S2
……
an-1=Sn-1-Sn-2
an=Sn-Sn-1
如果将这些式子改写为:
S1-0=a1
S2-S1=a2
S3-S2=a3
……
Sn-1-Sn-2=an-1
Sn-Sn-1=an,
此时与等差数列定义的式子的左边和右边对比,会发现它们形式上有相同之处,而不同之处在于左边字母符号不同,前者的右边是后者右边的特殊形式。
2.2 题例2(2020年12月贵州普通高中学业水平考试第43题)
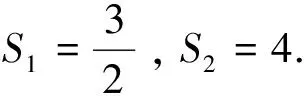
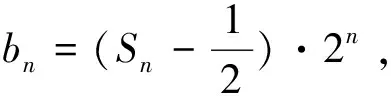
解法一:(1) 设等差数列{an}的公差为d.

从而
Tn=b1+b2+b3+…+bn-1+bn
=[12·21-(1-1)2·21-1]+[22·22-(2-1)2·22-1]+[32·23-(3-1)2·23-1]+…+[(n-1)2·2n-1-((n-1)-1)2·2(n-1)-1]+[n2·2n-(n-1)2·2n-1]
=n2·2n.
所以数列{bn}的前n项和Tn=n2·2n.
数列求和除利用等差数列与等比数列求和公式外,可以分组求和、错位相减求和、逆序相加求和、裂项求和等等。而错位相减求和,逆序相加求和、裂项求和都可以在基本题型和思想方法上进行拓展创新,以此培养学生的创新思维能力。
2.3 题例2培养创新思维能力的实践
题例2的关键是将数列{bn}的通项公式巧妙裂项为bn=n2·2n-(n-1)2·2n-1,从而叠加,相消,即b1=12·21-(1-1)2·21-1
b2=22·22-(2-1)2·22-1
…
bn-1=(n-1)2·2n-1-((n-1)-1)2·2(n-1)-1
bn=n2·2n-(n-1)2·2n-1,
这n个式子叠加,可得Tn=n2·2n.
如果对数列{bn}的通项公式裂项为
bn=(n+1)2·2n-1-2n,
则题例2的第二问有以下第二种解法。
解法二:因为
=(n+1)2·2n-1-2n,
所以,有
①
于是,有
②
①-②得
③
进而有
④
③-④得
=n2·2n.
解法一裂项最佳,叠加相消就求出了Tn,而解法二裂项后与解法一的形式有不同,所以需要利用错位相减的思想方法进行。
通过完成以下教学任务,培养学生的创新思维能力。
(1)由于解法一没有学生想到,只有部分学生想到与解法二类似的求解,因此在教学中,在学生讨论探索之后,要讲授和启发学生深刻理解等差数列定义式、通项与求和公式关系和题例2的裂项式之间的共同本质。简述如下:
等差数列定义式an+1-an=d,n=1,2,…,式中后项减前项均为常数d,而和式与通项的关系式S1=a1,Sn+1-Sn=an+1,n=1,2,…中,后项减前项都为常数d,后者是求和数列{Sn}从第二项开始的后项减前项为变数an+1,如果an+1=d,n=1,2,…,则定义式和关系式相同。因此不把Sn看作数列{an}的前n项和,比如写作an+1-an=bn+1,n=1,2,…,就容易把定义式视为关系式的一种特例。下面的案例供参考(解答略)。
案例2.1:已知数列{an},{bn}满足an+1-an=bn+1,n=1,2,…,且a1=0,以及bn=2n-1,n=1,2,…,求数列{an}的通项公式。
案例2.2:已知数列{an},{bn}满足a1=1,且an+1-an=bn+1,bn=2n,n=1,2,…,求数列{an}的通项公式。
(2)引导学生参考案例2.1和案例2.2认识题例2并构造类似新题和归类,培养创新思维能力。其实题例2第一种裂项,相对于把数列{bn}的通项理解为通项公式为an=(n-1)·2n-1,n=1,2,…的数列{an}的后项减前项,即bn=an+1-an,n=1,2,…. 而第二种裂项bn=(n+1)2·2n-1-2n的右边可以看作两个数列的通项相减,即bn=cn-dn,cn=(n+1)2·2n-1,dn=2n,此时比案例2.1和案例2.2更一般了。
(3)要求学习高阶等差数列、线性递归数列和数列差分等内容,仿题例3构造新题并写学习探索报告。
3 均值不等式
3.1 基本均值不等式
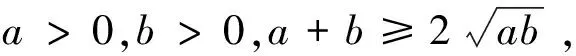
该不等式应用时除大家熟知的“一正,二定,三相等”及其推广形式外,更重要的是其中的a、b可以是较复杂的代数式。
3.2 题例3(2020年7月贵州普通高中学业水平考试第43题)
题例3:已知数列{an}的通项an=pn+q,其中p,q为常数,n∈N*.

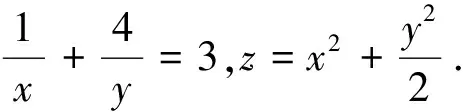
因an>0,n∈N*,故x=a2>0,y=a4>0.
于是, 有
≥2x+2y-3(当且仅当x=1,y=2时等号成立)
因为x>0,y>0,所以
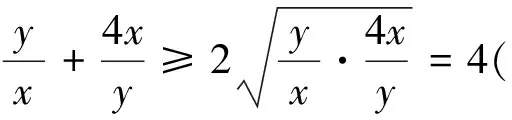
又由于x=1,y=2满足y=2x,所以,有
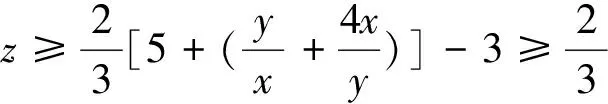
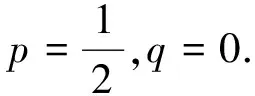
题例3比题例1和题例2难,因为要两次利用均值不等式,能做出的学生很少,亦没有同学尝试使用拉格朗日乘数法解决条件极值问题。
3.3 题例4(2019年12月贵州普通高中学业水平考试第43题)


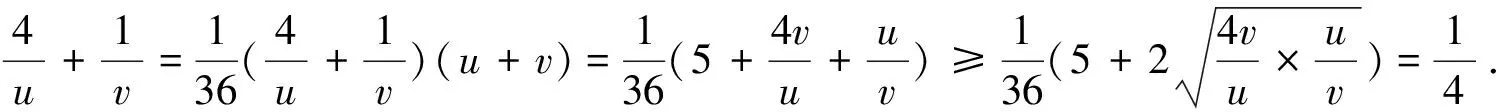
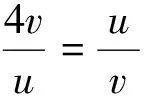
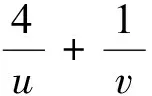
3.4 题例3与题例4解题教学中培养创新思维能力的实践
题例3与题例4之间有一定的对偶性。在解题教学中,主要利用此两题例培养学生“一题多解”和“一题多变”到解法归类和题型归类的创新思维能力。
教学实践中,通过重点完成以下教学任务,来培养学生的创新思维能力。
(1) 多种解法探索创新。题例4的其他解法参考文献[1]。在此,具体补充题例3的下列解法(简述)。
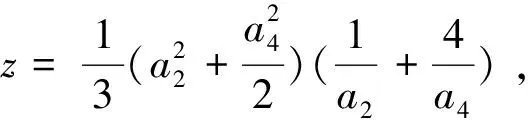
(2) 一题多变,并统一题型。具体从项数、次数和系数变化上探索“一题多变”。基于相同项数的项的次幂的倒数的线性组合和它们次幂的线性组合之一为常数,求另一个的最小值问题来统一题例3和题例4。
4 柯西不等式
4.1 基本柯西不等式
有(ac+bd)2≤(a2+b2)(c2+d2),其中a,b,c,d∈R, 当且仅当ad=bc时,等号成立。
该不等式是向量数量积的一个直接结论。应用于最大值计算时,常用于具有某两个变量的平方和为常数且另外两个变量平方和具有最大值的情形。
4.2 题例5(2019年7月贵州普通高中学业水平考试第43题)
题例5:已知数列{an}的前n项和Sn=pn2+qn,其中p,q为常数。
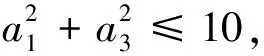
该题例利用柯西不等式处理第二问的解法见文献[2]中的法五至法九。
4.3 题例5培养创新思维能力的实践
题例5与题例3和题例4都归结为带约束的二元目标函数优化问题,但在教学实践中侧重点各有不同。通过这三个题例的问题类型异同与解法异同的比较,来培养学生的创新思维能力。
(1)多种解法探索创新。 题例5的多种解法见参考文献[3]。教学实践中,要求学生进行小组讨论,教师在旁实时引导启发。
(2)题型归类与拓展创新,并给出一般解法。
学生自主探索完成题例5归类与拓展实质为以下三类二元、二次约束条件下求二元线性目标函数z=ax+by(其中a,b为常数)的最大值问题:
①x2+y2≤M(或x2+y2=M),M为正常数;②kx2+ly2≤M(或kx2+ly2=M),其中k,l,M为正常数;③λ(kx+ly)2+μ(px+qy)2≤M(或λ(kx+ly)2+μ(px+qy)2=M),其中λ,μ,M为正常数。
(3)引导学生探索构造三类最值新题。 在此仅给出构造的三个题例(不给求解过程)供参考。
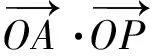
案例4.2:已知单价分别为4、7的两种商品A、B的采购量分别记为x、y,如果商品A、B采购量之间满足关系x2+2y2=6时都可以全部销售完,问商品A、B采购量分别为多少时,获得的收益最大?
案例4.3:在条件13x2+2xy+y2≤7约束下,计算目标函数z=21x+7y的最大值。
案例4.1至案例4.3以及题例5还可以考虑目标函数最小值计算方法探索。
5 总结
解题教学一般包括四个教学环节:在审题环节中弄清题目的条件与结论以及相关的知识范围等;在探索解题方法环节中寻找解题的具体方法;在陈述解题过程环节中以严密的语言表述解答的过程;在反思环节中透析题目所涉及的数学知识、数学思想和数学方法,是思维创新培训的重要阶段。 本文的教学方法、模式总结为以下三点。
第一是以自主探索、合作交流为主,结合实时点拨为辅,培养个体探索与集体合作探索相结合的培养创新思维的策略方法和教学模式。
审题阶段以学生自主完成题目的显含、隐含条件和结论以及相关知识点审定,明确是充分还是必要条件等。探索解法环节和陈述解答过程环节以小组讨论探索然后集中汇报为主。 反思环节以个体查阅资料自主探索为主,可以个体自主结对,并以一题多解和一题多变为主要形式,再集中汇报。这种体现个体与集体学习和探索的创新思维培养的策略方法和教学模式可作为培养创新思维能力的基础。
第二是在解题教学的每个环节以“变”为核心,在知识范围、条件与结论、解题方法、确定与不确定、代数与几何等等方面求变的培养创新思维的策略方法和相应教学模式。
创新思维培养的关键是不能使学生思维僵化,形成定式,因此以“变”体现特殊与一般、确定与不确定、归纳与演绎和代数与几何等求“变”求转化的动态思维策略方法与相应教学模式是解题教学培养创新思维能力的关键。
第三是以点带面,完善知识的结构化、系统化,促进思想方法的深刻化、灵活化的“归类”创新思维培养的策略方法和相应教学模式。
数学知识、思想方法及其应用不是独立单一的,是相互联系且具有一定结构的系统化体系。通过解题教学完善并强化知识结构化和系统化以及思想方法理解的深刻化等“归类”创新思维培养的策略方法和相应教学模式是解题教学培养创新思维能力的重要目标。
其它解题教学的理论、策略和方法等可参考文献[1-6]。
