高二数学测试
2022-07-14
一、单项选择题(本大题共8小题,每小题5分,计40分)
1.已知a=(1,2,3),b=(1,0,1),c=a-2b,d=ma-b,若c⊥d,则m等于( )
(A)0 (B)1 (C)2 (D)-1
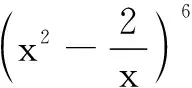
(A)240 (B)-240
(C)480 (D)-480
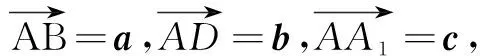

4.在7道题中有5道数学题和2道物理题,如果不放回地依次抽取两道题,则在第一次抽到数学题的前提下,第二次也抽到数学题的概率是( )
5.某电视台一节目收视率很高,现要连续插播4个广告,其中2个不同的商业广告和2个不同的公益宣传广告,要求最后播放的必须是商业广告,且2个商业广告不能连续播放,则不同的播放方式有( )
(A)8种 (B)16种 (C)18种 (D)24种
6.某种种子每粒发芽的概率都为0.9,现播种了1 000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X的数学期望为( )
(A)100 (B)200 (C)300 (D)400
7.二项式(1+x)2+(1+x)3+…+(1+x)20的展开式中,含x2项的系数为( )
(A)1 140 (B)1 330
(C)190 (D)210
8.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中华文化,阴阳术数之源,其中河图排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中.如图,白圈为阳数,黑点为阴数.若从这10个数中任取3个数,则这3个数中至少有2个阳数的概率为( )

二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求 全部选对的得5分,部分选对的得2分,有选错的得0分)
9.在二项式(1-4x)8的展开式中,下列结论正确的是( )
(A)第5项的系数最大
(B)所有项的系数和为38
(C)所有奇数项的二项式系数和为-27
(D)所有偶数项的二项式系数和为27
10.某工程队有卡车、挖掘机、吊车、混凝土搅拌车4辆工程车,将它们全部派往3个工地进行作业,每个工地至少派一辆工程车,共有多少种方式?下列结论正确的有( )
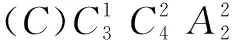
11.已知空间中三点A(0,1,0),B(2,2,0),C(-1,3,1),则下列说法正确的是( )
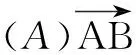
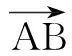
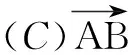
(D)平面ABC的一个法向量是(1,-2, 5)

(A)若n=1,则H(X)=0
(B)若n=2,则H(X)随着p1的增大而增大

(D)若n=2m,随机变量Y所有可能的取值为1,2,…,m,且P(Y=j)=pj+p2m+1-j(j=1,2,…,m),则H(X)≤H(Y)
三、填空题(本大题共4小题,每小题5分,计20分)
13.已知向量a=(1,-2,1),a+b=(-1,2,-1),则向量b=______.
14.在(1+x)n(n∈N*)的二项展开式中,若只有x5的系数最大,则n=______.
15.甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4∶1获胜的概率是______.
16.已知(2x-1)100=a0+a1x+a2x2+…+a100x100,记n=a1+2a2+3a3+…+100a100,则n=______.
四、解答题(本大题共6小题,计70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)为了庆祝建党一百周年,某班准备举行一场小型晚会,晚会有三个歌唱节目和两个舞蹈节目,要求排出一个节目单.(用数字作答)
(1)两个舞蹈节目要排在一起,有多少种排法?
(2)前3个节目中要有舞蹈节目,有多少种排法?



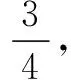
(1)假设这名队员投篮5次,求恰有2次投中的概率;
(2)假设这名队员投篮3次,每次投篮,投中得1分,未投中得0分;在3次投篮中,若有2次连续投中,而另外一次未投中,则额外加1分;若3次全投中,则额外加3分.记ξ为队员投篮3次后的总的分数,求ξ的分布列及期望.
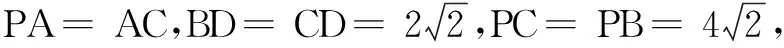
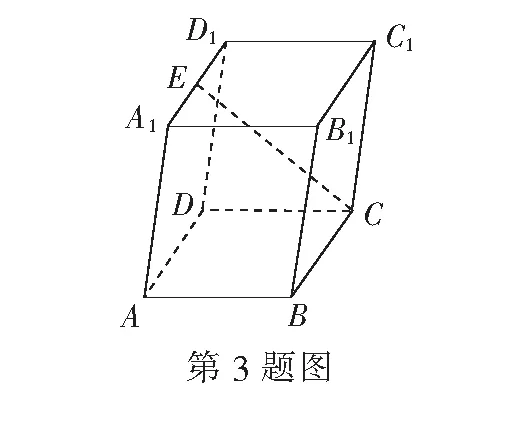
(1)求证:DE∥平面PAC
(2)线段BC上是否存在一点T,使得二面角T-DA-B为直二面角?若存在,试指出点T的位置;若不存在,请说明理由.

21.(本小题满分12分)某公司计划购买2台机器,该种机器使用三年后即被淘汰,机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
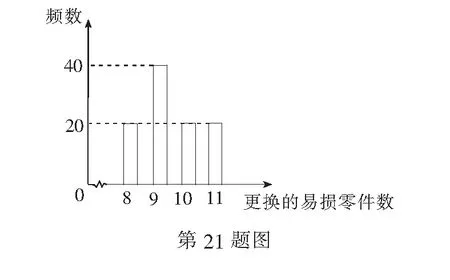
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记X表示2台机器三年内共需更换的易损零件数,n表示购买2台机器的同时购买的易损零件数.
(1)求X的分布列;
(2)若要求P(X≤n)≥0.5,确定n的最小值;
(3)以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?
22.(本小题满分12分)已知f(x,y)=(ax+by+1)n(常数a,b∈Z,n∈N*且n≥2).


(2)若f(x,y)展开式中不含x的项的系数的绝对值之和为729,不含y的项的系数的绝对值之和为64,求n的所有可能值.
参考答案
一、单项选择题
1.A;2.A;3.A;4.D;5.A;
6.B;7.B;8.C
二、多项选择题
9.BD;10CD;11.BD12.AC.
三、填空题
13.(-2,4,-2);14.10;
15.0.18;16.200.
四、解答题




(2)由题意,ξ的所有可能取值为0,1,2,3,6.
故ξ的分布列为

ξ01236 p1649649649322764

又点E为BC的中点,所以DE⊥BC.
因为平面BDC⊥平面ABC,平面BDC∩平面ABC=BC,所以DE⊥平面ABC.

又AC∩AB=A,所以PA⊥平面ABC.
所以DE∥PA.结合PA⊂平面PAC,DE⊄平面PAC,得DE∥平面PAC.
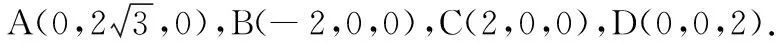
设存在点T(λ,0,0),使T-DA-B为直二面角,易知-2≤λ≤2,且λ≠0.
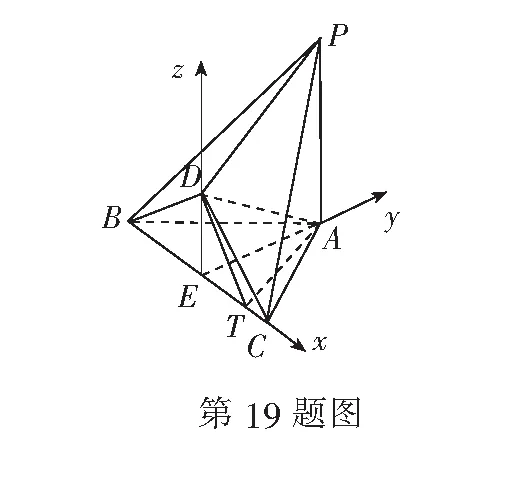

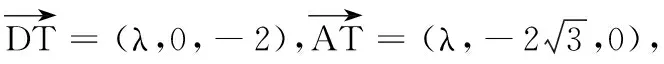

所以当点T为线段BC上靠近点C的八等分点时,二面角T-DA-B为直二面角.
21.(1)由柱状图并以频率代替概率,可得一台机器在三年内需更换的易损零件数为8,9,10,11的概率分别为0.2,0.4,0.2,0.2.
P(X=16)=0.2×0.2=0.04,P(X=17)=2×0.2×0.4=0.16,P(X=18)=2×0.2×0.2+0.4×0.4=0.24,P(X=19)=2×0.2×0.2+2×0.4×0.2=0.24,P(X=20)=2×0.2×0.4+0.2×0.2,P(X=21)=2×0.2×0.2=0.08,P(X=22)=0.2×0.2=0.04.
所以X的分布列为

X16171819202122P0.040.160.240.240.20.080.04
(2)由(1)中分布列知P(X≤18)=0.44,P(X≤19)=0.69,故n的最小值为19.
(3)购买零件所用费用含两部分,其中一部分
为购买零件的费用,另一部分为备件不足时额外购买的费用.当n=19时,费用的期望为19×200+500×0.2+1000×0.08+1500×0.04=4040;当n=20时,费用的期望为20×200+500×0.08+1000×0.04=4080.
可知当n=19时所需费用的期望值小于n=20时所需费用的期望值,故应选n=19.
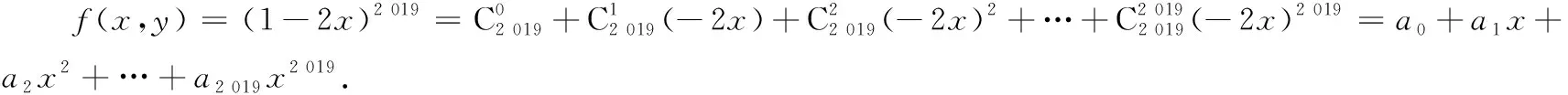
① 令x=0,得a0=1;令x=1,得a0+a1+a2+…+a2 019=(-1)2 019=-1.
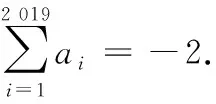
② 在(1-2x)2 019=a0+a1x+a2x2+…+a2 019x2 019中,两边同时对x求导,可得-4 038(1-2x)2 018=a1+2a2x+…+2 019a2 019x2 018.
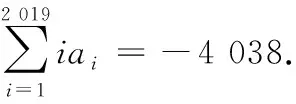
(2)令a=0,得f1(x,y)=(by+1)n,依题意,得(|b|+1)n=729.
令b=0,得f2(x,y)=(ax+1)n,依题意得(|a|+1)n=64.
因为64所有底数与指数均为正整数的指数式拆分为:82,43,26,所以当n=2时,|a|=7,|b|=26;当n=3时,|a|=3,|b|=8;当n=6时,|a|=1,|b|=2.
故n的所有的可能值为2,3,6.
