火箭发射前后3.5 h内高空风差异特征及预报

程胡华 成 巍 沈洪标 赵 亮

1)(中国人民解放军63729部队， 太原 030027) 2)(北京应用气象研究所， 北京 100029) 3)(中国人民解放军32018部队， 北京 100094) 4)(中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室， 北京 100029)

引 言

运载火箭发射前，除需确保运载火箭本身无任何问题外，还需充分考虑高空风对运载火箭安全飞行的影响，若高空风过大，轻则影响火箭发射精度，重则导致箭体弯曲折断，造成飞行失败。为提高运载火箭飞行成功率开展的研究主要分为两方面:一方面是针对运载火箭的飞行控制、发动机特性等的研究[1-5]，另一方面是针对大气环境产生的气动载荷特征的研究[6-12]，这些研究取得大量有意义成果，为持续提高火箭飞行成功率提供有力支撑。

目前，火箭飞行前较少考虑高空风可能出现急剧变化，然而实践表明：虽然高空风在短时间内变化通常较小，但有时也会出现急剧变化，如当强对流天气系统在火箭发射场及其周边发生发展时，强烈的垂直运动引起大气环境场(风场、温度场等)快速变化[13-16]，导致高空风在几小时内出现明显变化。另外，高空急流也会引起高空风急剧变化。高空急流集中在对流层上部或平流层，具有强水平切变和垂直切变，有1个或多个风速极大值(风速超过 30 m·s-1)，高空急流具有南北摆动、下沉或上升等运动特征，对其他天气系统存在动力作用[17-20]，导致高空风在短时内出现急剧变化。

因此，鉴于高空风在短时内可能出现明显时空变化，若以发射前3 h高空风产生的最大气动载荷是否超过阈值判断火箭能否按计划发射，存在一定决策风险；但发射前3 h高空风能否代表发射时刻的高空风，尚未见到相关报道。由于缺少火箭发射时刻的高空风资料，仅有火箭发射后0.5 h的高空风资料，因此利用2014年12月—2020年12月时间间隔为3.5 h的高空风资料研究火箭发射前后3.5 h 内高空风差异，利用WRF(Weather Research and Forecast)模式和发射前3 h的高空风资料，建立火箭发射后0.5 h高空风预报模型，并对发射后0.5 h 高空风预报效果进行检验。

1 资料与方法

1.1 资 料

高空风资料为2014年12月—2020年12月某地区时间间隔为3.5 h的探空气球风场资料集，共有325组样本，其中0～10 km高度和10～20 km高度范围内的间隔分别为0.20 km和0.50 km。考虑到该地区海拔高度约为1.5 km，因此高空风资料的海拔高度(简称高度，下同)范围为1.5～21.5 km。

NCEP/GFS资料为美国国家环境预报中心(National Centers for Environmental Prediction，NCEP)全球预报系统(Global Forecast System，GFS)模式预报产品，该资料每日发布4次(08:00，14:00，20:00和02:00，北京时，下同)，可以预报未来8 d的天气，水平分辨率为0.5°×0.5°，1°×1°，1.5°×1.5° 等，NCEP/GFS预报产品已广泛应用于天气预报、天气机理等方面研究，并取得一系列成果[21-23]。本文选用水平分辨率为1°×1°的NCEP/GFS预报场作为WRF模式的初始场和侧边界条件，结合火箭发射前3 h 高空风资料，制作未来24 h内的短期高空风预报模型。

1.2 方 法

以火箭发射前3 h高空风为基准，对3.5 h内的高空风速偏差、绝对偏差、相对误差绝对值及风向绝对偏差进行统计，相应的计算公式如下：

(1)

(2)

(3)

(4)

式(1)～式(4)中,D为风速偏差(单位：m·s-1),A为风速绝对偏差(单位：m·s-1),R为风速相对误差绝对值(单位：%),C为风向绝对偏差(单位：(°))，n为样本量，x为发射后0.5 h高空风速(单位：m·s-1)，y为发射前3 h高空风速(单位：m·s-1)，k为发射后0.5 h高空风向(单位：(°))，l为发射前3 h高空风向(单位：(°))。占有率为某区间范围内样本量占总样本量的百分比。

WRF模式是目前世界上最先进的中尺度数值天气模式之一，能够客观描述从云尺度到各种不同天气尺度的重要天气特征。目前WRF模式已被广泛应用于天气预报业务、天气机理等研究，利用该模式可较好地预报强对流、高空急流、地面风等变化特征及演变机理,并取得大量成果[18-19,24-26]。火箭发射前3 h、发射后0.5 h的高空风分别以V1和V2表示，基于发射前3 h高空风V1和WRF模式建立高空风预报模型得到发射后0.5 h的高空风预报，以Vf表示。

2 火箭发射前后3.5 h内高空风差异

2.1 最大风速偏差

图1a是火箭发射前后3.5 h内最大风速偏差箱线图，图中上、下黑色横线分别代表风速最大值和最小值，黑色方框的上、下边分别对应上四分位数(75%)和下四分位数(25%)，方框内黑色线为中分位(50%)。由图1a可见，最大风速偏差值范围为-24.00～26.00 m·s-1，中分位数为-5.00 m·s-1，上四分位数为8.00 m·s-1，下四分位数为-8.00 m·s-1。将速度偏差分为(-∞，-20 m·s-1),[-20 m·s-1，-10 m·s-1),[-10 m·s-1，0),[0，10 m·s-1),[10 m·s-1，20 m·s-1)和[20 m·s-1，+∞)6个区间，其占有率分别为0.92%，14.15%，40.92%(最大)，27.38%，14.46%和2.17%，即位于±10 m·s-1范围内的偏差占有率为68.30%，达到总数的三分之二。图1b是最大风速偏差对应高度箱线图，图中“+”表示异常值或离群点(下同)。由图1b可知，高度范围为1.7～19.0 km，中分位数为9.3 km，上四分位数为11.5 km，下四分位数为6.45 km。将高度划分为[1.5 km，6.5 km)，[6.5 km，11.5 km)，[11.5 km，16.5 km)和[16.5 km，21.5 km]4个区间，其占有率分别为25.85%，49.54%(最大)，16.62%和7.99%。图1表明：在火箭发射前后3.5 h内最大风速偏差主要集中在[-10 m·s-1，0)，在±10 m·s-1范围内的占有率达到总数的三分之二，且主要出现在对流层中高层[6.5 km，11.5 km)高度。

图1 火箭发射前后3.5 h内最大风速偏差(a)及其对应高度(b)箱线图Fig.1 Box plot of the maximum wind speed deviation(a) and corresponding height(b) within 3.5 hours before and after rocket launch

2.2 最大风向绝对偏差

图2a是火箭发射前后3.5 h内最大风向绝对偏差箱线图。由图2a可知,风向偏差范围为10.00°～180°，中分位数为69.00°，上四分位数为125.25°，下四分位数为40.00°。将偏差划分为[0°，30°)，[30°，60°)，[60°，90°)，[90°，120°)，[120°，150°)和[150°，180°] 6个区间，其占有率分别为13.54%，28.31%(最大)，20.92%，11.08%，7.69%和18.46%。图2b是最大风向绝对偏差对应高度分布箱线图，其值范围为1.7～19.5 km，中分位数为3.3 km，上四分位数为9.1 km，下四分位数为1.9 km。将高度划分为[1.5 km，6.5 km)，[6.5 km，11.5 km)，[11.5 km，16.5 km)和[16.5 km，21.5 km] 4个区间，其占有率分别为68.92%(最大)，8.92%，0.92%和21.24%。图2表明:火箭发射前后3.5 h内最大风向绝对偏差主要集中在[30°，60°)，且主要出现在对流层中低层[1.5 km，6.5 km)高度。

图2 火箭发射前后3.5 h内最大风向绝对偏差(a)及其对应高度(b)箱线图Fig.2 Box plot of the maximum absolute wind direction deviation(a) and corresponding height(b) within 3.5 hours before and after rocket launch

2.3 不同高度的火箭发射前后3.5 h内高空风差异

在 [1.5 km，6.5 km),[6.5 km，11.5 km),[11.5 km，16.5 km)和[16.5 km，21.5 km]高度内，火箭发射前后3.5 h内的平均风速偏差、绝对偏差、相对误差绝对值和风向绝对偏差在不同区间范围内占有率分布如图3所示。由图3a可知，风速偏差占有率随风速偏差增加呈先增大后减小的变化趋势，各高度的最大占有率均位于[-2 m·s-1，0)，分别为45.23%，30.15%，37.23%和41.54%。由风速绝对偏差(图3b)可知，各高度的最大占有率分别位于区间[2 m·s-1，4 m·s-1)，[2 m·s-1，4 m·s-1)，[2 m·s-1，4 m·s-1)和[0，2 m·s-1)，分别为49.85%，46.15%，54.46%和49.85%。由风速相对误差绝对值(图3c)可知，各高度的最大占有率分别位于区间[20%，30%)，[10%，20%)，[0，10%)和[10%，20%)，分别为28.00%,40.62%,67.08%和40.62%。当风速相对误差绝对值超过20%，各高度的占有率分别为71.38%(最大)，26.15%，6.46%(最小)和35.69%，即在 [1.5 km，6.5 km)高度明显偏大(71.38%)，在[11.5 km，16.5 km)高度明显偏小(6.46%)。由风向绝对偏差(图3d)可知，各高度的最大占有率分别位于区间[10°，20°)，[0°，10°)，[0°，10°)和[0°，10°)，分别为37.54%，58.46%，88.62%和51.38%。当风向绝对偏差超过20°，各高度占有率分别为41.23%(最大)，12.62%，2.77%(最小)和20.31%，即在[1.5 km，6.5 km) 高度明显偏大(41.23%)，在[11.5 km，16.5 km)高度明显偏小(2.77%)。由上述分析可知，风速相对误差绝对值、风向绝对偏差在[1.5 km，6.5 km)高度内均明显偏大，在[11.5 km，16.5 km)高度内明显偏小。

图3 不同高度范围火箭发射前后3.5 h内风速偏差(a)、绝对偏差(b)、相对误差绝对值(c)和风向绝对偏差(d)占有率Fig.3 Occupancy of wind speed deviation(a),absolute deviation(b),absolute relative error(c) and absolutewind direction deviation(d) at different height within 3.5 hours before and after rocket launch

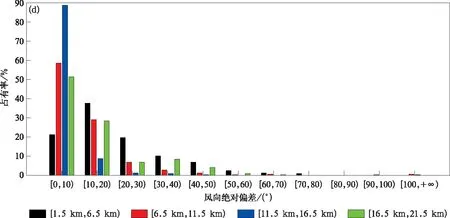
续图3

2.4 火箭发射前3 h平均风速对3.5 h内高空风差异影响

V1是决定火箭能否按计划发射的重要高空风，计算V1在整个高度范围内的平均风速得到V1平均值，将其依小到大排序以分析火箭发射前后3.5 h内风速偏差、绝对偏差、相对误差绝对值、风向绝对偏差的变化特征具有实际意义,如图4所示。由图4可知，随V1平均值增大，风速偏差振幅呈增大趋势,线性趋势呈减小特征，风速绝对偏差呈明显增大趋势，风速相对误差绝对值和风向绝对偏差均呈减小趋势，对应线性趋势方程分别为y=-0.0321x+0.3371,y=0.0628x+1.4320,y=-0.7206x+36.8890和y=-0.5878x+26.9220，即当V1平均值增大10 m·s-1，风速偏差减小0.321 m·s-1，风速绝对偏差增加0.628 m·s-1，风速相对误差绝对值减小7.206%，风向绝对偏差减小5.878°。因此，高空风强时，风向不易发生短时变化。

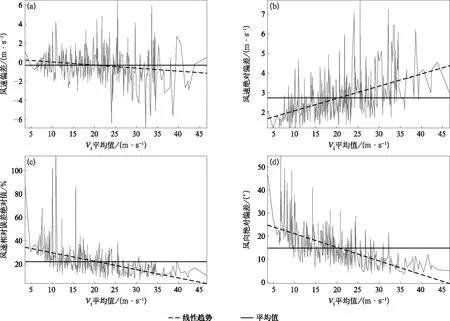
图4 火箭发射前后3.5 h内风速偏差(a)、绝对偏差(b)、相对误差绝对值(c)和风向绝对偏差(d)随V1变化特征Fig.4 Variation of wind speed deviation(a),absolute deviation(b),absolute relative error(c) and absolute wind direction deviation(d) with V1 within 3.5 hours before and after rocket launch

2.5 火箭发射前后3.5 h内高空风差异随高度变化

V1平均值从小到大排序，选取每20%样本量作为1组样本(共5组)，其中样本1为前20%的样本量，依次类推，样本5为最后的20%样本量。5组样本的风速偏差、绝对偏差、相对误差绝对值和风向绝对偏差随高度变化特征见图5。由图5可见，样本1～样本5的风速偏差(图5a)范围分别为-1.33～0.74 m·s-1，-1.27～0.56 m·s-1，-0.82～1.74 m·s-1，-0.91～0.66 m·s-1和-1.95～0.70 m·s-1，平均值分别为-0.09 m·s-1，-0.23 m·s-1，0.07 m·s-1，-0.31 m·s-1和-1.05 m·s-1；样本1～样本5的风速绝对偏差(图5b)均表现为随高度增加先增大后减小的趋势，风速绝对偏差范围分别为1.06～2.78 m·s-1,1.56～3.27 m·s-1,1.62～3.82 m·s-1,2.04～4.87 m·s-1和1.94～5.44 m·s-1，平均值分别为1.98 m·s-1，2.34 m·s-1，2.67 m·s-1，3.09 m·s-1和3.54 m·s-1，即V1平均值越大，火箭发射前后3.5 h内风速绝对偏差越大；与风速绝对偏差变化特征相反，样本1～样本5的风速相对误差绝对值(图5c)均表现为随高度增加先减小后增大的趋势，即风速相对误差绝对值在顶层和底层较大，中层较小，风速相对误差绝对值范围分别为14.89%～75.82%，7.94%～85.26%，6.21%～68.30%，5.40%～70.88%和5.20%～68.00%，平均值分别为33.16%，24.53%，20.09%，17.53%和14.60%，即V1平均值越大，火箭发射前后3.5 h内风速相对误差绝对值越小；与风速相对误差绝对值类似，样本1～样本5的风向绝对偏差也表现为随高度增加先减小后增大的趋势(图5d)，即风向绝对偏差在顶层和底层较大，中层较小，风向绝对偏差范围分别为9.34°～51.10°，5.14°～32.86°，4.02°～43.61°，3.78°～36.99°和3.25°～31.21°，平均值分别为23.60°，16.83°，13.94°，11.58°和8.31°，即V1平均值越大，火箭发射前后3.5 h内风向绝对偏差越小。由上述分析可知，V1平均值越大，火箭发射前后3.5 h内风速绝对偏差越大，风速相对误差绝对值和风向绝对偏差均越小。

图5 样本1～样本5在火箭发射前后3.5 h内的风速偏差(a)、绝对偏差(b)、相对误差绝对值(c)和风向绝对偏差(d)随高度变化特征Fig.5 Variation of wind speed deviation(a),absolute deviation(b),absolute relative error(c) and absolute wind direction deviation(d) with height for sample 1-sample 5 within 3.5 hours before and after rocket launch

2.6 不同季节火箭发射前后3.5 h内高空风差异

不同季节火箭发射前后3.5 h内风速偏差、绝对偏差、相对误差绝对值和风向绝对偏差随高度变化特征如图6所示。由图6可见，风速偏差(图6a)除冬季以负值为主外，在其他季节均表现为正值、负值交替变化，春季、夏季、秋季、冬季的风速偏差范围分别为-1.48～0.96 m·s-1，-1.11～1.24 m·s-1，-1.08～0.52 m·s-1和-1.26～0.36 m·s-1，平均值分别为-0.25 m·s-1，-0.04 m·s-1，-0.15 m·s-1和-0.74 m·s-1，即各季节平均风速偏差均为负值，且冬季明显偏大、夏季明显偏小；春季、夏季、秋季、冬季的风速绝对偏差(图6b)均表现为随高度增加先增大后减小的趋势，风速绝对偏差范围分别为1.75～4.22 m·s-1，1.05～3.58 m·s-1，1.73～3.30 m·s-1和1.68～5.11 m·s-1，平均值分别为3.00 m·s-1，2.33 m·s-1，2.43 m·s-1和3.10 m·s-1，由小到大依次为夏季、秋季、春季、冬季；与风速绝对偏差变化特征相反，春季、夏季、秋季、冬季的风速相对误差绝对值(图6c)均表现为随高度增加先减小后增大趋势，即风速相对误差绝对值在顶层和底层较大，中层较小，风速相对误差绝对值范围分别为6.89%～57.98%，11.34%～93.39%，6.59%～76.33%和5.61%～62.92%，平均值分别为24.67%，23.81%，21.01%和15.62%，由小到大依次为冬季、秋季、夏季、春季；类似风速相对误差绝对值的变化特征，春季、夏季、秋季、冬季的风向绝对偏差(图6d)也表现为随高度增加先减小后增大趋势，即风向绝对偏差在顶层和底层较大，中层较小，风向绝对偏差范围分别为5.20°～37.78°，9.13°～48.38°，4.87°～39.64°和3.26°～34.52°，平均值分别为16.33°，19.33°，15.33°和10.20°，由小到大依次为冬季、秋季、春季、夏季。由上述分析可见，冬季火箭发射前后3.5 h内风速绝对偏差较大，风速相对误差绝对值和风向绝对偏差较小，夏季火箭发射前后3.5 h 内风速绝对偏差较小、风速相对误差绝对值和风向绝对偏差较大，鉴于冬季高空风较大、夏季高空风较小，火箭发射前后3.5 h内高空风差异随季节的变化与高空风季节特征有关，该结论与图5基本吻合。

图6 不同季节火箭发射前后3.5 h内风速偏差(a)、绝对偏差(b)、相对误差绝对值(c)和风向绝对偏差(d)随高度变化特征Fig.6 Variation of wind speed deviation(a),absolute deviation(b),absolute relative error(c) and absolute wind direction deviation(d) with height within 3.5 hours before and after rocket launch in different seasons

3 建模分析

3.1 个例选取

从2014年12月—2020年12月共325组高空风样本中选取整个高度范围内火箭发射前后3.5 h内风速偏差为正偏差最大值、正偏差次大值、负偏差最大值、负偏差次大值作为研究个例，分析建模效果。研究个例的V1，V2随高度变化特征如图7所示。由图7a可见，7.5～12.0 km高度内V2明显大于V1，偏差为5.84～26.00 m·s-1，平均值为18.31 m·s-1，其他高度层的偏差则表现为正值、负值交替的变化特征。由图7b可见，大部分高度层的V1明显小于V2， 4.1～10.3 km高度内的偏差为5.1～14.0 m·s-1，平均值为8.88 m·s-1。由图7c可见，V2在大部分高度层均小于V1，3.3～12.0 km 高度内的偏差为-15.00～-6.00 m·s-1，平值均为-10.29 m·s-1。由图7d可见，2.5～16.0 km 高度内V2均明显小于V1，其他高度层则相反，7.1～13.0 km高度内的偏差为-21.00～-5.99 m·s-1，平均值为-14.94 m·s-1。

图7 火箭发射前后3.5 h内风速最大正偏差(a)、次大正偏差(b)、最大负偏差(c)和次大负偏差(d)的V1和V2变化特征Fig.7 Variation of V1 and V2 corresponding to the largest positive deviation(a),the second largest positive deviation(b),the largest negative deviation(c) and the second largest negative deviation(d) of wind speed within 3.5 hours before and after rocket launch

3.2 建模分析

WRF模式的初始场资料为08:00，设置模式输出预报产品的时间分辨率为15 min，水平分辨率为9 km，垂直方向1000 hPa至50 hPa分为48层。利用WRF模式可获取与研究样本(间隔3.5 h)时间一致的高空风预报场，该3.5 h内高空风预报差异以符号ΔVf表示(ΔVf=Vf2-Vf1,Vf1和Vf2分别为WRF模式得到的火箭发射前3 h和发射后0.5 h高空风预报)。利用V1和ΔVf，可得到火箭发射后0.5 h高空风预报Vf，

Vf=V1+ΔVf。

(6)

Vf即为火箭发射后0.5 h高空风预报。下面以高空风V2为基准，对高空风预报Vf的精度特征进行分析。

在整个高度范围内，3.5 h风速偏差为正偏差最大值、正偏差次大值、负偏差最大值、负偏差次大值所对应的V1，V2和Vf随高度变化特征见图8。由图8可见，与V1相比，Vf更接近V2。在图8a中，以V2为基准，V1和Vf的平均偏差分别为-6.51 m·s-1和-3.07 m·s-1，平均绝对偏差分别为7.72 m·s-1和5.08 m·s-1，平均相对误差绝对值分别为24.77%和21.17%，平均相关系数分别为0.91和0.96；在图8b中，V1和Vf的平均偏差分别为-5.93 m·s-1和-1.54 m·s-1，平均绝对偏差分别为6.41 m·s-1和3.18 m·s-1，平均相对误差绝对值分别为18.88%和10.19%，平均相关系数分别为0.97和0.97；在图8c中，V1和Vf的平均偏差分别为6.91 m·s-1和1.46 m·s-1，平均绝对偏差分别为7.25 m·s-1和2.95 m·s-1，平均相对误差绝对值分别为28.59%和12.98%，平均相关系数分别为0.93和0.97；在图8d中，V1和Vf的平均偏差分别为6.40 m·s-1和0.34 m·s-1，平均绝对偏差分别为7.09 m·s-1和1.62 m·s-1，平均相对误差绝对值分别为48.13%和12.69%，相关系数分别为0.92和0.99。以上相关分析均达到0.01显著性水平。由上述分析可知，与高空风V1相比，高空风预报Vf更接近高空风V2。

图8 火箭发射前后3.5 h内风速最大正偏差(a)、次大正偏差(b)、最大负偏差(c)和次大负偏差(d)的V1，V2和Vf变化特征Fig.8 Variation of V1, V2 and Vf corresponding to the largest positive deviation(a),the second largest positive deviation(b),the largest negative deviation(c) and the second largest negative deviation(d) of wind speed within 3.5 hours before and after rocket launch

从2014年12月—2020年12月共325组高空风样本中挑选火箭发射前后3.5 h内高空风差异最大的20%样本，该样本在整个高度范围内的平均绝对偏差为3.33～7.72 m·s-1。利用上述模型得到所选样本的Vf，同样以V2为基准，分别对V1和Vf的精度进行分析。V1和Vf的精度随高度变化特征见图9。对于风速偏差(图9a)，V1和Vf的偏差分别为-0.55～1.58 m·s-1和-1.54～1.05 m·s-1，平均值分别为0.50 m·s-1和-0.22 m·s-1。与V1的绝对偏差相比，Vf的绝对偏差明显偏小(图9b)，V1和Vf的绝对偏差分别为1.92～8.51 m·s-1和1.02～4.52 m·s-1，平均值分别为4.51 m·s-1和3.07 m·s-1。对于相对误差绝对值(图9c),V1和Vf的相对误差绝对值分别为7.79%～70.28%和7.18%～87.24%，平均值分别为25.39%和20.56%。图9d为V1和Vf的相关系数随高度的变化，分别为0.48～0.91和0.23～0.99，平均值分别为0.75和0.79。即利用模型得到Vf的偏差、绝对偏差、相对误差绝对值均偏小，相关系数偏大，表明相对于V1，Vf更接近V2。

图9 火箭发射前后3.5 h内高空风差异最大的20%样本的V1和Vf的偏差(a)、绝对偏差(b)、相对误差绝对值(c)、相关系数(d)随高度变化特征Fig.9 Variation of deviation(a),absolute deviation(b),absolute relative error(c),correlation coefficient(d) with height for 20% samples of V1 and Vf with the largest difference with 3.5 hours before and after rocket launch

采用类似的方法，依次挑选出3.5 h内高空风差异最小的20%样本，差异次小的20%样本，…，差异最大的20%样本(共5组)，分别记为资料1,资料2,…,资料5, 5组资料的V1，Vf与V2间的数理统计结果见表1，其中相关系数均达到0.01显著性水平。由表1可见，相对于V1，除资料1、资料2的Vf偏差略大外，其他情况下的Vf偏差、绝对偏差、相对误差绝对值均偏小，相关系数偏大，即Vf更接近V2。对比表1的数理统计结果可见，火箭发射前后3.5 h内高空风差异越大，Vf绝对偏差、相对误差绝对值减小更明显，即改进的效果越好。

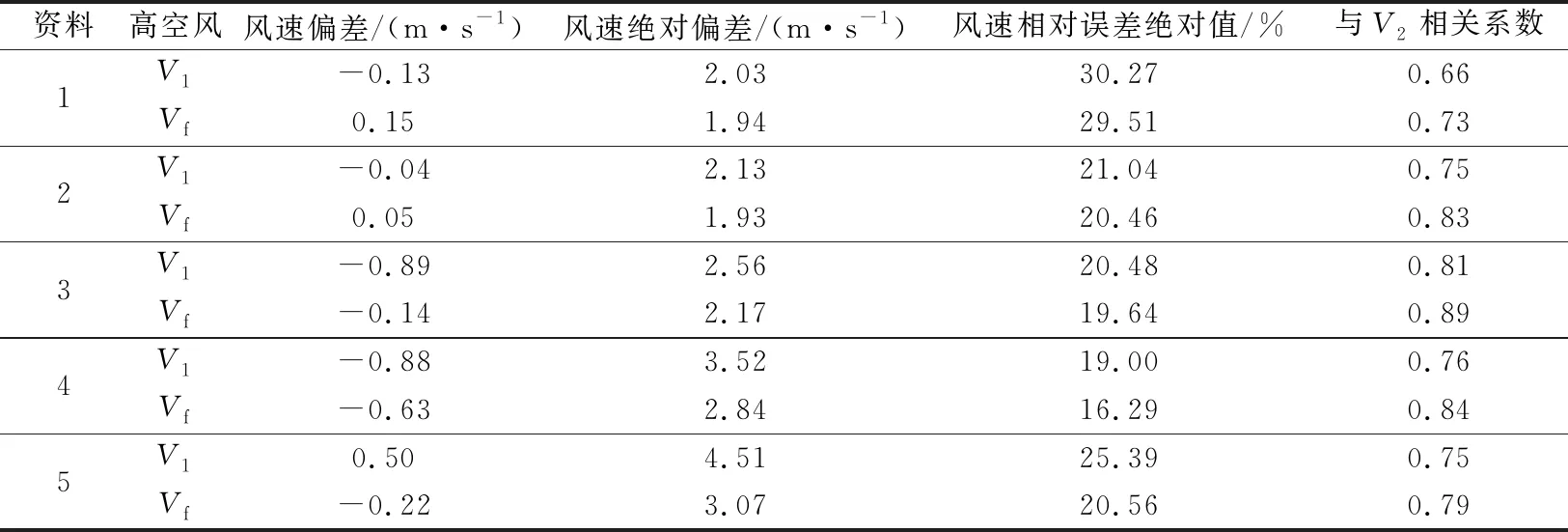
表1 资料1～资料5的V1,Vf与V2数理统计结果Table 1 Mathematical statistics between V1, Vf and V2 of data 1 to data 5

4 小 结

采用2014年12月—2020年12月间隔3.5 h高空风资料集对火箭发射前后3.5 h内的高空风差异进行统计分析，并利用WRF模式和V1建立火箭发射后0.5 h高空风预报模型，得到主要结论如下：

1) 火箭发射前后3.5 h内高空风速、风向偶尔会出现非常明显的差异特征，且该差异特征与高度层有关。在325组高空风样本中，高空最大风速偏差范围为-24.00～26.00 m·s-1，位于±10 m·s-1范围内占有率为68.30%，达到总数的三分之二，主要出现在对流层中高层的[6.5 km，11.5 km)高度(49.54%)。高空最大风向偏差范围为10.00°～180°，在[30°，60°)区间内占有率最高(28.31%)，主要出现在对流层中低层的[1.5 km，6.5 km)高度(68.92%)。

2) 火箭发射前后3.5 h内高空风速、风向差异特征与高度层有关。[11.5 km，16.5 km)高度的风速相对误差绝对值在[0，10%)的占有率和风向绝对偏差在[0°，10°)的占有率均明显高于其他高度层，对应的[1.5 km，6.5 km)高度则明显低于其他高度层。

3) 随着V1平均值增大，火箭发射前后3.5 h内风速绝对偏差表现为增大趋势，但相对误差绝对值和风向绝对偏差均表现为减小特征，且大部分高度层均表现出类似特征，说明高空风强时，风向不易发生短时变化。

4) 不同季节火箭发射前后3.5 h内高空风差异特征不同。冬季火箭发射前后3.5 h内风速绝对偏差较大、风速相对误差绝对值和风向绝对偏差较小，夏季火箭发射前后3.5 h内风速绝对偏差较小、风速相对误差绝对值和风向绝对偏差较大，鉴于冬季高空风较大、夏季高空风较小，火箭发射前后3.5 h 内高空风差异随季节变化与高空风的季节特征有关。

5) 与高空风V1相比，基于WRF模式和高空风V1建立模型得到的发射后0.5 h高空风预报Vf，在多种不同情况下均更接近高空风V2，且火箭发射前后3.5 h内高空风差异越大，模型订正的提升效果越明显。

通过上述分析可知，火箭发射前后3.5 h内高空风速、风向偶尔出现明显差异，且随V1平均值增大，火箭发射前后3.5 h内风速绝对偏差呈现增大趋势，考虑到V1平均值越大，越不利于火箭安全飞行，因此，若V1平均值较大(如超过30 m·s-1)，不建议以V1作为判断运载火箭能否安全飞行的依据。利用WRF模式和V1建模得到的Vf，在多种不同情况下均更接近V2，且火箭发射前后3.5 h内高空风差异越大，模型订正的提升效果越明显。因此，若以模型得到的Vf为判断依据，有利于降低决策风险，提高运载火箭的安全飞行保障能力。