穿越断层分段柔性接头隧道纵向地震响应解析解

闫高明， 赵伯明， 高 波， 王子珺

(1.北京交通大学 城市地下工程教育部重点实验室，北京 100044；2.北京交通大学 土木建筑工程学院，北京 100044；3.西南交通大学 交通隧道工程教育部重点实验室 土木工程学院,成都 610031)

随着我国交通建设技术的发展，交通基础工程向复杂地势、地形地区延伸，这些地区地震烈度高，活动断裂发育，如新建的川藏铁路、“一带一路”战略沿线的中亚D线、雅万高铁等重大工程就将穿越多条活动断层带，这就面临修建大量穿越活动断层隧道的严峻挑战。数次地震地震调查表明，隧道穿越断层位置是受震害最为严重区域之一[1-4]，隧道穿越断层处易发生拱顶坍塌、衬砌错台、路面隆起、衬砌裂缝等严重震害。因此，迫切需要开展穿越断层隧道抗减震技术方面的研究。

目前，对于穿越断层隧道抗减震技术的研究较少。隧道设置柔性接头使衬砌能够灵活适应断层施加的剪切变形，从而减小隧道主体结构的损坏，是一种有效抗减震措施[5-6]。针对柔性接头减震效果的现有研究较少，且主要采用数值分析、模型试验方法研究。Shahidi等[7]在隧道穿越断层处提出了柔性接头的设计方法，并采用有限元数值模型证明提出柔性接头能允许隧道纵向出现变形差异，减小隧道破坏。An等[8-12]也运用数值分析方法研究了分段柔性接头隧道的响应。Kiani等[13]采用离心机模型试验正断层作用下节段衬砌的响应，研究表明由于衬砌节段和接头足够的变形能力，衬砌结构损坏很小。闫高明等[14-15]设计了两种柔性接头形式，并通过振动台模型试验证明提出接头能够自身适应性变形协调减轻隧道结构震害，使衬砌震害的局部化。黄强兵等[16-21]都采用模型试验研究了分段柔性接头隧道的响应，结果表明隧道设置柔性接头避免了衬砌结构的应力集中，降低了衬砌本身的受力。尽管以上分析可以更好地考虑围岩-结构相互作用、围岩体的非线性等问题，但数值方法的计算量大、精度受多因素影响，模型试验需要消耗大量人力物力财力。

理论解析方法可以有效避免以上问题，是工程初步设计广为使用的方法，同时对于隧道抗减震机理分析方面有着数值法和模型试验不可替代的作用。隧道的纵向地震响应理论解析方法主要有自由场变形法和土结相互作用法[22]。土结相互作用法相比自由场变形法考虑了土与结构的相互作用，在工程设计中应用更为广泛。Yu等[23]基于弹性地基梁模型考虑了土-结构相互作用，推导了土岩变化地层隧道纵向地震响应的解析解。刘国钊等[24]采用Pasternak双参数弹性地基梁推导断层错动下隧道的纵向响应解析解。然而目前在穿越断层隧道柔性接头的理论解析方面鲜有研究。陈涛[25]建立了地层变化段隧道设置柔性接头的力学模型，其以扭簧等效模型模拟柔性接头，该模型是以允许衬砌节段在地震作用下发生相对扭转为前提的。地震作用下，穿越断层隧道常受到周围围岩的强制剪切位移。柔性接头的设计应该不仅能使隧道衬砌节段之间发生扭转，还应该允许其之间发生可控的位移差[22]。因此，如何建立合理的穿越断层隧道柔性接头力学模型及地震响应解析表达式，是指导穿越断层隧道柔性接头设计的坚实基础。

地震对穿越断层隧道的影响主要有两方面：断层错动引起的破坏和地震动引起的破坏。本文基于以地震动影响为主的穿越断层隧道，针对穿越断层隧道柔性接头无可用抗震设计方法的现状，首先建立了柔性接头力学简化模型，推导出穿越断层隧道柔性接头纵向地震响应的解析表达式，提出了穿越断层隧道柔性接头纵向抗震简化分析方法，然后验证了提出方法的有效性和可行性。最后在此基础上，结合给出的解析表达式分析不同参数对穿越断层隧道地震响应的影响规律。

1 力学模型与解析解

1.1 柔性接头力学模型

隧道穿越断层以及地层变化段，地震作用下断层发生错动或地层突变位置发生较大变形差异导致隧道发生较大变形，隧道衬砌可能会发生开裂、错台，甚至坍塌的严重震害。对于穿越断层隧道，设置柔性接头是一种有效的抗减震措施。设置柔性接头主要是允许隧道纵向在接头位置出现变形差异，从而释放地震动能量，避免衬砌结构的应力集中。因此，本文将柔性接头简化为一个垂直于隧道轴向的拉压弹簧和一个扭转弹簧的力学模型，即允许两个衬砌节段之间位移不连续和转角不连续，如图1所示。图1中，Cw为拉压弹簧刚度，CФ为扭转弹簧刚度。

图1 柔性接头力学模型Fig.1 Mechanical model of flexible joints

1.2 穿越断层隧道柔性接头力学模型

地震作用下，隧道穿越断层处易受到断层围岩对其的剪切作用，因此采用考虑了剪切变形的剪切梁模型模拟隧道衬砌节段。为获得某穿越断层隧道的地震动响应解析解，对该隧道模型如下假设：

(1) 将隧道穿越断层处简化为三个区域，分别为上盘、断层和下盘区域，每一个区域满足连续、均匀和各项同性的假定；

(2) 地震作用下断层未发生错动，隧道受地震动影响为主，隧道与围岩的相互作用通过弹性地基弹簧的形式实现，考虑断裂破碎带与上下盘围岩的性质不同，上盘、断层和下盘的地基弹性抗力系数分别为K1、K2和K3；

(3) 隧道简化为一段处于不同地层条件中的弹性地基上的剪切梁，该剪切梁模型考虑了隧道的横断面剪切变形的情况，衬砌除接头位置沿纵向满足连续性、均匀性和各项同性；

(4) 仅考虑地震震动对隧道的内力和变形增量的影响；

(5) 忽略初始地应力的影响。

安韶等[26]研究表明接头设置在上下盘与断层接触位置作用最显著。本文节段间采用提出的柔性接头力学模型连接，接头设置在上下盘与断层接触带位置，如图2所示。图2中，衬砌结构的抗弯刚度为EI，其中E为隧道衬砌的弹性模量，I为隧道横截面的惯性矩。

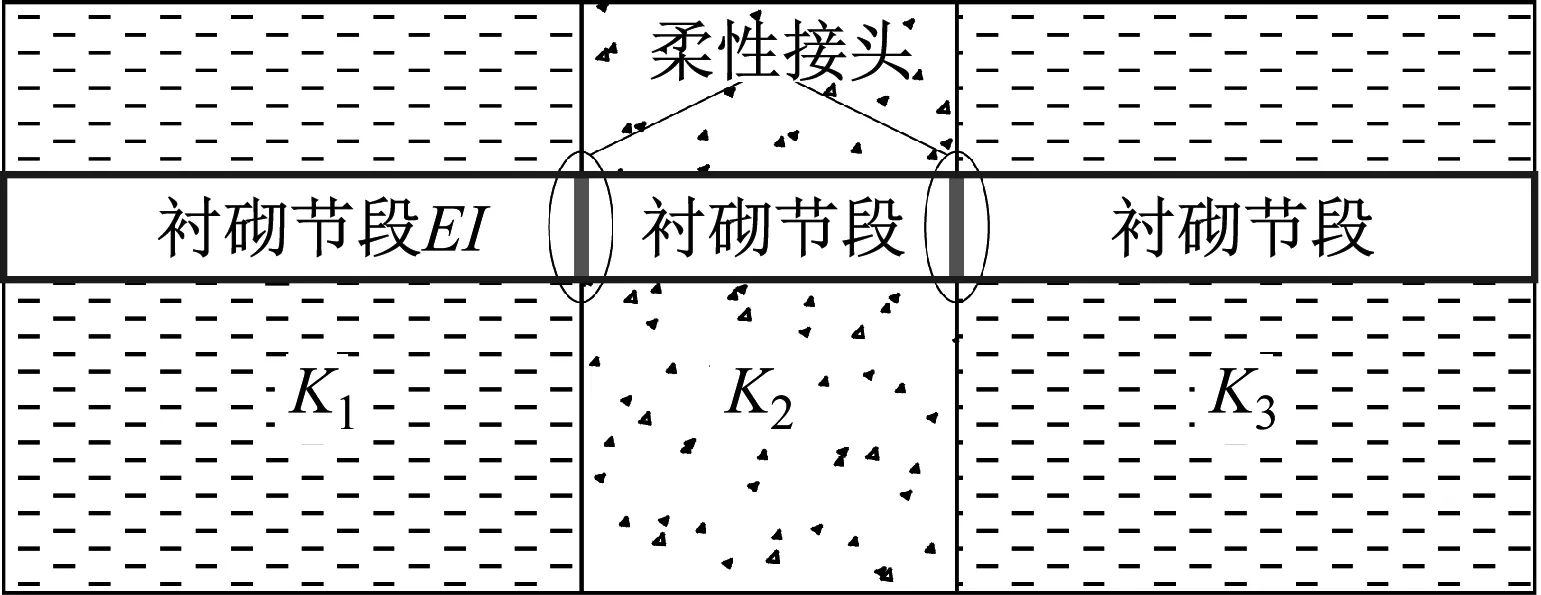
图2 穿越断层隧道简图Fig.2 Schematic of tunnel through fault

采用弹性地基上的剪切梁模型模拟隧道与围岩的相互作用，剪切梁的控制方程可表示为

(1)

式中:“′”表示变量对梁轴线位置x的导数;“··”表示变量对时间项t的导数;κ为剪切修正系数;G为剪切模量;A为横截面面积;φ为梁弯曲所引起的旋转角;μ为梁的单位长度质量，μ=ρA，ρ为梁的单位体积质量;K为地基弹性抗力系数;wg定义为隧道位置的自由场位移;w定义为隧道结构的位移。

1.3 梁纵向响应解析解

假定所受外荷载为简谐荷载wg(x,t)=Wg(x)·eiΩt，则位移和转角也分别可表示为

w(x,t)=W(x)·eiΩt

(2)

φ(x,t)=Φ(x)·eiΩt

(3)

式中:t为时间;Ω为荷载频率。

将以上表达式代入式(1)中，消去时间变量，方程可表示为

(4)

根据式(4)可得

(5)

为了简化方程，引入系数a1，a2，b1，b2，则该方程可简化为

(6)

式中，

式(6)的解析解可根据格林函数方法得到。根据格林函数的物理意义，G(x,x0)是以下方程的解

W″″+a1W″+a2W=b1δ″(x-x0)+b2δ(x-x0)

(7)

式中，δ(·)是狄拉克函数。

对式(7)进行求解，首先对式(7)左边右边做拉普拉斯正、逆变换和留数法，整理得到

(8)

式中，W(0)，W′(0)，W″(0)，W‴(0)可视为常数，可以通过梁的边界条件求得。φj(j=1,2,3,4,5)，ψi(i=1,2,3,4)分别为

(9)

(10)

式中，si(i=1,2,3,4)是s4+a1s2+a2=0的根。

根据叠加原理，可以得到式(6)的解析解为

(11)

则沿隧道纵向的弯矩和剪力由下式求得

(12)

(13)

1.4 穿越断层隧道纵向响应解析解

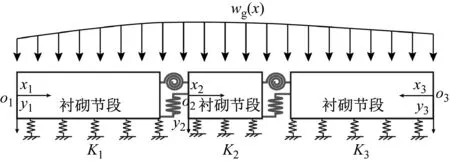
图3 穿越断层隧道力学模型Fig.3 Mechanical model of tunnel through fault

根据以上推导过程可发现，格林函数的代数表达形式相对比较固定，各段衬砌的格林函数具有统一的形式，因此各段衬砌的格林函数可假定为

Gi(x,xi0)=H(xi-xi0)φi1(xi-xi0)+Aiφi2(xi)+

Biφi3(xi)+Ciφi4(xi)+Diφi5(xi)(i=1,2,3)

(14)

结合现有文献研究[27]，模型两端取为自由边界，即两端边界弯矩和剪力均为0

(15)

在衬砌节段之间，隧道的位移、转角、弯矩和剪力满足以下条件：

在上盘与断层衬砌连接处和在下盘与断层衬砌连接处分别为

(16)

(17)

将式(14)和(15)代入式(16)和(17)可得到

(18)

式中,具体参数表达式见附录A。

通过式(18)可以求解各待定系数的值，则3段衬砌的格林函数就得到了。以上求得的是各节段在局部坐标系上的格林函数，将局部坐标系换为整体坐标系，令

x0=x0,x1=x,x20=x0-L1,x2=x-L1,

x30=L-x0,x3=L-x，则穿越断层隧道衬砌的格林函数为

G(x;x0)=

(19)

根据格林函数的定义可知，外荷载作用下衬砌的位移响应可由式(11)得到，各节段衬砌的内力可由式(12)和(13)得到。

2 模型验证

依托典型的穿越断层隧道，隧道进口位于康定县雅拉乡三道桥村，出口位于康定县瓦泽乡318国道附近。该隧道穿越折多山。隧道穿越折多塘断裂、金龙寺-磨子沟断层等，隧址区地震活动性强。隧道洞身净断面设计为：该隧道近圆型，洞宽14.40 m，洞高13.46 m。衬砌采用C35钢筋混凝土，衬砌厚度60 cm。隧道横断面采用外接圆半径法[28-29]，采用外接圆半径法可确定内直径为12.66 m，外直径为13.86 m，其它具体力学参数如表1所示。结合现有文献研究[30]，柔性接头刚度取为ζ=Cw/κGA=CФ/EI=0.05。隧道穿越断层位置峰值加速度为0.4g，场地地震波的加速度时程如图4所示。

表1 隧道衬砌力学参数Tab.1 Mechanical parameters of the tunnel lining

图4 地震波加速度时程图Fig.4 Acceleration time-history curve of earthquake wave

根据隧道周围地层信息可得，隧道断层位置的剪切波速为Vs1=301 m/s，上下盘位置围岩的剪切波速为Vs2=563 m/s，地震波波长Lwave=156.89 m。需要说明的是，为了分析方便，文中的波长假定为断层处地震动主频对应的波长，实际应用可以取不同的波长进行参数化分析，给出实际地震动对应的一个计算范围，通过解析解给出包络曲线来指导实际工程设计。地基视为线弹性，其地基弹簧系数可根据式(20)得到[31]

(20)

式中:ρ为岩土体密度;Vs为土体剪切波速;ν为岩体泊松比;d为隧道直径;Lwave为地震波波长。

由式(20)可得断层的地基系数为Kb1=336 MPa，上下盘的地基系数为Kb2=1 151 MPa。隧道所在位置的自由场位移峰值通过场地分析软件Deepsoil[32]得到：上下盘的自由场位移峰值为wmax1=0.031 m，断层位置的自由场位移峰值为wmax2=0.099 m。因此，可得到断层自由场位移和上下盘的自由场位移如下式[33]

(21)

式中，α0为位移函数相位角，通过改变α0实现位移波形沿隧道纵轴的平移，从而模拟行波效应。

结合典型隧道工程，上下盘长度取L1=L3=80 m，断层破碎带宽度为L2=40 m。地震波入射角取为θ=0°，相位角α0=0°。

2.1 与有限元结果对比

利用有限元软件ANSYS建立模型，采用总长为200 m的梁单元模拟隧道结构，单元网格为0.5 m，模型两端采用自由边界；采用离散的弹簧单元模拟柔性接头模型和地基弹簧，其中地基弹簧间隔与梁单元间距保持一致，将自由场的正弦波形位移施加到地基弹簧非连接结构端，数值模型参数保持与解析解一致，从而得到有限元的数值解。

采用本文方法与有限元数值模拟方法分别计算穿越断层隧道的地震响应。图5～8分别给出了上述工况下隧道结构的位移响应、转角响应和内力响应。实线表示本文提出方法结果，虚线表示有限元数值结果，灰色阴影部分表示断层破碎带区域，横坐标ξ表示隧道纵向位置与全长的比值。

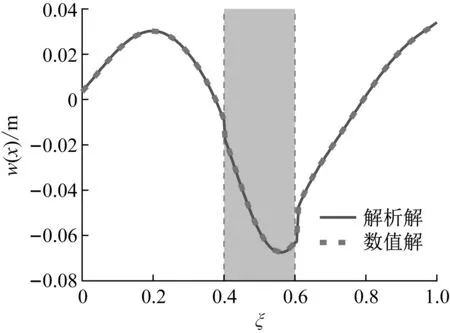
图5 隧道结构的位移响应Fig.5 Displacement of tunnel

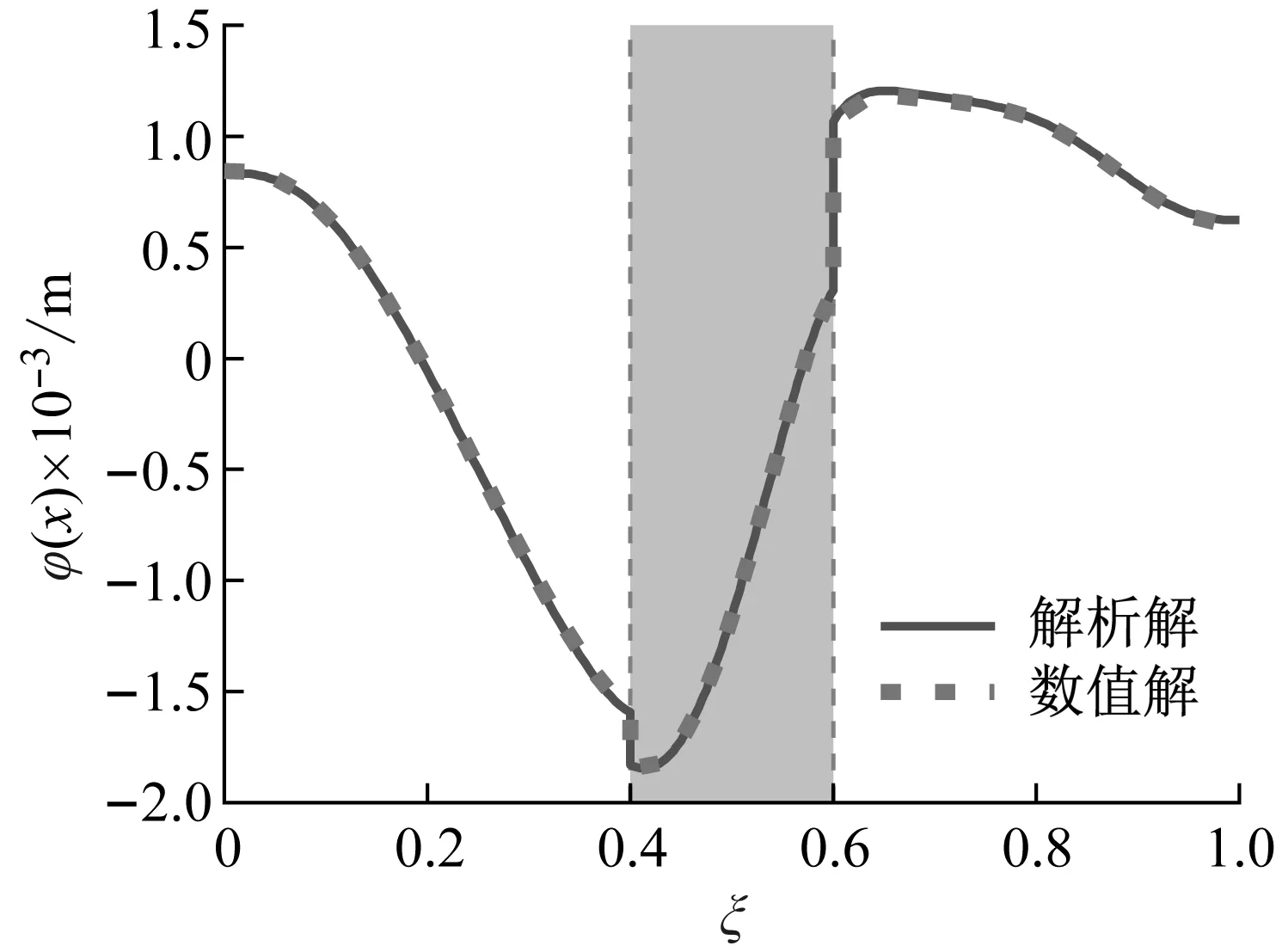
图6 隧道结构的转角响应Fig.6 Rotation angle of tunnel

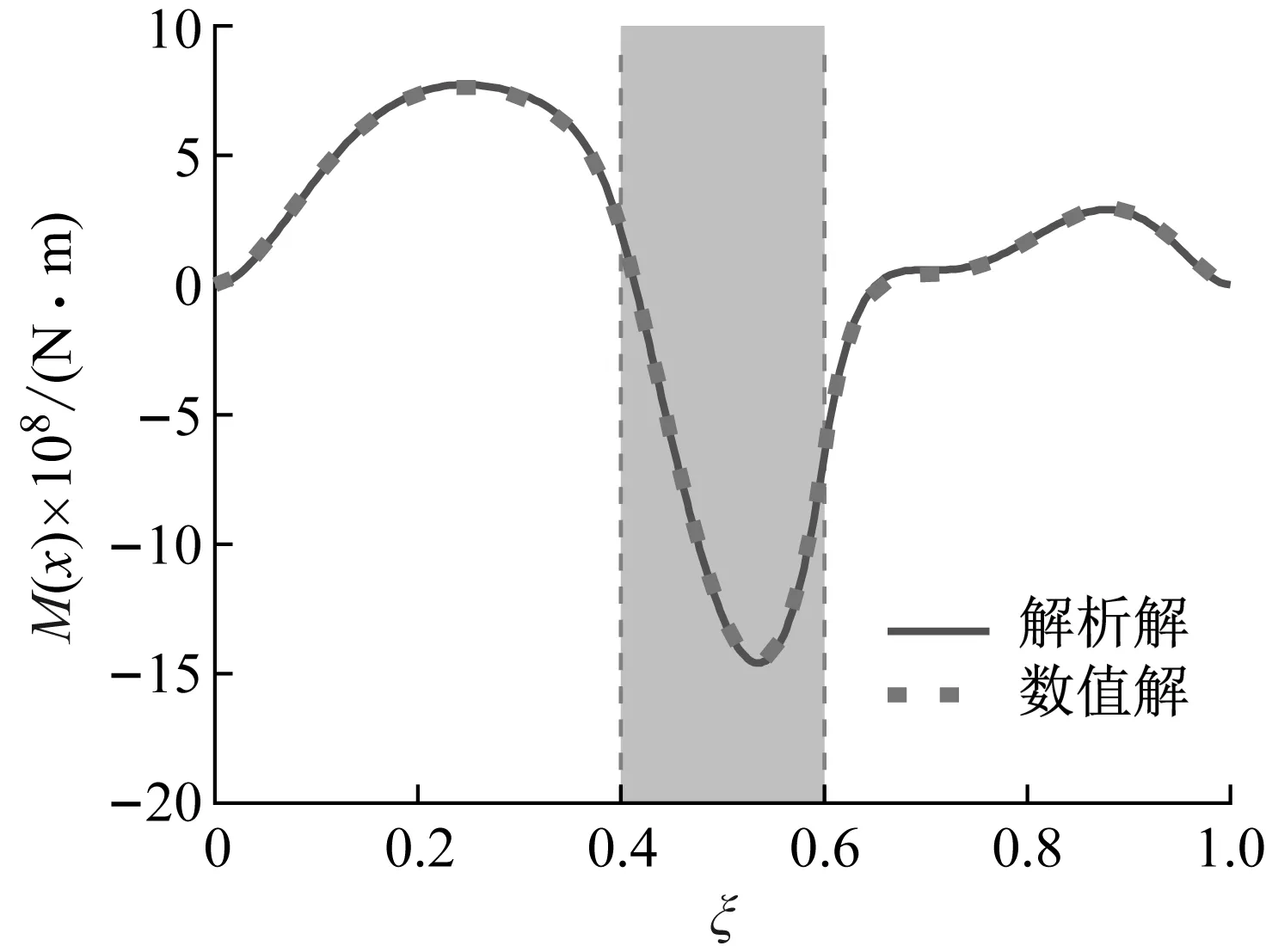
图7 隧道结构的弯矩响应Fig.7 Bending moment of tunnel

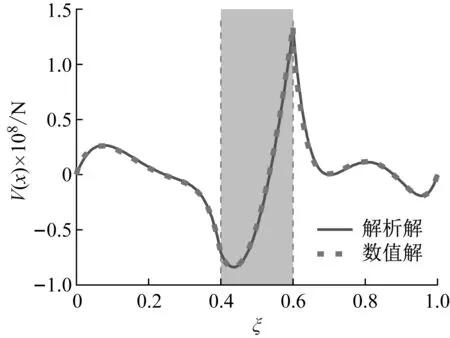
图8 隧道结构的剪力响应Fig.8 Shear force of tunnel

通过对比本文方法的解析结果与有限元结果可以看到，本文的解析解与有限元数值解吻合较好，说明了采用格林函数推导的穿越断层隧道柔性接头的纵向地震响应解析解具有较高的计算精度。

如图5和图6所示，隧道衬砌在两接头位置都出现了位移差和转角差，如表2所示，与预期的效果相同。由于柔性接头的设置，衬砌在两接头位置分别产生0.83 cm和1.54 cm的位移差以及0.000 24 rad和0.000 76 rad的转角差，这使得衬砌结构能够较好地适应围岩不均匀变形的影响，从而使地震动对隧道衬砌的不利影响局部化。

表2 衬砌在两接头位置的位移差和转角差Tab.2 Differences of displacement and angle of the lining at the two joint

由图5～8可以看到，断层位置隧道的地震响应明显大于上下盘位置衬砌的响应，这主要是由于断层处围岩相对较弱，受地震动影响较大，衬砌的位移响应大，衬砌与围岩相互作用力大，使衬砌的内力响应值较大。同时可以发现，断层中部位置衬砌的弯矩值最大，剪力的最值分布在断层与上下盘接触面位置，是隧道抗震设防需要重点关注的区域。

2.2 与既有研究对比

为了验证本文解的合理性，将本文解与已有文献 [25] 的解析解进行对比。图9～图12对比分析了不同接头类型对隧道衬砌位移响应的影响。其中文献[25]提出的接头模型是将柔性接头简化为一可扭转的弹簧模型，将本文接头模型的拉压弹簧刚度设置为0即可退化为该模型。如图9～图12所示，与文献[25]的曲线变化趋势基本相同，说明了本文提出接头模型的正确性。设置本文提出接头类型衬砌的位移曲线和转角曲线在接头位置附近明显与现有文献的接头形式以及未设置接头衬砌的位移响应和转角响应不同，同时其位移响应峰值大于另两种接头类型的位移响应，这主要是由于本文接头模型既可允许隧道发生位移差又可发生转角差，这与刘学增等[34]的试验结果以及Hashash等提出的柔性接头设计理念相同，这也说明了本文提出接头的合理性。在接头位置x=120 m处，设置提出接头衬砌的位移响应在接头左侧大于另两种接头类型的位移响应，而在接头右侧的位移响应却小于另两种接头类型的位移响应，这说明体现了柔性接头使断层对隧道动力响应影响局部化的设计思路。

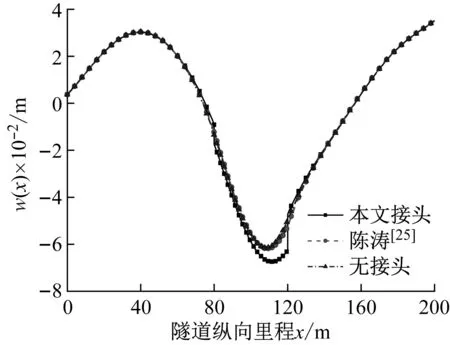
图9 不同柔性接头类型隧道的位移响应Fig.9 Displacement of tunnel with different joint type

图10 不同柔性接头类型隧道的转角响应Fig.10 Rotation angle of tunnel with different joint type

图11 不同柔性接头类型隧道的弯矩响应Fig.11 Bending moment of tunnel with different joint type

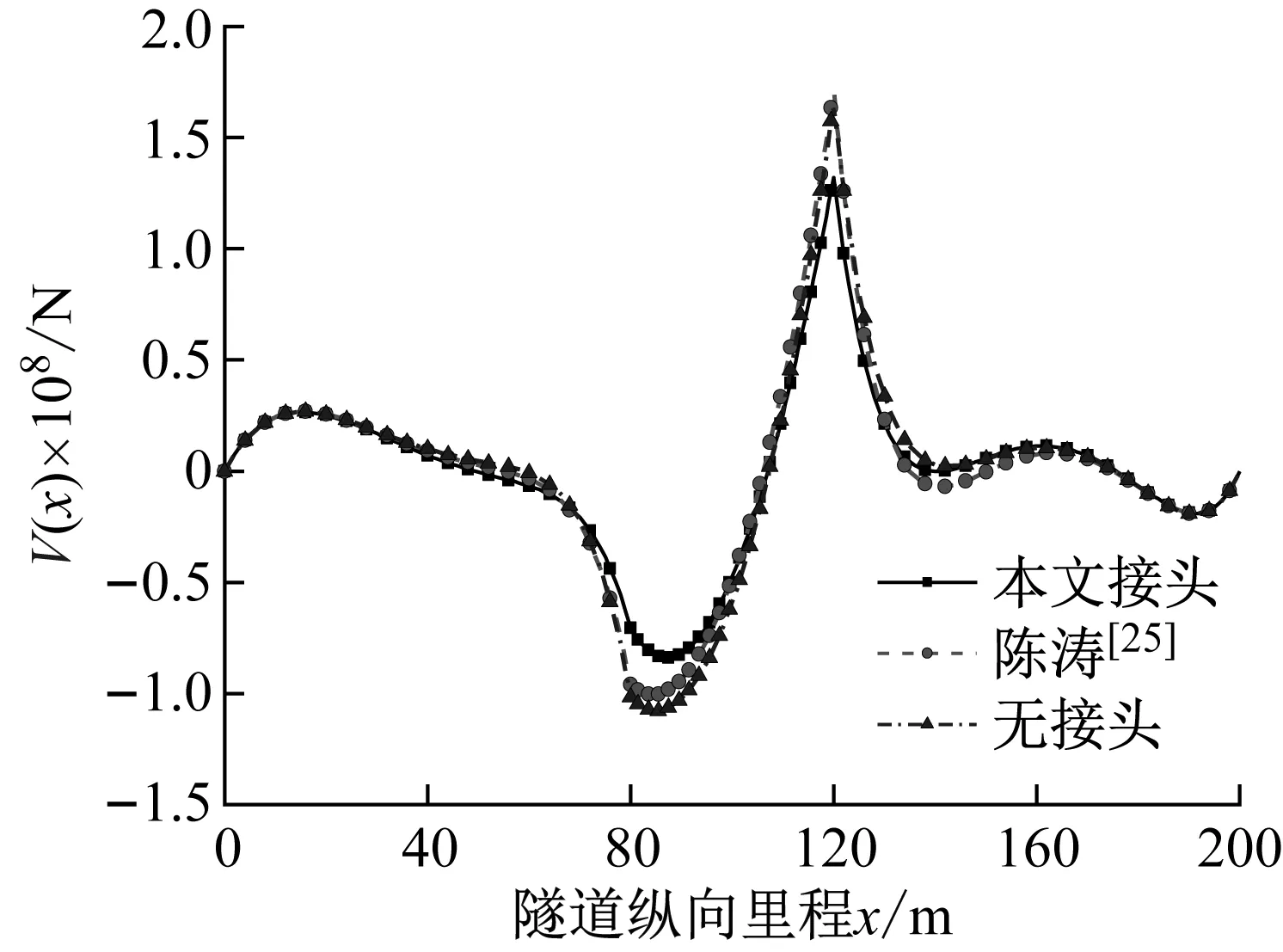
图12 不同柔性接头类型隧道的剪力响应Fig.12 Shear force of tunnel with different joint type

从图11中可以看到，设置提出柔性接头模型的衬砌弯矩响应最小，而连续衬砌弯矩响应最大，其最大值比本文提出接头模型大30.14%，衬砌剪力也有相同的变化规律。因此，设置本文接头模型衬砌内力明显比连续衬砌和设置扭簧接头衬砌的内力小，这也说明本文接头模型的有效性。同时可以看到提出接头的设置对隧道衬砌的影响范围在x=50～130 m，使衬砌的弯矩响应明显减小。图11中，三种工况的弯矩响应曲线的最大值都出现断层位置，这说明无论是否设置接头，穿越断层隧道弯矩的不利位置主要在断层中部和断层与上下盘接触面区域，是抗震设防需重点关注的区域。

由图12可以看到，三种工况的剪力响应极大值都主要位于两接头位置处衬砌，这也说明无论是否设置接头，穿越断层隧道的剪力不利位置主要在断层与上下盘接触带位置。设置提出接头模型的剪力最大值均小于其它形式的剪力最大值，其值比衬砌之间刚性连接的剪力最大值减小了20.24%，而设置扭簧接头衬砌的剪力最大值比连续衬砌的剪力最大值减小3.24%。同时可发现设置本文提出接头模型的衬砌的剪力响应在x=60 m～130 m范围内比其它形式衬砌的剪力响应小。

3 参数敏感性分析

在以上验证算例的基础上，本节主要通过对比隧道沿纵向的位移、内力来阐述结构刚度和断层宽度对穿越断层分段柔性接头隧道结构地震响应的影响。需要说明的是，本节的参数敏感性分析都是基于上述数值验证算例，在保证其它参数变化的情况下，仅改变某一参数，研究某一独立参数对隧道结构地震响应的影响规律。

3.1 结构刚度的影响

调整刚度加固衬砌是一种常见的抗震措施，它的设计思路是提高隧道自身的抗震性能。图13～图15中EI为依托工程的衬砌弯曲刚度，本节计算中令全长隧道衬砌弯曲刚度相同，选取隧道衬砌的弯曲刚度分别为EI、2EI、4EI、6EI、8EI，保持接头刚度不变，研究不同衬砌刚度对穿越断层隧道衬砌地震响应的影响。

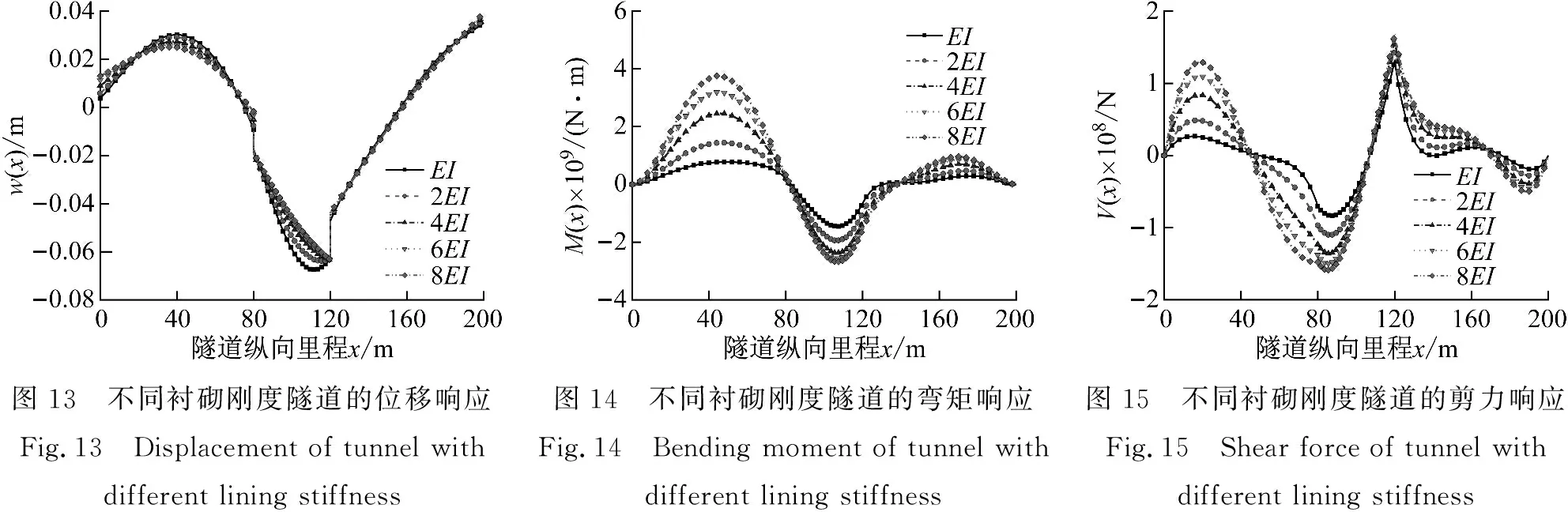
由图13可知，衬砌弯曲刚度为2EI的位移最大值比衬砌弯曲刚度为EI的值减小5.34%，衬砌弯曲刚度为4EI的位移最大值比衬砌弯曲刚度为2EI的值减小0.73%，而衬砌弯曲刚度为6EI的位移最大值比衬砌弯曲刚度为4EI的值仅减小0.02%，因此隧道衬砌弯曲刚度增大，衬砌的最大位移响应值减小，但减小的幅度明显减小。同时可发现, 在x=120 m接头位置，衬砌弯曲刚度为2EI的位移差比衬砌弯曲刚度为EI的值增大12.13%，4EI的衬砌位移差比2EI的衬砌位移差增大8.07%，而6EI的衬砌位移差比4EI的衬砌位移差增大3.19%，在x=80接头位置位移差也有相同的变化规律。因此衬砌弯曲刚度越大，其在两接头位置的位移差越大，即接头所承担的位移越大，这说明结构刚度越大，接头的作用越明显。图14对比分析了不同隧道衬砌刚度下衬砌的弯矩响应，衬砌弯曲刚度为2EI的弯矩最大值比衬砌弯曲刚度为EI的值增大33.28%，衬砌弯曲刚度为4EI的弯矩最大值比衬砌弯曲刚度为2EI的值增大22.00%。故衬砌弯曲刚度的增大使衬砌的弯矩显著增大，这对隧道的安全是不利的。不同弯曲刚度的隧道剪力响应与弯矩响应有相同的变化规律，如衬砌弯曲刚度为2EI的剪力最大值比衬砌弯曲刚度为EI的值增大12.13%。

3.2 断层破碎带宽度的影响

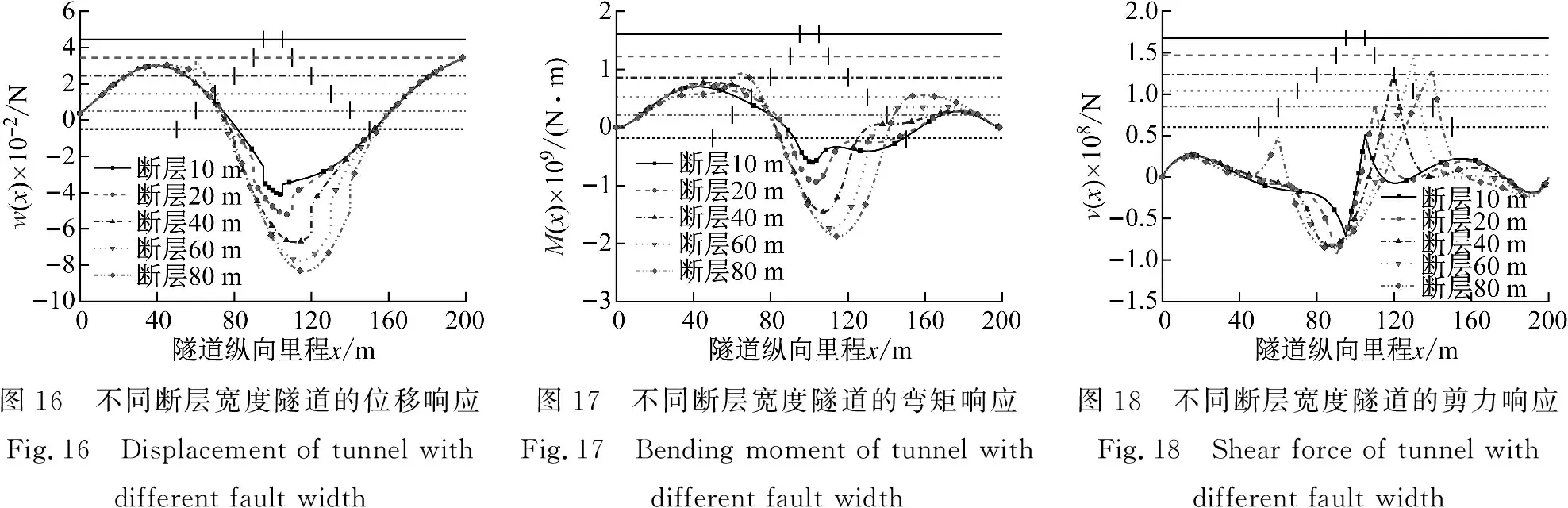
隧道穿越断层破碎带处衬砌受地震动影响很大，是隧道震害最严重的区段，本节主要探究不同断层破碎带宽度对隧道结构地震响应的影响。

图16～图18中竖直短线表示不同断层宽度的位置。由图16可知，地震动作用下，不同断层宽度条件下衬砌的位移响应最大值均出现在断层位置处。断层宽度为40 m的位移最大值比断层宽度为20 m的位移最大值增大29.27%，断层宽度为60 m的位移最大值比断层宽度为40 m的位移最大值增大14.94%，断层宽度为80 m的位移最大值比断层宽度为60 m的位移最大值增大7.60%。因此随着断层破碎带宽度的增大，隧道的位移响应最大值也随之单调增大，但增加幅度减小。进一步可发现，断层的宽度越大，其对隧道位移沿轴向的影响范围也越大。如图17和图18中所示，各个工况衬砌的弯矩响应曲线变化趋势都比较一致，且弯矩响应最大值都位于断层中部位置；不同断层宽度的衬砌剪力响应曲线在断层中部、断层与上下盘接触带位置出现极值点，这与汶川地震震害调查结果相同[35]。断层宽度为40 m的衬砌弯矩最大值比断层宽度为20 m最大值增大54.40%，断层宽度为60 m的衬砌弯矩最大值比断层宽度为40 m的最大值增大19.16%，断层宽度为80 m的衬砌弯矩最大值比断层宽度为60 m的衬砌最大值增大7.66%。整体上随着断层宽度的增加，衬砌的弯矩最大值增大，但增加幅度减小。对于剪力而言，断层宽度为20 m的剪力最大值比断层宽度为10 m的最大值增大30.65%，断层宽度为40 m的剪力最大值比断层宽度为20 m的最大值增大42.01%，断层宽度为60 m的剪力最大值比断层宽度为40 m的最大值增大9.11%，而断层宽度为80 m的剪力最大值比断层宽度为60 m的最大值减小9.79%，因此剪力最大值随断层宽度增大表现为先增大后减小的趋势。同时可发现，在隧道设置柔性接头情况下，断层宽度增大，其对隧道内力沿轴向的影响范围也增大。

4 结 论

针对以地震动影响为主的穿越断层隧道，本文建立了穿越断层分段柔性接头隧道纵向简化力学模型，提出了相应的定量抗震简化分析方法。以有限元数值解为基准，对比相同工况下的结构响应，验证了提出方法的有效性和可行性。在此基础上，结合本文给出的解析表达式分析了不同参数对穿越断层分段柔性接头隧道地震响应的影响规律，主要得出以下结论：

(1) 本文的解析解与有限元数值解吻合较好，说明推导的穿越断层分段柔性接头隧道的纵向地震响应解析解具有较高的计算精度。由于提出柔性接头模型的设置，隧道衬砌在两柔性接头位置既出现了位移差，又出现转角差，使衬砌结构能够较好地适应断层围岩不均匀变形的影响，减小其对衬砌的损害，与预期效果相同。

(2) 柔性接头能增大衬砌的可允许变形能力，从而有效减小隧道衬砌的内力，使断层对隧道动力响应影响局部化。无论是否设置接头，穿越断层隧道受力的不利位置主要分布在断层中部和断层与上下盘接触面位置，是抗震设防需重点关注的区域。

(3) 对于穿越断层隧道，增大衬砌的弯曲刚度会减小衬砌上的位移响应值，也增大其在两接头位置的位移差，同时会显著增大衬砌上的内力响应值，因此不能一味地以增加衬砌的弯曲刚度来抵抗地震动。

(4) 地震动作用下，不同断层宽度条件下衬砌的位移响应最大值均出现在断层中部位置处。随着断层破碎带宽度的增大，整体上隧道的位移响应最大值也随之增大，衬砌的弯矩响应最大值也增大，而剪力响应最大值表现为先增大后减小的趋势。在设置柔性接头情况下，断层宽度增大对隧道地震响应沿轴向的影响范围仍增大。

文中提出的穿越断层设置接头隧道的纵向响应分析方法可定量得到工况下隧道在接头位置产生的位移和转角以及内力，这为工程中柔性接头的参数设计提供参考。具体工程中柔性接头刚度参数的确定，可先通过提出的理论方法计算接头不同刚度参数下隧道的响应，然后根据具体工程允许的内力和变形以及静载条件的要求等因素综合确定最优的接头刚度参数，从而进一步指导柔性接头设计。需要指出的是，由于理论方法围岩弹性等假定，对新提出方法的实际工程应用后续还需做进一步深入研究。

附录A

(A.1)

(A.2)

(A.3)

(A.4)

(A.5)

(A.6)

(A.7)

(A.8)

(A.9)

(A.10)