盾构穿越复合地层机体振动影响因素研究

朱建才,邓智宝,袁逢逢,袁宗浩,王 哲

(1.浙江大学 平衡建筑研究中心,浙江 杭州 310012;2.浙江工业大学 土木工程学院,浙江 杭州 310023;3.中铁隧道股份有限公司,河南 郑州 450001;4.浙江大学 建筑设计研究院有限公司,浙江 杭州 310000)

盾构法以工期短、安全性高和劳动强度低等优势,已在城市地下隧道建设中得到广泛应用,然而在盾构隧道距离既有建筑比较近的情况下,盾构施工对周围环境的影响不可忽略。在开挖盾构隧道过程中，由于地层因素和施工因素会对地层造成不可避免的扰动并破坏原有的平衡状态,周围地层和地面应力状态会发生改变,从而产生变形,严重时还会造成地面塌陷;此外,采用盾构法施工还会因刀盘和掌子面地层的切削作用产生振动,这种振动会对隧道周围土体产生影响,甚至透过地基传递至邻近建筑物,对建筑物内居民和高精度仪器等产生影响[1]。目前,针对地铁盾构方面的研究主要集中在施工开挖过程中的变形问题,缺乏对盾构施工过程中机体振动及其影响因素的深入研究。研究人员采用不同的方法来探究盾构隧道施工对周围地层应力、变形的影响规律。现阶段常用的方法主要有理论分析法、数值计算法等。

在简化的理论计算模型方面,Peck公式是研究地表沉降规律的热点,沈培良等[2]依据上海某盾构施工地面沉降观测数据,分析了地表沉降槽经验公式的适用性,并提出了其参数的确定方法;韩煊等[3]在盾构引起地表沉降的基础上,研究了隧道开挖对邻近建筑结构的变形影响,提出了高斯分布模型并验证了模型的有效性。然而现有研究方法对地层损失的界定尚有不足之处,因此王建秀等[4]对地层损失的概念进行了重新界定并建立对应模型。数值计算法是另一种分析盾构施工对周围环境影响的有效方法,盾构施工环境影响主要体现在隧道开挖引起地下土层的损失并在地表处产生沉降,沉降变形与施工过程中注浆压力、掌子面总推力和盾构收缩等施工因素有关,有限元方法能够有效灵活地计入上述影响因素,其中地层损失是造成地层变形的主要因素[5-7]。除了施工控制参数因素,影响地表沉降的还有地质条件,李小青等[8]模拟了盾构施工造成地层损失的过程,分析了影响地表沉降的主要地质影响因素,包括隧道埋深、内摩擦角等,并在预测地表变形的基础上提出了控制地表沉降的措施。在城市地下空间开发的新时期,城市地下隧道也将面对更加复杂的施工条件,地下交叠隧道便是其中之一,孙钧等[9]对交叠隧道施工进行了模拟,得到了地表沉降的最大值会在盾构机掘进后产生陡增的结论。盾构施工对邻近建筑物变形影响是另一个重要工况,刘波等[10]分析了隧道工程下穿已有建筑基础引发变形的空间效应规律,并提出了应提高注浆体强度的建议;丁祖德等[11]结合深圳某地铁下穿住宅小区工程,分析了不同隧道与建筑基础交汇角度对建筑物结构变形的影响,得出了不同交汇角度对建筑结构变形影响明显,但对结构内力影响较小的结论。盾构施工的环境影响研究问题还包括:当盾构机在城市地下地层中掘进时,由于刀盘和掌子面地层的切削作用,会造成盾构机体振动上升,这种振动影响不仅作用在掌子面上,而且会对隧道周围土体产生影响,甚至透过地基对邻近建筑结构和人群产生不良影响,目前针对该方面的研究相对较少。随着盾构隧道施工离城市振动敏感区域越来越近,关于隧道振动对周围环境影响的研究也愈显重要,隧道振动主要分为运营阶段振动和施工阶段振动。目前针对盾构振动对环境影响的研究主要集中在地铁运营阶段产生振动环境影响，刘维宁等[12]研究表明：轨道交通列车轮轨间相互作用是列车产生振动的主要原因,振动通过轨道基础、衬砌结构和地层传播到周围土体和地表是列车振动影响周围环境的主要方式[13-15];丁智等[16-18]通过数值模拟、室内试验和现场测试等方法对列车运营振动进行了深入研究,得出了隔振的有效措施。在隧道的施工阶段也会产生振动响应,不同于运营阶段因为轮轨作用而产生的交通振源振动,盾构隧道在施工过程中的振源振动主要来源于刀盘切削岩层时产生的不均匀接触压力导致的盾构机体振动。目前,针对盾构施工阶段振动影响的研究较少,起步也较晚,王鑫等[19-21]用数理统计和现场实测相结合的方式,分析了施工阶段地层条件和盾构机主要施工参数对振源振动的影响,该研究针对单一软土或者硬质地层。城市地层分布中上软下硬复合地层较为常见,上软下硬复合地层中上部为强度和刚度较小的软土地层,下部为强度及刚度较大的硬质地层或者岩石,目前尚缺乏针对上软下硬复合地层的盾构机体振动影响因素研究。当盾构穿越上软下硬复合地层时,开挖面上下部分岩土体力学特性差异较大,刀盘切入硬岩破碎时产生较大的机体振动,因此笔者采用现场测试的方法,通过对比盾构隧道在软土地层和上软下硬复合地层掘进时的振动差异,分析盾构机体振动的主要影响因素,同时通过灰关联熵分析法及多元线性回归分析法获得了盾构机体振动的主要影响因素,研究成果可为优化盾构施工参数,减小隧道开挖对地层的振动提供工程参考。

1 工程概况

拟建杭州市某城市道路改建工程是杭州市快速路系统中的一段,是杭州市内连接多个中心市区的东西向重要地下城市道路,地下隧道包括明挖段和盾构段,其中盾构段自东向西穿越多条市区中心重要路段及地铁2号线。盾构开挖直径为13 m,纵断面呈“V”形,隧道长度约1.7 km。该隧道掘进起点埋深为6 m,终点埋深为13 m,最大埋深为24 m,隧道主要穿越地层为砂质粉土、中等风化凝灰岩、全风化凝灰岩和软土层,盾构施工掘进时掌子面不仅通过全断面软土地层,还通过上部为软土地层、下部为坚硬岩层的上软下硬复合地层,两种地层强度差异明显。南北线地质剖面图如图1所示,盾构施工范围内的主要地层分布如表1所示。

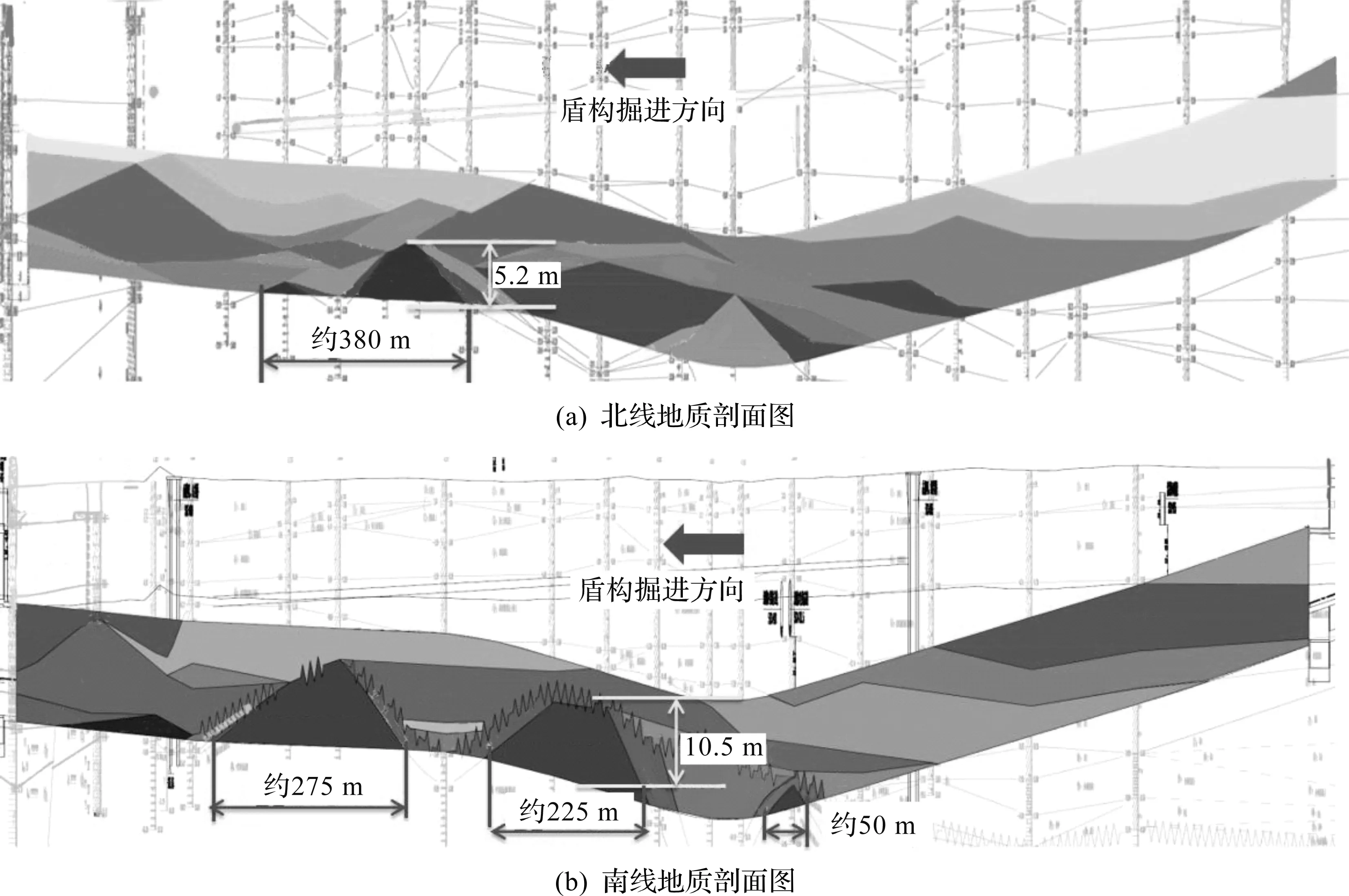
图1 盾构隧道地质剖面图Fig.1 Strata profile along the tunnel longitudinal direction

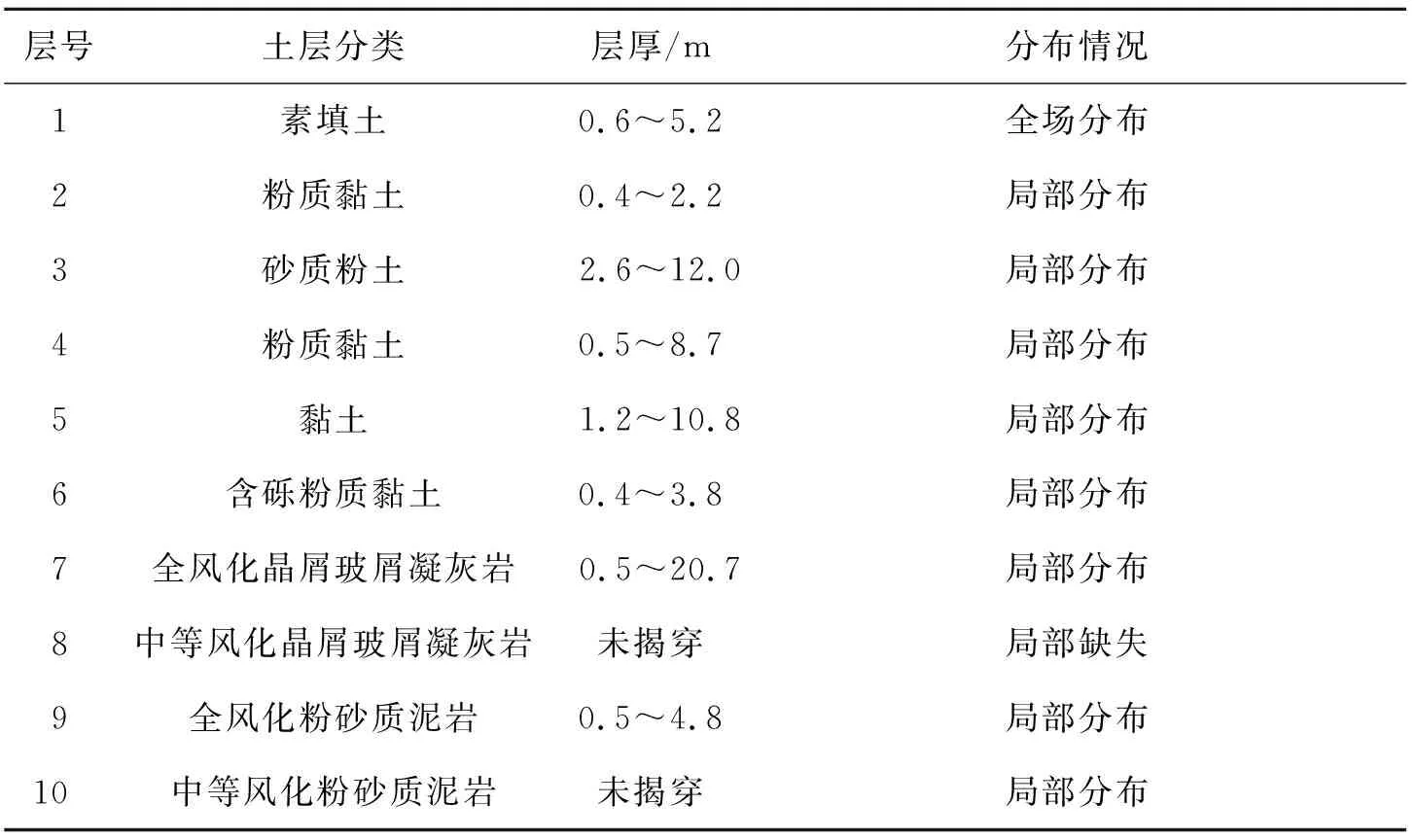
表1 施工范围内地层分布Table 1 The soil layers within the tunnel construction scope

2 现场测量仪器和方案

2.1 测量仪器

现场测量仪器采用高精度振动测试系统(包括数据采集仪及传感器等),其中硬件包括941B(新)型速度传感器、INV3062C 24位网络分布式采集分析仪以及高性能笔记本电脑。数据采集和分析软件为DASP-V11工程版。

2.2 测量方案

为了研究不同地层条件和施工参数下盾构机体的振动规律,现场振动测试时依据施工纵断面中各个区域不同的地质情况,选取若干个上软下硬复合地层以及一般软土地层作为测试断面,同时为了分析不同地质条件的影响,在考虑上软下硬复合地层时着重讨论了硬岩在隧道开挖掌子面的占比对隧道机体振动的影响。在选定测试断面之后,根据盾构机体的实际情况,选取能够全面反映盾构机体振动响应水平的监测点,以获得较可靠的振源监测数据。振动测试结果中,测点X方向为盾构机掘进方向,Y方向为竖直方向,Z方向为与盾构机掘进方向正交的水平横向。测点布置如图2所示,测点仪器安装图如图3所示。

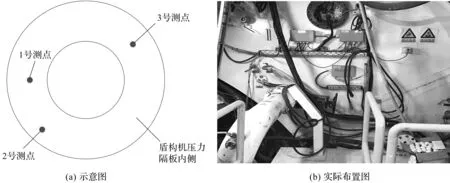
图2 测点布置示意图Fig.2 The measuring point layout

图3 仪器安装图Fig.3 Installation of instruments for the vibration test

2.3 测试工况

为了分析软土和上软下硬复合地层中盾构机体振动的主要影响因素,选取地层条件和盾构施工参数作为参考变量。考虑盾构机体振动主要受地层刚度影响,在分析地层条件影响时选取隧道埋深和掌子面平均动弹性模量为主要地层条件参数,盾构掘进参数有:掘进总推力、推进扭矩、推进速度和刀盘转速。依据地质勘探信息获取压缩模量,并通过模量转化和加权平均计算得到掌子面平均动弹性模量,具体计算步骤如下:首先,通过地勘报告和施工图获取各监测断面地层分布、层厚、泊松比和压缩模量;然后,通过公式计算各地层的弹性模量,并通过经验公式[22]计算动弹性模量;最后,以掌子面各地层的厚度为权重,通过加权平均计算各监测断面平均动弹性模量。依据各个施工断面实际掘进参数获得盾构施工参数。掌子面岩石占比是地层条件的主要影响参数之一,定义为掌子面中硬岩层厚与掌子面直径的比值。依据图1确定各测试断面地层分布,搜集施工参数,具体如图4和表2所示。弹性模量与压缩模量关系式为

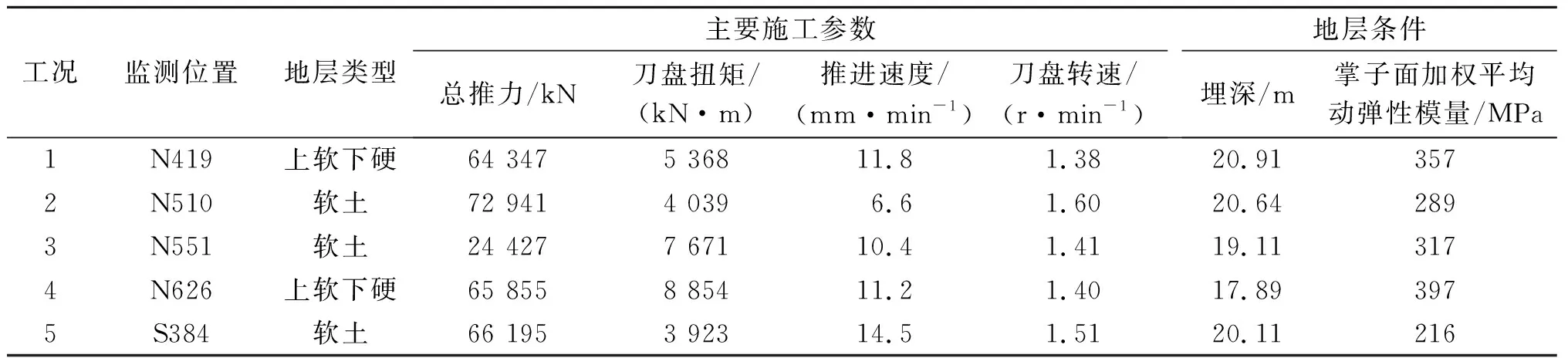
表2 不同断面隧道施工参数Table 2 The tunnel construction parameters for different cross section

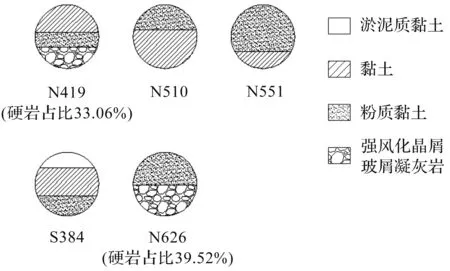
图4 作业面地层分布图Fig.4 The soil/rock components for the composite ground

(1)

式中:ES为压缩模量;μ为泊松比;E为弹性模量。

3 盾构机在不同地层掘进时机体振动分析

表3,4为盾构机在软土地层和上软下硬复合地层中掘进时机体三向振速峰值。从表3可以看出:在软土地层中,各测点Y方向(竖向)振速峰值为三向振速中的最高值,X方向与Z方向振速峰值相当。以竖向振速峰值为例,对比不同测点Y方向振速峰值可知:2号测点的竖向振速峰值普遍为3个测点中的最大值,1号测点次之,3号测点最小,而振速峰值在上软下硬地层中比在软土地层中升高显著。与软土地层相比,盾构机在上软下硬复合地层中掘进时,上部软土地层在刀盘切削作用下较容易发生破坏,土屑流动形态为流动型或断裂型[23],而下部硬岩由于强度和刚度较大、土层整体性较好,导致刀盘与硬土层的接触压力不均,岩石发生脆性破坏,进而使刀刃底部受到较大的激振力,从而引起刀盘和盾构机体整体振动水平的大幅升高。造成不同测点振动差异的原因如下:1) 测点与盾构机刀盘之间的距离,相较于1,2号测点,3号测点与盾构机刀盘的距离较远,1,2号测点与盾构机刀盘距离相当;2) 2号测点附近受到电子转机的影响,而1,3号测点周围环境比较简单,盾构机体振动的主要因素是盾构机刀盘转机的转动及刀盘、掌子面岩石的切削,2号测点周围的机械情况比较复杂,该测点附近有较多的转子机械,这会造成盾构机体振动的局部增大,这种局部增大是由于机械发动机高速转动引发的,不过对盾构机体的整体振动影响不大。以上是造成盾构机体各个测点振动数据差异的原因,总体上看，虽然现场复杂的因素造成了不同测点振动响应的局部差异,但盾构机各测点的振动影响处于同一水平。

表3 软土地层盾构机体三向振速峰值Table 3 The peak value of three-direction vibration velocity of shield machine in soft soil

表4 上软下硬复合地层盾构机体三向振速峰值Table 4 The peak vibration velocity of shield machine in upper soft and lower hard strata

为对比软土地层和上软下硬复合地层的盾构机体振动差异,选取1号测点为典型分析测点,在时域和频域内对比软土地层和上软下硬复合地层盾构机体振动响应的差异,结果见图5。由图5可知:机体振动中竖向(图5b)振动响应大于轴向(图5a)和横向(图5c)振动响应;盾构机在软土地基中掘进时机体竖向振动的振速峰值为0.1～1.0 mm/s,在上软下硬地基中掘进时机体振动的峰值振速为0.4～2.0 mm/s。在上软下硬复合地层中,由于岩层等刚度较大材料的存在导致机体振动显著升高,这是因为相较于软土这种强度和刚度较小的材料,岩石这种硬质材料刚度大,盾构掌子面切削时与岩石的动力相互作用大,同时硬质材料相较于软质材料阻尼更小,从而导致复合地层的机体振动显著升高。从频谱分析来看,不论在软土地层还是上软下硬复合地层,盾构机体的振速峰值主要分布在0～30 Hz,这部分频率主要对应于盾构机体刀盘旋转等引起的低频振动,在60～100 Hz时还可以观察到高频振动,这部分频率主要对应于盾构机体发动机转子。从频域中也可以观察到上软下硬复合地层三向速度响应均大于软土地层,这与时域中的结果一致。

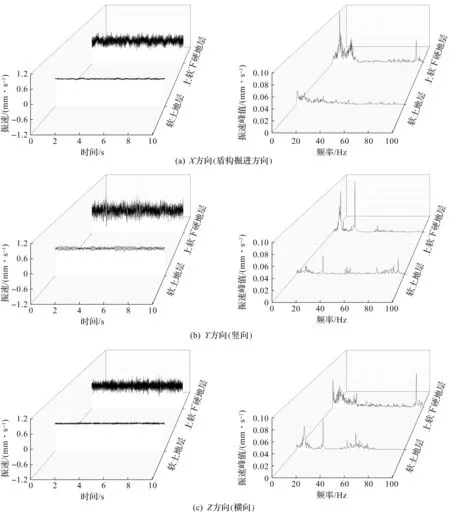
图5 1号测点软土地层和上软下硬地层测试结果分析图Fig.5 Analysis of the test results of the soft ground and the upper soft and lower hard ground at the No.1 measuring point

4 盾构机体振动影响因素分析

为了分析盾构机体振源振动的影响因素,考虑地层条件和施工参数对盾构机体振源振动的影响。地层条件包括掌子面平均动弹性模量和隧道埋深,盾构掘进参数有推进速度、扭矩、总推力和转速。为分析以上参数对盾构机体振动的影响,需要引入数理统计方法,因为现场测试条件的多变性,不同测试断面不仅隧道埋深、掌子面地层情况有所差别,而且盾构机的掘进速度、扭矩、总推力和转速,甚至现场作业环境等也不尽相同,所以采用控制变量法来分析盾构机体振动的影响因素有一定的困难。因此参照王鑫等[19-21]采用的灰联熵分析法和多元线性回归分析法来分析本研究工程案例中盾构机体振源振动的影响因素。

4.1 灰关联熵分析法

选取典型测点的振动响应峰值,采取灰关联熵分析法分析盾构机体振速的关键影响因素并对其进行排序[19-21]。灰关联熵分析法是分析复杂的多变量系统影响因素的有效方法,在控制变量法所需信息不足时可以采用这种方法进行分析。

灰关联熵分析法的分析步骤如下:确定映射量,并将映射量依据原始值进行无量纲化,映射量的无量纲化采用均值处理法实现,即将数列中的每个值都除以数列均值,得到一组新的无量纲化数列。

计算灰关联系数[19-21],即

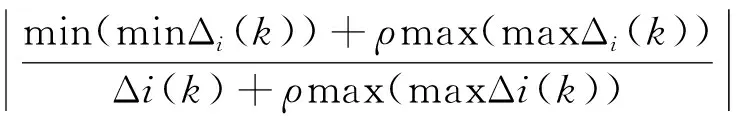
(2)

式中:Δi(k)=|x0(k)-xi(k)|(k=1,2,…,n;i=1,2,…,m);ρ为分辨系数,取值为[0,1],可取0.5;min(minΔi(k))为极差最小值;max(maxΔi(k))为极差最大值。

关联系数反映的是两点间的距离,关联系数位于区间[0,1]。

计算灰关联密度[19-21],即

(3)

式中:Pk为灰关联系数分布映射,是分布的密度值,Pk>0,且∑Pk=1。

计算灰关联熵和灰熵关联度,即

(4)

E(xi)=H(Ri)/Hmax

(5)

式中:H(Ri)为灰关联熵;E(xi)为灰熵关联度;Hmax=lnn,n为数值列的最大元素数量值。

由灰关联熵定理可知:熵关联度值较大者,与参考列的联系程度更密切。利用灰关联熵分析法分析施工参数及地层条件与机体振速的关系,设自变量为掌子面平均动弹性模量、掘进速度、盾构机扭矩、盾构机总推力、转速和埋深,因变量为盾构机机体的三向振动,并假设因变量的变化都是源自自变量的改变,选取已有测试断面开展灰关联熵分析法分析,断面图如图4所示,测点位置选取典型测点1。由灰关联熵分析法可知:灰熵关联度越接近于1,说明该自变量(地层条件、施工参数)对因变量(机体振速峰值)的影响越大。振源影响因素分析结果见图6,从图6可以看出:作业面测点Y向振速对不同施工参数和地层条件的关联性排序自大到小依次是:掌子面平均动弹性模量、盾构机扭矩、盾构总推力、盾构转速、埋深和掘进速度。因此对机体振动影响最大的地层条件是掌子面平均动弹性模量,对盾构机体振动影响较大的施工参数主要包括盾构机扭矩和总推力,而影响较小的是盾构转速埋深与掘进速度。

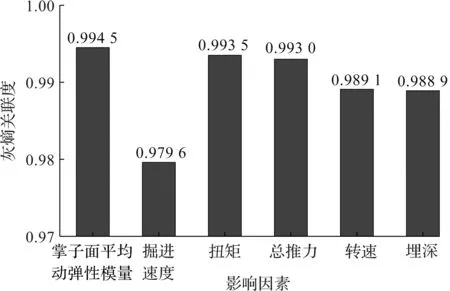
图6 振源影响因素分析Fig.6 Analysis of the main influencing factors

4.2 多元线性回归分析法

采用多元线性回归分析法进一步验证灰关联熵分析法的正确性。多元线性回归分析法被广泛用于分析社会经济领域变量之间的影响关系。多元线性回归分析的基本原理是:在一个客观系统中,一件事物的产生往往由多个因素引发,客观事物的联系错综复杂,虽然可以了解到结果与影响因素之间的因果关系,但是现象的变化往往是两个或多个因素共同作用的结果,此时就无法直观地感受到影响因素之间的主次关系。为了全面地了解这种由多因素引发的事物之间的客观联系,科学准确地评价现象之间的数量变动,并提高预测和控制变量的精确度,需要运用多元线性回归分析模型进行系统性分析。

通过回归分析可以建立不同变量之间关联性的数学表达式,在盾构机因掘进而产生的机体振动分析中,可用回归分析建立因变量(机体振速峰值)与自变量(影响因素包括地层条件和主要施工参数)间的数学表达式,即数学回归方程,并利用该数学回归方程评价影响因素对因变量的贡献度。

利用多元线性回归分析法分析盾构机体振动的影响因素,首先要建立机体振动幅值与影响因素之间关系的数学模型[19-21],即

Y=b0+b1X1+b2X2+b3X3+
b4X4+b5X5+b6X6

(6)

式中:Y为因变量(典型测点竖向振速),X1～X6分别为影响因素中的掌子面平均动弹性模量、盾构机掘进速度、扭矩、总推力、转速和埋深。

通过线性回归编程计算程序可以得到盾构施工掘进时振动振源的多元线性回归分析结果,相关系数R计算结果见表5,偏回归系数计算结果见表6。由表5可知:多元线性回归方程的相关系数R为0.95,接近于1,说明线性回归方程的拟合效果良好[19-21]。

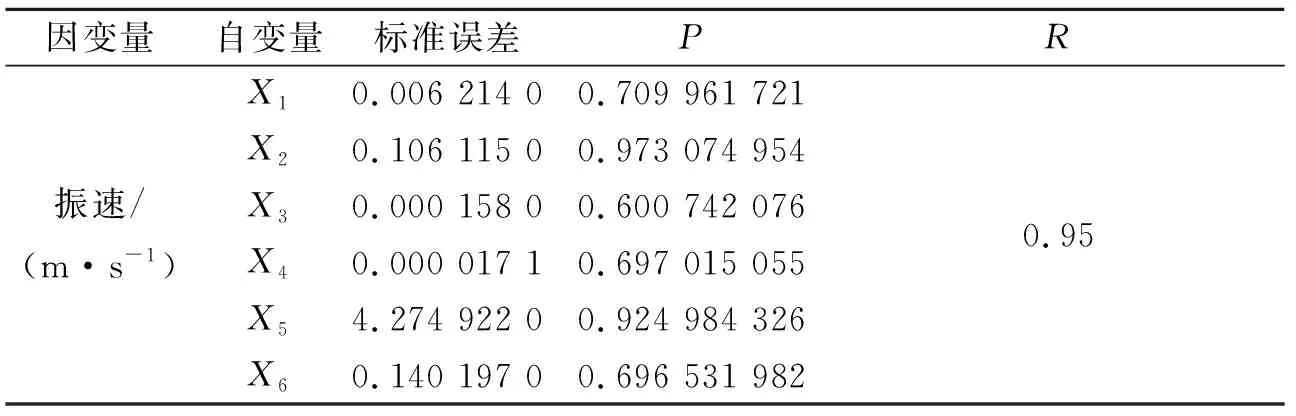
表5 盾构掘进施工影响因素多元线性回归分析Table 5 The multiple regression analysis of influencingfactors for the shield tunneling vibration

表6 竖向振动速度回归方程系数Table 6 The vertical vibration velocity regression equation coefficient

偏回归系数b体现了不同比较量和参考量的关联度高低,然而在通常情况下其本身的大小并不能反映其相对重要性,这是因为不同的自变量具有不同的量纲,所以必须要对偏回归系数进行标准化处理。回归系数的标准化公式为

(7)

式中:P为标准化的偏回归系数;X为自变量;Y为因变量。P越大表示对应自变量的相对重要度越高。偏回归系数标准化后结果如表7所示。以1号测点竖向振速峰值为例,针对影响盾构机体振动的地层条件和施工参数开展多元线性回归分析,由表7可知:掌子面地层条件及施工参数所对应的标准化偏回归系数P1>P3>P4>P5>P6>P2,这说明掌子面加权动弹性模量对机体振动贡献最高,其余排序自大到小依次是:盾构机扭矩、总推力、转速、埋深和掘进速度。这与灰关联熵分析法得出的结论一致,两种方法可相互印证。

表7 竖向振动速度回归方程标准化回归系数Table 7 The vertical vibration velocity regression equation standardized regression coefficient

4.3 主要地层因素对盾构机振动水平的影响

为了分析地层条件对盾构机体振动水平的影响,以掌子面加权平均动弹性模量为主要影响因素,以1号测点竖向振源振动峰值为因变量绘制如图7所示的关系曲线。从图7可以看出:当掌子面的动弹性模量小于350 MPa时,掌子面地层为软土地层,盾构机体的振源振动并未随着掌子面地层动弹性模量的增长而明显提高,而是处于上下波动的状态;当掌子面的加权动弹性模量大于350 MPa时,盾构机体振源振动将随着加权动弹性模量的增加显著升高,此时掌子面地层为上软下硬地层,这表明上软下硬地层中盾构机体的振动水平显著增大。

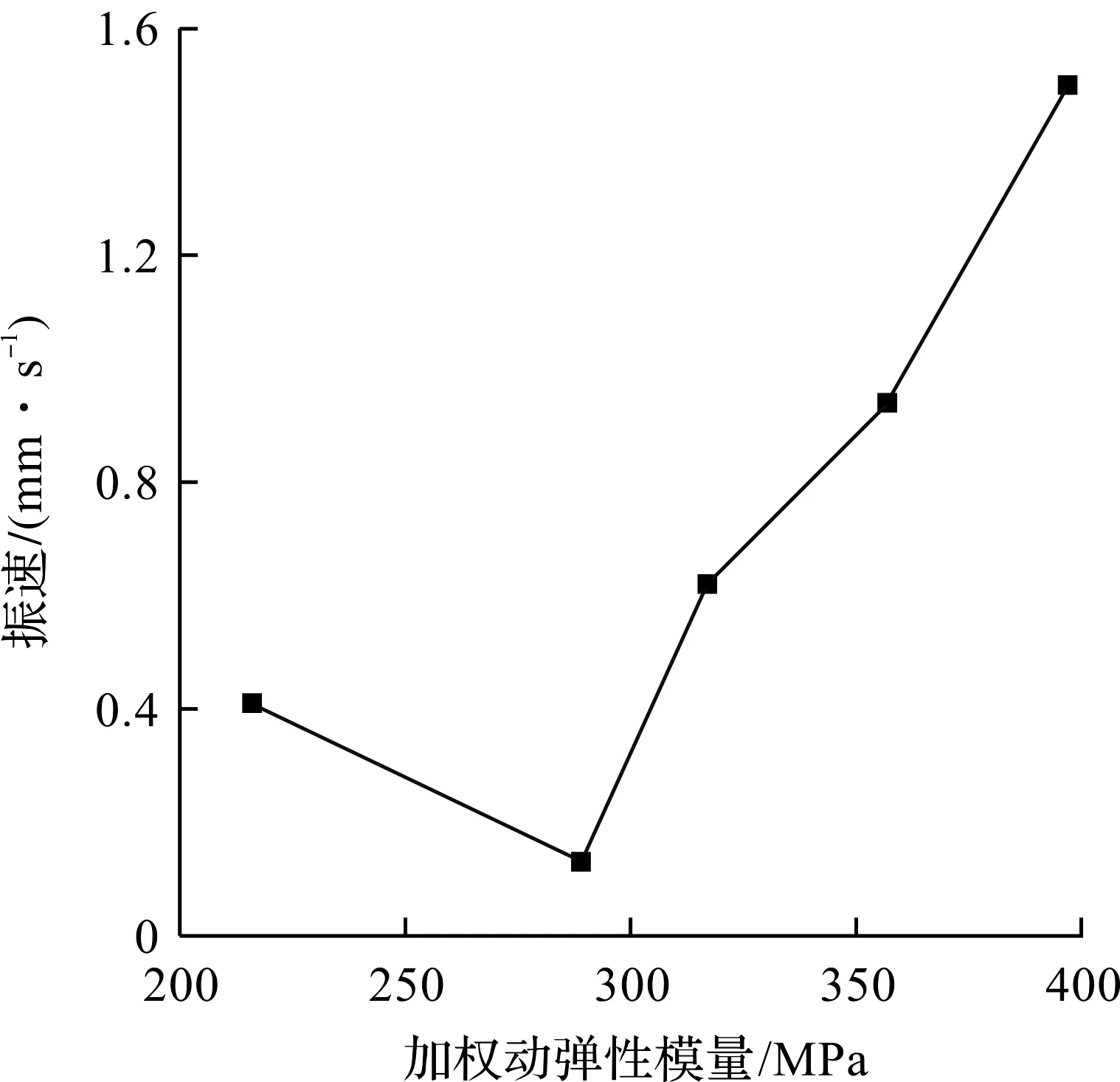
图7 加权动弹性模量与盾构机体振动峰值关系曲线Fig.7 The vertical velocity of shield tunneling machine versusthe modulus of the ground

为了更直观地展现掌子面地层构造对盾构机体振动水平的影响,以掌子面硬岩比例为横坐标,竖向振动峰值为纵坐标绘制如图8所示的关系曲线。从图8可以看出:随着掌子面硬岩占比的增加,机体振速也随之上升。当地层为软土地层时,机体振速增幅变化较小,当岩层占比进一步上升到30%～40%时,机体振速快速上升,这说明当硬岩占比大于30%时对盾构机体的振动影响非常显著。

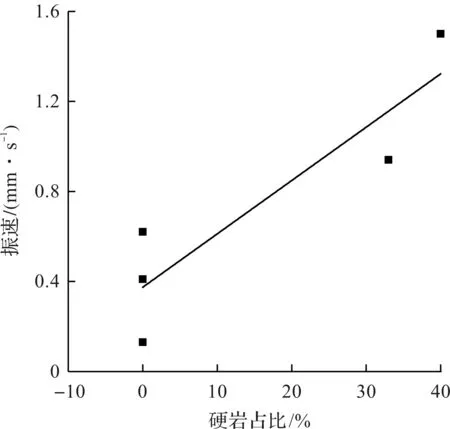
图8 掌子面硬岩占比与盾构机体振速关系曲线Fig.8 The vertical velocity of shield tunneling machine versusthe ratio of the hard rock at the tunnel face

5 结 论

以浙江省杭州市某城市道路改建工程为背景,选取盾构机在软土地层和上软下硬复合地层中掘进时的典型断面,分析了地层条件(掌子面平均动弹性模量、埋深)和施工参数(盾构机扭矩、盾构总推力、盾构转速和掘进速度)对盾构机体的振动影响,并采用灰关联熵分析法和多元线性回归分析法筛选出了影响盾构机体振动的主要参数,分析了盾构机体穿越软土地层和上软下硬复合地层振动响应的差异,得出以下结论:1) 软土断面和上软下硬断面盾构机体振动时程曲线和幅频特性近似,对比各个测点3个方向振速可知,竖向振速普遍比纵向、水平向振速要大;2) 软土地层盾构机的机体振速为0.1～1.0 mm/s,上软下硬复合地层的机体振速为0.4～2.5 mm/s,各测点频域峰值低频段为0～30 Hz,高频段为60～100 Hz;3) 盾构机在上软下硬复合地层掘进时,由于掌子面动弹性模量的增大,三向振速峰值有显著增加趋势;4) 盾构机振动响应对不同因素的关联性排序自大到小依次是:掌子面平均动弹性模量、盾构机扭矩、盾构总推力、盾构转速、埋深和掘进速度;5) 在上软下硬复合地层中减小盾构机扭矩是控制机体振动的最有效措施,其次是控制盾构掘进时的总推力,盾构转速、埋深对盾构机体振动影响有限。