基于深度学习的城市快速路交通流预测方法
2022-07-14高华兵舒文迪
高华兵,舒文迪,刘 志
(1.宜春职业技术学院 信息工程学院,江西 宜春 336000;2.浙江工业大学 计算机科学与技术学院,浙江 杭州 310023)
交通流预测可以获得未来的交通流状态,在路径引导、交通管控和交通信息服务等方面具有重要的意义[1]。在路径引导方面,交通流量预测能够为车辆路径规划提供重要参考,帮助出行者更好地选择路线;在交通管控方面,交通流量预测能够发现未来可能会发生拥堵的地点和时间,帮助管理者将资源分配到容易发生拥堵的道路上,最终缓解交通压力;在交通信息服务方面,交通流量预测能够帮助人们更好地使用商业车辆[2]。
时间序列分析模型采用曲线拟合和参数估计的方法预测交通流信息,其中最典型的方法是自回归积分移动平均(ARIMA)[3],ARIMA模型以自回归模型和滑动平均模型为基础,添加了积分环节,以消除时间序列中的短期波动。周晓等[4]基于卡曼滤波理论预测了道路的速度。近年来,深度神经网络已成为研究热点[5],然而随着城市道路感应设备布置范围增大,识别精度提升,许多深度学习模型被提出并用于解决交通流预测问题[6]。栈式自编码神经网络(SAE)[7]采用分层贪婪算法获取交通流的时空特征。循环神经网络能够利用记忆单元处理任意长度的输入,因此被广泛应用于短时交通流预测,在其基础上衍生的长短时记忆神经网络(LSTM)、门控循环单元(GRU)[8]表现出较好的预测性能。Tian等[9]使用LSTM对交通流进行预测,不仅获得了时间序列观测值的长期和短期依赖关系,而且利用缺失模式改进了预测结果。Wang等[10]将交通时间序列分解为趋势序列和残差序列,并使用LSTM分别进行预测,最后综合预测值得到结果。Zheng等[11]提出使用基于注意力机制的卷积LSTM神经网络提取交通流的时空维度的特征,并结合双向LSTM模块提取交通流的长期特征。目前也出现了许多关于图卷积神经网络(GCN)的研究[12-14]。基于上述研究成果,笔者提出通过基于时间聚类的交通流量预测模型TC-ConvLSTM来提升交通流预测的精度。
1 框架概述
基于深度学习的交通流量预测模型首先通过快速路上安装的微波检测器收集原始的流量数据;其次是预处理环节,对数据进行清洗,去除异常点;再次采用K-shape聚类方法对时序数据进行聚类,使用卷积LSTM神经网络对不同的簇进行训练,卷积LSTM神经网络同时考虑了交通流的时空特征,能够提升交通流预测的精度。模型架构如图1所示。
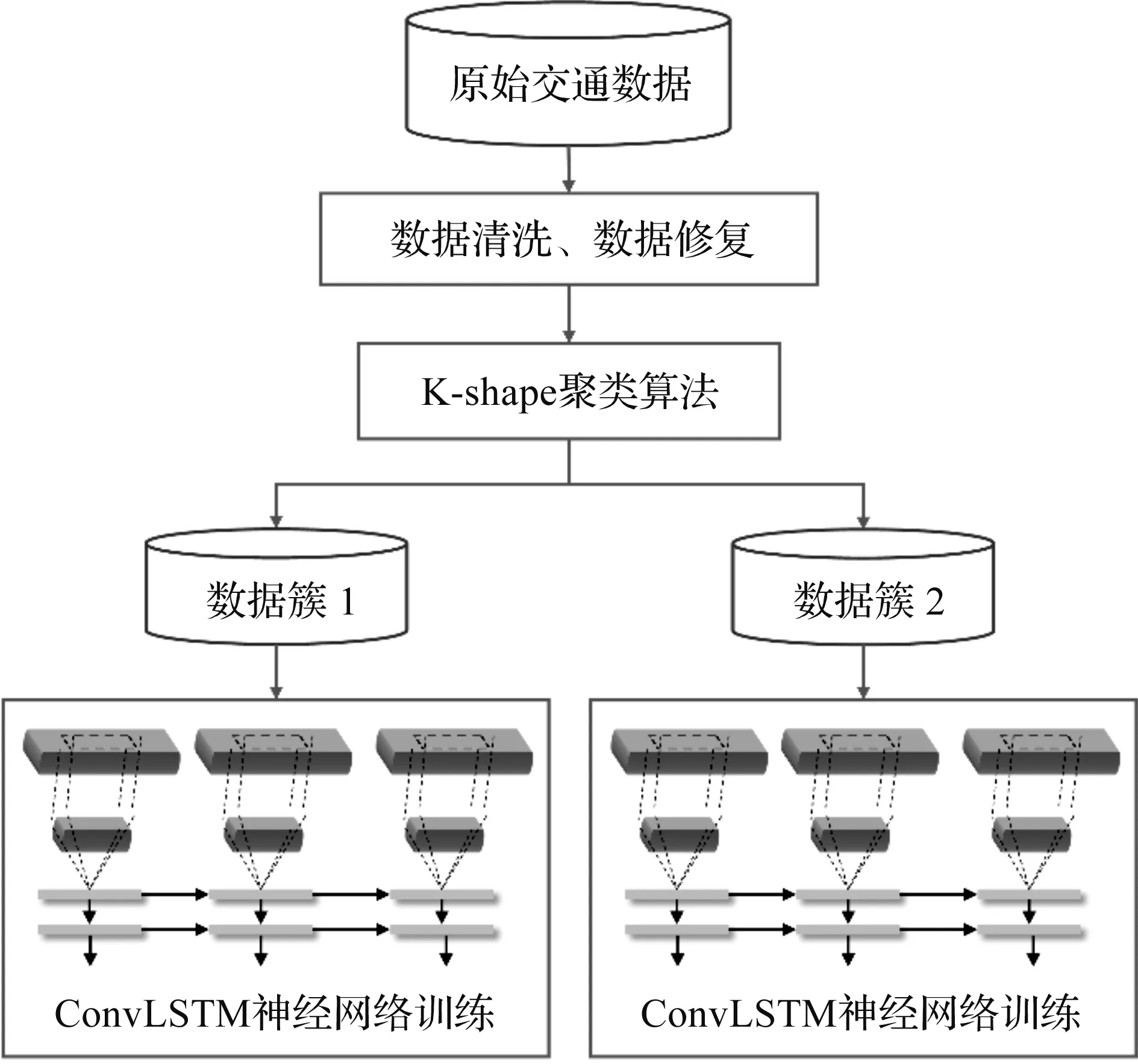
图1 预测模型架构Fig.1 Prediction model architecture
2 交通数据分析
2.1 数据采集及预处理
笔者选用的快速路交通流数据来自杭州交通管理平台。数据主要包含快速路主线车道级别的交通流量、占有率和速度数据,以及快速路上匝道入口的过车数据,主要采集自中河-上塘高架中的7个微波检测点位。微波数据为2018年5月1日—7月17日总计78 d,总量约3 400万条,中河-上塘高架部分微波点位的展示如图2所示。
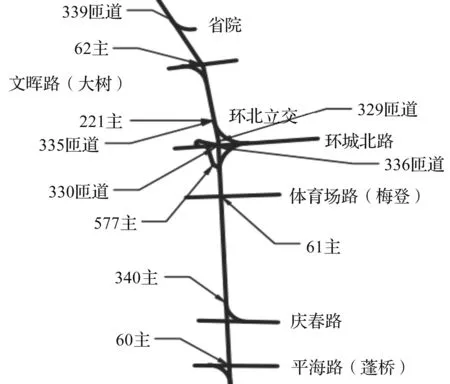
图2 快速路微波点位Fig.2 Microwave points on the expressway
在选择数据时,尽量避免选择包含大量缺失数据的路段或时间段,以免影响实验结果的准确性,然而大多数数据需要进行修复,并且需要对按照车道级别的微波数据进行处理。
一方面,按照路段名对该路段的交通流数据进行筛选,主要通过阈值方法剔除明显的异常数据,例如流量超过快速路运载能力的数值,或是速度远高于同时段平均水平的数值。在对异常数据进行处理之后,需要对缺失数据进行填充处理。一般将缺失数据分为短时缺失数据和长时缺失数据。短时缺失数据指在连续时间中缺失3个以下数据,对于这种情况,主要选取上一时刻的数据对缺失的数据进行填充。长时缺失数据指在连续时间内缺失3个及以上数据,一般是微波检测器的故障或者检修导致大片数据的缺失。对于长时缺失数据,利用交通流的时间相关性,对缺失数据进行处理,采用平均值法修补缺失的数据,修补公式为

(1)
式中:x(t)为需要补全的缺失数据;k为相邻数据总数。
另一方面,对完整数据进行车道级别的处理。首先将每个车道的流量数据相加得到主线流量数据;然后对每个车道的速度数据取平均得到主线的速度数据,最终得到实验数据。结构化后的交通数据样例时间为2018年6月1日,其结果如表1所示。

表1 结构化交通数据Table 1 Structured traffic data
时间序列数据是一组观测值,时间序列一般是相对于其他向量而言,包含时间关系的离散点的集合。一组交通流量时间序列数据是由环路检测器按照等间隔的时间戳收集的连续观测值。一组时间序列可以表示为Q=[q1,q2,…,qi,…,qn],其中qi为基于时间指数值的交通流量观测值。由于原始数据没有经过整理,需要对其进行过滤、修复和平滑处理。
经过数据清洗后,原始数据将成为串行数据。原始交通数据是指每条公路的检测点在某一时刻的交通信息。在数据采集之后进行数据清洗和数据修复工作,之后在使用局部加权回归(LOWESS)方法的基础上,对数据进行平滑处理。经过处理后的数据比原始数据更加平滑、连续,符合实际情况,有助于神经网络的训练,提高神经网络的预测性能。
2.2 数据分析
为了探索不同时间段的交通流特性,对快速路主线交通流特性进行研究。2018年6月1日星期五上塘—中河高架6个路段的流量立体图如图3所示。由图3可知:选择的路段方向是南北走向,即惠明路—大关路走向。流量呈现出较强的波动性,在4:00到达波谷,随后在4 h内逐渐增长到达峰值,并且持续较长时间维持较高的流量值,在20:00之后流量逐渐下降。流量的波动主要受到主线上游到达交通流和出入口匝道交通流的随机性影响。从地理位置来看:惠明路路段的交通流量最大,其后依次是凤起路和文晖路。而从惠明路—凤起路—环城北路路段的流量依次递减,出口匝道的流量随机性影响对于这些路段的冲击较大。
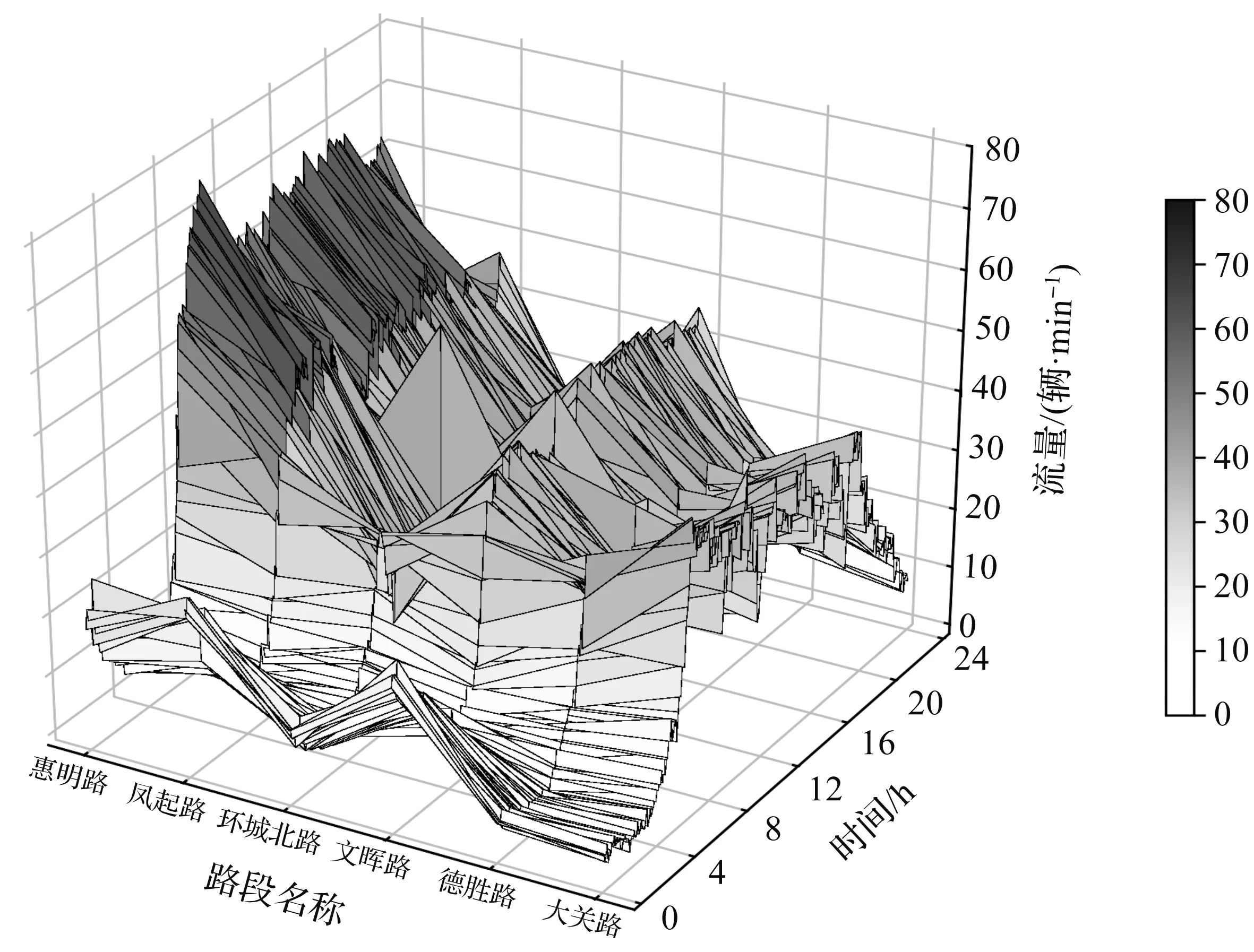
图3 工作日上塘—中河快速路各路段流量立体图Fig.3 Stereogram of different traffic flow of Shangtang-Zhonghe expressway in weekday
路段流量的波动幅度与节假日关联程度较大,2018年6月2日星期六上塘—中河高架6个路段的流量立体图如图4所示。由图4与图3的对比可知:快速路总体流量有较大幅度的减少,高峰时期从原来的8:00和18:00转变为16:00。在这个时间段,快速路承载着大部分通勤功能,在工作日的早高峰和晚高峰体现出较大的车流量,而节假日因为出行时间段的改变,快速路流量高峰时期也有所变化。

图4 周末上塘—中河快速路各路段流量立体图Fig.4 Stereogram of different traffic flow of Shangtang-Zhonghe expressway in weekend
3 基于时间聚类的交通流量预测模型
3.1 K-shape聚类算法
交通流量数据具有很强的时变性和周期性,许多研究者致力于开发各种各样的神经网络以提升交通流量预测的精度,然而由于交通环境的不同,将所有的数据输入到一个模型中可能会导致准确率较低。因此,不应该把所有的数据都输入到一个模型中,其原因有:1) 许多传感器的观测数据往往是高度相关和冗余的,一个包含许多不重要变量的模型通常预测能力较差,而且往往难以解释;2) 一些传感器之间可能不存在因果关系,在预测中考虑这样的传感器只会增加成本,而不会提高性能,最近的一些研究部分支持了这一猜想,并表明了当预测模型中考虑了足够多的传感器时,预测误差将达到一个饱和值;3) 预测模型的大小还受到其他一些因素的制约,包括通信带宽、中央处理单元(CPU)和内存的容量,以及算法的复杂性。一个包含所有数据的超额模型如果无法进行实时预测,就会变得毫无用处[15],因而需要选择具有较大相关性的交通流量时间序列数据作为输入。
笔者采用一种无监督的时间序列聚类方法K-shape对时序数据进行划分[16],使用K-shape进行时间序列的聚类主要包括分配(Assignment)和细化(Refinement)两个环节。在分配步骤中,算法比较每个时间序列与所有计算的质心,并将每个时间序列分配给最接近质心的簇。在细化步骤中,迭代更新集群中心以反映前一步中集群成员的变化。将历史交通流量数据按天进行划分,1 d的交通流量时间序列数据是由环路检测器按照等间隔时间戳收集的连续观察数值,可以用D=[d1,d2,…,di,…,dn]表示,其中:di为根据时间索引值i观测到的交通流量值;n为时间间隔数。所有天数的流量时间序列可以用矩阵Q=[D1,D2,…,Di,…,Dm]表示,其中:Di为其中某一天的流量时间序列;m为天数。
K-shape使用一种新的时间序列距离测度方法,基于形状的距离(SBD),并根据SBD计算类的质心,与其他方法相比,K-shape更适用于时间序列的聚类。使用系数归一化,不管数据归一化的情况如何,都会给出-1~1的值。系数归一化将交叉相关序列除以各个序列自相关的几何平均值。序列归一化后,检测互相关最大化的位置,得出距离度量。
使用K-shape进行聚类的算法伪代码如下:
输入:Q为一个m×n的交通流时间序列矩阵,包含m天,每天长度为n的时间序列;k为聚类数。
输出:C为一个k×n的矩阵,包含k个簇中心,长度为n;X为一个m×1的矩阵,包含了划分给k个簇的m条时间序列。
1)iter←0
2)X′←[ ]
3)whileX!=X′ and iter < threshold do
4)X′←X
5)fori←1 tokdo
6)Q′←[ ]
7)forj←1 tondo
8)ifX(j)=ithen
9)Q′←[Q′;Q(j)]
10)C(i)←ShapeExtraction(Q′,C(i))
11)fori←1 tomdo
12)distmin←∞
13)forj←1 tokdo
14)[dist,q′]←SBD(C(j),Q(i))
15)if dist< distminthen
16)distmin←dist
17)X(i)←j
18)iter←iter+1
通过互相关方法度量时间序列的相关性,对于时间序列X=(x1,x2,…,xn),以及Y=(y1,y2,…,yn),互相关方法保持Y静止,使X沿着Y滑动,对于X的每一次滑动s,计算其内积,具体表达式为
Xs=(x1,x2,…,xn)
(2)
(3)
对于所有可能的滑动s,计算内积CC(X,Y),作为2个时间序列X与Y之间的相似度,等式为
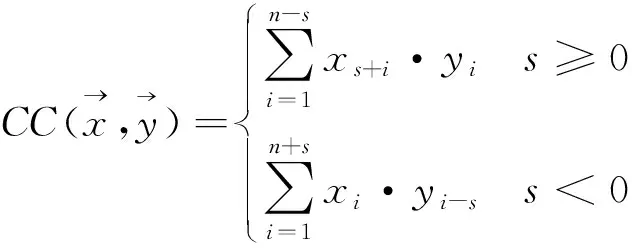
(4)
互相关是内积的最大值,表示在最佳相位滑动s条件下X与Y之间的相似度。因为在最佳的滑动条件下,模式相似的X与Y刚好对齐,两者的内积为最大,所以互相关方法克服了相位滑动问题,比较了2条时间序列的形状相似性。基于形状的距离SBD取值为[0, 2],其计算式为
(5)
式中s为1次滑动。
3.2 ConvLSTM交通流预测模块
交通流量通常与附近地点有较强的相关性。一条道路的未来交通状况可以通过其相邻道路的现状来预测。相邻2条道路之间的预测能力可以通过其时空相关性来估计,即在时间维度之外,可以考虑扩展空间维度提升交通流预测的准确性。笔者选用一种深度卷积神经网络预测交通流量,卷积长短时记忆神经网络(ConvLSTM)是深度学习预测模块的主要部分,最早由Shi等[17]提出用于解决时空序列问题,通过对全连接LSTM进行扩展,使状态之间的转换也具有卷积结构。ConvLSTM模块包含卷积神经网络和LSTM网络,卷积神经网络由2个卷积层组成,LSTM网络分别包含2个LSTM层。ConvLSTM使用一维卷积操作提取交通流的空间特征,使用LSTM提取时间维度的特征,以此预测交通流量[11]。ConvLSTM结构如图5所示,将多个一维卷积和LSTM层进行堆叠,以提升深度神经网络的预测效果。

图5 卷积LSTM神经网络结构Fig.5 Convolutional-LSTM neural network structure
ConvLSTM的输入如式(1)所示的时空交通流量,为了提取空间特征,在每个时间步长t对流量数据Fp×T进行一维卷积运算,一维卷积核滤波器通过滑动滤波器获取局部感知域。待预测点及其邻近地区的历史交通流量矩阵可以表示为
式中:p为检测的站点数;T为时间步长。
一维卷积核滤波器通过滑动滤波器获取局部感知域,卷积核滤波器的过程可以表示为
Y=σ(Ws*F+bs)
式中:Ws为滤波器权重矩阵;bs为偏置;Y为卷积层输出。
由于数据有限,模型中空间特征的维度不大,在卷积层之后不应用池化层。空间信息经过2个卷积层处理后,再将输出连接到LSTM网络。为了提高深度神经网络的性能,传统的方法是增加模型的层数,将多个LSTM层堆叠到模型中,以捕获更高层次的交通流特征,通过堆叠LSTM层,每个LSTM层都会接收上一层的隐藏状态作为输入。通过本地的输入和过去状态来确定网络中某个单元的未来状态,ConvLSTM的基本公式组为
it=σ(Wxi*Xt+Whi*Ht-1+Wci∘Ct-1+bi)
ft=σ(Wxf*Xt+Whf*Ht-1+Wcf∘Ct-1+bf)
Ct=f∘Ct-1+it∘tanh(Wxc*Xt+Whc*Ht-1+bc)
ot=σ(Wxo*Xt+Who*Ht-1+Wco∘Ct+bo)
Ht=ot∘tanh(Ct)
式中:σ为激活函数;o为哈达玛积(Hadamard product),即矩阵各元素之间的乘积;it为输入门;ft为遗忘门;Xt为t时刻LSTM的输入;Ct为当前节点的状态;Ht为LSTM层的输出。可以看出输出是由当前节点的状态Ct和当前时刻的输出ot决定的。
4 实 验
4.1 聚类结果
K-shape对交通流量序列时间聚类结果如图6所示。根据曲线的相似度进行聚类,由图6可知:在相同的簇中,流量曲线呈现相近的走势;在2个不同的簇中,流量时间序列呈现出不同的趋势。在6:00—7:00时,2个簇中的流量序列差距达到峰值,可能是由于工作日与周末早高峰时期车流量的不同,以及天气、事故和交通管制等外部因素共同导致的。在区分不同交通流量模式时,如果考虑事故、天气和交通管制等各种外部因素会导致变量过多,难以通过建模进行区分。而K-shape基于曲线的相似度进行聚类,综合考虑了由于外部因素导致的曲线变化,可提升后续交通流量预测的精度。

图6 时间聚类结果Fig.6 Time clustering results
4.2 交通流预测结果
使用TensorFlow和Keras框架搭建深度学习模型。选择128作为批尺寸大小,训练时期设置为150,所有的深度学习模型均采用RMSprop作为优化器。训练集使用了48 d的数据(占总天数的84.2%),测试集使用了剩余9 d的数据(15.8%)。最佳滞后时间可以使模型的预测误差最小化,采用的最大滞后时间为60 min。使用12个历史值来预测后一个值是比较合理的,较少的历史值会导致预测结果偏差较大。历史值越多导致计算时间越长,容易出现过拟合。除了滞后时间,还需选择深度神经网络模型的最佳参数。
在对比实验的设置中,实验对照组的选择方法有3种:
1) 栈式自编码机(SAEs)[7]:栈式自编码机是一种新型的基于深度学习的交通流量预测方法,该方法内在地考虑了空间和时间的相关性。采用堆栈式自动编码器模型来学习通用的交通流特征,并以贪婪的层级方式对其进行训练。
2) 长短时记忆神经网络(LSTM)[18]:LSTM是一种循环神经网络变体。LSTM通过加入记忆单元,克服网络层间梯度传播导致的爆炸或梯度消失问题,并通过遗忘门和选择门加强对历史信息的记忆。在训练阶段,它通过对历史数据的学习,获得权重、偏移量和输出等参数,可以帮助识别和记忆历史数据的特征。
3) 卷积长短时记忆神经网络(ConvLSTM)[11]:ConvLSTM模块由卷积神经网络和LSTM构建而成,其中利用卷积神经网络提取交通流的空间特征,然后与LSTM连接,得到交通流的短期时间特征。
实验中使用平均绝对误差(MAE)、根平均平方误差(RMSE)、平均绝对百分比误差(MAPE)和决定系数(R2)这几种评价指标对预测结果及进行全方位评价。MAPE为0%表示模型完美,而MAPE大于100%表示模型有缺陷。当预测值与真实值完全吻合时,RMSE等于0,表示模型完美。R2值若为0,说明模型拟合效果很差,如果为1,说明模型无错误。
评价指标计算式分别为

各方法的预测性能如表2所示。由表2可知:与其他方法相比,TC-ConvLSTM取得了更好的预测效果和预测精度。与SAEs和LSTM对比,TC-ConvLSTM的MAE分别提升了1.181,1.262辆/h;MAPE分别提升了2.244%,0.698%;RMSE分别提升了1.603,1.131辆/h。与其他深度学习方法相比,TC-ConvLSTM取得了更高的预测精度。而对于没有时间聚类的方法,聚类后的神经网络精度也有所提升。说明模型前使用时间聚类方法可以进一步降低预测误差。
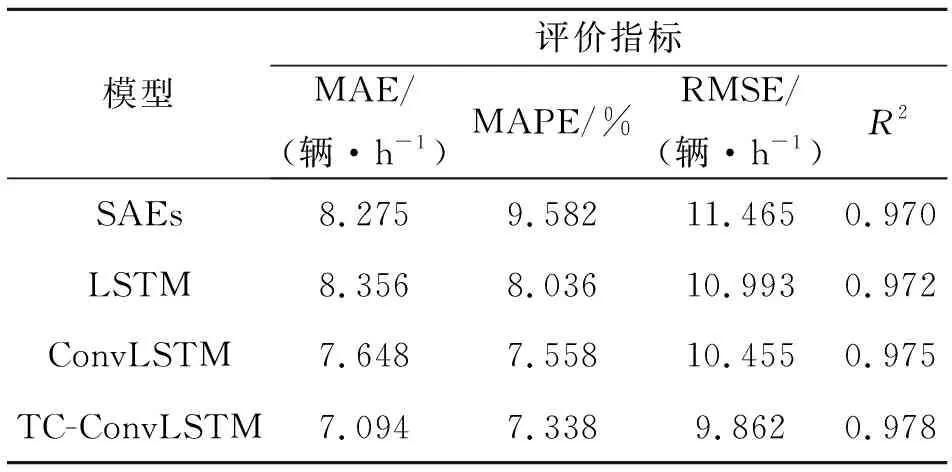
表2 交通流预测效果评价Table 2 Evaluation of traffic flow prediction
在5 min预测范围内,对0:00至24:00进行交通流量预测性能比较,其流量预测效果如图7所示。从图7可以看出:TC-ConvLSTM所取得的预测流量更加接近真实流量,尤其是在交通量波动较大的时段,并且在高峰和平峰时期都有较好的拟合度,而SAEs方法虽然在高峰时期精度较高,但是在平峰时期拟合度较差。与原先未添加聚类方法进行对比发现,时间聚类后模型预测精度更高,对于高峰时期的刻画更加准确。
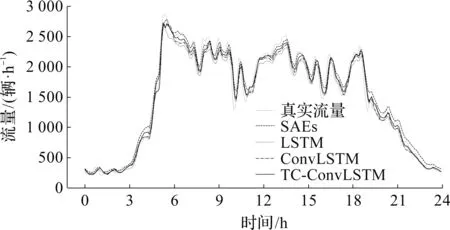
图7 流量预测效果Fig.7 Performance of traffic flow prediction
5 结 论
在交通流预测环节中,存在使用同一深度学习模型对所有的交通数据进行训练、预测的问题,忽略了交通流在不同的外部条件影响下呈现不同的趋势和波动特性的情况,以及交通流空间维度的关联性。针对以上问题,提出了一种基于时间序列聚类的深度神经网络交通流预测方法。笔者采集快速路的交通流数据,并对数据进行筛选、清洗和修复;使用K-shape方法对交通流数据进行聚类,K-shape是一种无监督学习的时间聚类算法,考虑时间序列的波动相似性,适用于对受到节假日、天气和事故等外部因素影响的不同交通模式进行划分;对聚类得到的不同簇分别使用卷积长短时记忆神经网络进行训练。实验结果表明:与其他深度学习方法相比,笔者方法预测的精度更高,而与未添加时间序列聚类的神经网络方法相比,笔者方法预测效果有较为明显的提升,体现了前期聚类的效果。
