基于Weibull分布的脆性岩石峰后应力-应变曲线特征及其统计损伤模拟方法

2022-07-14杨楚卿

自然灾害学报 2022年3期

张超，白允，杨楚卿，雷勇

（湖南科技大学岩土工程稳定控制与健康监测湖南省重点实验室，湖南湘潭 411201）

引言

岩石工程已广泛存在于公路、铁路、矿山和土木等领域，各类岩石工程（如地下结构与隧道、边坡、基础工程，等等）的变形分析与计算已成为其结构设计不可或缺的重要内容，而合理的岩石本构模型是保证岩石工程稳定性控制和安全预测的关键。一般而言，应力水平是决定岩石表现为脆性变形还是延性变形的关键因素之一［1－2］，当围压低于脆延转换临界值时，岩石内部微裂纹迅速扩展、相互贯通，应力达到峰值点（极限强度）以后不断发生跌落即应变软化，其破坏模式表现为脆性；当围压高于脆延转换临界值时，岩石内部微裂纹仍发生扩展并相互贯通，但应力达到极限强度以后不发生跌落即应变硬化。由于岩石脆性变形破坏无明显预兆，产生的危险性和破坏性极大，是岩石工程灾害频发的主要原因，因此，开展脆性岩石峰后应力-应变曲线特征及其统计损伤模拟方法研究对岩石工程结构灾害防治工作具有重要的理论价值。

岩石刚性伺服力学试验机研发成功以后，脆性岩石峰后应力-应变曲线得以实时测得，众多学者对脆性岩石峰后变形力学特性的研究有了快速进展。根据岩石三轴压缩试验规程，可获得不同围压作用下岩石全应力应变曲线，在此基础上对岩石峰后破坏特征进行分析，揭示了岩石受荷变形破裂全过程的基本规律，尤其是岩石峰后应力跌落过程是连续的，完全破坏以后仍具有残余承载能力［3］。三轴压缩条件下岩石变形破坏全过程模拟方法研究也在不断探索，由于岩石变形破坏伴随着内部微裂纹不断孕育、发展和相互贯通，当岩石发生损伤以后，岩石变形力学特性已超出弹性理论研究范畴，从连续介质力学角度分析岩石变形破裂的物理基础已发生改变［4－5］，而岩石材料内部存在的大量微裂隙或微孔隙正是损伤力学理论所研究的范畴［6－7］，于是，基于有效应力概念和应变等效假设，将统计强度理论和连续损伤理论相结合，提出了统计损伤的概念，从而建立了脆性岩石统计损伤本构模型，其研究内容主要集中在岩石几何损伤模型的构建方法［8］、岩石破坏准则和微元体强度随机分布类型［9］、岩石发生损伤存在阈值的影响［10］以及本构模型参数的确定方法［11］等方面，从而不断地完善岩石统计损伤软化本构模型理论，使该类模型尽可能地能够模拟脆性岩石变形破坏全过程。然而，目前该类模型理论曲线在描述岩石峰后应变软化行为具有强烈的随机性，即无法定量地模拟脆性岩石峰后应力-应变试验曲线，这就导致难以利用该类模型预测脆性岩石达到极限强度以后的连续变形过程，但为文中开展脆性岩石峰后应力-应变曲线特征及其统计损伤模拟方法研究提供了一条可借鉴的途径。

为此，本研究针对已有岩石统计损伤软化本构模型在反映脆性岩石峰后应变软化行为方面存在的缺陷，以微元体强度服从Weibull分布为前提，探讨其分布参数对脆性岩石损伤演化规律产生的影响，提出一种新型几何损伤模型，然后结合统计损伤的概念，建立能够定量地模拟脆性岩石峰后应力-应变试验曲线的统计损伤软化本构模型，给出相应模型参数的确定方法，以期解决已有脆性岩石本构模型峰后理论曲线存在的强烈随机性，进一步完善岩石统计损伤本构模型的研究内容与方法，为各类岩石工程结构变形与分析计算提供有力的本构模型理论依据，从而更好地进行岩石工程稳定性控制和安全预测。

1 脆性岩石统计损伤本构模型理论及分析

目前，Lemaitre提出的岩石损伤本构基本关系式［6］在岩石损伤力学理论中具有代表性，也得到了广泛应用，即

式中：σ和ε分别为名义应力张量和名义应变张量；C和D为岩石材料的弹性矩阵和损伤变量。

岩石材料作为一种天然地质材料，其内部构造不均质从而使岩石各微元体强度数值不尽相同，因此，基于统计强度理论假定各微元体强度F服从Weibull分布［7］，即

式中：m和F0为微元体强度的分布参数。根据岩石三轴压缩试验，当岩石轴向承受较低荷载时，岩石内部少量的、低强度的微元体发生破坏，阴影面积较小，如图1（a）所示，随着轴向荷载不断增大，微元体发生破坏的数目不断增多，阴影面积不断增大，如图1（b）所示，当岩石所受应力超过极限强度以后，大量微元体开始迅速发生破坏，岩石峰后应力快速跌落，表现为应变软化，但仍有少量的、强度极大的微元体不能发生破坏，由此岩石进入残余强度变形阶段，但仍具有残余承载能力。由此可见，阴影面积的变化可用于描述岩石变形破坏过程中微元体破坏累积过程，则阴影面积可用于定义损伤变量D，即

图1 微元体强度F概率密度函数Fig.1 Probability density function of microelement strength F

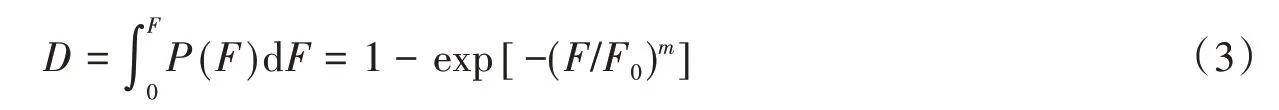
将式（3）代入式（1）可得岩石统计损伤软化本构模型，即

由此可知，要使该模型能够模拟岩石变形破裂全过程，需对模型参数进行确定。该模型参数包括岩石材料弹性矩阵C，度量微元体强度F的相关参数以及分布参数m和F0，前两类参数可由岩石基本力学试验获得，参数物理意义明确，属于试验类定常数，因此关键在于分布参数m和F0的确定方法。

目前，分布参数m和F0的确定方法主要有线性拟合法［12］、优化反分析法［13］和峰值点法［14］等。线性拟合法首先将本构模型方程变换为关于待拟合参数的线性方程，然后利用岩石三轴压缩试验曲线进行线性拟合从而获得特定围压作用下分布参数m和F0的数值，该方法参数获取便捷，但不具有物理意义，而且不同围压对岩石损伤本构模型产生不同的影响，导致特定围压下分布参数值对其余围压下岩石应力-应变曲线的适用性较差。优化反分析法是将不同围压作为不同工况并建立目标函数以及根据经验确定的参数变化范围，构成一个有约束的非线性规划问题，利用单纯形法求解分布参数，但需要基于大量的试验数据且获得的参数解并不唯一。峰值点法要求本构模型方程需同时满足如下条件：

式中：σ1c和ε1c分别为脆性岩石所受应力达到极限强度时的最大主应力及相应的主应变。由此可见，只需本构模型理论曲线经过试验峰值点且具有相应的极值特性即联立上述方程从而求解分布参数m和F0，该方法处理简捷，物理意义明确，得到了广泛应用。于是，根据上述参数确定方法即可获得岩石统计损伤软化本构模型理论曲线［11］，如图2所示，该类模型能够较好地反映岩石峰前变形特征和应变软化特征，但无法反映残余强度变形特征。于是，曹文贵等［15］认为岩石发生损伤破坏后仍具有残余强度，从而建立了新型岩石损伤模型，在基础上引入统计损伤的概念，建立了考虑岩石统计损伤软化本构模型，使该类模型还能够反映岩石残余强度变形特征。然而，上述研究都不能定量地描述脆性岩石峰后应力跌落过程，模型理论峰后曲线与试验峰后曲线存在较大偏离现象，究其原因在于2方面：一方面是统计损伤本构模型理论本身存在问题，该问题非常复杂，这里暂不讨论；另一方面是认为本构模型理论正确的前提下，其模型参数确定方法存在的缺陷所造成的，这是建立本构模型的重要组成部分，现对此进行分析。

图2 统计损伤软化本构模型理论曲线Fig.2 Curves of statistical damage softening constitutive model

如上所述，脆性岩石统计损伤软化本构模型参数［16－17］可分两类：一类为岩石材料弹性矩阵C（如弹性模量E、泊松比μ、内摩擦角φ和黏聚力c）和度量微元体强度F的相关参数（如M-C强度准则α和κ），其数值主要取决于岩石物理性质，属于基本力学参数，它们不会因本构模型或模型理论的改变而发生变化，因此，该类模型参数并非导致模型理论峰后曲线与试验峰后曲线存在较大偏离的原因；另一类为微元体强度服从Weibull分布的参数m和F0，广泛采用峰值点法进行确定，但峰值点法仅仅要求模型理论曲线需经过试验曲线峰值点且满足极值特性，由此获得的2个方程无法对脆性岩石峰后应力-应变曲线特征产生任何约束或控制，致使模型理论峰后曲线存在强烈的随机性，无法定量地模拟岩石峰后应力跌落过程，同时由该方程组获得的分布参数m和F0数值具有唯一性，仅适用于模拟特定围压作用下脆性岩石应力-应变试验曲线。

因此，将在探讨分布参数m和F0对脆性岩石损伤演化规律产生的影响基础上，提出一种新型脆性岩石损伤模型，然后结合统计损伤的概念，建立能够定量地模拟脆性岩石峰后应力-应变试验曲线的统计损伤软化本构模型。

2 新型脆性岩石损伤模型

由前述分析可知，脆性岩石统计损伤软化本构模型理论曲线的变化规律除受岩石材料基本力学参数的影响以外，还受损伤变量D变化的影响，但是岩石材料基本力学参数属于试验类定常数，而损伤变量D的变化规律主要与分布参数m和F0密切相关，因此，分布参数m和F0对模型理论曲线的变化规律产生重要影响，故基于式（3）探讨分布参数m和F0对损伤变量D产生的影响，如图3所示，可得：

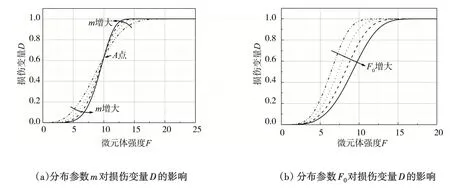
图3 分布参数m和F0对损伤变量D的影响Fig.3 Effects of distribution parameters m and F0 on damage variable D

（1）随着微元体强度F的增大，损伤变量D不断增大且曲线形状表现为“S型”，损伤变量D的数值变化区间为[0，1]。

（2）分布参数F0保持不变，随着分布参数m的增大，损伤变化率（∂D/∂F）不断增大，D-F曲线形状保持为“S型”并绕着定点A作逆时针转动。根据岩石损伤本构基本关系式即式（1）可知，损伤变化率增大使（1-D）的数值快速降低，岩石峰后应力跌落加快，其破坏模式表现为脆性程度增大。

（3）分布参数m保持不变，随着分布参数F0的增大，损伤变化率（∂D/∂F）不断减小，D-F曲线形状保持为“S型”且趋于向微元体强度F增大方向移动。根据岩石损伤本构基本关系式即式（1）可知，损伤变化率减小使（1-D）的数值慢速降低，岩石峰后应力跌落减慢，其破坏模式表现为脆性程度减小。

由此可见，分布参数m和F0对损伤变量D的变化规律产生重要影响，进而影响岩石峰后应力跌落即峰后应力-应变曲线特征，然而根据特定围压作用下岩石三轴压缩试验数据，由峰值点法确定的分布参数m和F0数值具有唯一性，使现有岩石统计损伤软化本构模型针对特定围压情况仅能够产生一条理论曲线，而且此条理论曲线由于峰值点法的原因而峰后表现出强烈的随机性，无法定量地模拟岩石峰后应力跌落过程。然而，峰值点法处理简捷，参数物理意义明确即分布参数m为岩石材料的均匀系数，分布参数F0为微元体强度统计均值，因此，本研究在继承该方法优越性的前提下，经过不断地尝试和验证，拟引入参数λ和η，提出新型脆性岩石损伤模型，即

式中：σi、σ′i和σr分别为脆性岩石表观应力、有效应力和残余应力。在分布参数m和F0数值保持唯一性的情况下，参数λ和η能否使在此基础上建立的统计损伤软化本构模型定量地模拟出脆性岩石峰后应力跌落过程，将在第4节进行分析和验证。

3 脆性岩石变形破裂过程统计损伤模拟方法

根据损伤力学理论可知，脆性岩石可抽象为由损伤部分和未损伤部分组成，而未损伤部分的变形力学特性服从广义虎克定律［18］，即

式中：E和μ分别为脆性岩石弹性模量和泊松比；σ′i、σ′j和σ′k分别为未损伤部分在i、j和k方向的有效应力；εi为脆性岩石在i方向的应变。由于三轴压缩试验条件下岩石试件在轴向荷载压缩方向发生破裂变形并逐渐丧失承载能力，围压约束岩石试件发生侧向变形并起到提高轴向承载能力的作用，因此可近似认为岩石试件损伤主要发生在轴向，忽略侧向围压方向发生的损伤。于是，式（8）可改写为

于是，将式（9）代入式（7）可得

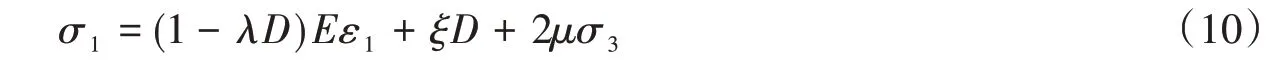
其中，

由于脆性岩石变形破裂行为的本质是微元体发生破坏的数目不断增多的过程，因此，本文在考虑脆性岩石力学特性受应力状态的影响基础上，将M-C强度准则［17］作为判断微元体是否发生破坏的依据，即

其中，

式中：φy和cy分别为脆性岩石所受应力达到损伤阈值时的内摩擦角与黏聚力。根据损伤变量D变化规律可知，当脆性岩石仅发生弹性变形时，微元体未发生破坏，损伤变量D等于0；当脆性岩石发生损伤变形时，微元体开始发生破坏且破坏数目不断增多，损伤变量D不断增大；当脆性岩石变形持续增大而应力不再增加时，微元体破坏数目已达上限，损伤变量D等于1/λ并保持不变。于是，新型脆性岩石损伤模型下损伤变量D可表述为

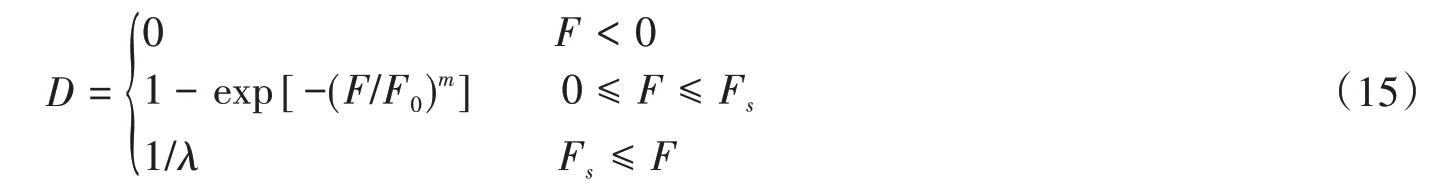
式中：Fs为损伤变量D恰好达到1/λ时的微元体强度值。由于脆性岩石损伤演化过程是连续的，由式（15）可确定出Fs，即

于是，将式（15）代入式（10）可得脆性岩石变形破裂过程统计损伤模拟方法，即

要使式（17）能够模拟出脆性岩石变形破裂过程，还需给出分布参数m和F0以及参数λ和η的确定方法。于是，本研究考虑峰值点法的优越性并继承其参数确定方法，可得分布参数m和F0的解析表达式，即

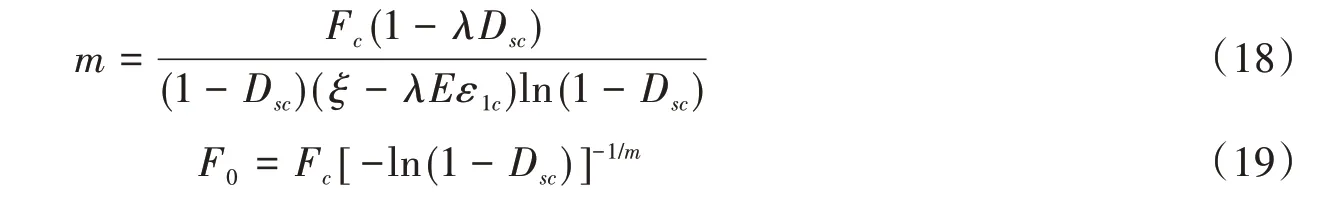
其中，

由于参数λ和η变化对脆性岩石损伤演化规律及其损伤本构模型理论曲线产生的影响未知，因此暂无法给出其确定方法，需参数分析之后给出相应表达。值得注意的是，现有脆性岩石统计损伤软化本构模型是最大主应力σ1和最大主应变ε1之间的理论曲线，而三轴压缩条件下脆性岩石实测曲线是轴向应力σ1t和轴向应变ε1t之间的试验曲线，两者曲线之间存在明显差异，需给出它们之间的理论关系，即

式中，εc为静水压力下岩石产生的初始应变，其数值为（1-2μ）σ3/E。于是，将式（22）和式（23）代入式（17）可得脆性岩石修正统计损伤软化本构模型。

4 参数（λ和η）分析及本构模型验证

YUMLU.M等［19］基于三轴压缩试验机给出了围压分别为3，5和8 MPa作用下砂岩轴向应力与轴向应变试验曲线，如图4所示，砂岩弹性模量E=27.0 GPa，泊松比μ=0.25，内摩擦角φy=50°，黏聚力cy=13.17 MPa。为了清楚地表明已有脆性岩石统计损伤软化本构模型理论曲线存在的缺陷以及采用本文模型和方法所带来的优越性，首先将参数λ和η均赋数值为1，本文模型则转化为已有脆性岩石损伤本构模型［15］，将其模型理论曲线与试验曲线进行比较，然后再对参数λ和η进行分析，讨论其影响并给出其确定方法，最后对本文模型和方法的可行性与合理性进行验证。

4.1 不考虑参数λ和η影响的脆性岩石统计损伤软化本构模型分析

为了不考虑参数λ和η的影响，将参数λ和η均赋数值为1，则本文模型转化为已有脆性岩石损伤本构模型［15］，根据已有方法可得其模型理论曲线σ1－ε1、修正模型理论曲线σ1t－ε1t以及砂岩损伤演化曲线D－ε1t，并将已有理论曲线与砂岩试验数据进行比较，如图4所示，可以看出：

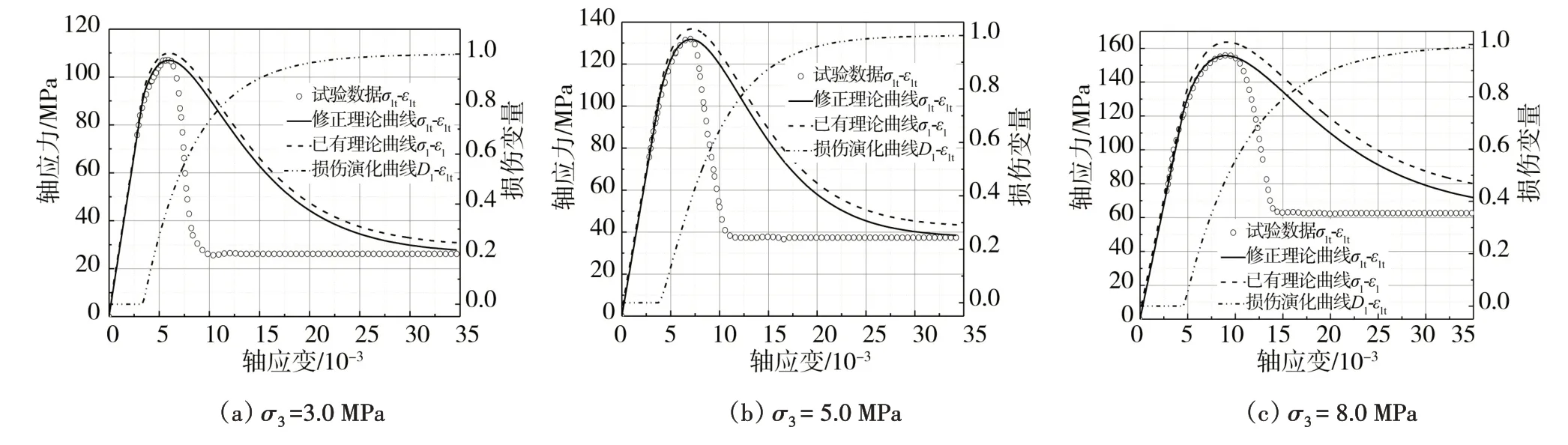
图4 已有模型理论曲线［15］（λ=η=1）与砂岩试验数据对比Fig.4 Comparison of experimental data of sandstone and theoretical curves of existing model［15］（λ=η=1）

（1）已有模型理论曲线σ1－ε1能够定性地反映砂岩线弹性、屈服硬化、应变软化和残余强度等4个变形阶段，但存在明显缺陷，对于峰值强度之前，随着围压的增大，已有模型理论曲线与砂岩试验数据的偏离程度不断增大，对于峰值强度之后，已有模型理论曲线明显偏离砂岩试验数据，且与围压水平无关。

（2）修正模型理论曲线σ1t－ε1t能够定量地描述砂岩峰值强度之前的试验曲线，尽管峰值强度之后的修正模型理论曲线与砂岩试验曲线的偏离程度减小，但两者之间的差距仍然不可忽略或近似。

（3）砂岩损伤演化曲线D－ε1t形状基本表现为“S型”，当砂岩未发生损伤即处于弹性变形阶段时，损伤变量D为0，当砂岩进入屈服硬化和应变软化阶段时，损伤变量D由0逐渐增大，直至砂岩进入残余强度变形阶段，损伤变量D等于1并保持不变，可见D－ε1t能够对砂岩阶段性变形特征进行合理阐释。

由此可见，不考虑参数λ和η影响的脆性岩石统计损伤软化本构模型及其修正模型存在明显缺陷，它们均无法很好地模拟脆性岩石峰后应力跌落过程，因此为了解决该问题，文中提出了新型脆性岩石损伤模型即式（7），进而在此基础上建立了脆性岩石修正统计损伤软化本构模型。

4.2 参数λ和η分析

为了探讨参数λ和η的影响并给出其确定方法，文中采用控制单参数变量方式即将参数λ和η分别赋数值为1，考虑单参数的变化对脆性岩石损伤演化规律及其损伤本构模型理论曲线产生何种影响，分别如图5和图6所示。

图5 参数λ对模型理论曲线和损伤演化规律的影响（η=1）Fig.5 Effects of parameterλon theoretical curves and damage evolution law（η=1）

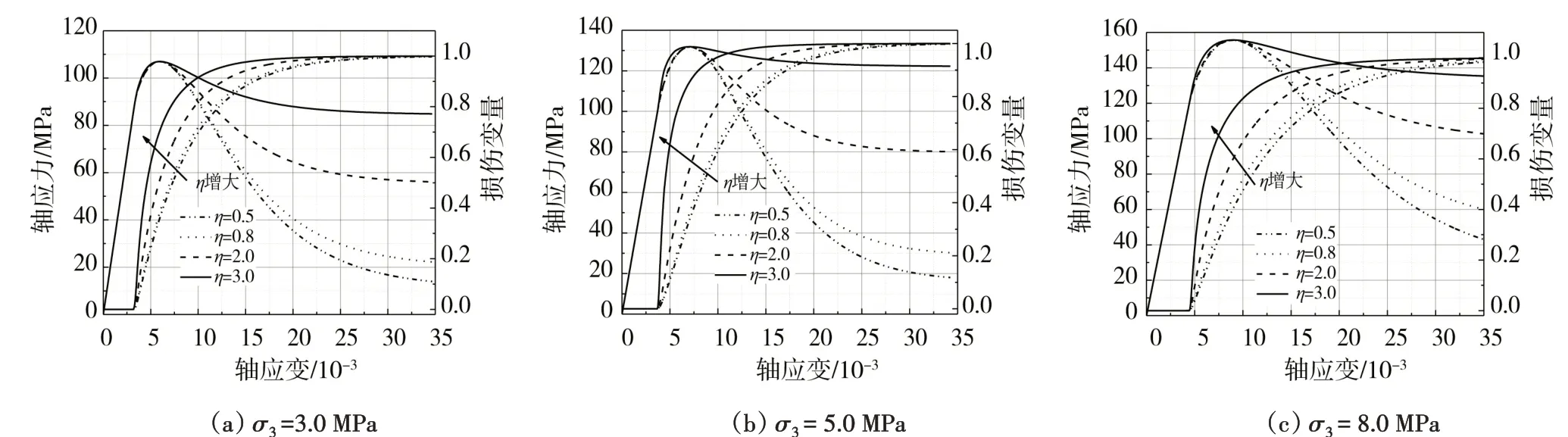
图6 参数η对模型理论曲线和损伤演化规律的影响（λ=1）Fig.6 Effects of parameterηon theoretical curves and damage evolution law（λ=1）

（1）不同围压作用下峰值强度之前模型理论曲线不受参数λ和η变化的影响，继承了已有修正理论模型（λ=η=1）的优点，能够很好地反映砂岩线弹性变形阶段和屈服硬化变形阶段，不同围压作用下峰值强度之后模型理论曲线受参数λ和η变化影响显著。

（2）控制参数η不变（赋参数η数值为1），随着参数λ的增大，峰值强度之后的模型理论曲线应力跌落过程加快，残余应力降低，损伤变化率增大，损伤演化理论曲线形状基本保持为“S型”并绕固定点A作逆时针转动，从而表明参数λ与Weibull分布参数m对损伤演化规律产生的影响一致。

（3）控制参数λ不变（赋参数λ数值为1），随着参数η的增大，峰值强度之后的模型理论曲线应力跌落过程减慢，残余应力增大，损伤变化率增大，损伤演化理论曲线形状基本保持为“S型”并趋于向轴应变减小方向移动，从而表明参数η与Weibull分布参数F0对损伤演化规律产生的影响接近相同。

由此可见，参数λ和η对损伤演化理论曲线的影响与Weibull分布参数m和F0对损伤演化理论曲线的影响是等效的，这表明基于峰值点法确定的Weibull分布参数m和F0数值在保持不变的情况下，通过改变参数λ和η的数值来影响损伤演化理论曲线变化规律，进而使统计损伤软化本构模型能够模拟脆性岩石峰值强度之后的应力跌落过程，这一研究思路是可行的。

根据参数λ和η分析可知，参数λ和η的变化对不同围压作用下峰值强度之前模型理论曲线不产生影响，但对峰值强度之后模型理论曲线变形特征起着关键作用。由于岩石峰值后区变形特征可由脆性指标和残余应力进行表征，因此可提出参数λ和η的确定方法如下：

张超等［20］综合考虑全应力应变曲线峰前峰后对岩石脆性程度的共同影响，提出岩石的新脆性指标B L，可表示为

其中，

式中：ε1r为岩石所受应力为残余应力时的应变。B L数值越大，代表岩石脆性程度越高，由式（24）～式（25）可得ε1r的表达式，即

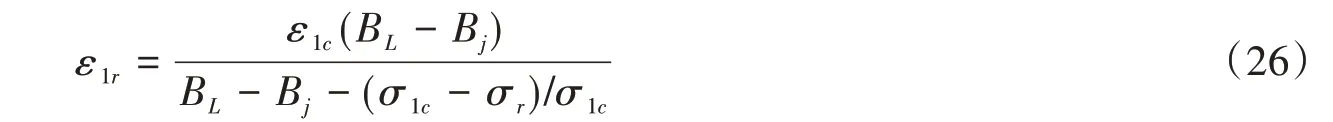
将式（26）代入式（12）可得岩石所受应力恰好达到残余应力σr时的Fs，即

于是，将式（27）代入式（15）可得微元体强度达到Fs时的岩石损伤变量Ds，即

根据连续性损伤条件，由式（15）可得参数λ的确定方法，即

根据岩石残余强度变形阶段特征可得

于是，将式（17）第3式代入式（30）可得参数η和参数λ的数值相等。

4.3 考虑参数λ和η影响的脆性岩石修正统计损伤软化本构模型验证

根据上述参数的确定方法可得出文中理论模型相关参数，如表1所示，将其代入考虑参数λ和η影响的脆性岩石修正统计损伤软化本构模型，可得不同围压下砂岩变形破坏全过程理论曲线，并将其与砂岩试验数据进行比较，如图7所示。

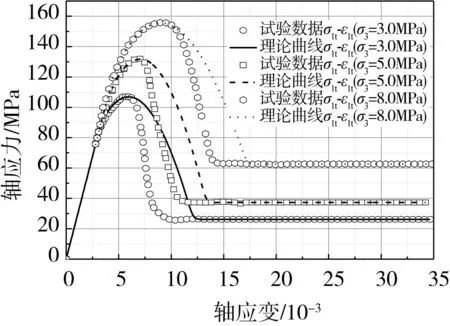
图7 本文修正理论模型曲线与砂岩试验数据对比Fig.7 Comparison of experimental data of sandstone and theoretical curves of proposed model

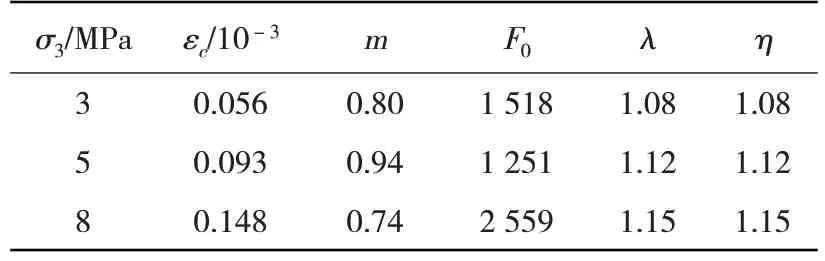
表1 理论模型相关参数Table 1 Related parameters of theoretical model

由此可见，本研究修正理论模型能够准确地描述砂岩峰值强度之前线弹性和屈服硬化等变形阶段，继承了已有修正理论模型（λ=η=1）的优点，也能够较好地模拟出砂岩峰值强度之后试验曲线即应变软化和残余强度变形阶段，尽管理论曲线应变软化阶段与砂岩试验数据尚存些许偏离，究其原因，本文模型和方法不适用于脆性指标趋于极大的极端情况，也未考虑砂岩初始损伤所带来的影响，但它明显缩小砂岩峰值强度之后应力跌落过程与试验数据的偏离程度，表明本文模型和方法具有一定的合理性与可行性。