基于黏度时变性的Herschel-Bulkley流体劈裂注浆扩散特性研究

2022-07-14刘海明卢昊正王忠伟丁文云

自然灾害学报 2022年3期

刘海明，卢昊正，南敢，王忠伟，梁瑞，丁文云

（1.昆明理工大学建筑工程学院，云南昆明 650500；2.保（山）施（甸）高速公路投资开发责任公司，云南保山 678200；3.中铁二院昆明勘察设计研究院有限责任公司，云南昆明 650500）

引言

在公路、边坡、隧道等工程施工中，滑坡、崩塌、泥石流等自然地质灾害时有发生，不仅导致工期延误和经济损失，甚至会造成人员伤亡。注浆是指用一定的压力将浆液通过导管注入到土体中，通过填充裂缝和孔隙［1］、排挤水分和气体，硬化后胶结土体，从而改善土的性质以达到防渗和加固的效果，因此注浆技术已成为自然地质灾害防治的有效手段之一。劈裂注浆应用广泛，但机理较为复杂，目前针对这方面的研究相对较少，其理论远远滞后于工程建设，影响了注浆技术在工程地质灾害防治领域的应用。

浆液在土体中的扩散很大程度上决定了注浆加固的效果［2］，另一方面，注浆扩散过程可能会对地下水环境造成污染［3］。秦鹏飞［4］利用PFC2D模拟浆液的扩散过程，从细观的角度揭示了浆液改变地层孔隙率的机理，探究了浆液黏结强度的影响。张玉等［5］通过注浆参数的正交试验，总结出浆液在不同参数及水平影响下的扩散规律，阐述了浆液渗透与流动的关系。欧阳进武等［6］针对宾汉流体的劈裂注浆问题，推导出浆液扩散方程，并研究了浆液在地基土中的流动。魏建平等［7］建立了考虑浆液自重的隧道注浆模型，证明了注浆改良断层围岩的可行性。Zhou等［8］开展了大压力、注浆试验，研究高注浆速度对孔隙率的影响。Sun等［9］基于粒子流理论，模拟了土体中的裂隙注浆的过程，分析了不同注浆参数时浆液的流动特性。Li等［10］建立了适用于隧道和地下软弱围岩的劈裂注浆计算模型，该模型考虑了时变性的影响，可求得裂隙宽度和注浆压力的经验解。杨秀竹［11］等推导出幂律型浆液在岩体中浆液扩散半径计算公式。阮文军［12］建立了稳定性浆液注浆扩散模型，其理论计算结果与工程实际相符。在岩土及其他领域，学者们对Herschel-Bulkley流体的流动规律进行了研究。李靖祺等［13］采用Herschel-Bulkley模型研究自密实混凝土的流动性能，Khamehchi等［14］通过实验证明该模型能更准确地描述微泡钻井液的流动过程，张广等［15］采用上述模型研究磁流变胶的流动特性。国外也有学者化学、生物及其他领域将Herschel-Bulkley模型用于研究流体的流变特性［16－17］。

综上所述，注浆理论对注浆参数的确定起指导性作用［18～19］，目前Herschel-Bulkley流变模型在注浆领域的研究较少，亟待完善有关理论。文中基于Herschel-Bulkley流变模型，假定浆液平板窄缝流动，考虑黏度的时变性，推导了劈裂注浆扩散半径理论公式，分析了注浆参数对浆液扩散半径的影响；并与不同流变模型计算结果及工程实例进行对比，以完善劈裂注浆理论的发展，从而为劈裂注浆技术在实际工程地质灾害防治的应用提供一定的指导作用。

1 劈裂注浆扩散公式推导

1.1 注浆基本假定

针对劈裂注浆扩散过程，基本假定如下所示：

（1）浆液为Herschel-Bulkley流体；

（2）裂缝中浆液的流动为层流；

（3）浆液流动过程中速度恒定；

（4）浆液黏度随时间变化；

（5）视浆液的运动路径为平板窄缝型，且其高度与宽度均匀，即δ(x)=δ,b(x)=b；（6）受注土层各向同性。

1.2 Herschel-Bulkley模型方程

Herschel-Bulkley模型与屈服应力相关，应用于土体劈裂注浆时，其本构方程为：

式中：τ0为屈服应力；K为稠度系数；γ为剪切速率；n为流变指数；τ为剪切应力。

Herschel-Bulkley模型对于几类常用流体都具有良好的适用性，其表达式如表1所示。

表1 不同流体模型参照表Table 1 Reference table for different fluid models

考虑时变性，对于浆液的剪切速率，有如下关系：

式中：υ为流动速度；y为中心高度。

黏度的改变直接影响注浆，在注浆过程中，浆液的黏度随时间逐渐增加。根据已有的研究［20］，考虑时间的影响，得浆液黏度的公式如式（3）所示。而流变指数可取n()

t≈n，因为时间对其影响不明显。

式中：K(t)为t时刻的稠度系数；C0为初始稠度系数；w为时变系数。

根据已有的研究［21］，初始稠度系数取值范围为10～70内，时变系数取值范围为9×10－3～33×10－3。

由式（1）计算可得K(t)，再代入式（3），可得式（4）

1.3 注浆公式推导

平板窄缝浆体力学分析模型如图1所示。

图1 平板窄缝模型Fig.1 Flat slit model

由流体动力与阻力平衡的条件，得如下方程（5）和（6）：

式中：Δp为浆液压力差；b为土体裂隙宽度；L为土体裂隙长度；δ为土体裂隙高度；τ为剪应力；τe为剪切应力。

计算式（5）和式（6），转化形式得：

联立式（1）与式（2）得：

将式（3）代入式（9）得：

式中：C为常数。

将式（11）代入式（10）得：

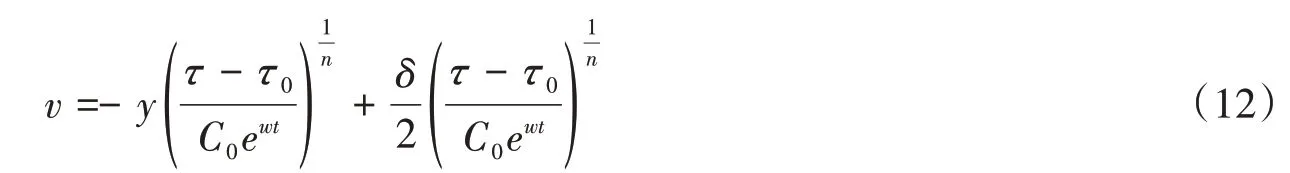
为方便后续公式推导与计算，将式（12）转换为积分形式，转换如下：

联立式（7）与式（8）得：

将式（14）代入式（13）并变换积分变量得：

由式（15）得：

将式（7）与式（8）代入上式得：

通过平板宽度b和平板缝隙厚度δ的单位时间流量q为：

将式（17）代入上式得：

2 浆液扩散特性分析

基于推导的劈裂注浆公式，对影响浆液扩散半径的各参数展开分析。参数基本取值如表2所示。

表2 参数基本取值表Table 2 Parameter basic value table

2.1 注浆压力差

（1）注浆压力差与初始稠度系数的关系

基于Herschel-Bulkley流体，针对注浆压力差ΔP的改变，取不同流变指数n，其他参数取值如表2，研究初始稠度系数C0的影响。根据式（19）进行计算，注浆压力差ΔP值如图2所示。

分析图2结果发现，在其他参数相同的条件下，当初始稠度系数C0提高，注浆压力差ΔP也增大；流变指数n减小时，注浆压力差ΔP也减小；二者呈正相关。实际注浆中，水灰比越大，为达到同等注浆半径，所需注浆压力越小，公式结果与实际相符。

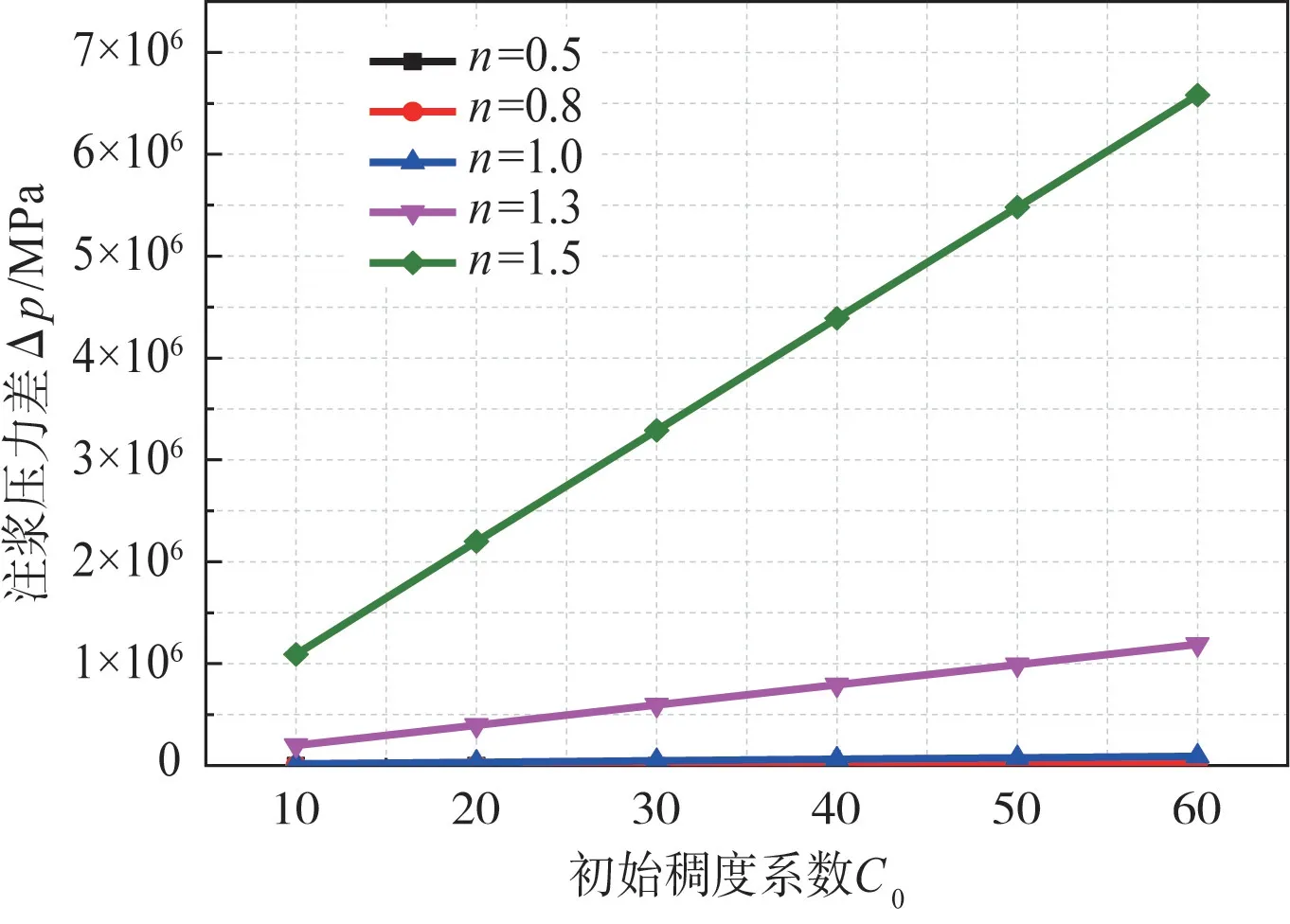
图2 初始稠度系数对注浆压力差的影响Fig.2 The influence of initial consistency coefficient

（2）注浆压力差与浆体时变系数的关系

基于Herschel-Bulkley流体，针对注浆压力差ΔP的改变，取不同流变指数n，其他参数取值如表2，研究时变系数w的影响。根据式（22）进行计算，注浆压力差ΔP值如图3所示。

分析图3结果发现，在其他参数相同的条件下，当流变指数n小于1.0时，时变系数w的改变，对注浆压力差ΔP几乎无影响。当n=1.3、1.5时，当w由0.010增大到0.025时，所需的ΔP开始增大；当w由0.025增大到0.030时，此时ΔP的增大幅度迅速提高，时变系数w的影响显著。

图3 浆体时变系数对注浆压力差的影响Fig.3 The influence of the time-varying coefficient of slurry on the grouting pressure difference

（3）注浆压力差与裂隙高度的关系

基于Herschel-Bulkley流体，针对注浆压力差ΔP的改变，取不同流变指数n，其他参数取值如表2，研究裂隙高度δ的影响。根据式（19）进行计算，注浆压力差ΔP值如图4所示。

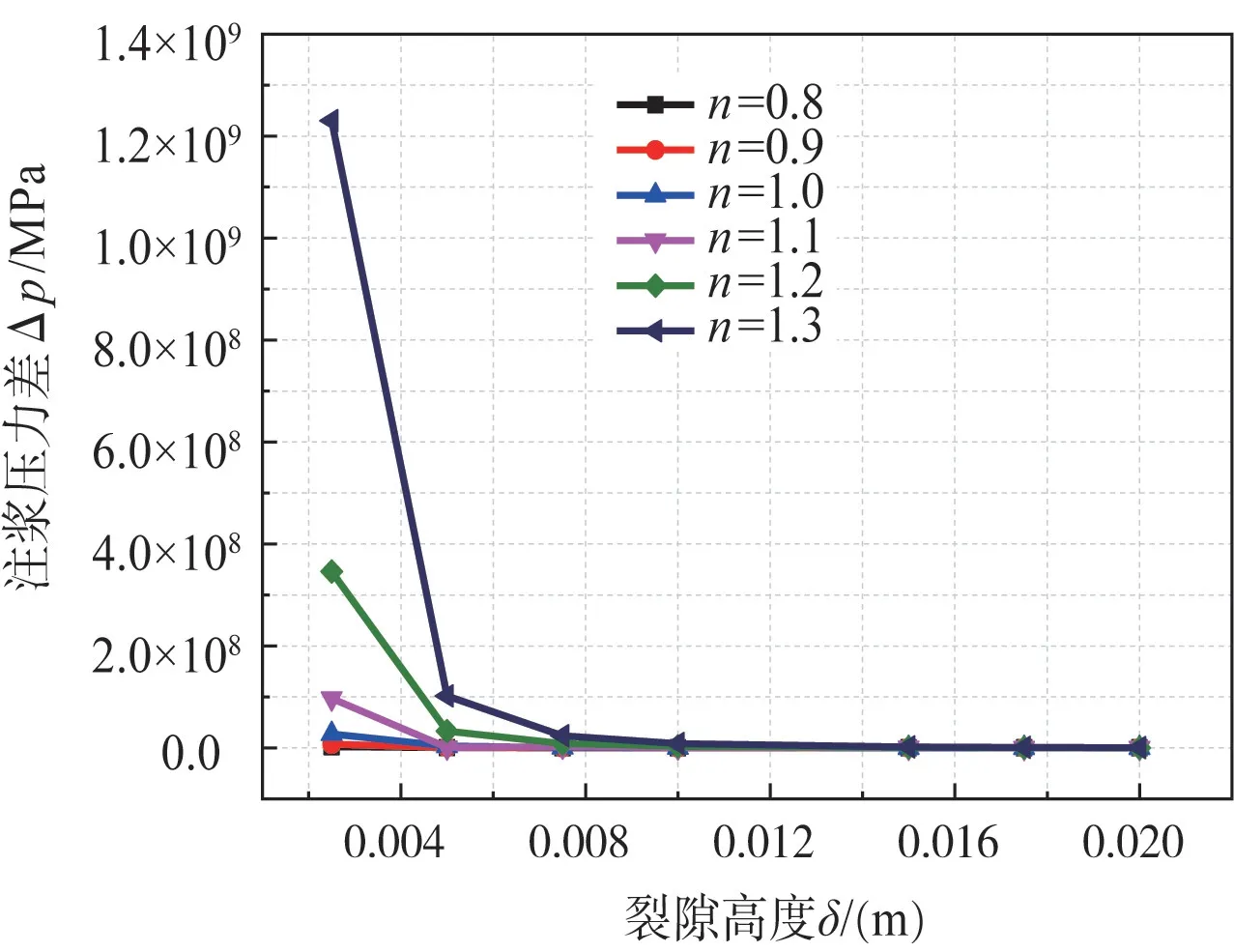
图4 裂隙高度对注浆压力差的影响Fig.4 The influence of the height of the crack on the grouting pressure difference

分析图3结果发现，在其他参数相同的条件下，裂隙高度δ增大到0.005时，浆体达到相应扩散半径所需注浆压力差ΔP也迅速降低；而流变指数n越小，δ的影响越不明显，即ΔP的降低幅度越小。而δ＞0.005时，ΔP的降低速度逐渐放缓，直至趋于不变。

（4）注浆压力差与注浆时间的关系

基于Herschel-Bulkley流体，针对注浆压力差ΔP的改变，取不同流变指数n，其他参数取值如表2，研究注浆时间t的影响。根据式（19）进行计算，注浆压力差ΔP值如图4所示。

分析图5结果发现，在其他参数相同的条件下，注浆时间t与压力差ΔP呈正相关。当t＜6 min时，注浆时间的影响不明显，此时注浆所需压力不大；当t大于6 min时，注浆时间的影响显著，即注浆越到后期所需压力越大；而流变指数n越小，时间对注浆压力的影响越不明显，因为浆液水灰比增大；上述分析与实际相符。

图5 注浆时间对压力差的影响Fig.5 The influence of grouting time on grouting pressure difference

2.2 注浆扩散半径

（1）浆液最大扩散半径与注浆压力差、流变指数的关系

基于Herschel-Bulkley流体，针对浆液最大扩散半径Lmax的改变，取不同流变指数n，注浆时间t=3 min，初始稠度系数C0=10，其他参数取值如表2，研究注浆压力差ΔP的影响。根据式（19）进行计算，浆液最大扩散半径Lmax值如图6所示。

图6 注浆压力差、流变指数对浆液最大扩散半径的影响Fig.6 The influence of grouting pressure difference and rheological index on the maximum diffusion radius of grout

分析图6结果发现，在其他参数相同的条件下，压力差ΔP的增大和流变指数n的减小，均可提高浆液最大扩散距离；且n越大，扩散距离的增大幅度越小，此时注浆压力差ΔP的变化对浆体最大扩散半径Lmax的影响也越来越小。原因是当n大于1时，此时浆液水灰比较小，黏度较大不易扩散；当n小于1时，浆液可认为是带屈服值的拟塑性流体，在裂隙中更易流动，因此扩散半径较大。

（2）浆液最大扩散半径与注浆压力差、初始稠度系数之间的关系

基于Herschel-Bulkley流体，针对浆液最大扩散半径Lmax的改变，取不同初始稠度系数，流变指数n=0.2，注浆时间t=6 min，浆体时变系数w=0.01，其他参数取值如表2，研究注浆压力差的影响。根据式（19）进行计算，浆液最大扩散半径Lmax值如图7所示。

图7 注浆压力差、初始稠度系数对浆液最大扩散半径的影响Fig.7 The influence of grouting pressure difference and initial consistency coefficient on the maximum diffusion radius of grout

分析图7结果发现，在其他参数相同的条件下，浆液最大扩散半径Lmax与稠度系数K成反比，即稠度系数K越小，最大扩散半径Lmax越大，即黏度越小，浆液越容易扩散；浆液最大扩散半径Lmax与注浆压力差ΔP成正比，即ΔP越大，最大扩散半径Lmax越大。

（3）最大扩散半径与压力差、时变系数的关系

基于Herschel-Bulkley流体，针对浆液最大扩散半径Lmax的改变，取不同注浆压力差，注浆时间t=6min，其他参数取值如表2，研究时变系数w的影响。根据式（19）进行计算，浆液最大扩散半径Lmax值如图8所示。

图8 注浆压力差、浆体时变系数对浆液最大扩散半径的影响Fig.8 The influence of grouting pressure difference and slurry time-varying coefficient on the maximum diffusion radius of slurry

分析图8结果发现，在其他参数相同的条件下，浆体时变系数w由0.010增加到0.019的过程中，浆液扩散半径变化明显，且下降速度逐渐放缓；当w大于0.019时，此时继续增加，Lmax变化也不明显，直至趋近于0。

（4）最大扩散半径与裂隙高度的关系

基于Herschel-Bulkley流体，针对浆液最大扩散半径Lmax的改变，取不同流变指数，注浆时间t=6min，其他参数取值如表2，研究裂隙高度δ的影响。根据式（22）进行计算，浆液最大扩散半径Lmax值如图9所示。

分析图9结果发现，在其他参数相同的条件下，浆液最大扩散半径Lmax与裂隙高度δ成正比，且流变指数越小，裂隙高度δ对最大扩散半径Lmax的影响更为显著。裂隙高度的扩大，有利于浆液的流动，因此最大扩散距离也提高；而随着流变指数n的增大，水灰比减小，浆液变稠，此时增加裂隙高度δ也没有明显变化。

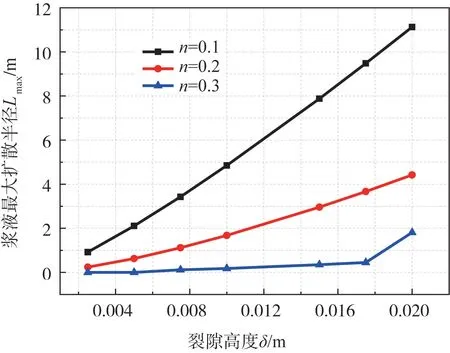
图9 裂隙高度对浆液最大扩散半径的影响Fig.9 The effect of the height of the crack on the maximum diffusion radius of the slurry

（5）浆液最大扩散半径与注浆时间的关系

基于Herschel-Bulkley流体，针对浆液最大扩散半径Lmax的改变，取不同流变指数，其他参数取值如表2，研究注浆时间t的影响。根据式（19）进行计算，浆液最大扩散半径Lmax值如图10所示。

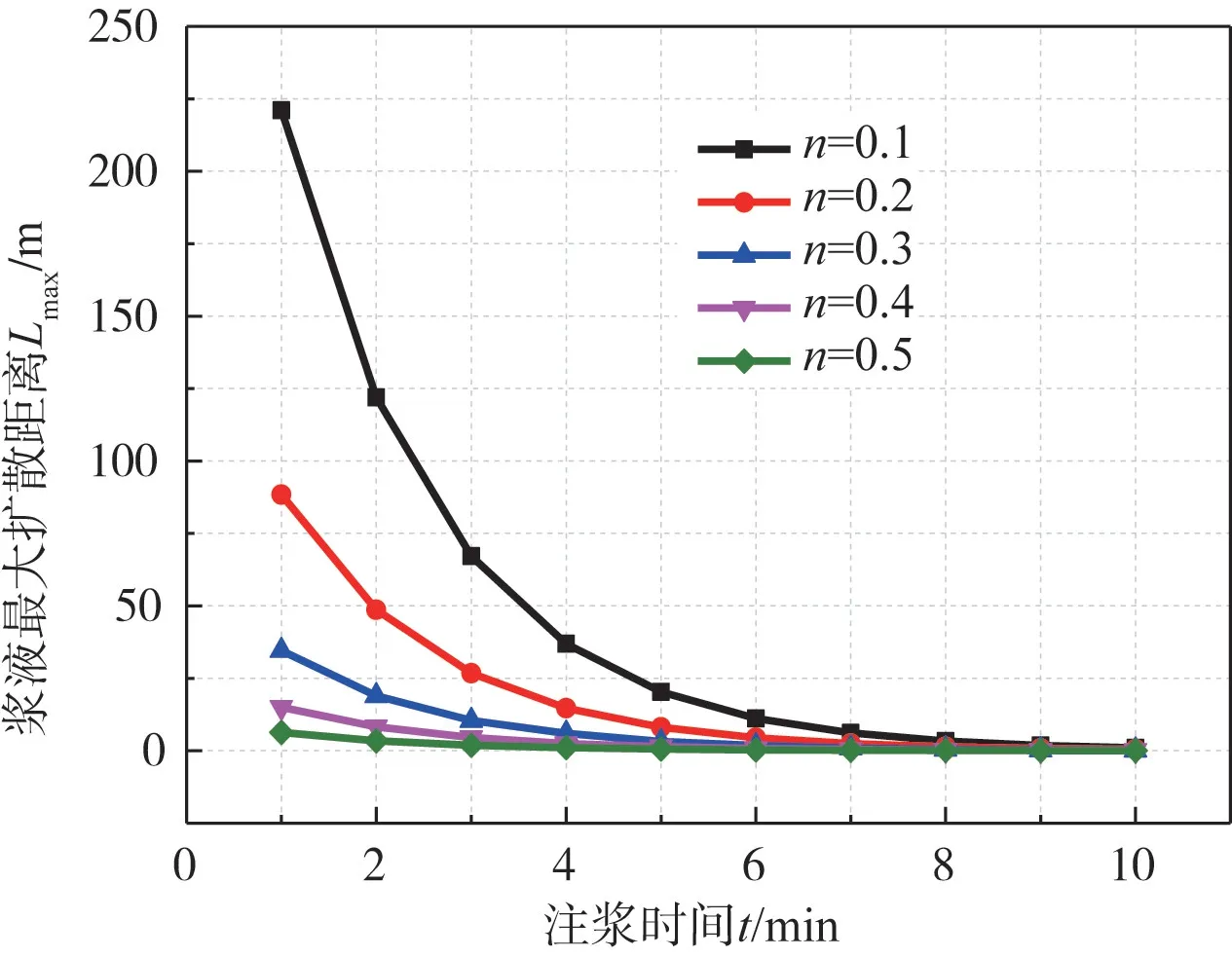
图10 注浆时间对浆液最大扩散半径的影响Fig.10 The influence of grouting time on the maximum diffusion radius of grout

分析图10结果发现，在其他参数相同的条件下，当注浆时间t=1 min时，此时浆液扩散半径最大；之后增大注浆时间，最大扩散半径变小。在同样的注浆时间里，增大流变指数n，最大扩散半径也减小，且半径减小的幅度逐渐下降，趋近于0。

3 公式计算结果对比

根据厦门隧道注浆试验数据［21］，大部分的地表冒浆都出现在距注浆孔1.5～2.5 m的区域内，而地表开裂冒浆位置可以表明注浆有效扩散范围（扩散半径）。

根据文献［21］中考虑黏度时变性的宾汉流体浆液扩散半径计算公式，对于平板裂缝理想平面流模型：在注浆压力差ΔP=0.15 MPa，流速υ=0.01 m/s，裂隙高度δ=0.01 m，初始稠度系数C0=15，浆体时变系数w=0.01，注浆时间t=20 min条件下，本文理论公式（19）计算出土体中浆液的最大扩散半径为2.2 m；而应用文献［21］中的公式计算得出的最大扩散半径为2.0 m，两者相差不大。由以上分析可知，文中公式（19）浆液扩散半径计算理论值在工程实测值范围内，可验证公式的正确性。