基于RF-PSO混合算法的边坡软弱夹层力学参数反演应用研究
2022-07-13胡斌汤琦李京丁静刘霁
胡 斌 汤 琦 李 京 丁 静 刘 霁
(1.武汉科技大学资源与环境工程学院,湖北 武汉 430081;2.冶金矿产资源高效利用与造块湖北省重点实验室,湖北 武汉 430081)
岩体的数值分析和计算方法已广泛应用于岩土 工程问题分析中。但由于地质条件的不确定性、施工的多变性和模拟实验存在取样困难、尺寸效应等问题,获取现场岩体的力学参数较为困难,使得构建好的数值计算模型,因力学参数选取的不合理而导致数值计算结果与工程实际存在较大差距。
Kavanagh等[1]最早提出了基于有限元法的弹性固体弹性模量反演方法,用来解决上述不足。而后伴随着人工智能技术的发展,优化方法出现了智能化的趋势,众多学者将各种智能算法与优化方法相结合起来,如人工神经网络、遗传算法、粒子群优化算法等被引入反分析中。冯夏庭等[2]通过遗传算法优化人工神经网络结构,并通过弹性问题的反分析,验证了方法的有效性。漆祖芳等[3]通过对传统粒子群算法的改进,提出了V-SVP-MVPSO算法,并成功地应用于大岗山水电站右岸边坡岩体参数反演分析中。王开禾等[4]通过将模拟退火算法(SA)很强的局部寻优能力与遗传算法(GA)相结合,用以提高算法的收敛速度及全局寻优能力。
以往的研究往往集中在对类神经网络算法的改进以及控制参数的优化来实现对工程现场的正确模拟反馈,通过不同算法性能的相互补充来解决早熟问题、局部最优以及鲁棒性等问题,从而实现精度上的提升,而往往忽视了算法选择的重要性。Chen等[5]通过对比研究了6种算法的预测性能,指出随机森林(RF)算法相较于单一的类神经网络算法(如BP神经网络、极限学习机(ELM)、支持向量机(SVM)等)存在控制参数少和泛化能力强的特点。故本文提出使用随机森林(RF)算法和粒子群(PSO)算法结合的RF-PSO混合算法模型,通过正交设计试验样本,与传统类神经网络模型进行对比后,获取岩体力学参数与监测位移之间的映射关系,完成对矿山边坡力学参数的反演。
1 计算方法与评价指标
1.1 计算方法
随机森林算法是一种集成学习算法[6-7],其原理如图1所示。它以决策树为基础,结合使用Bootstrap技术[8]和节点随机分裂技术,形成多棵决策树,最后将所有预测结果汇总输出。通过多棵决策树进行集成学习,有效地克服了单棵决策树容易出现过拟合精度较低等问题,并且有效降低了学习系统的泛化误差。
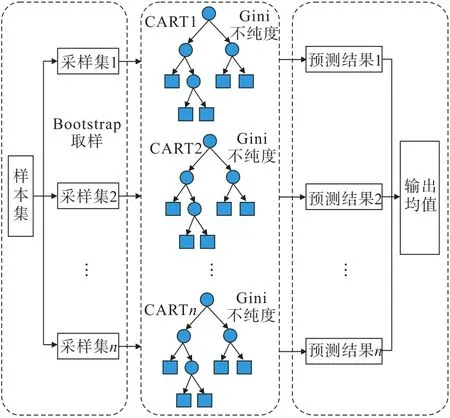
图1 随机森林算法示意Fig.1 Schematic of random forest algorithm
本文实现的随机森林算法是由以CART算法[9]为不纯度函数的决策树组成。采用Gini系数来选取合适的特征为切分点,使得模型可用于回归问题的分析,避免了传统的以信息增益为节点特征偏向于取值较多的属性的问题。
设数据集D={(x1,y1),(x2,y2),…,(xn,yn)}的属性空间X⊆Rm中某一特征变量Xj,j=1,2,…,m有q个取值,则Gini系数表达式如下:

式中,pi表示特征变量为i的概率。
粒子群算法(PSO)是由Kennedy J等[10]提出的一种群体智能优化仿生算法,通过不断迭代粒子的速度和位置信息,使模型达到目标问题的最优解。凭借具有输入参数少、收敛速度快、全局寻优能力强等特点,被广泛应用。
1.2 正交设计RF-PSO模型
正交设计RF-PSO模型是由正交设计构造试验样本、随机森林算法(RF)建立非线性映射关系和粒子群算法(PSO)对结果进行全局搜索三部分组成。具体算法流程如图2所示。
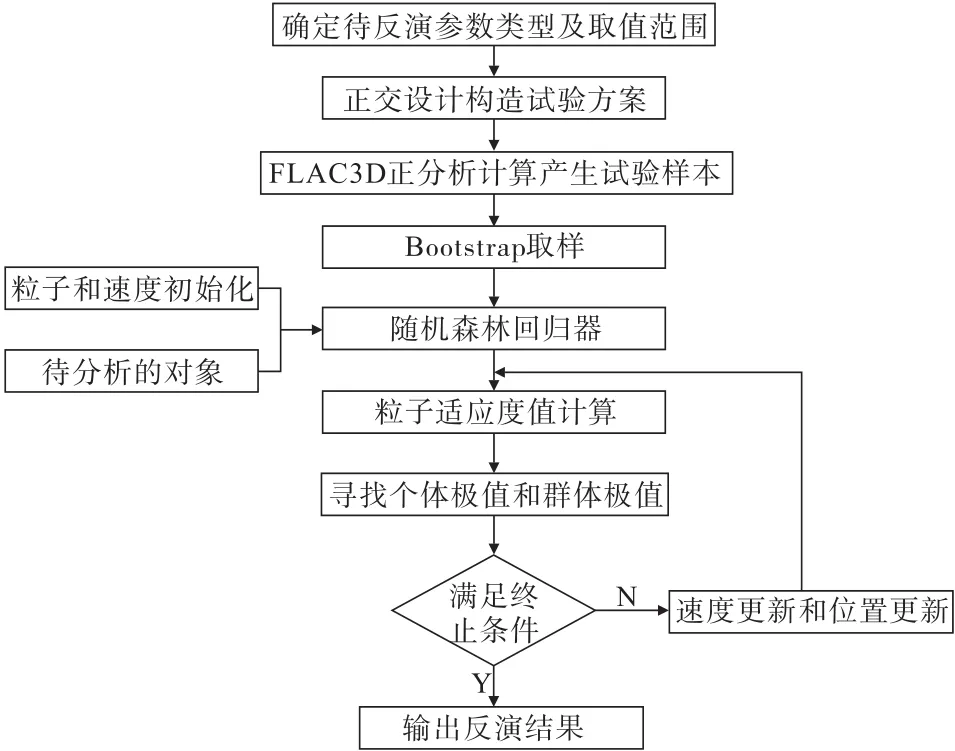
图2 正交设计RF-PSO混合算法流程Fig.2 Flow chart of RF-PSO hybrid algorithm with orthogonal design
基本步骤如下:
(1)确定待反演参数类型及取值范围。针对所要分析的问题确定反演参数类型及水平数,后根据正交设计构建试验方案,最后通过有限差分软件FLAC3D进行正分析计算位移后确定试验样本。
(2)采用Bootstrap取样,以形成与试验样本的相同的训练数据子集,进而形成回归预测决策树模型,生成随机森林模型。
(3)将训练好的随机森林模型与粒子群算法(PSO)相结合,凭借前者建立的映射关系及后者全局搜索能力,根据适应度函数不断更新粒子速度和位置,根据终止条件输出最优反演结果解。
1.3 性能评价指标
为了反映模型间的性能效果差异,结合Tseranidis等[11]总结的8种误差评价指标,选取平均绝对误差(MAE)、均方根误差(RMSE)和决定系数(R2)3个指标来评价模型回归效果的差异程度、离散程度和相关程度。

式中,ri、pi分别为监测点位移的计算值和预测值;n为输入数据个数;为监测点位移的平均值。
2 样本库构建
2.1 工程概况
以黄山某石灰石矿山边坡为研究对象,该石灰石矿山存在力学强度低、水理性质差的炭质泥页岩(软弱夹层),为边坡破坏的优势结构面。根据矿山开采设计,矿山边坡台阶坡面角为60°,最终边帮角为43°,台阶高度 15 m。
2.2 参数选取及试验方案设计
选取边坡软弱夹层力学参数作为模型的输入参数,查阅相关文献[12-14],搜集了11组软弱夹层力学参数,构建样本数据的多样性,用以提高模型对于软弱夹层力学参数与边坡位移的映射关系敏感度和反演力学参数的精度。为使样本数据安排合理具有科学性,采用L11正交表设计试验方案,FLAC3D正分析计算产生样本数据库。数据库建立好后,训练集占样本数据库80%,测试集占样本数据库20%。样本数据库中力学参数类型、变化范围及平均值如表1所示。

表1 软弱夹层力学参数数据范围Table 1 Mechanical parameter data range of weak interlayer
2.3 数值计算
选取该石灰石矿山采区典型剖面为计算模型进行正向计算,如图3所示。模型网格划分对于重点位置进行加密,其他位置采用合理网格进行过渡。监测点选择在边坡坡顶的位置,坐标为X=205.29 m,Z=170.61m,监测其由于石灰岩开挖后引起位移的大小。
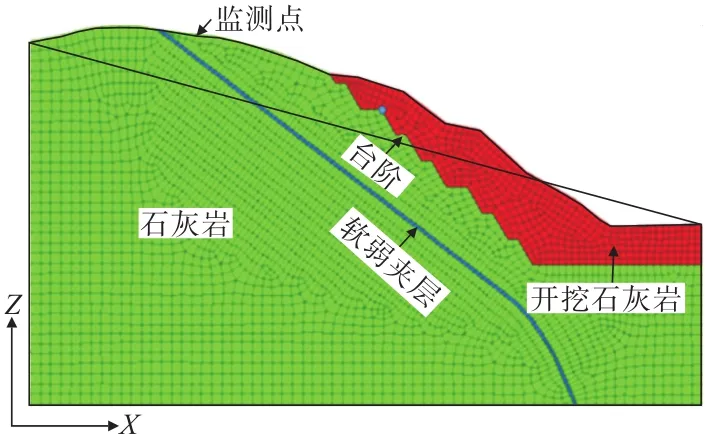
图3 优化后的边坡数值网络模型Fig.3 Optimized slope numerical network model
通过L11正交表设计方案设计的121组试验方案,通过FLAC3D软件进行数值计算,采用Mohr-Coulomb破坏准则。模型底部边界采用固定约束,侧向边界采用法向约束,采用自重应力作为初始地应力。由于监测点位于边坡顶部,故将监测点的竖向位移作为模型数据输出,样本数据共计121组。
如图4所示,数值计算结果主要分布在0~5.0 mm之间,样本的最大值及中位数分别为10.63 mm、1.21 mm,说明样本数据中存在少量的大位移点,可以作为后续检验模型预测泛化能力的参考。

图4 数值计算结果分布Fig.4 Distribution of numerical calculation results
3 模型对比分析
为了对比不同机器学习算法在矿山边坡力学参数预测上的性能差异,本研究选取BP神经网络模型和GA-BP神经网络模型作为RF算法的比较对象,模型搭建均在Matlab软件中进行。
3.1 模型参数的确定
根据输入层节点和输出节点数确定BP神经网络结构,由于数据和变量的数目较少,考虑采用单层的隐含层即模型中隐含层数为1,通过设置100组不同隐含层节点进行测试集精度分析,结果如图5所示,当BP神经网络结构为4-7-1时,误差数值最小。对于GA-BP算法模型中的遗传算法的群体规模N取10,遗传代数G取40,交叉概率PC取0.2,变异概率Pm取0.1,其他参数取系统默认值。
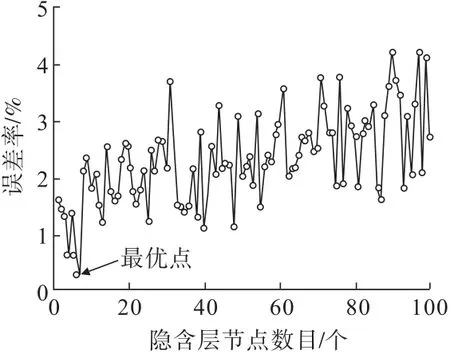
图5 BP神经网络模型性能和隐含层节点数目关系Fig.5 Relationship between the performance of BP neural network model and the number of hidden layer nodes
随机森林作为一种机器学习算法,决定其输出结果的因素主要为决策树数量及分裂属性个数。分裂属性个数一般设置为样本特征变量总数的66%[15],故本文中mtry等于3。ntree的值通过设置100个不同的值进行预测精度的分析,其结果如图6所示,当决策树数目为1时,对应的误差值最小。
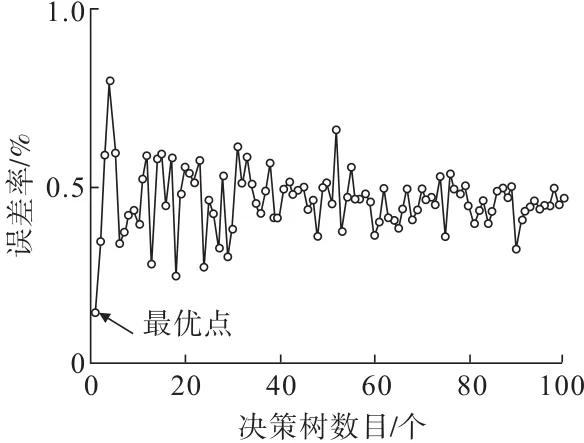
图6 RF算法模型性能和决策树数目关系Fig.6 Relationship between the performance of RF algorithm model and the number of decision trees
3.2 模型性能对比
选取数据集的80%(97组样本)作为训练集,20%(24组样本)作为测试集,以121×4矩阵作为输入数据,监测点Z方向位移作为模型输出,在Windows系统下,采用Corei7-9700F处理器进行运算,不同算法模型对测试集预测结果如图7所示。在运行速度上,BP神经网络模型凭借其结构简单运行速度最快,RF算法模型次之。通过MAE和RMSE的数值对比,RF算法模型凭借集成学习的特点其预测数据拟合度最好,混合算法模型GA-BP通过对神经网络中权值阈值的优化,在预测数据离散和差异程度上要优于单一的BP神经网络。在预测结果相关性上,RF算法模型也优于混合算法模型GA-BP及单一的BP神经网络,决定系数R2为0.96。
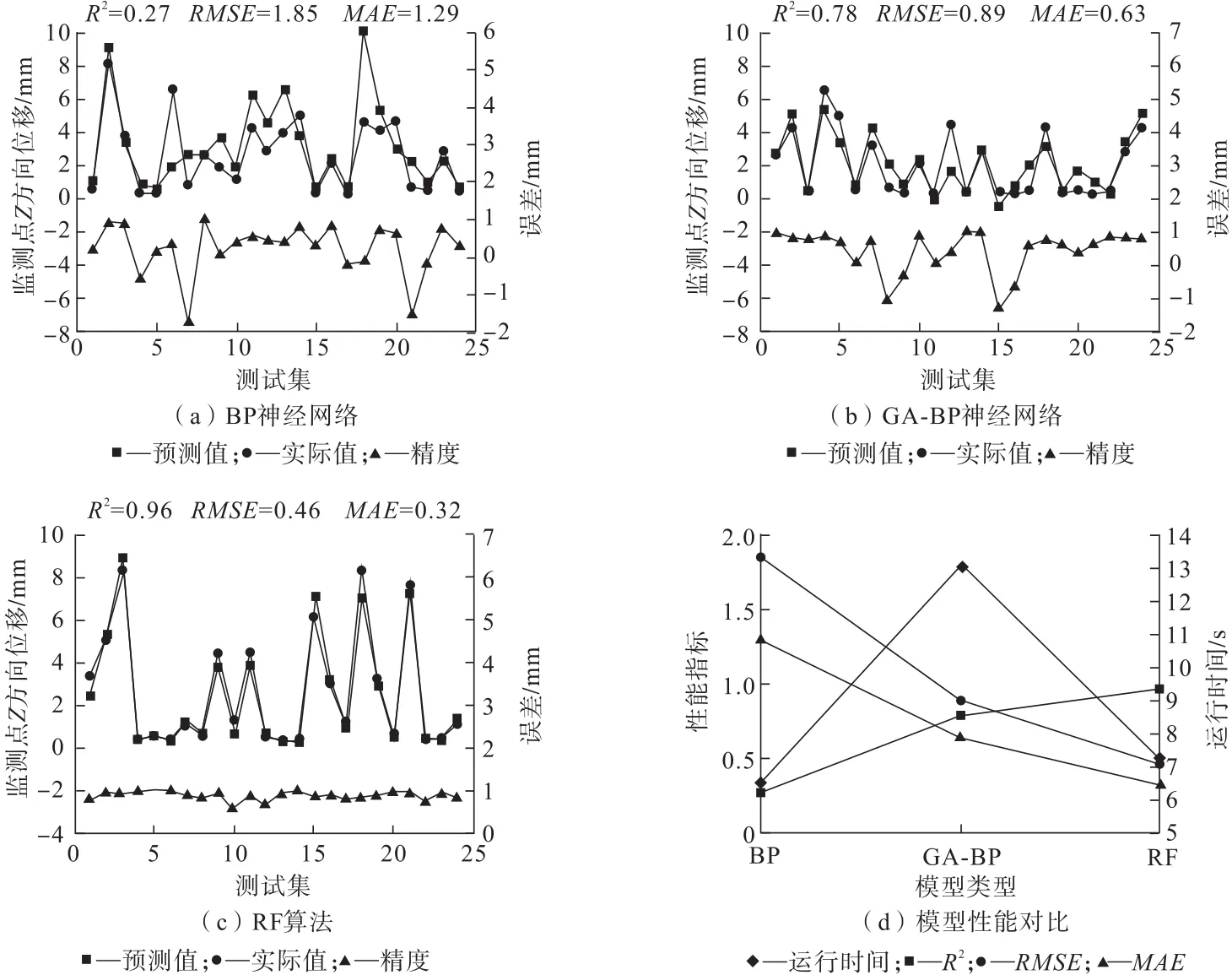
图7 模型的测试集预测结果Fig.7 Prediction results of test set of the model
由于数据集中大位移样本数量较少,导致BP神经网络和GA-BP神经网络模型对于大位移的预测出现了较大的误差,反之RF算法模型对于大位移的预测出现了较好的泛化能力,适合用来预测不同力学参数下的位移变化这一复杂的非线性问题。在精度波动上,RF算法也表现出集成学习算法波动小的特点。在可操作性上,RF算法模型控制参数数量较之传统的BP神经网络模型少,操作难度较小。GA-BP神经网络模型克服了控制参数选取的问题,但较之于随机森林(RF)算法模型,存在计算量大,运行速度慢的缺点。
因此,采用随机森林(RF)算法模型构建力学参数与位移间的映射关系。
3.3 基于反演结果的正分析与比较
将通过FLAC3D正向计算组成的样本集训练好的RF模型作为PSO算法中的适应度计算函数,采用量测值与预测值之间的绝对误差作为目标。选取4组位移值作为力学参数反演的对象,再将反演的力学参数结果导入已经建立好的数值计算模型中,判断算法的回归预测性能。为使反演结果具有的参考性和可对比性,根据样本数据的离散程度,选取4组位移:10、2.5、1.21、0.3 mm,分别进行反演分析计算,其结果如表2所示。从计算结果可以看出,除去大位移因为相关样本数据量不足反演结果出现较大偏差外,其余测试精度均达到95%以上。说明RF-PSO混合算法模型获得的参数和计算模型的合理性,其反演得到的力学参数可以模拟矿山边坡开挖后变形预测的正确性和有效性。
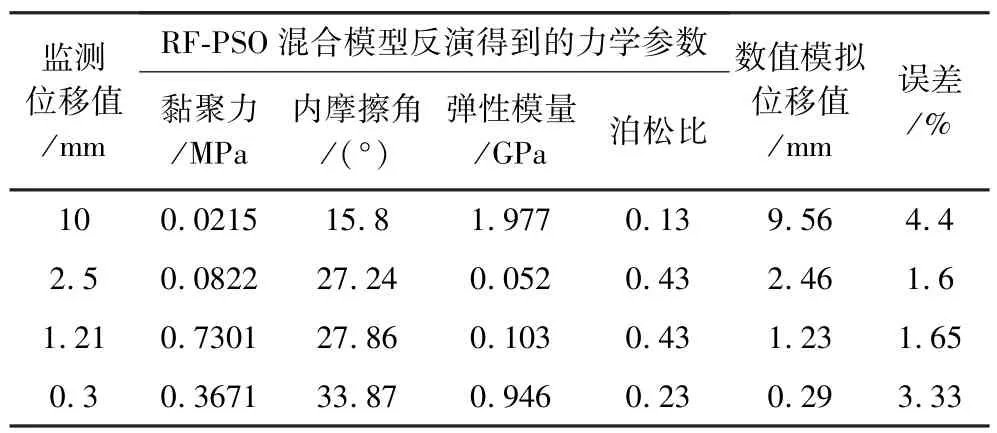
表2 岩石力学参数反演计算结果Table 2 Inversion calculation results of rock mechanics parameters
4 结 论
(1)RF-PSO混合算法与传统类神经网络模型相比较,在数据过拟合和泛化性方面较传统BP神经网络和GA-BP神经网络有大幅度提高,避免了过学习问题,提高了反演精度。运算速度也快于GA-BP神经网络模型,为智能反演提供了新的思路。
(2)以黄山某石灰石矿山边坡为计算模型所构建的样本集,应用RF-PSO位移反分析算法反演边坡软弱夹层力学参数后,进行正向计算的结果与实际值间的平均相对误差在3%左右,表明反演得到的软弱夹层力学参数是合理的。
