BBR拥塞控制算法的RTT公平性优化

潘婉苏，李晓风 ，谭海波，许金林，李皙茹

(1.中国科学院 合肥物质科学研究院，合肥 230031;2.中国科学技术大学，合肥 230026)

TCP拥塞控制对于互联网及其应用的发展和成功起到了重要作用。常用的拥塞控制算法是基于丢包反馈来调节拥塞窗口(congestion window，CWND)的大小，如Reno、BIC、CUBIC等算法[1-3]。但在高速、长距离的现代网络中，基于丢包的算法会造成吞吐量严重下降，往往会浪费很多可用带宽[4]。2016年Google提出了BBR(bottleneck bandwidth and round-trip propagation time)算法[5]，通过对瓶颈带宽和往返传播时间的估测来调整其发送行为，实现了高吞吐量的同时减少了传输延迟。Google公布的实施情况和一些公开发表的评测结果[6-11]表明，BBR可以显著提高TCP连接的吞吐量，与传统CUBIC相比在吞吐量上具有显著优势，但BBR仍存在着一些缺陷，其中RTT(round trip time)公平性问题是比较严重的问题之一。即当多个数据流共享同一瓶颈链路时，RTT较长的BBR数据流具有带宽占用优势[7,12-15]。

针对RTT公平性问题，一些学者进行了改进。文献[7]提出了BBQ算法，通过限制RTT较长的数据流的检测周期来降低长RTT流的带宽占用。当T>(1+β)Tprop时(T为RTT，Tprop为RTprop，即round propagation time)，使用min(α;Tprop)作为探测周期的持续时间，从而减小长RTT流发送的数据包数量，其中β∈[0.5%,1%]，α=3 ms。文献[12]通过建立理论模型证明了不同RTT流带宽占用受RTT比率的影响，长RTT流的带宽占比具有优势。文献[13]提出了RFBBR算法，在PROBE_BW阶段添加公平性因子γ=(T+Tprop)/(2×T)调节拥塞窗口的大小，进而改进RTT公平性。文献[14]提出了延迟感知BBR(delay-aware BBR，DA-BBR)算法，根据RTT定义一个小于1的调节因子去限制链路中的带宽时延积(bandwidth delay product，BDP)，缓解了RTT不公平性。文献[15]提出通过调整拥塞窗口增益缩小不同RTT流之间的窗口差距，从而提升RTT公平性。以上这些算法在提高RTT的公平性方面取得了一定积极的效果，但分析发现，现有的这些改进方案都限制了BBR流的探测，并且仍采用固定的起搏增益，而未对起搏增益这一关键参数进行优化。

本文对BBR算法的探测过程进行建模分析，利用RTT反馈调节BBR在探测带宽状态中的起搏增益，建立起搏增益模型去平衡不同流之间的发送速率，从而提升不同RTT流之间的公平性。网络模拟器3(network simulator 3，NS3)的仿真实验表明，改进算法BBR-adaptive(BBR-A)有效提升了算法的RTT公平性以及其他方面的性能。

1 BBR算法概述

1.1 基本原理

不同于基于丢包的拥塞控制算法，BBR算法通过交替测量链路中的最大带宽和最小延时来解决寻找Kleinrock最佳操作点[16]的问题。BBR将最近10次往返中测得的最大带宽视为Bmax，将过去10 s中测得的最小延时视为Tprop，然后根据Bmax和Tprop估算BDP[16]，即

BBDP=Bmax×Tprop

(1)

BBR分别通过窗口增益和起搏增益来调整CWND和发送速率，进而控制其发送行为。CWND和发送速率的计算公式为

Wcwnd=cwnd_gain×BBDP

(2)

S=pacing_gain×Bmax

(3)

式中:Wcwnd为CWND，cwnd_gain为窗口增益，S为发送速率，pacing_gain为起搏增益。

BBR主要由4个状态构成，见图1。

图1 BBR的状态模型Fig.1 State model of BBR

在STARTUP状态，将cwnd_gain和pacing_gain设置为2/ln 2，使CWND和发送速率指数增加，积极的探测链路中的可用带宽。如果连续3个RTT内新估算的带宽增加没有超过25%，BBR则进入DRAIN状态。在DRAIN状态，BBR通过将pacing_gain降低到ln 2/2来清除前一状态的剩余队列，cwnd_gain保持不变(2/ln 2)。在PROBE_BW状态，BBR循环8个周期(pacing_gain[]=[1.25;0∶75;1;1;1;1;1;1])进行探测带宽，每个周期持续时间为Tprop。在这个状态中CWND固定为2BBDP。BBR每10 s进入一次PROBE_RTT状态，在这个状态CWND被设置为4MSS(Maximum Segment Size)，以确保对Tprop新值进行采样，该状态持续200 ms。在PROBE_RTT状态结束后，通过瓶颈链路状态判断转换到PROBE_BW或STARTUP状态继续进行循环。

1.2 RTT公平性原因分析

在PROBE_BW状态，BBR周期性地以pacing_gain=1.25增加发送速率，向瓶颈链路发送更多的数据包，导致总发送速率大于瓶颈带宽，在瓶颈上形成了持久队列。随后pacing_gain=0.75降低发送速率，试图排空先前探测生成的多余的队列。但这种循环实际无法排空多余的数据，仍然会形成队列积压。根据排队论，一旦在瓶颈处形成持久队列，不同数据流的吞吐量就取决于它的队列份额。

当不同RTT流通过瓶颈链路时，长RTT流的BBDP估算值大于短RTT流的BBDP估算值，其可以发送更多数据包，因此在瓶颈队列中占主导地位。长RTT流的队列份额优势可以让其获得比短RTT流更高的发送速率，使短RTT流的发送速率不断降低。持续的低传输速率将导致短RTT流在下一次带宽测量中获得更小的BBDP估算值，然后再次降低发送速率，又将进一步减少其队列，循环往复，最终导致短RTT流的带宽占用严重下降。即使在探测过程中的一些数据流提前终止，上面的结论仍然成立，因为其他数据流将很快抢占空闲带宽。随着数据流RTT差异的增加，公平性会进一步恶化。一些用户可能利用这个漏洞故意增加延迟去获得高带宽。因此，解决BBR算法中RTT公平性问题是非常必要的。

2 改进算法:BBR-A

2.1 模型分析

通过本文RTT公平性分析可以知道，队列积压的产生导致长RTT流的发送速率大于短RTT流。对BBR流建模，分析RTT与发送速率之间的关系。假设有n个不同数据流通过带宽为C的瓶颈链路，fii∈[1,n]为第i个数据流，di(t)为fi在t时刻的传递速率，在t时刻fi的估算最大带宽为

Bmaxi(t)=max(di(t))(T∈[t-10RRTT;t])

(4)

在实际传输过程中，RTT由传播时延和排队时延组成，fi在时间t时刻的RTT为

Ti(t)=qi(t)+Tpropi

(5)

式中qi(t)为fi在t时刻的排队时延。

设Ii(t)为fi的飞行中数据量，则Ii(t)与di(t)关系为

(6)

进一步分析RTT与起搏增益之间的关系，根据BBR算法的带宽探测机制，在向上探测周期pacing_gain=1.25，因此在t时刻最大传递速率为

(7)

BBR流的探测周期为8个Tprop，结合式(7)可以知道fi在新一轮最大带宽估算时更新为

(8)

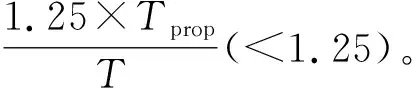
2.2 算法设计

为了平衡不同RTT流的带宽占用，可以在现有增益系数基础上乘上一个RTT的减函数来消除RTT对发送速率的影响。如果一个长RTT数据流，那么其发送速率缓慢地向上增加并且快速地向下减少。如果一个短RTT数据流，那么它的发送速率应该快速地向上增加并且缓慢地向下减少，从而实现起搏增益系数对发送速率的约束。根据RTT的测量机制，将φ定义为fi当前延时与最大延时比值，计算公式为

(9)

式中：Ti为fi从最后一个ACK中获得的当前延时，Tmax为ACK更新的最大延时。

通常φ可以量化瓶颈的链路利用率[17-18]，Ti越大，φ越大。仅在瓶颈链路容量和缓冲区即将满载时，Ti才接近最大的Tmax。通过φ构建关于RTT的减函数作为新的向上和向下起搏增益系数，进而约束不同RTT流的发送速率。

基于上述分析，分别定义了向上起搏增益系数Pup和向下起搏增益系数Pdown来替代固定的起搏增益系数1.25和0.75。对于Pup，相关函数Pup(φ)应该为一个下凹的曲线，下渐近线为Pup=1，并且随着φ变大，Pup(φ)下降趋势变缓，以减少优势数据流的发送速率，给弱势数据流提供更多的可用带宽。对于Pdown，相关函数Pdown(φ)应该为上凸的曲线，上渐近线为Pdown=1，并且随φ越大，Pdown(φ)下降趋势变快。此外，Pup(φ)和Pdown(φ)所需函数必须为低复杂度的函数，因为它要在BBR算法内核中实现。基于这些约束条件，测试了一些函数，发现反比例函数可以满足需要。基于反比例函数的特性，构造了Pup(φ)和Pdown(φ)

(10)

(11)

Pup函数和Pdown函数的变化趋势见图2。随着φ的增大，Pup(φ)缓慢下降，且下降趋势变慢，取值在[1,1.5]之间；随着φ的增大，Pdown(φ)缓慢下降，且下降趋势变快，取值范围在[0.5,1]之间，满足增益模型的设计需求。BBR-A算法通过每个ACK更新RTT的信息调整原BBR中起搏增益的大小，从而自适应调节发送速率。此外，根据BBR的探测机制，将链路状态的分界点设置为1.25BBDP[19]。BBR-A具体细节见算法1，当Ii<1.25BBDP时，允许不同RTT流发送更多的数据包来占用空闲带宽。在这个向上探测周期内，采用pacing_gain=Pup来增加发送速率。当飞行中的数据量大于1.25BBDP时，表明瓶颈链路没有额外的能力来传输更多的数据包，并会在缓冲区形成队列，此时通过pacing_gain=1维持稳定的发送速率。此外，为了增加BBR算法对丢包的敏感性，增加丢包阈值has_loss(阈值设定2%)表示是否存在严重丢包。如果Ii>1.25BBDP并且有丢包产生，此时的向下探测周期要限制不同RTT流的发送速率，采用pacing_gain=Pdown降低发送速率，释放缓冲区。剩余周期，BBR-A依然采用原BRR中默认的pacing_gain。

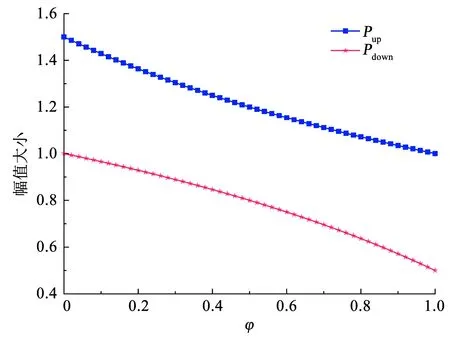
图2 BBR-A算法中Pup和Pdown函数随着φ的变化趋势Fig.2 Variation of Pup and Pdown functions with φ in BBR-A algorithm

BBR-A算法通过对起搏增益的调节，进一步增强了不同RTT流发送速率的自我调节能力。将带宽探测状态的向上起搏增益系数上限扩大到1.5，提高BBR的探测带宽幅度，同时将向下起搏增益系数下限设置为0.5，加快多余数据包的排空。通过让不同RTT流的探测和排空系数彼此交错，可以平衡不同数据流的发送速率，从而提高RTT公平性。

参考文献[13]进行BBR-A算法的复杂度分析，BBR-A采用if循环语句判断链路状态，因此其时间复杂度为O(1)。BBR-A每个周期只存储起搏增益的计算结果，没有额外的内存消耗，其空间复杂度也为O(1)。另外，BBR-A算法的实现依旧基于原有的BBR框架，便于实施与部署。

3 实验结果分析

基于BBR版本[20-21]在NS3上测试了BBR及优化算法的性能，网络拓扑见图3。S0～Sn为发送端，R0～Rn为接收端，瓶颈带宽设置为100 Mbit/s。

图3 仿真模拟实验的网络拓扑Fig.3 Network topology of simulation experiment

通过不同网络条件下测试所获得的仿真结果验证BBR-A算法有效性。性能指标包括吞吐量、信道利用率、Jain公平指数和重传率，变量包括RTT和缓冲区大小。此外，将BBQ[7]和DA-BBR[14]作为基准算法加入到实验对比中。

3.1 信道利用率

信道利用率表示信道平均被占用的程度，可以一定程度反映网络利用率。通常通过测量数据流的吞吐量来计算瓶颈链路的信道利用率η，即

(12)

式中:Qbytesi为fi在接收端已接收数据包的长度，C为瓶颈链路的带宽，Tlast为持续的模拟运行时间(本文设定为200 s)。

由于BBR算法在高丢包率下容易失速，因此本节测试具有不同随机丢包率下的信道利用率，以评估算法的抗丢包能力。缓冲区大小配置为1BBDP和5BBDP，随机分组丢失率分别设置为0%、1%、3%和6%。

BBR、BBQ、DA-BBR和BBR-A算法的信道利用率的仿真结果见图4。整体来看，4种算法在1BBDP缓冲区的信道利用率要低于5BBDP缓冲区。当随机丢包率为0%时，4种算法可以在不同的缓冲区中获得94%以上的信道利用率，其中BBR-A信道利用率最高，1BBDP和5BBDP缓冲区中分别为95.6%和96.2%。4种算法的信道利用率均随着丢包率的增加而降低，但BBR-A受丢包的影响相对较小。当随机丢包率为6%时，BBR的信道利用率明显下降，而BBR-A的信道利用率降幅最小。BBR-A算法加入了丢包反馈，并提高了起搏增益上限，可以在不同的缓冲区始终保持90%以上的信道利用率，尤其在高丢包的场景中获得更高的吞吐量。

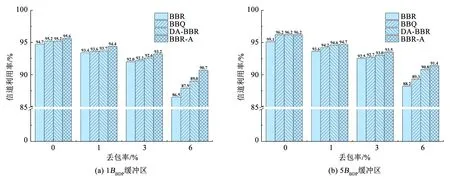
图4 4种算法的信道利用率Fig.4 Channel utilization of four algorithms

3.2 RTT公平性

通过比较BBR、BBQ、DA-BBR和BBR-A算法不同RTT流之间的吞吐量，评估BBR-A是否缓解了RTT不公平性。实验设置0.5BBDP和5BBDP缓冲区大小，10 ms RTT流与50 ms RTT流竞争瓶颈带宽。图5为10 ms RTT流和50 ms RTT流的吞吐量对比。

对于BBR算法，2种缓冲区中10 ms RTT流和50 ms RTT流的吞吐量见图5(a)和5(e)。在启动阶段10 ms RTT流可以快速获得吞吐量，但与50 ms RTT流短暂竞争后，其吞吐量快速下降，最终约为39.7 Mbit/s，而50 ms RTT流吞吐量是其1.4倍。在图5(e)中，2种RTT流的吞吐量差异明显变大，10 ms RTT流的吞吐量仅为13.8 Mbit/s左右，50 ms RTT流吞吐量是其5.9倍。图5(b)和5(f)为BBQ算法，在0.5BBDP缓冲区中2种RTT流的吞吐量差异相比BBR算法变小。10 ms RTT流的吞吐量提高到42.3 Mbit/s左右，50 ms RTT流的吞吐量约是其1.3倍。在5BBDP缓冲区(图5(f))，2种RTT流之间的吞吐量差异比图5(b)中的结果有所增加，50 ms RTT流的吞吐量为59.3 Mbit/s，是10 ms RTT流的1.6倍。DA-BBR算法见图5(c)和5(g)，2种缓冲区中数据流的吞吐量差异变化不大，50 ms RTT流的吞吐量约是10 ms RTT流的1.3倍。对于BBR-A算法，在0.5BBDP缓冲区(图5(d))，10 ms RTT流和50 ms RTT流的吞吐量差异相比前3种算法进一步缩小。10 ms RTT流和50 ms RTT流吞吐量分别为45.3 Mbit/s和50.3 Mbit/s，相差10%。在5BBDP缓冲区(图5(h))，10 ms RTT流的吞吐量波动相对较大，说明数据流积极地竞争可用带宽，50 ms RTT流的吞吐量约是10 ms RTT流的1.3倍。

图5 不同算法在不同缓冲区中10 ms RTT和50 ms RTT流的吞吐量对比Fig.5 Throughput comparison of 10 ms RTT flow and 50 ms RTT flow with different algorithms and buffer sizes

通过图5的对比结果可以看出，与BBR相比，BBQ提高了2种RTT流之间的公平性，但在5BBDP缓冲区，50 ms RTT流的吞吐量优势依旧明显。而DA-BBR算法也提高了2种RTT流之间的公平性，尤其是在5BBDP缓冲区中相比于BBQ算法有了进一步提升。BBR-A改变了不同RTT流的起搏增益，提高了短RTT流的带宽竞争能力，缩小2种RTT流的吞吐量差异，在4种算法中实现了最好的RTT公平性，尤其在0.5BBDP缓冲区中具有明显公平性优势。

另外，通过上述实验结果发现不同的缓冲区大小对RTT的公平性有着明显的影响，因此继续开展相关实验比较10 ms RTT流和50 ms RTT流在不同缓冲区中的性能差异，进一步评估4种算法的RTT公平性。为了量化算法在不同缓冲区大小下的RTT公平性，本文引入了Jain公平指数[22]。Jain公平指数可以用来衡量带宽竞争中的公平性，计算方法如下：

(13)

式中:n为链接个数，xi为第i个链接的吞吐量。

Jain公平指数(以下简称公平指数)能够很好地反映吞吐量的差异，取值范围在[0,1]之间。该公平指数越接近1，说明带宽分配的公平性就越好。

10 ms RTT流和50 ms RTT流在0.1BBDP～100BBDP的缓冲区条件下，各自的平均吞吐量变化和公平指数见图6。图6(a)为BBR算法，随着缓冲区变大，2种RTT流的吞吐量差异变大。当缓冲区大于6BBDP，50 ms RTT流占用大部分带宽，公平指数下降到0.63左右。对于BBQ算法，见图6(b)。相比BBR，其公平性得到了很大的提升。虽然2种数据流竞争时吞吐量差异随着缓冲区变大而加大，公平指数也随着下降，但BBQ的公平指数仍能维持在0.91以上。图6(c)中的DA-BBR算法，其公平指数最小维持在0.95左右。在图6(d)中，BBR-A算法明显缩小了10 ms RTT流和50 ms RTT流的吞吐量差异，其公平指数维持在0.96以上。总体而言，BBR-A比BBR和BBQ算法RTT公平性更好，比DA-BBR算法略有优势。尤其在深缓冲区条件下，RTT公平性相比BBR算法有了很大的提升，公平指数提高了约1.5倍，实现了更好的性能。

图6 不同缓冲区大小下，10 ms RTT流与50 ms RTT流竞争时的平均吞吐量和公平指数Fig.6 Average throughput and fairness index of 10 ms RTT flow competing with 50 ms RTT flow with different buffer sizes

除了缓冲区大小对RTT公平性有着明显的影响，RTT差异也会明显影响RTT公平性[13]。仿真设置10 ms RTT流与不同RTT流在5BBDP缓冲区条件下进行带宽竞争，4种算法中不同RTT流的吞吐量的变化趋势和公平指数见图7。

图7 5BBDP缓冲区大小下，10 ms RTT流与不同RTT流共存时的平均吞吐量和公平指数Fig.7 Average throughput and fairness index of 10 ms RTT flow coexisting with different RTT flows in 5BBDP buffer

图7(a)为BBR算法，随着RTT差异的增加，长RTT流的吞吐量逐步占据优势，公平指数逐步下降。当RTT比率达到10倍时，即10 ms RTT流与100 ms RTT流竞争时，公平指数仅为0.59。在图7(b)中，BBQ算法中的RTT公平性呈现不规律变化。当RTT比率在2～3之间时，短RTT流的吞吐量占据优势地位，但当RTT比率大于3时，长RTT流的吞吐量逐步占据优势地位。图7(c)的DA-BBR算法，不同RTT流之间的公平性有所提升，最终公平指数在0.92左右。BBR-A算法见图7(d)，随着RTT差异的增加，虽然长RTT流的吞吐量占据优势，但其与10 ms RTT流之间的吞吐量差异不大，BBR-A的公平指数可以维持在0.95左右。BBR-A算法通过自适应的调整不同RTT流之间的起搏增益，可以使不同RTT数据流保持较高的公平性，尤其当RTT比率大于4时，BBR-A算法的公平指数最高。

3.3 重传率

重传率是重传网络包的比例，链路中的重传率过高一般表示网络质量差，会影响数据的传输效率。通过对比缓冲区大小和竞争数据流的数量对数据包重传的影响，可以验证不同算法的重传率。实验发送方使用不同的算法将单个或多个数据流传输到接收方，缓冲区大小设置分别为0.1BBDP和1BBDP。4种算法的重传率见图8，起始点为单个10 ms RTT流的重传率，终点为100个10 ms RTT流的重传率。

图8 不同算法在不同缓冲区中的重传率Fig.8 Retransmission rates of different algorithms with different buffer sizes

在图8(a)中，当缓冲区为0.1BBDP时，BBR的重传率明显高于其他算法。在起始点，BBR的重传率约为2.8%，BBQ、DA-BBR和BBR-A的重传率约为1.52%、1.26%和1.31%。随着数据流量的增加，数据包出现了大量的重传，当流的数量为100时，BBR、BBQ和DA-BBR的重传率分别为14.9%、6.01%和4.86%，而BBR-A的重传率约为4.24%，是4种算法中最小的。在图8(b)中，缓冲区大小增加到1BBDP。BBR的重传率相比0.1BBDP时明显下降，但仍是4种算法中最高的。在起始点，4种算法的重传率基本一致，大约为1%。随着流的数量的增加，4种算法重传率都发生了增加。当数据流的数量为100时，BBR的重传率约为4.63%，BBQ和DA-BBR的重传率约为3.95%和3.52%，BBR-A的重传率约为3.42%。BBR-A算法加入了丢包反馈，并建立对称的起搏增益模型，避免激进的探测带宽方式导致的数据包重传。仿真实验结果证明了BBR-A算法可以减少数据包重传次数，有效提高网络通信效率。

4 结 论

本文在研究BBR拥塞控制算法的基础上，针对原BBR算法中的RTT公平性问题，提出了改进算法BBR-A。BBR-A算法根据链路中的RTT，自适应调整向上和向下起搏增益，取代了原有的固定起搏增益，从而平衡不同RTT流的发送速率。

NS3仿真实验结果表明，BBR-A算法中不同的RTT流可以公平竞争，公平指数明显高于BBR。此外，在信道利用率的实验中，与原BBR算法相比，BBR-A算法并没有牺牲信道利用率，甚至在高丢包的情况下信道利用率提升明显。在重传率的实验中，BBR-A算法的表现也优于BBR算法，可以有效降低重传率。这些都表明本文提出的BBR-A算法可以有效提升BBR算法的网络拥塞控制性能。