基于免疫克隆算法的一阶磁梯度张量定位方法
2022-07-13向枫桦杨宾锋郭娇娇
向枫桦, 杨宾锋, 李 博, 赵 震, 郭娇娇
(空军工程大学信息与导航学院,西安,710077)
目前,关于定位的手段和方法有诸多种,但是许多定位方法都有一个局限性,就是容易被干扰。另外,在一些特殊的场合,例如室内、地下、水下以及一些其他的复杂环境,诸多导航定位手段就无法应用[1-3]。无线电导航系统可以实现飞机的进场和着陆保障,但信号非常容易被干扰[4]。卫星导航可以实现高精度定位,但在室内等特殊场合无法接收到信号[5]。而磁场信号拥有穿透性强和抗干扰能力强的优点,可以应用在室内、地下等特殊场合[6]。因此,利用磁信号进行导航定位具有非常大的发展潜力。
关于磁信号定位的方法,目前有多种不同方法,其中梯度张量方法由于计算相对简单,因此应用也最广泛。对于梯度张量方法,国内诸多专家学者提出了不同的计算模型。邓国庆推导了一阶梯度张量定位机理,并将其应用在永磁体中,但传统的一阶梯度张量定位受地磁场和背景磁场影响大[7]。李青竹等推导了二阶梯度张量定位机理,由于地磁场和背景磁场的二阶梯度张量十分小,因此该方法可以提高定位精度,但是无法直接测量二阶梯度张量矩阵[8]。以上这些算法都是基于单磁偶极子推导,在远距离能够保持不错的测量精度,但是在距离较近或者磁源体积比较大时,单磁偶极子定位就存在误差大的不足,因此出现了许多误差补偿方法。袁鹏等运用梯度张量不变原理消除了椭圆误差,在正六面体测量阵列上有效提高磁信号的定位精度[9]。Wang等利用最小二乘法对磁信号进行优化处理并运用一阶梯度张量进行定位计算,结果表明能够有效提高定位精度[10]。为了解决梯度张量算法在进场定位误差大的不足,本文提出了基于免疫克隆算法的一阶磁梯度张量定位方法。
本文将免疫克隆算法融入到一阶磁梯度张量定位原理中,探究了新算法在进场时的定位精度。在一阶磁梯度张量定位原理的基础上,根据磁场衰减规律,提出了误差梯度矩阵的概念并推导了其计算方法。然后,利用免疫克隆算法对误差矩阵进行优化处理。为了验证新方法的有效性,在Matlab中采用了三条不同的路线进行计算并与一阶梯度张量定位算法进行对比分析。最后,通过无磁转台的旋转永磁体实际定位实验对算法的定位效果进行进一步的验证。研究发现:基于免疫克隆算法的一阶磁梯度张量定位方法在距离较近时,能够有效提高磁定位精度 。
1 一阶梯度张量定位原理
1.1 梯度张量矩阵
以磁偶极子为原点,建立空间坐标系,在距离磁偶极子任意一点r(x,y,z)的磁感应强度表达式为:
(1)
磁梯度张量是磁感应强度在不同方向的偏导数,包括一阶梯度张量和二阶梯度张量,可以反应磁场在不同方向的变化率,拥有大量的磁场信息。磁感应强度的三分量在3个轴向方向上的分量变化率就是一阶磁梯度张量矩阵[11],因此,一阶磁梯度张量矩阵一共有9个元素,记作G,如下式所示:
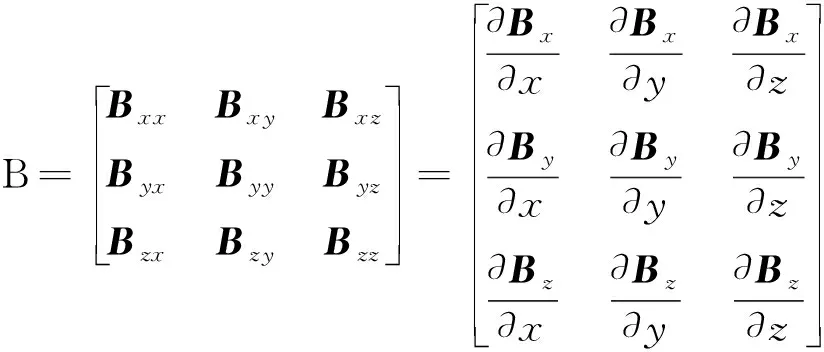
(2)
根据Maxwell方程组,磁感应强度的旋度和散度均为0[11],可以得到:
(3)
(4)
将式(3)展开化简,可以得到:
(5)
由式(5)可知一阶磁场梯度张量矩阵G满足4个关系式,有6个不同的量满足两两相等的关系,剩下3个量满足一个等式,也就是说要想知道梯度张量矩阵G,最少要知道5个量的值并且都是独立的量。
将式(1)中的磁场三分量分别进行求偏导数计算,可以得到9个梯度张量的理论值,只取5个独立元素的表达式为:
(6)
1.2 测量阵列
用于测量磁梯度张量的传感器模型有诸多种,其中十字形传感器精度最高[13]。如图1所示,该模型一共由5个参数一模一样的传感器组成,每个轴上都分布3个相同的传感器,其中0号传感器是公用的传感器。另外,任意相邻两个传感器之间的距离都相等,大小为d。
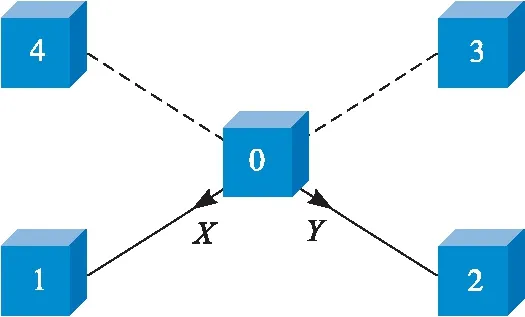
图1 十字形传感器
根据数值微分知识中的三点法求导方法,可以得到相应的偏导数为:
(7)
1.3 一阶梯度张量定位
磁场的欧拉反褶积方程为:
(8)
式中:H为磁感应强度;P为环境噪声;k为常数。对于磁偶极子来说,k的值为3[14]。因此可以得到磁场的定位表达式为:
(9)
1.4 误差理论分析
如图2所示,十字形传感器是根据两点法来求解导数,而磁场的衰减并非线性关系,因此十字形传感器实际求解的是B点的梯度张量矩阵,而对于永磁体来说,应该求解D点的梯度张量值。因此,采用十字形传感器模型对梯度张量矩阵进行测量必然在原理上就存在误差。

图2 误差分析图
如图3所示,为了减小这种在原理上的测量误差,下面打算将测量的基线进行移动,保持测量基线AC的长度不变,将测量点A和测量点C进行平移至测量点A1和测量点C1,此时十字形传感器实际测量的点为B1,相对于之前的测量点B来说,进行平移之后的测量点B1更加接近理论值D点。因此,该思路能够在一定程度上减小十字形传感器的测量误差。
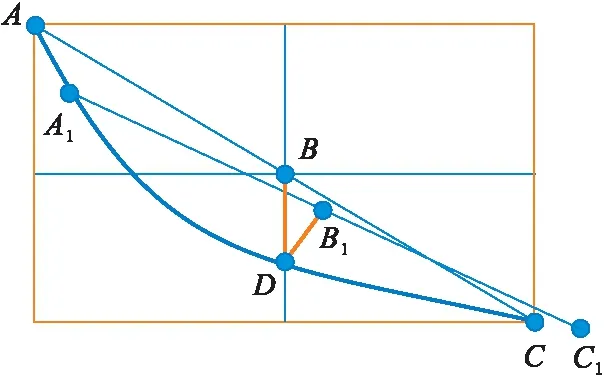
图3 解决思路图
2 免疫克隆算法优化
2.1 目标函数构建
在实际测量中,由于磁场的衰减与距离并非线性关系,而求解偏导数是基于磁场衰减规律是线性的基础上,因此梯度张量矩阵肯定存在误差,可以将梯度张量的实测值GT记为:
为了便于计算求解,假设以下这几个等式成立:
(11)
式中:rx+、ry+、rx-、ry-分别表示十字形磁力仪模型第1、2、3、4号磁力仪到永磁体的距离;x、y、z分别表示第0磁力仪在空间三维坐标系x、y、z轴上的坐标值;d表示十字形磁力仪模型中第1、2、3、4号磁力仪到第0磁力仪的距离;a、b分别表示实际测量时x轴上的第1、3磁力仪、y轴上的第2、4磁力仪的实际测量位置到以固定距离d建立的十字形磁力仪模型的第1、3磁力仪和第2、4磁力仪位置的距离偏差。
由于采用两点法求导必然存在误差,因此根据磁场的衰减规律,误差矩阵系数为:
(12)
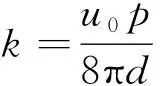
(13)
因此,目标函数可以表示为:
f=g1k1+g2k2+g3k3+g5k5+g6k6
(14)
式中:k1、k2、k3、k5和k6分别表示各自系数的权重。
2.2 算法实现流程
由于免疫克隆算法不受目标函数以及维数的限制,能够较好地解决优化问题,因此下面采用免疫克隆算法对目标函数进行优化求解。
具体求解步骤如下:
Step 1 目标函数的构建。
F(产品质量信用)=a1*f1(产品质量信用意愿)+a2*f2(产品质量提供能力)+a3*f3(产品质量保障能力)
确定问题的维数并根据磁场的衰减规律,构建梯度张量误差矩阵,设置目标函数为f。
Step 2 产生初始种群。
初始种群根据免疫维数、免疫个数以及免疫的上下门限来产生初始种群。
g=rand(D,n)*(r+-r-)+r-
(15)
Step 3 计算个体浓度和激励度。
个体浓度采用欧式距离进行计算,激励度根据相似度阈值来确定。
(16)
Step 4 免疫循环。
免疫循环阶段根据种群的亲和度,不断挑选亲和度最高的个体,并将亲和度最高的个体带入目标函数中进行计算。
亲和力计算公式为:
(17)
式中:tk是抗原和抗体k的结合强度。
Step 5 种群更新。
在不满足最优解的条件下,将新种群与旧种群进行合并并重新进入免疫循环阶段。
3 仿真计算
3.1 计算路线
为了验证免疫克隆算法优化的效果,设置了如图4所示的3条不同的路线。路线1保持z轴的坐标为0.4 m,x轴坐标与y轴坐标保持一定比值,路线2保持y轴的坐标为0.4 m,x轴坐标与z轴坐标保持一定比值,路线3保持x轴的坐标为0.4 m,y轴坐标与z轴坐标保持一定比值。因此,这3条路线能够代表整个空间的大体情况。在这3条不同的路线上,分别采用原始的一阶梯度张量和经过免疫克隆算法优化后的一阶梯度张量算法进行仿真定位实验。
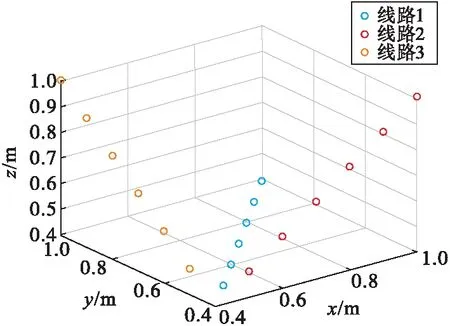
图4 测量路线分布图
3.2 定位精度
为了进一步比较定位效果,引入均方根误差进行对比分析:
(18)
对3条路线分别进行一阶梯度张量和经过免疫克隆算法优化的一阶梯度张量定位,不同路线的误差分布图如图5所示。
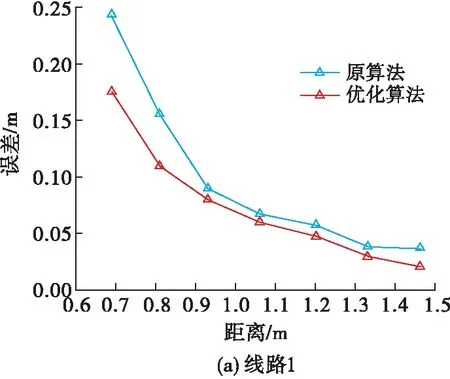
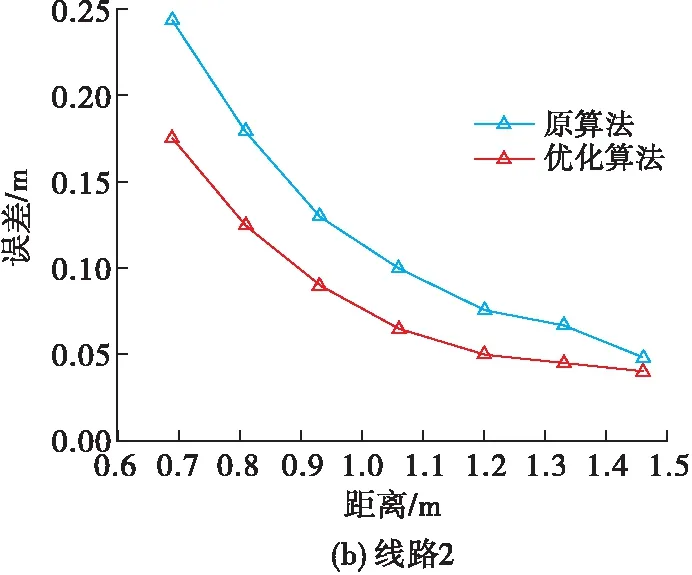
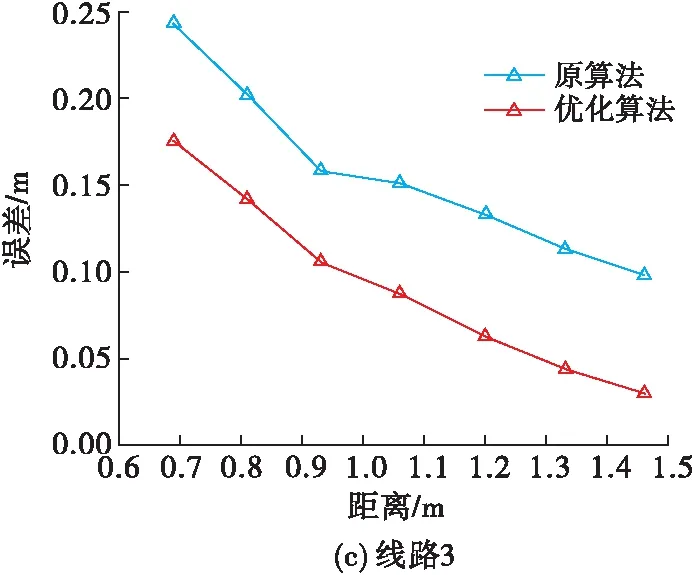
图5 不同路线的误差分布图
在图5的3个误差分布图中可得以下结论:在比较近的距离条件下,经过免疫克隆算法优化后的一阶梯度张量定位精度明显比原算法定位精度高。
4 实验验证
4.1 实验步骤
根据文献[2],当磁力仪与永磁体之间的距离大于永磁体尺径的10倍时,可以将永磁体视为磁偶极子分析。本实验使用长为9.6 cm、宽为4.7 cm、高为1.7 cm的长方体永磁体。将永磁体放置在距离测量阵列1 m以上的位置,由于磁力仪与永磁体之间的测量距离远大于永磁体的尺径,因此,可以将永磁体当做磁偶极子分析。具体实验步骤如下。
Step 1 安装设备。
首先,调整三脚架,使支架的气泡位于中间;然后,如图6所示,将5个磁力仪分别安装在固定位置并给设备加上24 V的电源。当数据采集模块的5个指示灯全亮时,说明磁力仪连接方式都对,设备可以正常工作。

图6 传感器模型
Step 2 放置永磁体。
如图7所示,将长方体永磁体固定放置在无磁转台的正中心上,设置无磁转台的旋转速率为4 rad/s,给设备通上24 V的电源,使其匀速旋转。当数据采集模块出现调制波形时,说明成功接收了永磁体的磁场。

图7 无磁转台
Step 3 数据采集。
设置数据采集的模式为连续采集,采集时间为10 s ,将10 s内采集的数据导入到文档中并且永磁体产生的磁场分布情况将会在磁场测量系统中显示出来。
Step 4 调整测量位置。
当上一个测量点的数据记录完毕时,调整十字形传感器的位置,将其放置在不同位置,继续重复数据采集模块的数据采集过程。
4.2 数据处理
当永磁体以固定速率匀速旋转10 s时,将会得到永磁体在这一阶段产生的永磁体的磁场分布如图8所示。
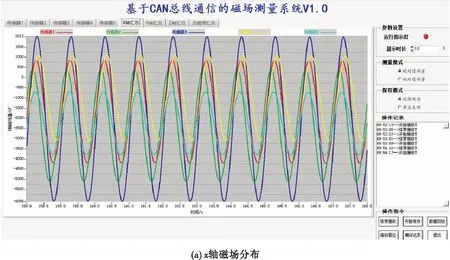
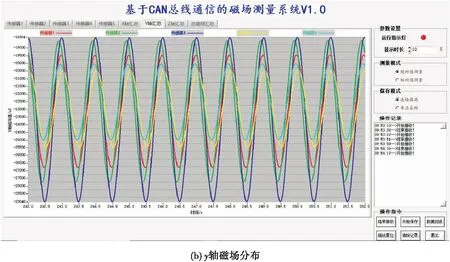
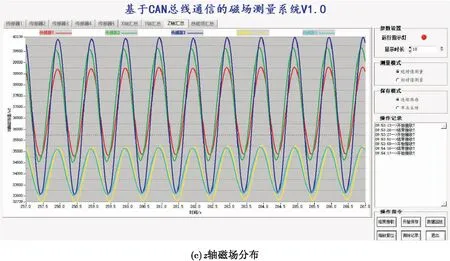
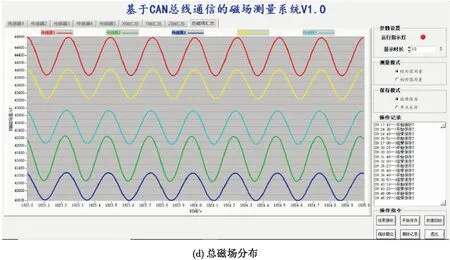
图8 旋转永磁体磁场分布
在图8中,所有波形图的横坐标表示时间,单位为秒。图8(a)的纵坐标表示x轴的磁场强度大小,图8(b)的纵坐标表示y轴的磁场强度大小,图8(c)的纵坐标表示z轴的磁场强度大小,图8(d)的纵坐标表示总磁场强度大小,所有单位都为纳特。当永磁体匀速旋转时,Bx、By、Bz、B都是调制信号,并且以一个固定信号波形周期性的重复出现。
尽管实验的环境处于一个较为空旷的地方,但是测量数据难免会受到地磁场和环境磁场的影响,因此,必须对数据进行滤波处理。
由于永磁体的旋转速率为4 r/s,因此滤波器的中心频率为4,通过滤波的方式,可以过滤掉地磁场和环境磁场,尽量减小外部环境对测量精度的影响。以传感器1为例,混有地磁场和环境磁场的原始数据见图9,通过滤波处理后的数据见图10。
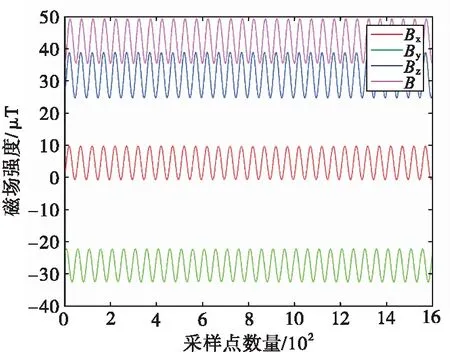
图9 原始数据分布图
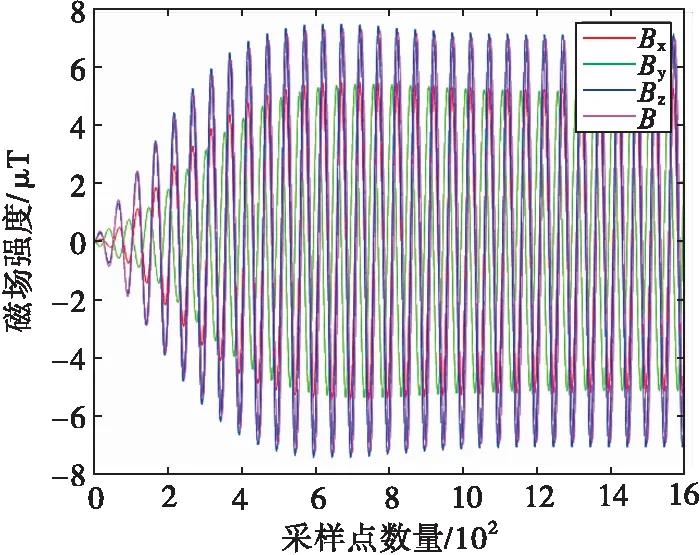
图10 永磁体数据分布图
在图9中,旋转永磁体产生的Bx、By、Bz、B都是类似于正弦波的调制信号,并且这种信号具有周期性。传感器2、3、4、5的永磁体磁场信号与传感器1的永磁体磁场信号的趋势与之类似。
在图10中,磁场强度的大小明显下降,说明通过滤波的方式,将静止的干扰磁场成功地滤掉。由于无磁转台刚开始需要一个加速的过程,因此在图10中,刚开始的磁场不是恒定的,当转台匀速旋转时,磁场慢慢趋于稳定。当采样点到600左右时,磁场信号逐渐趋向于稳定状态。当磁场信号稳定后,提取磁场信号在每一周期的最大值,将其视为测量值,分别代入到原始算法和优化算法中,得到测量点的相对误差。然后,继续在实验室随机取点,重复以上步骤,得到其他测量点的相对分布如表1所示。

表1 定位误差对比
从表1可以看出,在距离较近时,经过免疫克隆算法优化后的定位精度比原算法定位精度平均高5%左右,说明经过免疫克隆算法优化的定位效果略比原始算法的定位精度好。
5 结语
本文研究了免疫克隆算法在一阶梯度张量中的应用。在一阶梯度张量算法的基础上,提出了误差梯度张量矩阵并运用免疫克隆算法进行优化处理。在不同的路线上,将原算法和免疫克隆优化的定位算法进行对比分析并利用实际实验对优化算法进行实际验证。研究表明:在比较近的距离条件下,经过免疫克隆算法优化后的一阶梯度张量定位精度得到明显提高。
