星地认知网络中基于图论的动态频谱划分算法

朱圣铭， 杨霄鹏， 肖 楠， 刘东健， 徐志平

(1.空军工程大学信息与导航学院，西安，710077； 2.96862部队，河南洛阳，471000)

随着无线通信技术的快速发展和业务传输需求的不断增长，卫星通信与地面移动通信对频谱资源的竞争日益激烈，频谱资源紧缺导致的频谱拥塞和干扰问题逐渐成为制约卫星通信发展的主要因素之一[1]。虽然高频段卫星频率资源更加丰富，但有限的频谱资源始终是限制卫星卫星通信发展的重要因素[2]。为了提高无线频谱利用率，国内外学者先后提出了多种解决方案，如多载波频率复用、时空编码、多天线传输等，但这类技术采用的仍是静态分配策略，无法从根本上解决频谱资源分配不均衡与频率互干扰问题。认知无线电(cognitive radio，CR)[3]是实现频率高效利用的一种先进通信理论与技术。认知无线电在卫星通信中的应用能够提高空间频谱资源管理的灵活性，有效缓解频谱资源紧张和干扰问题，提高频谱资源的利用率。

由于图论模型在解决无线资源划分问题上方便有效，近些年来在地面通信网络中应用较多[4-6]。图论是数学中的一个重要分支，其利用点和边的集合描述研究对象之间的二元关系，由于其恰好与认知用户和授权用户之间频谱接入问题的解决思路相符合，近些年来受到广泛关注。采用图论解决频谱接入问题的思路就是通过对比认知用户通信参数(如对授权用户干扰功率或认知用户感知距离等)与设定值的大小，从而确定认知用户是否拥有接入授权频谱的权利。对于每个认知用户都有可供接入的授权用户集，通过对比相应的收益目标函数和多次迭代的方式来确定最佳的频谱接入方案。文献[7]在图论模型的基础上，加入认知用户功率矩阵和干扰阈值矩阵约束，量化了认知用户对授权用户的干扰和认知用户间的干扰，在此前提下，提升了认知系统整体的吞吐量。文献[8]将图论模型应用于多层频谱管理架构中，通过形成认知用户的感知态势图来获取对授权用户干扰及授权频谱可用性变化等信息，使得认知系统中的频谱接入过程更加清晰有效。文献[9]针对多授权用户情况，从可用授权信道数量、认知用户和授权用户部署密度及授权用户可同时接入的最大数量来描述认知用户与授权用户的连通性问题，其提出的模型架构可适用于大多数认知通信场景。而对于星地认知通信网络，其研究成果较少。图论模型具有较为直观的特性，利用其建立卫星认知通信网络拓补图，可使认知用户快速发现能够接入的授权用户频谱资源。

因此，本文将利用图论模型对多授权用户的卫星上行链路认知通信场景下的频谱划分问题开展研究，并将系统吞吐量作为评价认知用户接入授权用户时获得的收益指标，根据认知用户及其范围内的授权用户的通信参数构建能反映认知用户个体收益的目标函数，通过多次迭代确定在各认知用户效用函数达到最大的频谱接入矩阵，从而最大限度地满足用户业务需求。

1 系统模型及问题描述

以往许多学者的研究表明，在星地网络间进行卫星认知用户的动态频谱接入是可行的，多个认知用户可对单授权用户进行频谱接入。但在现实情况中，一定区域范围内的认知用户数量和授权用户数量通常为多个，这就大大增加了卫星认知用户进行动态频谱接入[10]的复杂程度。为了降低频谱接入的复杂度，需要将多认知用户对多授权用户进行频谱接入的场景划分为若干个多认知用户对单独授权用户进行频谱接入的场景，使问题模型得以简化。

简单的图论模型可表示为：

G=(V,E)

(1)

式中：(V,E)表示无向图G的一个二元组；V为图G的顶点集；E为图G中边的集合。

考虑到在卫星认知通信场景中存在认知用户和授权用户两方，并且需要设计合适的效用函数，以便对认知用户是否可以接入授权频谱的情况做出判断，则式(1)可表示为：

G=(V1,V2,E,U)

(2)

式中：V1= {vi|i= 1, 2,…,n}和V2= {vj|j= 1, 2,…,m}分别为卫星认知网络中的认知用户和授权用户；E为认知用户与其感知到的授权用户之间的连接关系；U表示当认知用户根据集合E选择一个授权用户进行接入其获得的收益集合。设L=lijn×m为图G的邻接矩阵，则：

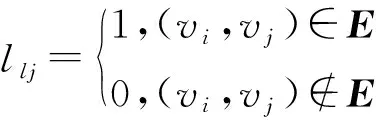
(3)

设U=uijn×m为图G中认知用户的收益矩阵，则：

(4)

式中：Uij表示在认知用户i可以感知到授权用户j的情况下，认知用户i对授权用户j进行频谱接入时获得的收益。

在星地网络间卫星认知通信场景中，多授权用户情况下的认知用户动态频谱接入如图1所示。

图1 多授权用户情况下的卫星认知通信场景

文献[11]提出的Generalized-K信道模型不仅符合卫星链路中信号的传输形式，而且还可以较好地描述地面链路的信号特征。图1中，认知用户与授权用户(下文称认知节点和授权节点)共存于同一通信场景。由于地面通信环境多径因素较多，所以其两者间的信道模型可用Generalized-K信道模型来表示。

在该模型中，视距分量和多径分量的幅度均服从Nakagami-m分布，则接收信号功率的概率密度函数为:

(5)

在Underlay模式[12]中，认知用户无需感知授权用户是否占用频谱，允许接入授权用户使用的频段，但是需要预先感知授权用户正常工作时所能容忍的最大干扰功率，从而严格控制自身传输功率，使得产生的干扰不超过此阈值，如图2所示。本文通过采用数据库技术(database technique)[13]建立干扰模型，通过该技术，认知卫星用户可以获得有关各种运行参数的信息，如信道数量、中心频率和该点可用的功率级别等。另一方面，认知用户在Underlay模式中也可以动态感知频谱是否被占用，若未被占用，可以加大功率使用频段；若授权用户再次使用，则需要重新调整功率避免超过干扰阈值。因此，在Underlay模式中，认知用户可以根据频谱感知状态来动态调整自身功率，使得收益最大化。

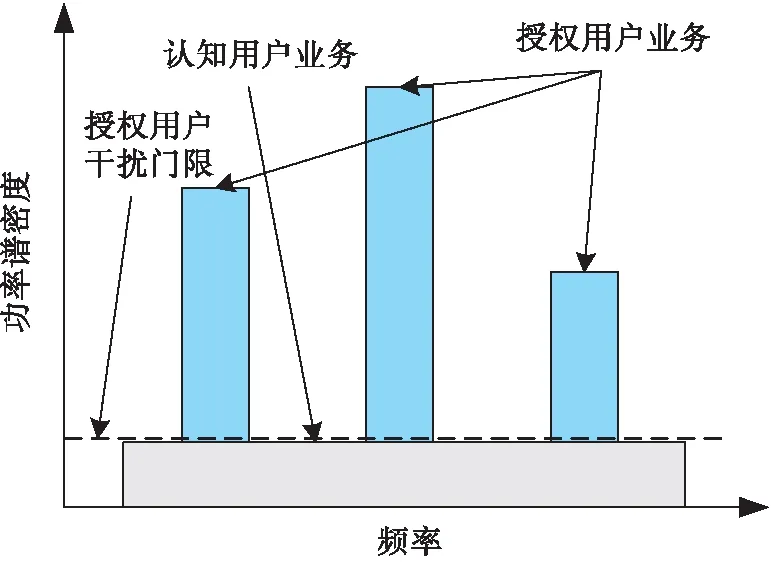
图2 Underlay模式下认知用户频谱接入示意图

在本文提出的假设中，对于同一认知用户i，可能存在多个授权用户频谱可其供接入，此时认知用户i需要选择使得自身获得收益Uij最大的授权用户进行频谱接入。而当其他认知用户也选择此授权用户时，会造成所有接入该授权频谱的认知用户获得的收益下降，此时对于认知用户i可接入的其他授权用户的频谱收益可能大于之前i所选择的授权用户频谱收益，认知用户i需要对其周围的授权用户进行重新选择。当经过多次迭代后，认知用户i的选择不再变化时，其被划分到收益最大的授权频谱中。

2 基于图论的动态频谱划分算法

图1所定义的场景中，将星地认知网络覆盖区域定义为G，则认知节点vi和授权节点vj可表示为：

vi=(xi,yi)

(6)

vj=(xj,yj)

(7)

式中：xi和yi、xj和yj，分别为认知节点vi和授权节点vj在图G中的横纵坐标，假设认知节点vi的感知范围为Di，根据式(6)、(7)，则有：

(8)

L=lijn×m为认知节点vi和授权节点vj间的频谱感知矩阵。当授权节点vj可以被认知节点vi检测到时，lij=1；当授权节点vj未在认知节点vi的感知范围内，该部分授权频谱不可被认知节点vi利用，所以lij=0。

假设授权节点之间无频谱重叠情况，认知节点仅对进行接入的授权节点产生干扰。根据式(4)，认知节点vi对授权节点vj进行频谱接入时获得的收益uij可表示为：

(9)

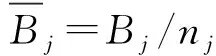
(10)

式中：Pij_int为认知节点vi对授权节点vj的干扰功率大小，考虑到授权节点vi频谱划分的公平性，对于各认知节点vi，Pij_int的最大值可表示为：

(11)

式中：Tj_th定义为授权节点vj的最大干扰温度，根据Generalized-K信道模型，在认知节点vi接入授权节点vj频谱的情况下，当使得uij最大时，Pi可表示为：

(12)

式中：hij为认知节点vi到授权节点vj的信道冲击响应，令gij=|hij|2，根据式(5)、(12)，Pi可表示为：

(13)

将式(13)代入式(9)中，可得：

(14)

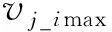
(15)

式中：Pi为认知节点vi所能感知到的所有授权节点的集合，令A=aijn×m为最佳接入矩阵，则A可表示为：

(16)

设迭代次数为c时的收益矩阵为U(c)，A(c)根据U(c)更新自身的元素值aij。当对于接入矩阵A经过c0次迭代仍不改变，即A(c-c0)=A(c-c0+1)=…=A(c)，则A(c)为最终的最佳接入矩阵。

根据上述内容，基于图论模型的频谱划分算法流程如图3所示。

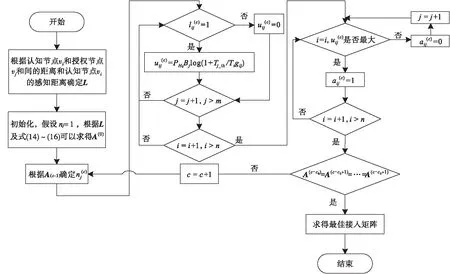
图3 基于图论模型的频谱划分算法流程

由上图可知，对于图G，首先要计算认知节点和授权节点间的感知矩阵L，其次进行参数的初始化，在不考虑接入授权节点vj认知节点数量的情况下，即nj=1，直接根据频谱收益大小来确定授权节点vj_imax(0)，其目的是得到最佳接入矩阵的初始值A(0)。然后进行授权节点vj的频谱划分，通过式(14) ～ (16)确定最佳接入矩阵，当迭代次数c达到条件时，停止迭代，求得最终的最佳接入矩阵A(c)。

3 仿真结果与分析

在本文研究的多授权节点卫星认知通信场景中，所有认知节点类型相同，所有授权节点也为同一类型。部分参数如表1所示。

表1 部分参数

其中，认知节点与授权节点在20 km × 20 km的区域内均匀分布。根据文献[14]，本文采用的Generalized-K信道模型有3种不同衰落程度的参数组合：①在轻度衰落模式中，mA=38.08,mZ=3；②在中度衰落模式中，mA=7.91,mZ=2.5；③在重度衰落模式中，mA=1.09,mZ=1.5。在本文仿真实验中，选取衰落模式为中度的Generalized-K信道模型，即mA与mZ分别为7.91和2.5。认知节点vi与授权节点vj的具体参数见表2和表3。

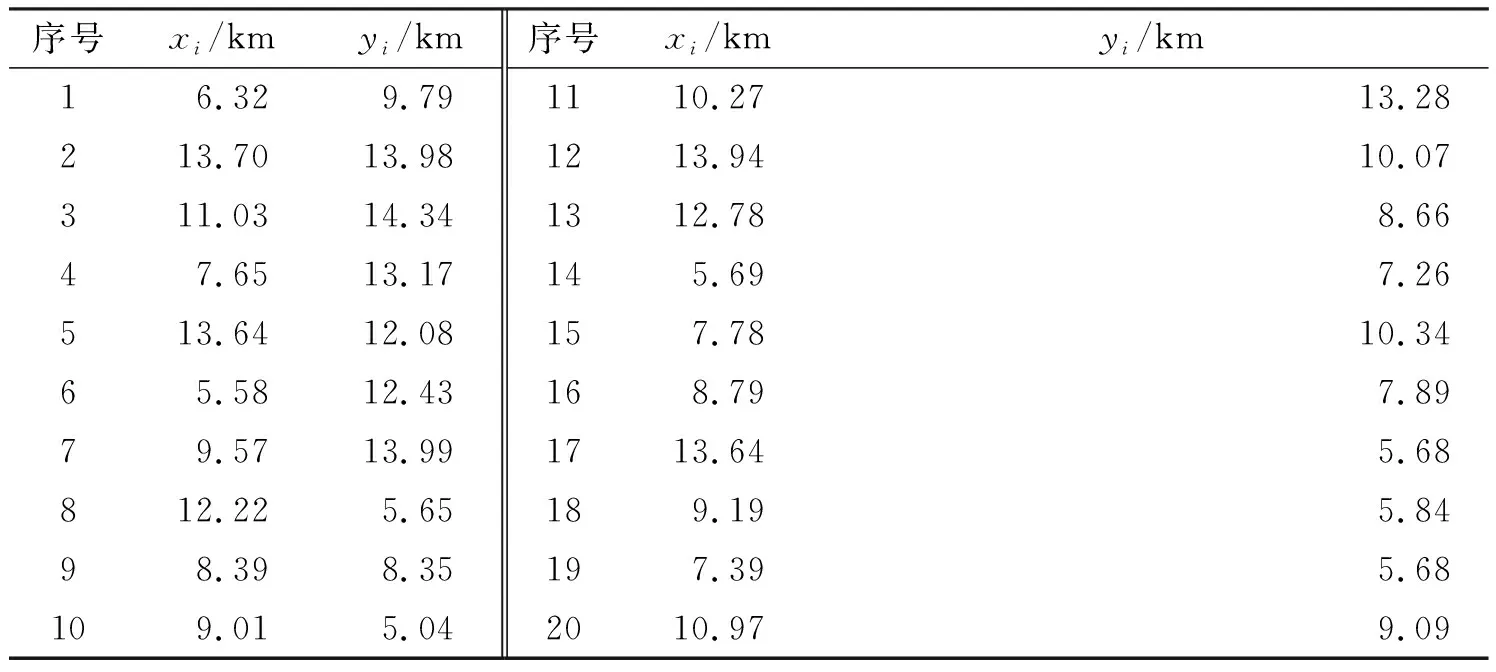
表2 认知节点的坐标参数

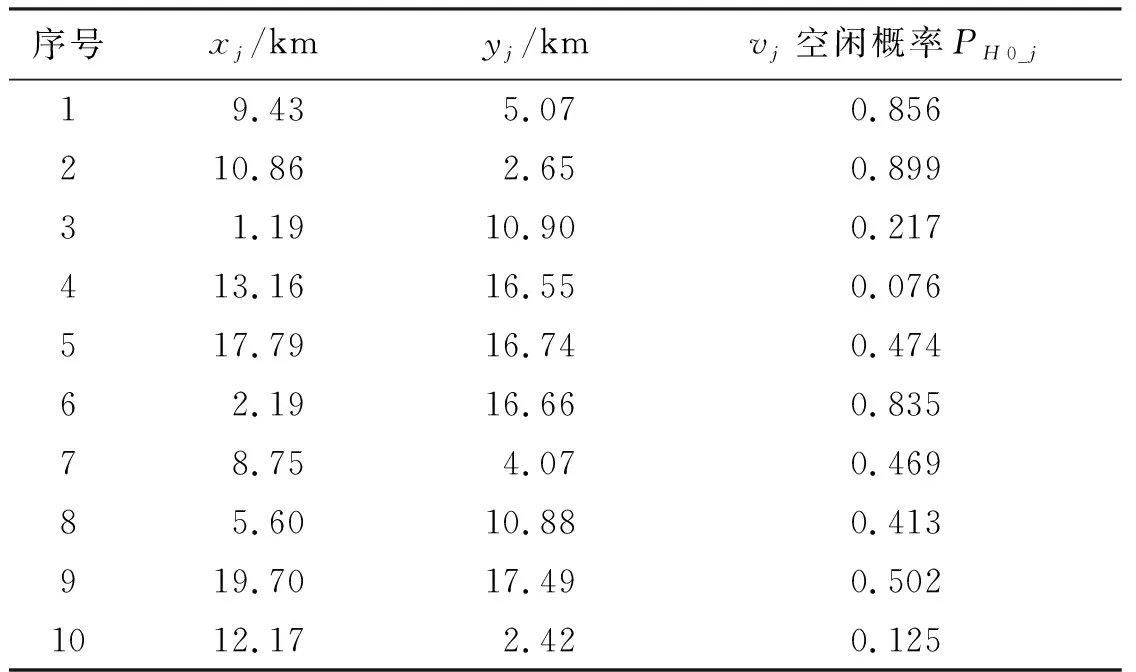
表3 授权节点的坐标参数及频谱空闲率

将认知节点vi表示为SUi，授权节点vj表示为PUj，根据以上参数，认知节点与授权节点的平面分布图如图3所示。

图3 认知节点与授权节点的平面分布图

上图中红色十字代表授权节点，蓝色方块代表认知节点，黑色虚线代表认知节点的感知范围。首先通过式(7)确定频谱感知矩阵，找到认知节点vi的可用接入链路，如图4所示。

图4 认知节点的可用接入链路

由图4可知，认知节点SU12的感知范围内没有授权节点，所以其不能进行频谱接入。而对于授权节点PU6和PU9，由于其不在任何一个认知节点的感知范围内，所以它们的频谱资源不能被利用。根据图4，需要确定初始的接入矩阵A(0)，通过计算，初始的认知节点接入链路可以在图4的基础上表现为图5。

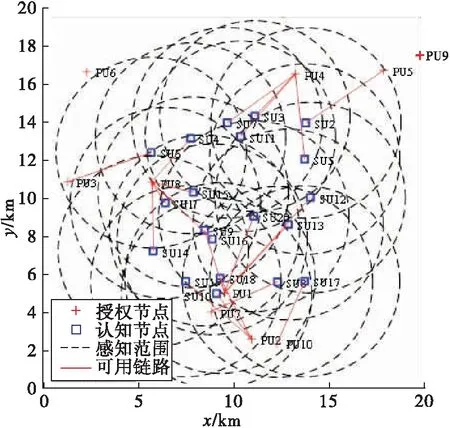
图5 初始时认知节点接入链路

根据迭代次数条件，设c0= 2，经过实验仿真，测得c= 11时，频谱划分达到最优，即A(9)=A(10)=A(11)。图5为不同迭代次数情况下的授权频谱划分平面图。

图6(a)、(b)分别为迭代次数为8和9时的授权频谱划分平面图，每条接入链路上显示了认知节点频谱收益uij的大小。在图6(b)中，认知节点SU18不接入与其距离较近的授权节点PU1和PU7，而是选择接入与其距离较远的PU2，这是因为当距离较近时，由于授权节点的干扰条件限制，认知节点要降低自身功率以避免对授权节点产生干扰，所以对于认知节点，会选择在自身感知范围内距离较远的授权节点进行接入，以提升自身的频谱收益。由图6(a)和图6(b)的对比可以看出，当迭代次数为8时，接入策略未达到最佳，认知节点SU14和SU16的频谱收益分别为1.182 5和0.524 72，当迭代次数达到9时，SU14和SU16的频谱收益提升为1.581 1和1.353 6，证明了该算法可以在提升认知节点频谱收益的同时，完成授权频谱的动态划分。

图6 不同迭代次数的授权频谱划分平面图

4 结语

本文针对星地网络间多授权用户的卫星认知通信场景展开研究，对于该场景中多授权用户频谱接入问题提出了基于图论模型的授权频谱划分方法。首先介绍了多授权用户情况下的卫星认知通信场景，其次利用图论对该场景下的授权频谱划分问题进行建模分析，将其划分为多个认知用户与单个授权用户进行频谱接入的场景，设计了授权频谱划分流程，实验结果表明，文中算法可在考虑授权用户干扰条件的情况下，兼顾认知用户频谱收益，完成网络中授权频谱的划分。