白萝卜种子颗粒模型离散元接触参数标定与试验

闫建伟， 魏松， 胡冬军， 刘启合， 张富贵

（贵州大学机械工程学院，现代制造技术教育部重点实验室，贵阳 550025）

白萝卜具有丰富的营养元素和应用价值，其产量和种植面积在近些年大幅度上升，传统的人力播种方式难以满足生产需要，推进白萝卜播种机械化迫在眉睫[1]。近年来，计算机技术与离散单元法（discrete element method，DEM）的快速发展为播种机械的设计及优化提供了有力的基础。DEM广泛用于仿真分析农业散体物料与装备机械间的相互作用关系，其对于农业工程未来的发展起着关键作用[2]。而农业物料颗粒作为农业机械播种装备的介质，其接触关系和动态响应特性直接影响农业装备工作性能[3-5]。因此，合理的种子颗粒仿真模型对于优化农业播种装备至关重要。当采用颗粒聚合方式建立颗粒离散元模型时，填充颗粒半径越小、数量越多就越能接近种子的真实形态，但会大规模增加离散元模拟的仿真量和仿真时间。

在应用DEM进行农业颗粒物料参数标定初期，直接选用EDEM软件中简单的球形颗粒代替颗粒物料。在实际问题中，多数农业物料颗粒形状不规则，用球形颗粒标定的参数进行仿真易造成失真。随着离散元单元理论和建模技术的快速发展，对小颗粒、形状不规则颗粒的建模得到不断健全和完善。王云霞等[6]用原颗粒聚合体的方法建立玉米种子仿真模型，得到3种不同形状的玉米离散元模型，标定后的玉米物性参数与所选用玉米品种真实的物理特性较为接近；于庆旭等[7]等用采用多球粘结模型建立了不同填充半颗粒半径的三七种子离散元模型；戴飞等[8]基于多球粘接原理建立不同亚麻脱粒物料脱粒过程中种子、叶片、茎秆和粉尘4种类型离散元模型，用于亚麻脱粒料分离清选过程模拟与试验。

为了节省计算时间，Zhang等[9]利用放大的水稻颗粒模型，采用虚拟试验设计方法对未脱壳水稻颗粒的休止角进行了预测，将大米颗粒的形状放大3倍，然后用7个大米颗粒与放大的大米颗粒相匹配的方法进行近似代替，在保证仿真精度前提下，节省了60%的计算时间；张荣芳等[10]借助三维扫描与逆向拟合方法获取水稻种子外形，通过多球粘结建立不同填充半径颗粒水稻离散元模型，并结合仿真和台架试验得出最佳水稻气固耦合仿真模型；Deshpande等[11]将离散元与计算流体力学模型相结合进行模拟，研究了不同颗粒半径颗粒球形度、空隙率和压降在各种流体条件下的复杂关系；Yang等[12]采用颗粒重叠法建立了不同半径煤粒仿真模型，以堆积密度、孔隙率及仿真与实际试验的误差为指标，得到了3种较为精确的接触模型和相互作用参数。

现有物料参数标定中颗粒模型的选择大多数选择既定的填充颗粒半径大小，并未分析仿真颗粒球形半径对仿真时间和精度的影响。仿真颗粒模型通过简单手动填充或者自动填充2种方式建立，前者仿真精度不高，容易出现失真问题；后者建立的仿真颗粒模型虽然精度比前者高，且得出的数据误差较小，但其选择填充半径不经过具体的讨论而直接采用，容易造成大量计算时间的浪费，且仿真相对精度提升效果不明显。本文针对不同填充半径白萝卜种子离散元进行接触参数标定，并结合仿真时间与仿真精度确定了白萝卜种子离散元仿真模型最佳颗粒填充半径，以期为其排种器设计和研究提供一定的参考。

1 材料与方法

1.1 堆积角测定

供试材料为先科沃达白玉2号白萝卜种子，由贵州大学农学院提供。经测量，白萝卜种子平均长度4.23 mm，平均宽度3.47 mm，平均厚度3.16 mm，含水率8%。选取3 000粒三轴尺寸在平均值附近的白萝卜种子进行堆积试验。物理堆积角实际测量装置为无盖有机玻璃盒，其长、宽、高均为50 mm，玻璃板厚度为3 mm；底板长、宽均为200 mm，玻璃板厚度3 mm。滑落堆积试验时，将白萝卜种子从有机玻璃盒上方放入，种子自然下落在装置中，当种堆静止不动时，向上抽出右侧挡板种子向开口滑落并堆积，待种群稳定时，形成的斜面与水平面即为堆积角，如图1所示。重复5次，利用数码相机将每次试验结果垂直于种堆坡度角进行拍摄。

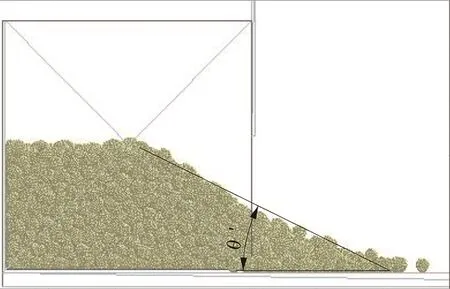
图1 测量装置Fig.1 Measurement device

1.2 仿真模型构建

1.2.1 轮廓模型 本文选取长、宽、厚与平均值相近的白萝卜种子建立其轮廓模型，白萝卜种子颗粒较小，故对选取的种子进行红蜡着色处理以便于扫描。白萝卜种子外形不规则，为了更为精确地建立轮廓模型，基于逆向工程理论，运用EinScan-3D扫描仪采用蓝光拍照式扫描白萝卜种子外轮廓，得到白萝卜种子的点云数据，将点云数据导入UG软件中转换为多边形，通过删除噪点、整体光顺、去除钉状物等优化处理得到白萝卜种子轮廓模型（图2），导出.stl格式的白萝卜种子颗粒轮廓模型文件。

图2 白萝卜种子轮廓模型Fig.2 Radish seed contour model

1.2.2 离散元模型 将UG软件导出的格式为.stl的白萝卜种子三维模型作为几何体导入到EDEM2019软件中，选择白萝卜种子内部上端为颗粒生成工厂，球形颗粒接触模型为Hertz-Mindin无滑移模型，为使球形颗粒填充效果好，设定较小的碰撞恢复系数、动静摩擦系数和较大的重力加速度。采用不同的填充球形颗粒半径范围0.10～0.35 mm，步长0.05；待球颗粒填充满白萝卜种子模型后，在EDEM后处理界面中导出所有球颗粒坐标数据（球形颗粒半径、编号和中心坐标）并对坐标数据进行处理。将仿真时间归零，导出.xml格式的文件，将坐标数据插入到dec文件中，在新建的EDEM文件particle项中导入此dec文件后，EDEM软件会自动生成白萝卜种子粒模型。最终得到不同填充数目的白萝卜种子离散元模型。

1.3 显著性参数确定方法

Plackett-Burman试验是基于目标响应与各因素之间的关系，比较各个因素2水平间的差异来确定因素显著性[13]。为准确寻找仿真参数中具有显著效应的参数及范围，本文以填充半径为0.3 mm的白萝卜种子模型为例进行Plackett-Burman试验，以白萝卜种子堆积角为响应值，对仿真接触参数的显著性进行筛选。

基于已有研究进展[14-18]和大量预试验，确定本文采用的仿真参数设置，如表1所示。

表1 仿真试验参数Table 1 Parameter in simulation experiment

以Design-Expert软件进行Plackett-Burman试验设计，对仿真接触参数进行筛选，仿真试验参数水平如表2所示。

表2 Plackett-Burman试验参数Table 2 Parameter of Plackett-Burman test

1.4 显著接触参数标定方法

本研究结合文献[14]和预试验取值（白萝卜种子-有机玻璃恢复系数0.4、白萝卜种子-有机玻璃滚动摩擦因数0.007、白萝卜种子-有机玻璃恢复因数0.2和白萝卜种子-白萝卜种子滚动摩擦因数0.01）进行参数标定。应用Design-Expert软件设计Box-Behnken试验，通过响应面建立二次回归模型对堆积角寻求最优解。以x2（白萝卜种子-有机玻璃静摩擦因数）、x5（白萝卜种子-白萝卜种子静摩擦因数）为试验因素，堆积角θ为试验指标。堆体仿真试验因素的水平如表3所示。

表3 Box-Behnken试验因素编码Table 3 Factors and codes of Box-Behnken test

1.5 验证评价

将不同填充半径颗粒半径的白萝卜种子离散元模型标定后的接触参数带入EDEM软件中分别对进行堆积角仿真试验，每组堆积试验重复5次，取其平均值，同时记录每组仿真堆积角试验所用的实际时间。并计算与实际堆积角27.88°相对比计算其相对误差率，如式（3）所示。

式中，θ′为堆积角仿真值，（°）；,θ为堆积角实测值，（°）。

2 结果与分析

2.1 白萝卜模型填充效果分析

结合图3和表4可知，填充球半径越小，其所需颗粒越多；当填充半径大于0.3 mm时，其颗粒数量相对稳定，当颗粒填充半径越小时，其填充数量差异较大。图4为不同填充球半径的白萝卜离散元模型，可以看出，填充半径越小，白萝卜种子的颗粒模型图与实物的外形更为相似。

图3 不同半径球形颗粒填充的白萝卜种子模型Fig.3 Radish seed model filled with spherical particles with different radius

图4 不同填充球半径的白萝卜种子离散元模型Fig.4 Discrete element model of radish with different radius of filling ball

表4 白萝卜种子仿真模型对应填充球半径与数量Table 4 Radius and quantity of filling balls corresponding to white radish seed simulation model

2.2 堆积角的实验测定结果

堆积角测定中所采集的图像及其处理结果如图5所示。可以看出，堆积轮廓拟合曲线与堆积轮廓重合度理想，说明堆积角设计合理。形成的堆积角如表5所示，堆积角的平均值27.88°，极差1.86°，标准差为0.669 0°。可知，形成的堆积角差异不大，因此，该结果可以用于仿真试验时白萝卜种子颗粒模型接触参数标定的目标值。

图5 堆积角图像处理Fig.5 Image processing of natural stacking angle in experiment

2.3 堆积角的仿真结果分析

从表5可以看出，实际堆积实验测定的堆积角平均值27.88°已包含在仿真模拟实验结果中，这表明试验因素水平选取合理。并且第3组试验结果与实际堆积试验结果最为接近，表明该组试验的参数最接近所求参数。图像处理结果如图6所示，可见，堆积角轮廓拟合线与实际轮廓边缘重合较多，说明仿真处理结果能够真实反应堆积轮廓。

图6 模拟堆积角图像处理Fig.6 Image processing of response angle in simulation

表5 堆积角测量结果Table 5 Measurement results of natural stacking angle

2.4 Plackett-Burman试验结果分析

利用Design-Expert软件对表6结果进行方差分析，得到各参数显著性如表7所示。由表7可知，白萝卜种子-白萝卜种子静摩擦因数和白萝卜种子-有机玻璃静摩擦因数对颗粒堆积角影响极其显著；白萝卜种子-白萝卜种子碰撞系数对颗粒堆积角影响较为显著；白萝卜种子-有机玻璃滚动摩擦因数、白萝卜种子-有机玻璃恢复系数对颗粒堆积角影响极小。

表6 Plackett-Burman试验设计及结果Table 6 Design and results of Plackett-Burman test

表7 参数显著性分析Table 7 Analysis of parameters of significance

2.5 Box-Behnken试验设计及结果分析

按照表8中所设定的仿真参数模拟堆积试验，共进行17组试验，试验方案与结果如表8所示。可以看出，目标堆积角27.88°也包含在仿真模拟实验结果中，这表明Box-Behnken试验因素水平选取合理。同时由表中数据可知堆积角会随着白萝卜种子-有机玻璃静摩擦系数x2，白萝卜种子-白萝卜种子静摩擦系数x5的增大而增大。进一步说明得到的显著性参数结论合理有效。

表8 Box-Behnken试验设计及结果Table 8 Design and results of Box-Behnken test

利用Design-Expert软件对仿真试验结果进行方差分析，可得堆积角θ的回归模型如下。

Box-Behnken试验模型方差分析结果如表9所示，拟合回归模P＜0.000 1，说明堆积角与回归方程模型拟合度极显著；其中白萝卜种子-有机玻璃静摩擦系数（x2）和白萝卜种子-白萝卜种子静摩擦系数（x5）的P值均小于0.01，说明参数x2、x5对堆积角影响极其显著；决定系数R2（0.963 1）和校正决定系数R2Adj（0.946 4）均接近1，说明模型与实际试验拟合良好，说明试验合理有效；失拟项P＞0.05，说明不存在其他影响指标的主要因素存在；变异系数为1.60%，表明试验可靠性较高；试验精度AP=27.971，说明模型具有较高的精确度。

表9 Box-Behnken二次回归模型方差分析Table 9 Anova of modified model of Box-Behnken

利用Design-Expert软件的优化模块，以实际堆积角27.88°为目标，对模型进行最优解化求解。目标及约束方程如下。

由此，得到优化结果为白萝卜种子-有机玻璃静摩擦因数为0.53，白萝卜种子-白萝卜种子静摩擦因数为0.39。按照上述方法，分别对其他5种不同填充半径颗粒的白萝卜离散元模型进行白萝卜种子-有机玻璃静摩擦因数和白萝卜种子间静摩擦因数标定，标定结果如表10所示。可以看出，当不同填充半径颗粒半径的白萝卜离散元模型，其仿真试验得出的参数结果存在显著差异，当填充半径大于0.3 mm时，白萝卜种子-白萝卜种子间静摩擦因数变化较大，说明该条件下仿真精度明显下降，也进一步验证上文参数标定结果，即白萝卜种子-白萝卜种子对白萝卜种子物料特性的影响最大。

表10 不同填充半径白萝卜种子离散元模型标定接触参数结果Table 10 Calibration of contact parameters of radish with different filling radius using discrete element model

2.6 验证结果分析

将标定后的不同填充半径颗粒的白萝卜种子离散元模型的接触参数带入EDEM软件进行堆积试验，其结果如表11所示。可以看出，当颗粒填充半径越大，其仿真计算时间越短，但是仿真相对误差率增加；颗粒填充半径越小，其仿真相对误差率越小，但其仿真计算时间越长。当颗粒填充半径大于0.25 mm时，仿真相对误差变化较大，当颗粒半径大于0.20 mm时，仿真时间相对稳定，变化较小。故综合仿真时间与精度，颗粒填充半径最佳为0.25 mm时，其填充颗粒球半径最佳。

表11 不同填充半径颗粒离散元模型仿真与真实试验结果Table 11 Simulation and real test results of particle discrete element model with different filling radius

3 讨论

当采用多球粘接建立离散元仿真模型时，球形颗粒直径越小越接近种子实际轮廓，仿真精度越高，但球形颗粒的数量越多，仿真时间越长，易造成资源浪费等问题。现有物料参数标定的研究中，很少分析所建立模型的合理性和说明模型的选择依据。针对先科沃达白玉2号白萝卜种子，采用Plackett-Burman试验筛选出对白萝卜种堆积角影响极其显著的因素为白萝卜种种子-有机玻璃静摩擦因数、白萝卜种子间静摩擦因数。依据Box-Behnken试验，建立并优化2个极显著参数与堆积角间的二次回归模型，以实际堆积角为目标，对回归方程进行最优求解，得到不同填充半径颗粒的白萝卜种子-有机玻璃静摩擦因数以白萝卜种子间静摩擦因数。结合仿真时间和仿真精度得到白萝卜种最佳填充半径为0.25 mm，其仿真时间耗时较低且仿真精度较高。但是，需要指出的是，由于白萝卜种子品种繁多、颗粒形状极不规则，物理性质分布较宽，因此，若对比试验结果误差数据存在出入，需对白萝卜种子模型间参数重新标定。