大数据背景下无车承运人平台线路定价元素分析

王 威，施云天，吴晶晶

（1. 南通理工学院，江苏 南通 226002；2. 南京审计大学 金审学院，江苏 南京 210023）

1 背景及问题起源

科技的快速发展，物流运输的迅速展开，需要通过不同手段拓展业务，无车承运人业务迅速得到业界的认可各类研究很多并获得一些理论成果。目前，我国无车承运业发展的很快，将成为物流业的一种新模式，但无车承运人业务的快速发展带来了许多问题，如何科学地制定线路价格是亟待解决的问题。可以借鉴铁路线路收费标准，海运航线收费标准，以及货物运输的调度、其他关于科学定价的研究和目前比较关心的热点问题，优化运输等研究成果。本文以无车承运人的视角，参考已有的研究成果，对无车承运人的科学制定线路价格进行进一步的研究，以其促进无车承运人业务的发展，本文拟解决以下问题：（1） 通过定量分析研究影响无车承运人平台货运线路报价的主导因素；（2） 基于数据给出三次报价以及成本定价的模型。

2 模型假设

（1） 假设车型固定无拼载任务；（2） 假设不考虑货主报价的情况；（3） 假设市场价格及政策稳定；（4） 假设运输时间为起始时间减去到达时间。

3 符号说明

文中用到的符号及其说明如表1 所示。

表1 符号说明

4 货运线路定价主要因素

主要因素决定了无车承运人平台货运路线定价。针对此问题采用主成分分析的方法，利用SPSS 进行主成分分析，以确定各影响因素的权重。

本文对给出的数据，进行异常数据的清理，选取恰当的数据，并且将少量缺失数据补充完整。再对各影响变量进行无量纲化处理，例如业务类型、是否续签等变量，以得到筛选后的变量值，量化后的结果如表2 所示。

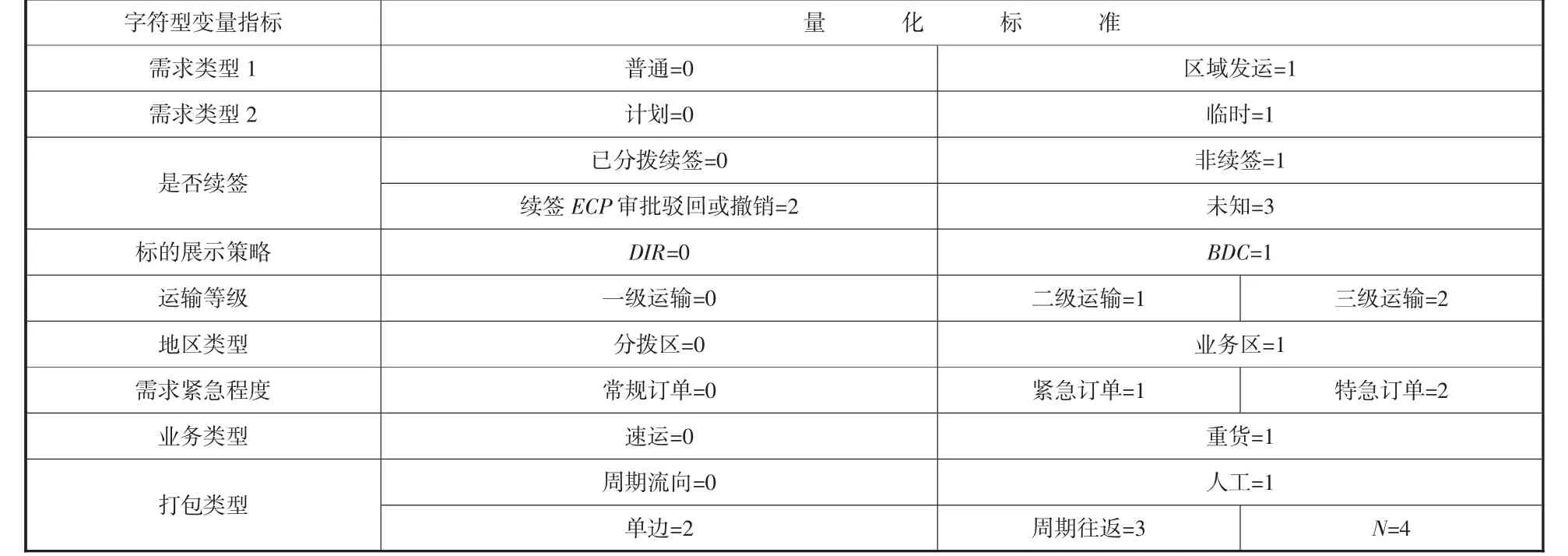
表2 变量量化结果

选取的变量如表2 所示，所选取的17 个变量都具有一定的代表性，此外还包括运输的里程总数、始发网点、目标网点、车辆长度及容量、线路编号以及运输时长等指标。之后对各个因素进行主成分分析，量化各个因素对货运线路定价的影响。

主成分分析是利用降维的基本思想，将N 维的成分因子经过正交变换，得到一组相互独立的K 维数据，以求获得主成分以及其相应的权重。具体分析过程如下：

将线路的定价作为研究对象，假设有A 个定价体系，有B 个因素的原始样本，构造矩阵X，表达式如下：

从表3 中可以看出，KMO>0.5 且P (Ba rtllet t )<0.1。结合这两个指标可以说明选取变量因素之间存在相关性，作进一步的因子分析，因子分析结果如表4 所示。

表3 KMO 和Bartlett 的检验

从表4 中可以看出有四个主成分的初始特征值大于1，且方差百分比大于70%。由此可确定用这四个主成分来代替原来预定的17 个影响因素，达到了很好的降维效果。

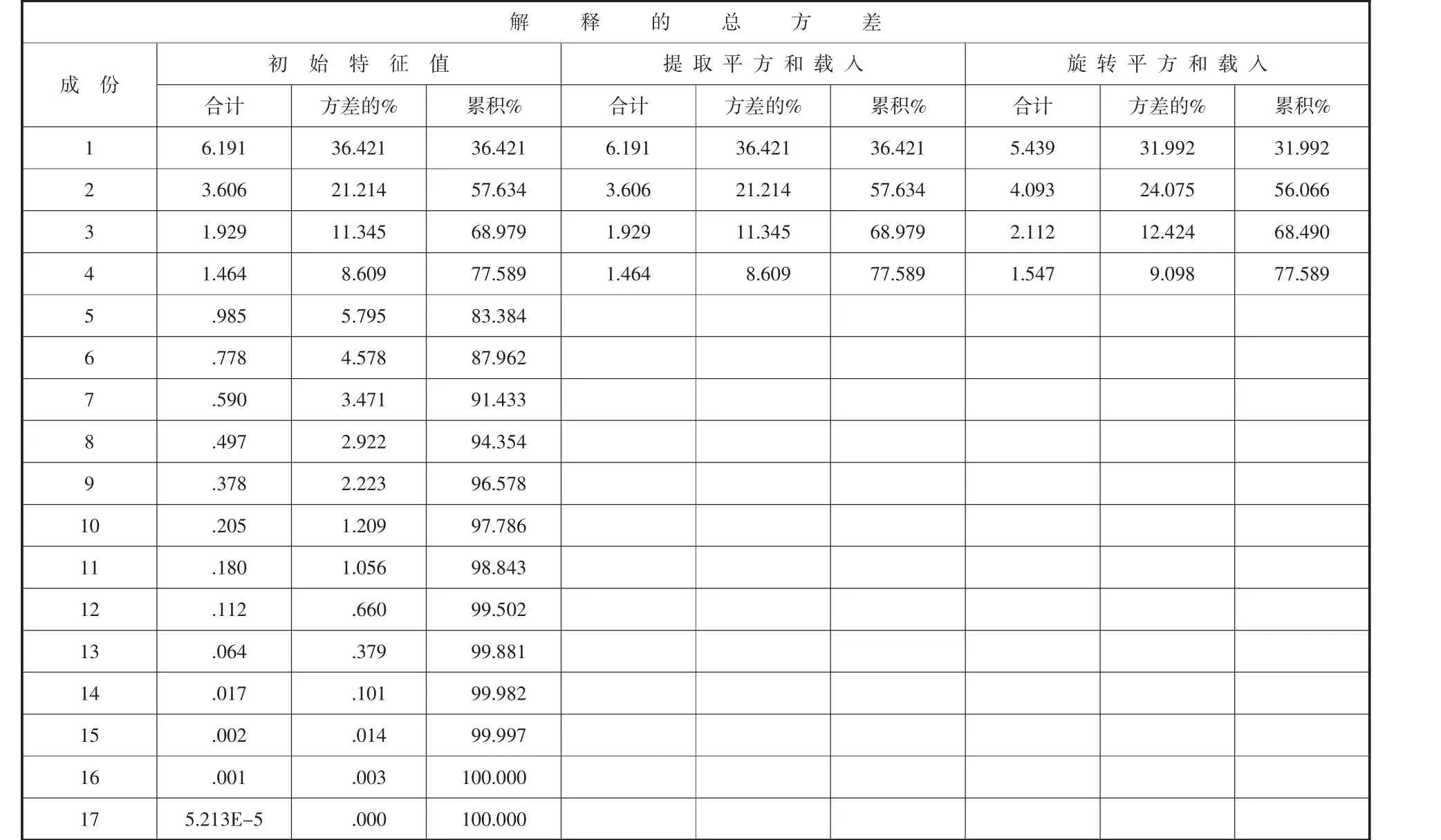
表4 因子分析

图1 碎石图含义为，其特征值标志为纵轴，成分表示为横轴。从图中可以看出前部分陡峭，特征值大，包含信息多。后部分平摊且特征值小，包含信息也较少。直观地看出主成分1、2、3、4 都包含了大量的信息，从主成分5 开始信息含量就减少了。更加说明由4 个因素代替原先的17 个因素是可行的。成分矩阵如表5 所示。

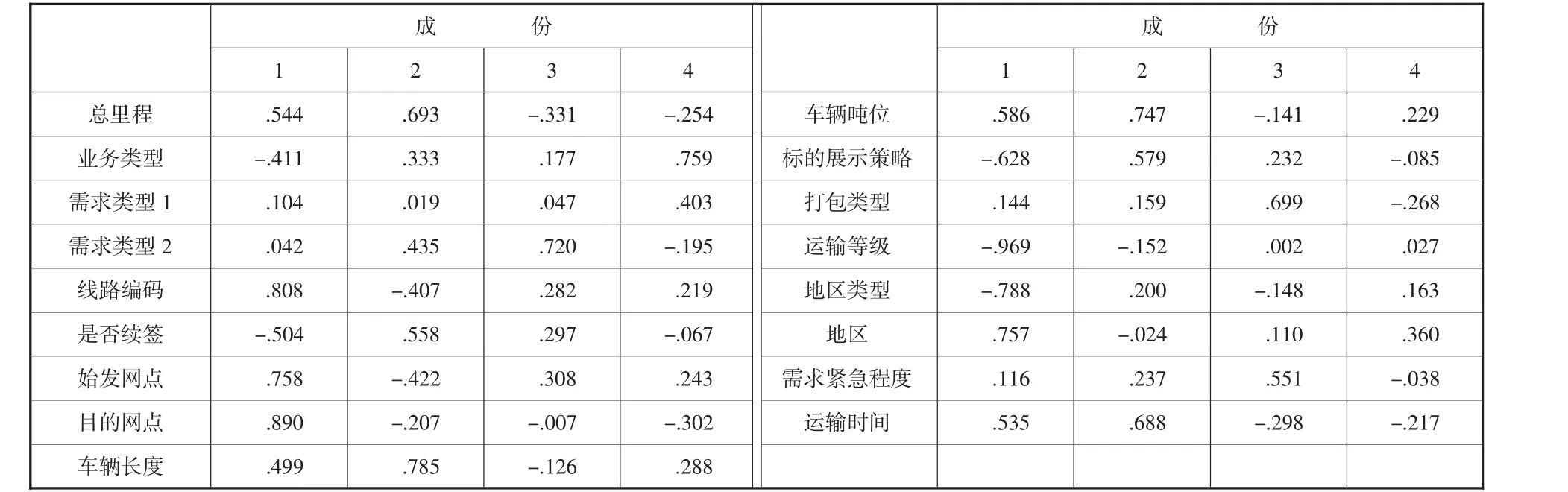
表5 成份矩阵

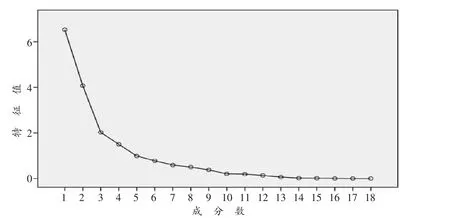
图1 碎石图

根据SPSS 主成分分析的结果，选取上面两表中的数据，并且对其指标的总权重W 进行求解。具体过程如下：

其中：k为主成分在组合中的权重，c为各个指标的值，m为第x 个主成分的值。

再确定每个主成分因素在综合模型中的系数值，利用初始特征值的方差百分比对各个主成分进行加权平均，得到：W

求得的权重系数如表6 所示。

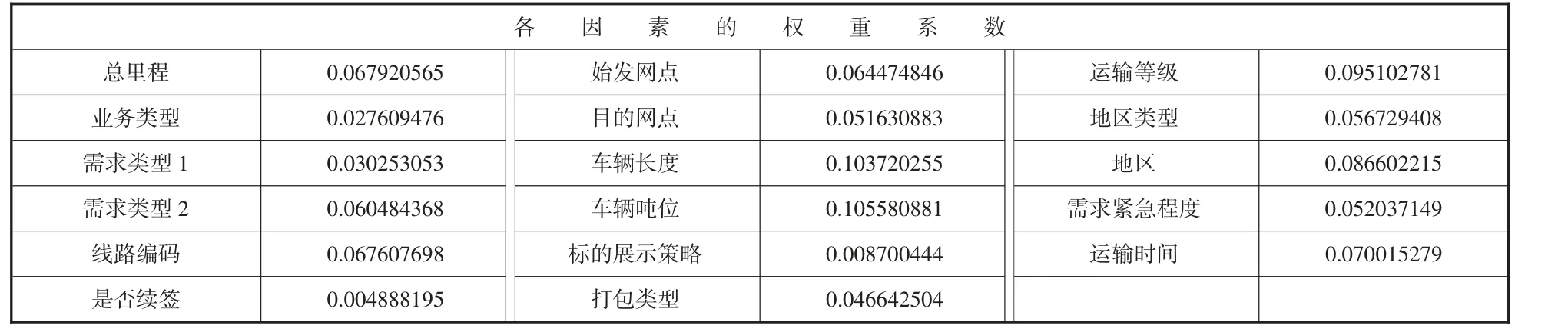
表6 各个因素的权重系数统计表

通过表6 可知，对无车承运人平台线路定价影响最大的因素为车辆的长度和承运车辆的吨位，两者的权重均大于0.1。而运输等级、时间、总里程数、位置以及路线编号和始发网点等因素的权重都在0.06 以上，影响程度相对较大。剩下的几个指标影响程度较小，大多小于0.05。

5 调价策略及评价

结合数据，建立多元回归模型探究影响定价的因素。并得到一次定价、线路成本以及三次定价的函数表达式，并进行了相应的求解。

将模型中概率值小于0.05 的即相关性最强的带入，而概率大于0.1 的从模型中剔除。

表7 模型汇总

R 方拟合度更优。

从表8 中可以看出模型一的回归平方和为214.311，残差平方和为210.079。并且总平方和=回归平方和+残差平方和。由于“回归平方和”跟“残差平方和”几乎接近，所以，此线性回归模型只解释了总平方和的一半。

表8 Anoval 分析

根据P（F 统计量）=0 可知，随着变量引入，其概率值均远小于0.01。仍需要进一步分析线性关系的强弱。

根据表9 已剔除变量表可知，第三次定价中车辆吨位T 检概率大于0.05，需要剔除。

表9 已剔除变量

回归方程的系数如表10 所示，由此可知，无车承运人平台中第一次、第三次定价以及成本价格的回归模型为：

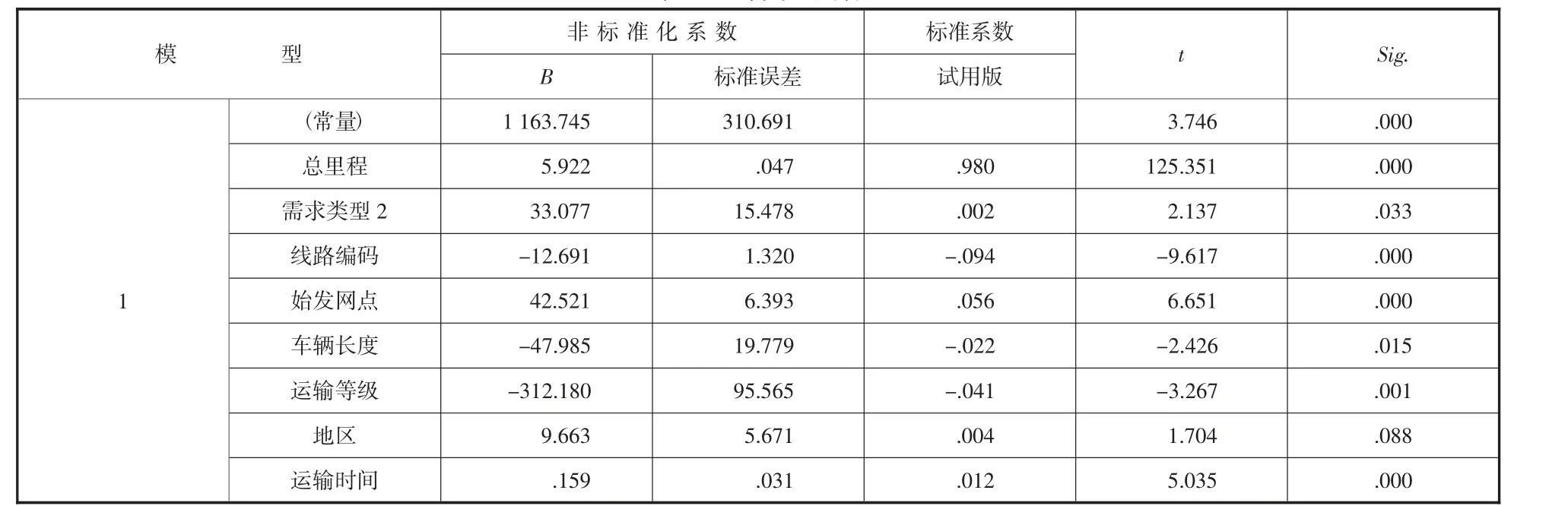
表10 方程系数

每条线路最多可以发布三次价格，即进行两次调价。将得到的上述三个回归表达式。

6 灵敏度分析

将本文所建模型中的输入变量都相应减少1%，观察其建模结果变化。通过分析可知，当所有影响因素都减小1%时，输出结果相应减小为1.02%、0.95%和1.01%。由此可见所建立模型的敏感性较好。

7 模型的不足

在主成分分析的过程中，难以准确知道每个主成分所表示的含义。无车承运人平台定价模型求解的结果仅仅反映了影响因素之间的内部联系，难以反映与最优解之间的关系。再进行多元回归时自动排除了某些变量，使得某些影响因子的影响程度难以预测。