判断函数奇偶性常出现的错误以及规避的措施
2022-07-13王颖
王颖

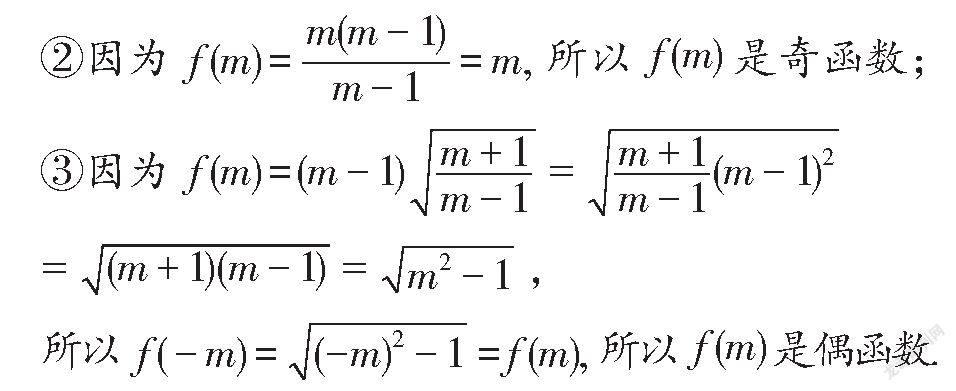
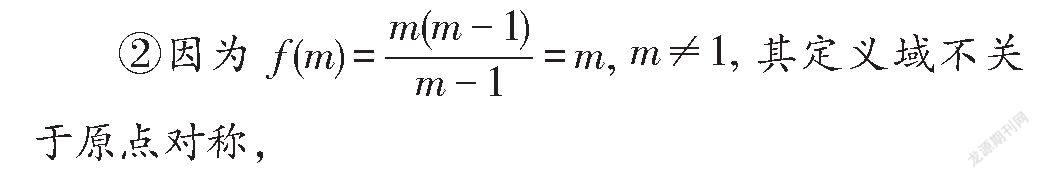
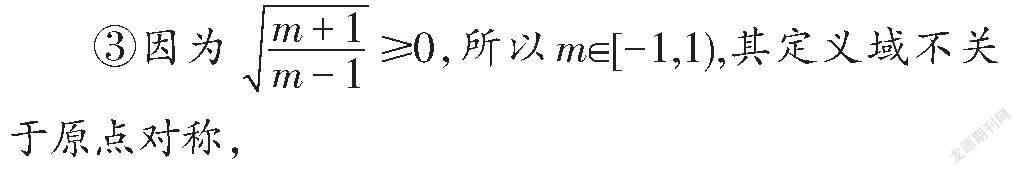

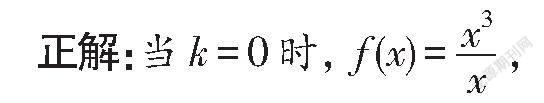

函数奇偶性是函数至关重要的性质之一.在判断函数的奇偶性时,很多同学经常出现各种错误.对此,笔者就同学们在判断函数奇偶性时常出现的错误进行了分析,并提出一些规避的措施,以期同学们能够从中吸取教训,避免重蹈覆辙.
错误之一:忽略了函数的定义域
函數的定义域是函数的三大要素之一,即函数自变量的取值范围.在判断函数的奇偶性时,很多同学常常忽略函数的定义域,致使解题出错.
所以f(m)为偶函数;
上述解法之所以错误,是因为忽略了函数的定义域.事实上,具有奇偶性的函数的定义域都关于原点对称,因此判断函数的奇偶性,需先要判断该函数的定义域是否关于原点对称.
正解:①因为函数f(m)的定义域为{-1,1}其关于原点对称,
又f(-x)=±f(x),所以该函数既是奇函数,又是偶函数;
所以f(m)既不是奇函数,也不是偶函数
所以f(m)既不是奇函数,也不是偶函数.
函数的定义域关于原点对称是一个函数具有奇偶性的前提条件,所以在判断函数的奇偶性时,同学们要高度重视函数的定义域,首先弄清楚函数的定义域是否关于原点对称,若不关于原点对称,则该函数不具有奇偶性.
错误之二:忽略了对参数的分类讨论
在判断含参函数的奇偶性时,需要对参数进行分类讨论.然而受习惯性思维的影响,许多同学经常容易忽略对参数的分类讨论,出现思虑不周的情况,致使求得的答案不完整,故而产生了错解.
错解:因为函数f(x)的定义域是(-∞,k)∪(k,+∞),其不关于原点对称,所以函数f(x)既不是奇函数,也不是偶函数.
上述错解产生的原因主要是受思维定式的影响,以为函数f(x)的定义域不关于原点对称,故而没有对参数k进行分类讨论,导致解题出错.事实上,当k=0时,该函数具有奇偶性.
该函数的定义域为(-∞,0)∪(0,+∞),
所以函数f(x)为偶函数;
当k≠0时,函数f(x)的定义域是(-∞,k)∪(k,+∞),其不关于原点对称,
所以函数f(x)既不是奇函数,也不是偶函数.
在做题时,同学们要克服思维定式的影响,全面考虑问题,对可能出现的情况作全面分析,尤其要重视对参数的分类讨论,从而做到不重复不遗漏任何情况,增加解答过程的完整性和准确性.在对参数进行分类讨论时,可将实数R看作全集,根据函数的定义域或函数式有意义确定分类讨论的分界线,将实数集划分为几个区间段,逐个进行讨论,最后综合所得的结果.
在判断函数的奇偶性时,同学们务必要沉着冷静,仔细审题,抓住函数式的特征,明确函数的定义域和参数对函数奇偶性的影响,根据函数奇偶性的定义进行判断.同时要养成检查和验算的良好习惯,及时发现和纠正错误,从而确保解题无误.
