一个组合几何命题的重新证明
2022-07-12吴波
吴 波
(1.重庆市八中两江金溪中学校 401120;2.重庆市长寿龙溪中学 401249)
1 一个几何定理溯源
文献[1]证明了杨路教授提出的如下问题:
定理1一个平面凸四边形,经过其中三个顶点可作一个圆,这样可得到4个圆(不排除其中有重合).如果这4个圆中有3个是等圆,则此4顶点共圆.
文献[1]对定理1的纯几何证明略显复杂.其实定理1当是源自于一个漂亮的几何恒等式.而这个几何恒等式也是杨路教授得到的,并收录在文献[2]中,即是:
定理2[2]平面凸四边形A1A2A3A4中|AiAj|=aij(1≤i (R1R2+R3R4)a12a34+(R1R4+R2R3)a14a23=(R1R3+R2R4)a13a24. 定理1的证明因四个外接圆中有3个是等圆,不妨设R1=R2=R3=R,代入定理2的恒等式可知三项的系数均为R(R+R4).约去R(R+R4)可得 a12a34+a14a23=a13a24, 由Ptolemy定理之逆即知定理1成立.证毕. 需要说明的是同,如果定理1中的平面四边形不是凸四边形,那么即便题设中那4个圆全是等圆,也不能保证四顶点共圆.事实上,存在这样的反例——当平面上四点A1,A2,A3,A4构成一个垂心组时,△A2A3A4,△A1A3A4,△A1A2A4,△A1A2A3的外接圆是等圆,但此四点显然不共圆. 文献[1]还将定理1推广到了平面凸五边形,平面凸六边形中,即(表述形式略有改动): 命题1[1]一个平面凸五边形,经过其中三个顶点可作一个圆,这样可得到10个圆(不排除其中有重合).如果这10个圆中(至少)有7个是等圆,则此5顶点共圆. 命题2[1]一个平面凸六边形,经过其中三个顶点可作一个圆,这样可得到20个圆(不排除其中有重合).如果这20个圆中(至少)有13个是等圆,则此6顶点共圆. 文献[1]用数学归纳法将其推广到了一般的平面凸n边形,即是(表述形式略有改动): 上述推广命题本身是正确的,但文献[1]对它们的“证明”却是错误的. 为了看清文献[1]中的错误,下面我们摘录文献[1]对命题1的“证明”中的部分过程: 先证5顶点中必存在4个顶点共圆.假设每个顶点所在的“等圆三角形”至少有5个,每个“等圆三角形”至多被计算3次,那么“等圆三角形”至少有5×5÷3>8个.这与已知7个“等圆三角形”矛盾.故必存在一个顶点,含此顶点的“等圆三角形”不超过4个,那么剩下4个顶点至少有3个“等圆三角形”.由引理2(注:文献[1]中引理2即是本文中的定理1)知此4顶点共圆…… 上述“证明”中认为“等圆三角形至少有5×5÷3>8个”与“有7个等圆三角形”矛盾.由此反证假设不成立.显然,文献[1]是将命题1中“有7个是等圆”中的“有”理解成了“有且仅有”(或“至多有”).然而这种理解并不正确! 事实上,命题1的结论“5顶点共圆”显然蕴含了“10个圆都是等圆”的结论.若按上述“证明”中的理解,那就意味着由“有且仅有7个是等圆”(或“至多有7个是等圆”)的题设却推出了“10个圆都是等圆”的结论.但这两者明显相互矛盾,前者不可能蕴含后者. 我们认为:命题1中的“有7个是等圆”中的“有”的含义应当是“至少有”.这样,题设与结论间才不矛盾.但如果是“至少有”的意思,那么上述“证明”中推出的“等圆三角形至少有5×5÷3>8个”与题设“至少有7个是等圆”是可能同时发生的.也就是说,文献[1]的“证明”中由假设并未导出矛盾!这样的话,文献[1]使用的反证法就失效了. 综上所述,文献[1]对此命题的“证明”是不正确的. 而文献[1]对上面的命题2和定理3的证明中存在同样的推理步骤,所以犯有同样的逻辑错误,从而其“证明”也同样是不正确的. 由于对某些量词错误的理解导致在解答问题时不知不觉地犯下逻辑错误,这并不鲜见.但值得肯定的是:文献[1]给出的推广命题本身是正确的.当然,这需要重新证明. 我们先证明命题1.通过对此种具体情形的证明来介绍我们的思路. 命题1的证明先证5顶点A1,A2,A3,A4,A5中必存在4顶点共圆. 假设从5顶点中任取的4顶点都不共圆.结合定理1知:其中任4顶点构成的凸四边形中能产生的等圆不超过2个.而从5顶点中任取4顶点有5种取法,因此等圆不超过2×5个. 不过上面的计数方法会使得等圆被重复计数.我们需要知道每个等圆被计算了几次. 因此实际等圆个数不会超过5×2÷2=5个.这与题设“至少有7个是等圆”矛盾. 矛盾表明:5顶点A1,A2,A3,A4,A5中必存在4顶点共圆. 不妨设这两个有从A5出发的公共边的等圆三角形是△A1A2A5和△A1A3A5.注意到A1,A2,A3,A4共圆,因此△A1A2A3也是等圆三角形.这样,在凸四边形A1A2A3A5中就产生了3个等圆三角形.由定理1可知:A1,A2,A3,A5四点共圆.由此即得:A1,A2,A3,A4,A5这5点共圆.证毕. 下面我们用数学归纳法对一般情形进行证明. 定理3的证明当n=4时,由定理1知结论成立. 假设当n=k(k≥4)时结论成立,即: 当n=k+1时,我们需要去证明下面的结论成立: 先证k+1个顶点A1,A2,A3,…,Ak+1中必存在k个顶点共圆. 下面我们看看其中的每一个等圆被计算了几次. 对照上面n=k+1时的命题的题设,只需证明如下不等式即可导致矛盾. <(k-1)(k-2). (i)当k为奇数时,上式 ⟺(k+1)(k-1)-(k-2)(k+1)<(k-1)(k-2) ⟺k2-4k+1>0; (ii)当k为偶数时,前式 ⟺(k+1)(k-2)-(k-2)(k+2)<(k-1)(k-2) ⟺k2-2k>0. 在k≥4的条件下上面(i)、(ii)中的不等式显然都是成立的. 综上可知,能导致矛盾的那个不等式确实成立. 矛盾表明:假设不成立.所以,在顶点A1,A2,A3,…,Ak+1中必存在k个顶点共圆. 不妨设这两个有一条从Ak+1出发的公共边的等圆三角形是△A1A2Ak+1和△A1A3Ak+1.注意到A1,A2,A3,…,Ak共圆,因此△A1A2A3也是等圆三角形.这样,在凸四边形A1A2A3Ak+1中就产生了3个等圆三角形.由定理1可知:A1,A2,A3,Ak+1四点共圆.即Ak+1也在A1,A2,A3所确定的圆上. 由此即知:A1,A2,A3,…,Ak+1这k+1个顶点共圆. 所以,当n=k+1时结论也成立. 综上,定理3在n∈N且n≥4时都成立.证毕. 这样,我们就完成了对一般情形的重新证明. 或者也可以换个提法: 另外,文献[1]还提到了能否将定理3推广到3维空间的问题.对这几个相关问题,有兴趣的读者可继续研究.2 文献[1]的推广与证明中的逻辑错误

3 定理3的重新证明
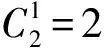


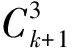
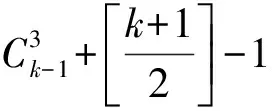
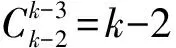

4 问题