高速铁路桥梁预制节段拼装桥墩抗震性能分析

梁岩，李庆贺，罗小勇，曹阳，张浩

(1.郑州大学 土木工程学院，河南 郑州 450000；2.中南大学 土木工程学院，湖南 长沙 410075)

桥梁传统现浇施工方式速度慢、污染严重且影响交通。节段预制具有生产标准化作业、现场安装快速便捷、施工节能环保等优势，较好地响应了新时代的桥梁建设理念，改善了现浇施工的不利影响，得到了愈加广泛的应用。预制节段拼装桥墩(Precast Segmental Bridge Column,PSBC)自1955年Pontchartrain桥采用以来，主要应用于低烈度区的公路桥梁工程中，中国近些年的桥梁也开始大量使用，港珠澳大桥的引桥非通航孔有62个桥墩采用节段预制拼装桥墩。关于PSBC抗震性能的研究，2000年后才逐步开展。HEWES等[1]研究了地震作用下PSBC的抗震性能，依靠预应力筋连接成整体的PSBC拥有比现浇墩(Monolithic Reference Column,MRC)更强的自复位能力；但由于节段间纵筋的不连续性和桥墩的摇摆性，其墩顶位移更大，且耗能能力更弱。为提高PSBC的耗能能力，使其能够适用于中高烈度区，OU等[2]改进了Hewes试验和分析方法，对2个钢管约束混凝土PSBC进行横向循环荷载试验。为进一步提高PSBC抗震性能，OU等[2−3]提出采用普通钢筋贯通PSBC的接缝，并将此贯通纵筋称为耗能钢筋。葛继平等[4]采用有限元方法分析Chou试验中的钢管约束混凝土PSBC的抗震性能。贾俊峰等[5]对在不同位置施加钢管约束的PSBC进行横向循环荷载试验，揭示了其在水平往复加载过程中的非线性力学行为。大尺寸PSBC使用大直径高强钢筋可减少纵筋数量，提高施工效率，FAN等[6]对大直径钢筋波纹管连接PSBC进行拟静力试验。近年来，国内外一系列PSBC试验表明，采用形状记忆合金[7]、FRP筋[8−9]以及UHPC[10−11]等材料，均可不同程度提高PSBC抗震性能及自复位能力。ZHANG等[12]提出一种用灌浆波纹钢套管和现浇UHPC榫头连接PSBC的混合连接方式。梁岩等[13−14]基于非线性时程分析，通过截面弯矩−曲率曲线研究了普通桥墩及拼装桥墩的抗震性能。依据某高速铁路桥梁工程，采用OpenSees分别建立MRC和PSBC 2种形式桥墩的有限元分析模型，通过非线性增量动力分析，计算PSBC的最大位移角、残余位移角、接缝张开相对变形和弯矩-曲率滞回曲线等指标，研究主要设计参数对预制节段拼装桥墩的抗震性能的影响。

1 MRC和PSBC桥墩有限元模型

1.1 模型建立

以某8度地区高速铁路三跨连续−刚构桥支座墩为例，设计地震为0.3g。MRC与PSBC桥墩设计形式和有限元模型见图1。保护层厚度为45 mm，上部结构恒载轴压比为0.034，内架立筋采用D12。MRC与PSBC桥墩满足等效原则：截面尺寸(26.32 m2)，体积配箍率(0.56%)，纵筋配筋率(0.91%)和材料(C45混凝土、HPB300箍筋、HRB500纵筋和耗能钢筋)均相同。桥墩等分为3个节段，采用金属波纹管灌浆法将耗能钢筋和预制节段拼装成整体。

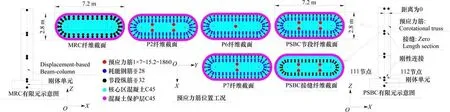
图1 桥墩设计形式和有限元模型Fig.1 Design form of bridge pier and finite element model

采用OpenSees建立MRC和PSBC有限元模型，PSBC模型约束条件和坐标轴方向与MRC模型一致。PSBC每个墩身节段均采用Displacement-Based Beam-Column单元模拟，沿长度方向设置5个积分点，底端节点固结，顶端节点释放约束。PSBC各节段接缝均采用ZeroLengthSection单元模拟，仅布置耗能钢筋纤维；在接缝截面边缘处设置4个节点，与墩身节点刚性连接，节点的竖向相对位移为接缝的位移；令接缝中部未设置连接材料的2个节点不能发生相对水平位移，但允许其发生相对转角位移，以实现其上下2节段间的张开闭合。无黏结预应力筋采用Corotational Truss单元模拟，Corotational Truss单元划分和墩身Displacement-Based Beam-Column单元对应。

1.2 模型验证

为研究PSBC与MRC抗震性能的差异，BU等[15]通过试验对4个不同配筋形式的缩尺PSBC试件和1个MRC试件对比分析，MRC除不存在节段连接外，其他参数均与PSBC相同，本文选择一个PSBC试件进行试验验证，试件见图2(a)。试件承台、墩身和盖梁采用C40混凝土；无黏接预应力筋配筋率为0.31%，初拉力为252 kN，轴压比为0.074 9，耗能钢筋配筋率为0.71%；S1节段箍筋间距为50 mm，体积配箍率为0.96%，其余节段箍筋间距为80 mm，体积配箍率为0.60%。依照文献[15]试件建立PSBC有限元模型见图2(b)，不考虑重力2阶效应。试验加载采用位移控制方式，按照0.1%，0.2%，0.3%，0.5%，0.75%，1%，1.5%，2.0%，2.5%，3.0%，3.5%，4.0%，4.5%，5.0%，6.0%和7.0%水平位移角，每级2次循环加载，水平位移角为墩顶水平位移与有效墩高的比值。

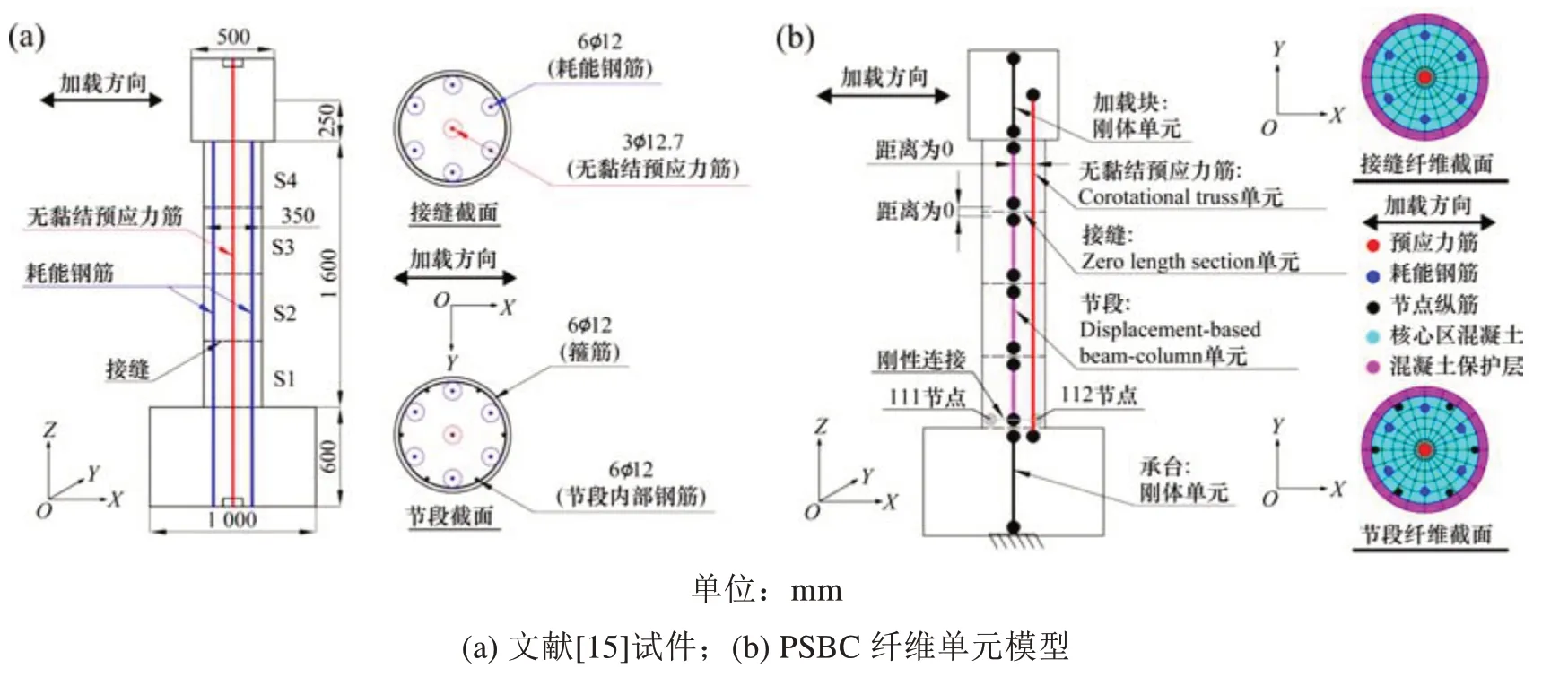
图2 PSBC模型Fig.2 PSBC model

有限元模型计算结果与试验对比见图3，试验过程中受加载方式、试验设备及荷载大小等诸多因素的影响，正反方向加载屈服后荷载位移曲线有所差别；有限元模型荷载-位移滞回曲线正反方向对称，有限元模型计算结果与试验反向加载吻合良好。图3(c)和3(d)为对比接缝和预应力筋结果，有限元模型和试验墩底接缝张开时最大位移约为15 mm和13 mm，闭合时最大位移均约为5 mm；有限元模型和试验模型正向水平位移角的预应力筋最大应力值分别为1 495 MPa和1 412 MPa，反向水平位移角的预应力筋最大应力值分别为1 484 MPa和1 550 MPa。有限元模型的结果与试验结果吻合较好，误差在合理范围内，建立的有限元分析模型可以用于MRC与PSBC的抗震性能分析工作。

图3 有限元与试验结果对比Fig.3 Comparison between finite element model and experiment result

2 动力时程分析

为研究MRC与PSBC在实际地震动激励下的地震响应，根据桥址场地条件：Ⅱ类场地，设计地震动分组为第2组，特征周期(Tg)取0.4 s，依据《公路桥梁抗震设计规范》(JTG/T 2231-01-2020)[17]本文算例阻尼比(ζ)取0.05。从美国太平洋地震工程研究中心的强震数据库中选取符合本地场地条件的3条地震动Imperial(震级6.9，PGA为0.28g)，Loma(震级6.9，PGA为0.17g)和Chuetsu-oki(震级6.9，PGA为0.11g)对PSBC和MRC进行动力时程分析，地震动加速度时程见图4。

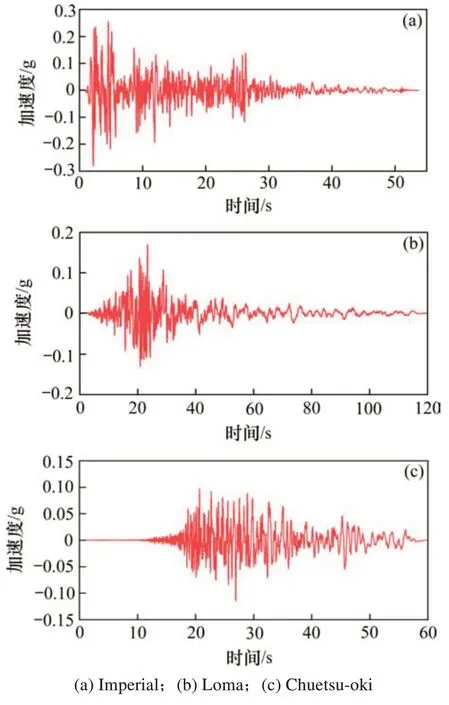
图4 地震动加速度时程Fig.4 Time-history of ground motion acceleration

本文采用增量动力分析(Incremental Dynamic Analysis,IDA)评价结构的抗震性能，通过绘制结构性能参数(Damage Measure,DM)与地震动强度参数(Ground Motion Intensity Measure,IM)曲线，研究结构在地震动激励下损伤破坏的全过程。DM选用墩顶最大位移角、残余位移角和墩底弯矩曲率等参数；IM选用地震动峰值加速度(Peak Ground Acceleration,PGA)。

采用OpenSees计算桥墩自振特性，MRC和PSBC的基本周期分别为0.84 s和1.24 s，本文实例桥墩周期小于2.0 s，选PGA作为地震动强度指标。基于IDA法将所选地震波在0.1g～1g范围内进行调幅，沿X轴方向(桥墩弱轴，纵桥向)输入，以研究不同PGA下最大位移角、残余位移角、接缝相对变形、最大预应力和弯矩−曲率变化的规律。地震动Imperia调幅至1.0g状态下的墩顶位移时程曲线见图5，定义最终位移削弱到不足最大位移0.5%时，结构不发生大幅度振动，则假定该位移为残余位移。为使MRC与PSBC模型具有充分的自由振动时间以得到更加准确的震后残余位移，毕仲君等[16]基于自由振动法取地震动零加速度段持时(自由振动时间)为结构基本周期的10倍左右。本文将地震动持时延长10 s以便准确获得结构震后残余位移。

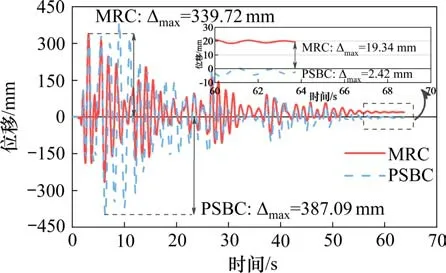
图5 Imperial-1.0g墩顶位移时程曲线Fig.5 Curve of Imperial-1.0 g top pier displacement time dependent

基于增量动力分析，计算在设计地震动0.3g，罕遇地震动0.57g和极大地震动1.0g[18]激励下，最大位移角和残余位移角随PGA变化情况，并对比分析MRC与PSBC地震响应。在设计地震动作用下，位移变化较小，以极大地震动1.0g为例，计算结果见图6(a)。PSBC墩顶位移角大于MRC，最大位移角增大约25%；PSBC残余位移角小于MRC，残余位移角减少约31%。以上现象的主要原因是接缝之间的张开闭合导致PSBC墩顶最大位移增大，预应力筋提供的自复位能力使PSBC残余位移比MRC小。

以地震动Chuetsu-oki为例，PSBC在不同地震动作用下墩底接缝相对变形随PGA变化的曲线见图6(b)。PSBC的墩底接缝相对变形均随PGA增加而增大，111节点最大墩底接缝相对变形约为83 mm，112节点最大墩底接缝相对变形约为30 mm。

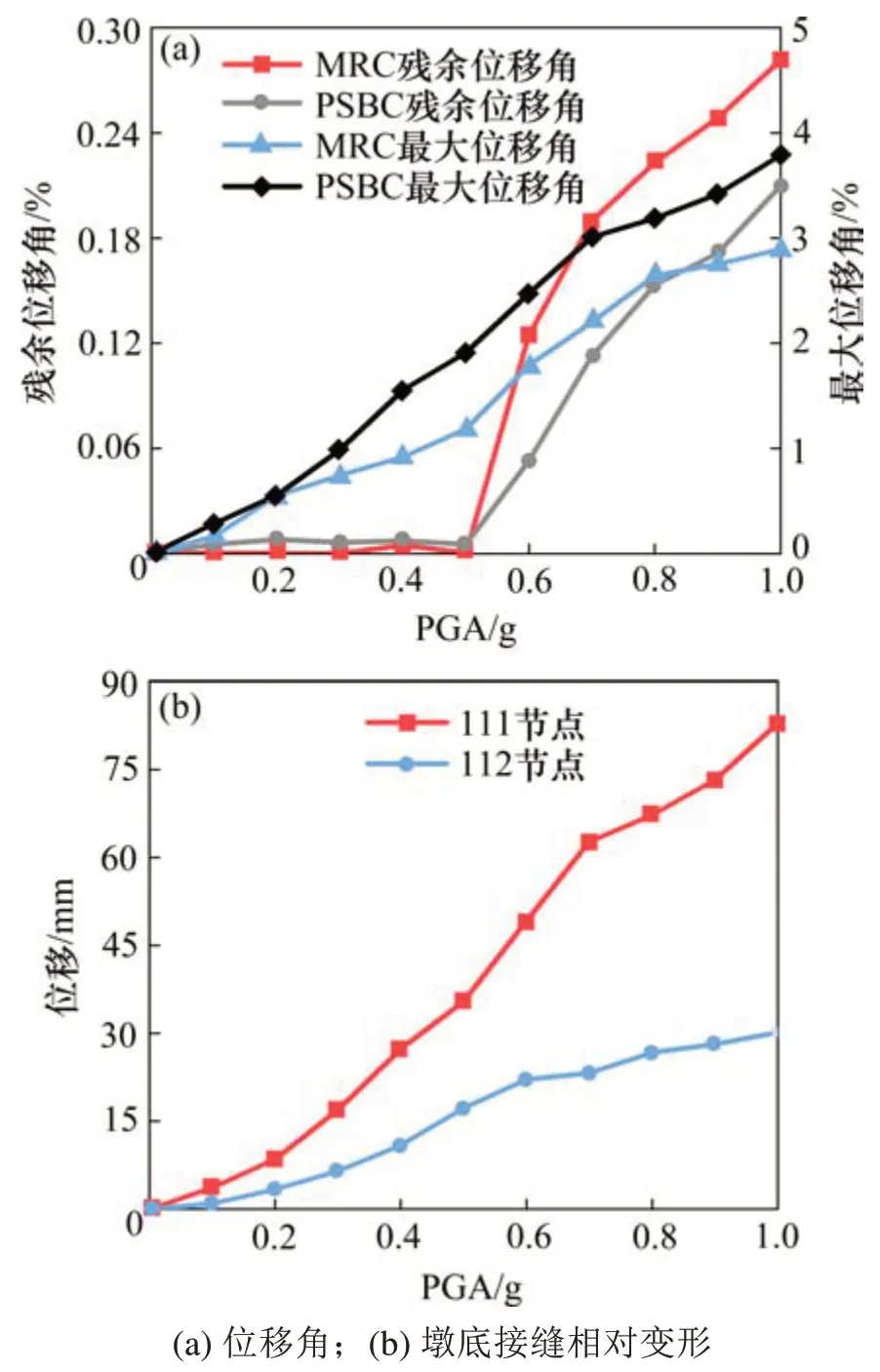
图6 位移变化曲线Fig.6 Displacement changing curves

根据动力时程分析结果，计算不同地震动激励下，PSBC和MRC的弯矩-曲率随PGA变化的滞回曲线见图7。MRC在各地震动下的弯矩-曲率滞回曲线更加饱满；在Imperial和Chuetsu-oki地震动下PSBC的弯矩-曲率滞回曲线与MRC相比，捏缩现象更明显；Loma波地震能量较小，MRC与PSBC在Loma地震动激励下的弯矩-曲率滞回曲线区别较小，地震动Imperial和Chuetsu-oki的能量较大，弯矩-曲率滞回曲线区别较大；以Chuetsu-oki-1.0g地震动为例，MRC墩底最大弯矩为20 682 kN·m，最大曲率为4.77×10−4m−1；PSBC墩底最大弯矩为17 834 kN·m，最大曲率为1.21×10−4m−1；MRC墩底最大弯矩约比PSBC大15%，最大曲率约为PSBC的3倍。

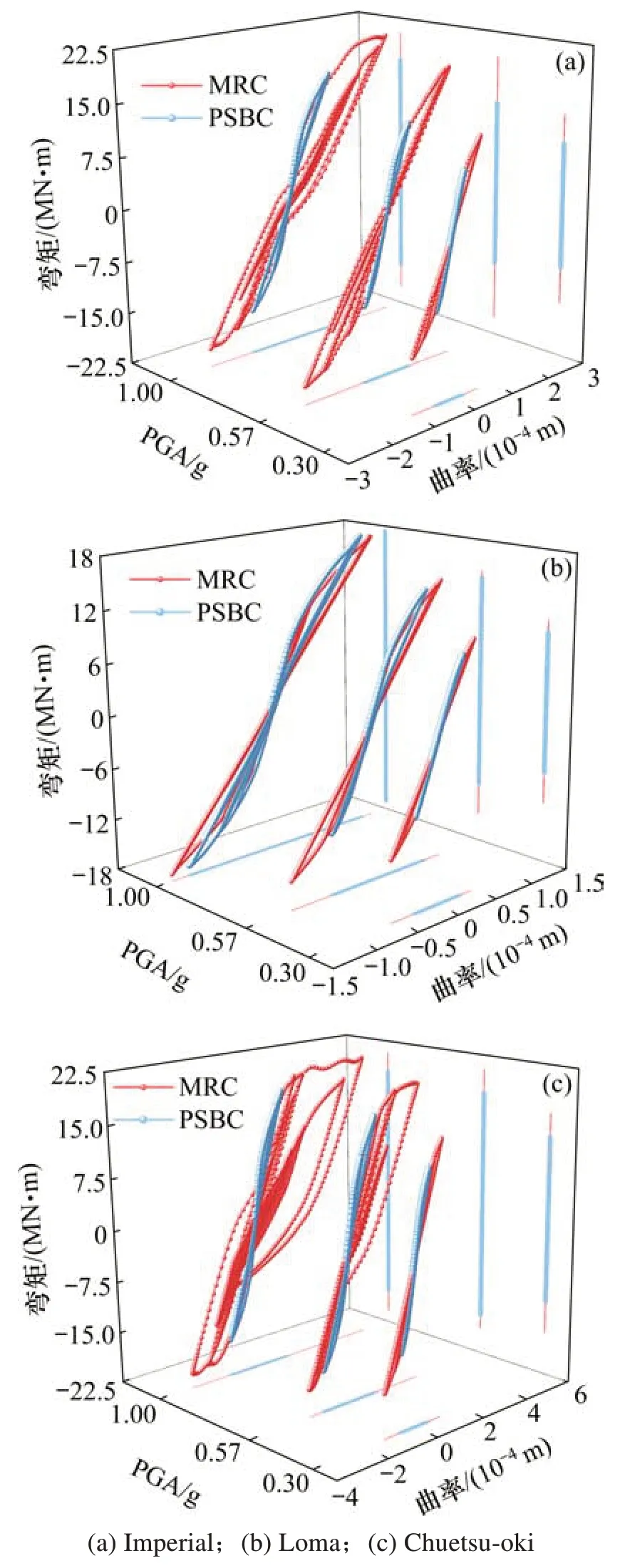
图7 弯矩-曲率滞回曲线Fig.7 Moment-curvature hysteresis curves

据夏修身等[19]的研究成果，循环荷载作用下预应力会发生变化，基于增量动力分析计算不同地震动激励下PSBC中的预应力值随PGA变化的趋势见图8。各地震动下的PSBC预应力筋最大应力均随PGA增加而增大，在能量较大的地震动Chuetsu-oki作用下，PGA从0.1g增至1.0g，预应力筋应力增长约30%。

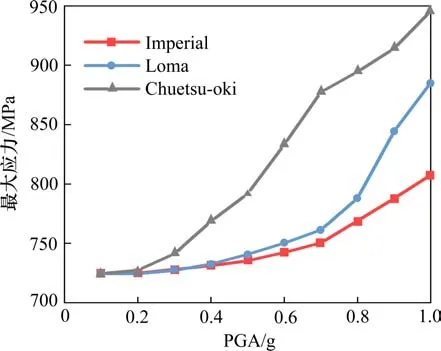
图8 预应力筋应力变化曲线Fig.8 Stress curves of prestressing-steel

3 PSBC设计参数分析

为研究PSBC在承载力、延性、耗能和自复位等方面的抗震特性，以最大位移角、残余位移角、预应力筋最大应力值和弯矩−曲率滞回曲线为量化指标，考虑耗能钢筋配筋率ρED，混凝土轴心抗压强度fc和预应力筋位置3个参数。在《铁路工程抗震设计规范》(GB50111—2006)中规定钢筋配筋率为0.5%～4%[16]，由BERRY等[20]的研究结果，桥墩纵筋配筋率一般不超过2.0%，耗能钢筋配筋率ρED取0.6%～2.0%。混凝土强度等级根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[21]以及经济实用性取C35～C50，设计7个PSBC模型见表1，预应力筋位置工况见图1，试件P1，P3，P4及P5的预应力筋位置与试件P2相同。

表1 动力时程参数分析工况Table 1 Dynamic time-history parameter analysis workingcondition

耗能钢筋配筋率、混凝土强度及预应力筋位置对PSBC的抗震性能影响见表2。墩顶最大位移、残余位移、墩底接缝张开相对位移和预应力筋最大应力均随PGA的增加而增大；耗能钢筋配筋率增加、混凝土强度提高、预应力筋分散布置，PSBC承载力提高，最大位移、残余位移角和墩底接缝张开相对位移均减小。地震动沿X轴方向(桥墩弱轴、顺桥向)输入，Y轴方向(桥墩强轴、横桥向)的预应力筋布置位置对X轴方向位移无影响，试件P7和P2的预应力筋均沿顺桥向布置，计算结果一致。分散布置预应力筋使其在地震作用下应力增大，充分发挥预应力作用，增强PSBC的抗震能力。

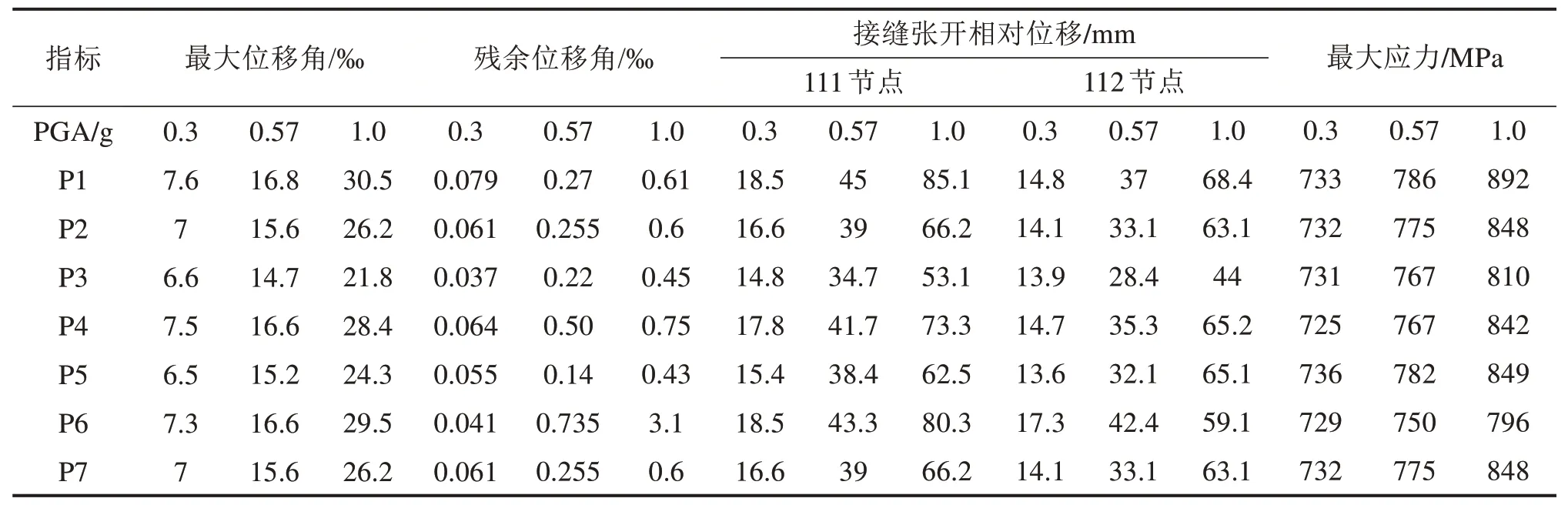
表2 动力时程计算结果Table 2 Dynamic time-history calculation results

设计地震作用下，不同耗能钢筋配筋率、混凝土强度、预应力筋位置下的墩顶位移、残余位移、接缝张开相对位移和预应力筋最大应力变化较小，对PSBC抗震性能的影响不明显。

在罕遇地震动0.57g作用下，耗能钢筋配筋率为0.6%～1.68%，墩顶位移、残余位移和接缝张开相对位移最大分别为1.68%，0.027%和45 mm，相对于耗能钢筋配筋率为0.6%和1%的试件P1和P2，耗能钢筋配筋率为1.68%的试件P3墩顶最大位移分别减少12%和6%，残余位移减少19%和13%，接缝张开最大相对位移减少23%和14%。耗能钢筋配筋率对PSBC桥墩抗震性能的影响随PGA增大而提高，当地震动从0.3g提升至1.0g，P3墩底接缝张开最大相对位移分别减少约11%和20%。与混凝土标号为C45和C35的试件P2和P4相比，混凝土标号为C55的试件P5最大位移分别减少约2%和%，残余位移分别减少约44%和71%，接缝张开最大相对位移分别减少3%和%。预应力筋沿桥墩四周布置的试件P2比在中间集中布置的试件P6的分别减少约6%墩顶最大位移、66%残余位移和22%接缝张开最大相对位移。

以极大地震动1.0g为例，耗能钢筋配筋率、混凝土强度和预应力筋位置对PSBC弯矩−曲率滞回曲线的影响见图9，地震动沿顺桥向输入，P7和P2的预应力筋沿X轴方向分散布置，弯矩−曲率曲线一致。PSBC耗能能力随耗能钢筋配筋率的增加而增大，耗能钢筋配筋率为0.6%～1.68%，最大分别为23 MN·m和1.3×10−4m−1。相对于P2，耗能钢筋配筋率最大的P3的弯矩、曲率分别增大28%和13%，预应力筋集中布置的P6的弯矩和曲率分别减少22%和37%，混凝土强度最高的P5的弯矩增大2%，曲率减少11%。预应力筋的分散布置可显著增大墩底弯矩；混凝土强度的提高，墩底弯矩增大，曲率减小。

图9 各参数下的弯矩-曲率曲线Fig.9 Moment-curvature curves on various parameters

4 结论

1)设计地震作用下，各设计参数对抗震性能的影响不明显。相对于MRC，PSBC有接缝，预应力筋等构造，PSBC的弯矩−曲率滞回曲线有较明显的捏缩现象，以极大地震动1.0g为例，PSBC的墩顶最大位移增大25%，残余位移减少31%，最大弯矩与最大曲率分别减少约13%和60%。

2)增大耗能钢筋配筋率、提高混凝土抗压强度和预应力筋分散布置均可有效减小地震作用下PSBC墩顶最大位移、残余位移和接缝张开相对位移。随着耗能钢筋配筋率的增大，每根钢筋承担的荷载逐渐减小，耗能钢筋应力减小，残余位移减小。在罕遇地震作用下，相对于耗能钢筋配筋率为1%，耗能钢筋配筋率为1.68%的墩顶最大位移减少6%，残余位移减少13%，接缝张开最大相对位移减少14%。混凝土强度提高20%，残余位移减少约44%；相对于预应力筋集中布置，分散布置后，墩顶位移、残余位移和接缝张开相对位移分别降低约6%，66%和22%。

3)增大耗能钢筋配筋率、预应力筋分散布置均会增大PSBC墩底弯矩和曲率，提高混凝土强度对其影响相对较小。极大地震作用下，耗能钢筋配筋率由1%提高到1.68%，弯矩和曲率分别增大28%和13%；相比于集中布置，分散布置预应力筋使得弯矩和曲率分别增大约28%和59%。