不同失稳形态黄土边坡的动力响应研究

2022-07-12梁庆国乔向进曹小平王丽丽

铁道学报 2022年6期

孙文，梁庆国,，乔向进，曹小平，王丽丽

(1.兰州交通大学土木工程学院，甘肃兰州 730070；2.兰州交通大学土木工程国家级实验教学示范中心，甘肃兰州 730070；3.甘肃省道路桥梁与地下工程重点实验室，甘肃兰州 730070；4.中国地震局兰州地震研究所黄土地震工程重点实验室，甘肃兰州 730000)

我国黄土地区分布广泛，随着国家西部政策的推进，黄土地区工程数量不断增多，结合西部地区抗震设防烈度普遍较高的特点，亟需针对黄土边坡地震失稳过程和机制开展进一步研究，完善相应的抗震设计依据[1-4]。一般来说，在地震过程中陡坡和缓坡的破坏过程差异明显，二者的地震动力响应和失稳机制也不尽相同[5-6]。以言志信等[7]、叶海林等[8]为代表，在边坡动力响应研究方面取得了丰硕的研究成果。在前人的基础上，近年来边坡动力稳定性的研究更加系统[9-10]。刘新荣等[11]针对三峡水库蓄水后微小地震频发的现象，通过振动台试验和离散元的结合，研究了频发微震作用下岩质边坡的损伤演化机理。夏坤等[12]通过数值模拟及大型振动台试验的方法，研究了地震作用下，西北地区黄土塬边坡加速度响应与坡高的关系。王兰民等[13]研究了黄土边坡在降雨和地震耦合作用下的动力响应，对该工况黄土边坡的失稳过程进行了分类。

目前，关于边坡地震动力响应研究，多集中在对PGA和Fourier变换的结果进行时域和频域分析上。相关的研究成果已非常丰富，研究方法也较为成熟。但是，Fourier变换这种频域分析方法较为单一、定性，无法反映信号的非平稳、持时短、时域和频域局部化等特性，需要一种更加精细的分析方法。小波包变换具有同时反映信号时域和频域特征的优点，因此本文引入小波包变换的分析方法[14]，分解加速度响应信号，得到不同频段的能量占比，以不同频段的能量占比变化为切入点，结合边坡的失稳破坏过程进行分析，以期为相关研究和工程提供借鉴。

1 模型试验设计

1.1 地震波加载方案

为排除在某单一地震波振动下，模型的失稳和动力响应为偶然特征现象，不能代表普遍规律的可能性，同时最大限度地利用模型，试验采用汶川汤峪波和El-Centro波两种波形，由弱到强交替加载的方式，加载工况共设计18个。第一台边坡模型坡度较陡，预计失稳所需振幅较小，设计加载前12个工况；第二台边坡模型坡度相对较缓，设计加载全部18个工况。加载工况见表1。

表1 地震波加载工况

1.2 模型设计

模型试验原型为天然黄土边坡，几何相似比为1∶20。通过正交设计，进行模型土的配比试验，最终确定以原状黄土∶重晶石粉∶锯末∶水=0.835∶0.04∶0.015∶0.11的配比进行模型重塑黄土的配制[15]。相似参数见表2。

表2 相似参数

试验在大型电伺服式振动台上进行。该震动台有效加载频率为0.1～50.0 Hz。第一台边坡模型坡度60°，坡高48 cm，第二台边坡模型坡度45°，坡高110 cm，边坡模型均采用分层压实的填筑方法。在填筑的过程中，在沿边坡中轴线断面相应位置埋入加速度传感器，编号分别为A1～A15和A1～A25。为了减弱“模型箱效应”的边界影响，增加底部的摩阻力，在模型箱侧面和底部分别铺设了聚乙烯闭孔泡沫板和水泥砂浆黏结的鹅卵石。两台试验模型及加速度传感器埋设位置见图1。

图1 边坡模型试验设计简图(单位：mm)

2 加速度响应信号的小波包变换

2.1 小波包层数及频段划分

小波包对地震波的低频部分和高频部分均可进行分解，此外，小波包分析能根据分析要求和信号特性选择相应信号频谱与频带进行匹配，是一种能对信号进行时频精细化分析的方法[14]。虽然在理论上，小波包分解的层数是没有上限的，但是，分解层数过低或过高都不利于对地震波信号的分析。小波包分解层数为[16-17]

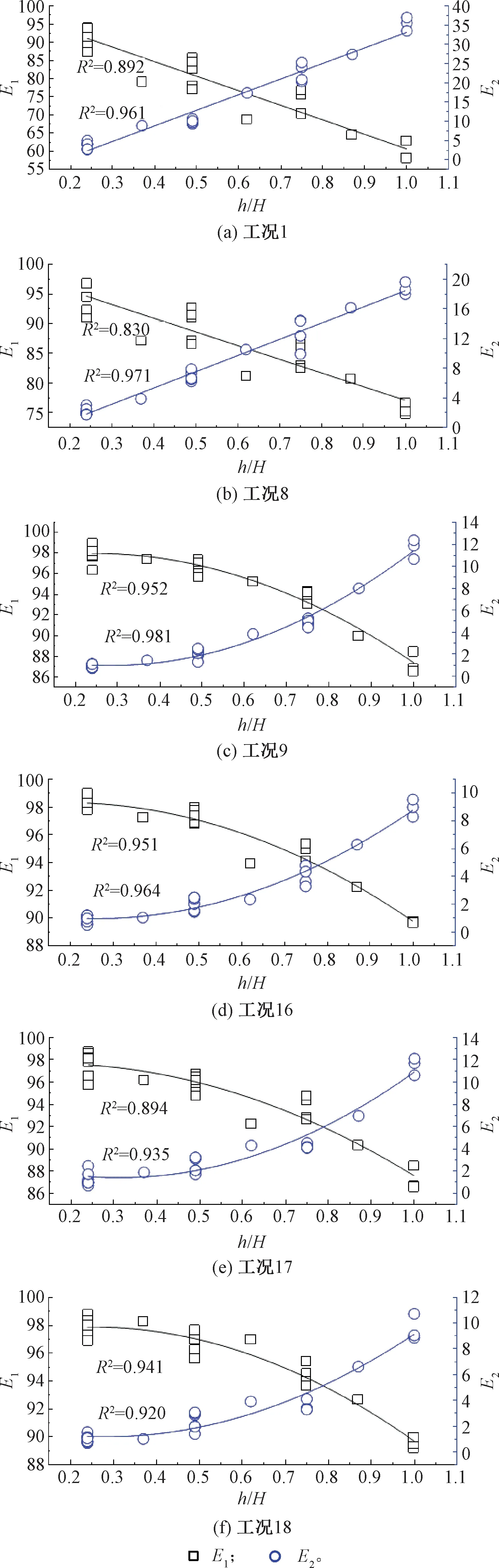
(1)

式中：k为分解层数；Ls为信号长度。

一般情况下地震波的持续时间为10～20 s，因此Ls取29～210，代入式(1)，得出k为0～9，综合考虑精细化和分辨率的要求后，本次试验的加速度响应信号k值取3层为宜。由于试验采用的地震波有效频率为0.1～50.0 Hz，三次分解后得出第三层小波包共有23=8个。参考Shannon采样定理[16]，设定采样频率为100 Hz。小波包分解后的8个频段范围见表3。

表3 频段序号及频段范围

2.2 小波包基函数选取

因为具有良好的紧支撑性、光滑性及近似对称性等优势，选用Daubechies(db小波)作为基函数进行信号的小波包分解。按照阶数，dbN小波基函数可分为db1～db10，试验选用db5小波基函数即可满足处理地震波信号的要求。利用Matlab，首先对加速度响应时程曲线进行Fourier变换，随后对Fourier变换得到的频谱信号进行小波包分解，然后对得到的各频段信号重构，最后对各频段进行能量占比的量化分析。

3 模型试验分析

3.1 边坡模型的失稳破坏过程分析

第一台边坡模型(模型一)试验的失稳破坏过程属于突发型，工况1～工况6(其中工况6X向输入加速度峰值XA=0.233g)期间，边坡上并未出现明显裂缝或其他破坏现象，工况7(XA=0.235g)加载时，边坡突然失稳破坏。在此后的加载工况中，坡脚、坡肩处进一步发生破坏，在工况10(XA=0.465g)的加载过程中，破坏更有加剧的趋势。工况7(破坏)之前、工况7(破坏)之后及结束加载后的模型见图2。

图2 模型一(突发型)

第二台模型(模型二)试验存在裂缝产生到发展再到大变形的过程，属于渐进型失稳边坡。工况1～工况8(其中工况8输入加速度峰值XA=0.235g)期间，边坡上未观察到明显裂缝或其他损伤；工况9(XA=0.465g)加载过程中，坡面两侧中部靠上位置出现裂缝；此后，坡面裂缝逐渐发育，在工况16(XA=0.705g)加载结束后，坡面裂缝贯通，其他部位无明显破坏；工况17(XA=0.935g)加载过程中，坡顶及其周边坡面局部出现了一定数量的裂缝；在工况18(XA=1.050g)的加载过程中，边坡失稳破坏，坡脚出现剪出面。边坡模型失稳破坏过程见图3。

图3 模型二(渐进型)

3.2 失稳过程中PGA的表现

排除采集有误的测点数据(模型一的测点A7、模型二的测点A4、A7)，绘制两台试验所有测点PGA随加载工况变化曲线，见图4。

图4 两台试验PGA随加载工况的变化趋势

由图4(a)可知，模型一(突发型)PGA随着加载的进行，有两次突变，分别出现在工况6(XA=0.233g)及工况10(XA=0.465g)的加载过程中。对边坡模型失稳过程的观察显示，在工况6加载结束后，边坡并未出现明显裂缝或其他损坏，边坡突然失稳是在工况7(XA=0.235g)的加载过程中发生的。在工况6加载时，虽然PGA值出现了突增现象，但是在边坡上并未观察到任何明显的裂缝或损伤，随后在工况7的加载中，边坡突然失稳破坏，可推断出在工况6加载结束后，边坡内部的损伤已经完成了量变到质变的积累，已处于极限状态。以极限状态为界，可以将突发型失稳边坡的失稳过程划分为破坏前(工况1～工况5)、极限状态(工况6)、破坏后(工况7～工况12)三个阶段。

由图4(b)可知，模型二(渐进型)随着加载的进行，PGA只有一次突变，出现在工况17，该工况加载时边坡裂缝恰好开始增多，变形明显加快。渐进型失稳边坡相较于突发型失稳边坡，其地震失稳破坏过程较为缓慢，边坡裂缝等损伤的发展易于观察。与突发型失稳边坡不同，渐进型失稳边坡的失稳破坏过程不存在明显的极限状态分界点，而是有一个裂缝从出现、发展直至贯通的过渡阶段。根据失稳破坏的特征，可将模型二(渐进型)的失稳过程暂时划分为弹性变形阶段(工况1～工况8)、塑性小变形阶段(工况9～工况16)、大变形失稳破坏阶段(工况17～工况18)三个阶段。因为工况1～工况8没有观察到裂缝，暂时认为属于弹性变形阶段，在下文小波包部分进行论证。

3.3 响应加速度的小波包分析

因篇幅有限，为了在避免繁冗同时，达到反映整个失稳过程中小波包分量变化情况的目的，仅选取具有代表性的特征工况进行分析。对于模型一(突发型失稳)，首先选取极限状态对应的工况6，其次选取破坏前阶段的工况1和工况5，以及破坏后阶段的工况7和工况10；对于模型二(渐进型失稳)，弹性变形阶段选取工况1和工况8，塑性小变形阶段选取两端的工况9和工况16，以及大变形失稳阶段仅有的工况17和工况18。

利用Matlab软件编制程序对加速度响应信号进行小波包变换，得到各频段的能量占比。第一频段(0.10～6.25 Hz)的能量占比用E1表示，第二频段(6.26～12.51 Hz)的能量占比用E2表示。经过分析发现，不管在哪个工况，各测点加速度响应信号的E1与E2之和均为90%左右，说明引起边坡动力失稳破坏的主要是振动波低频部分(0.10～12.51 Hz)。而且虽然各测点E1随高程增加而减小，E2随高程增加而增大，但E1始终大于50%，E2始终小于50%，说明主频始终是第一频段，次频始终是第二频段。绘制两台试验各自特征工况下所有测点E1、E2与高程的散点图，模型一、模型二分别见图5、图6(h为测点高程，H为坡高)。对应拟合曲线的结果见表4。

表4 E1和E2散点图拟合公式及相关系数

图5 模型一特征工况下E1和E2的高程规律

图6 模型二特征工况下E1和E2的高程规律

由图5可知，在破坏前(工况1～工况5)，突发型破坏边坡的E1和E2随着高程的增加分别显示出线性减小和线性增大的规律，随着加载的进行，从工况6加载开始直到工况7，E1和E2的高程规律转变为二次曲线型，说明在地震作用下，土体变形损伤不断累积到一定程度后，引起了边坡震动特性的改变，即3.2节提到的达到了极限状态，在后续加载过程中边坡突然失稳破坏。这验证了对突发型失稳边坡动力破坏过程的划分，以极限状态为界，可将突发型失稳边坡的失稳过程划分为破坏前、极限状态、破坏后三个阶段。

由图6可知：与模型一相同，模型二在工况1至工况8，E1和E2随高程的变化规律也分别表现出线性减小和线性增大的趋势，即弹性变形阶段；当加载至工况9时，E1和E2随高程的变化规律由线性转变为二次曲线，相应的，坡面开始出现裂缝，说明边坡地震变形损伤过程过渡到了下一个阶段，即塑性小变形阶段，验证了定义第一阶段为弹性变形的假定；在后续的加载中，边坡模型的损伤逐渐积累，但一直未发生整体失稳破坏，直到加载至工况17，开始发生大变形破坏。从工况9开始，E1和E2随高程的变化规律一直是二次曲线型。

通过对比两台模型试验的小波包分析结果可知，E1和E2随高程的变化规律由线性进入非线性时，边坡都出现了肉眼可见的破坏，从能量的变化规律，反映了在地震作用下边坡损伤逐渐积累，直到其动力特性产生改变的过程。可以此为依据，判断边坡是否即将发生破坏。

两台模型的主要区别在于：模型一的坡脚为60°，坡度较陡，抗倾覆及抗滑移能力差，对边坡损伤的允许值低，使得其地震失稳破坏是突然发生，且在大变形破坏前，基本无法通过肉眼观察到土体的损伤变形；模型二则不同，其坡脚为45°，坡度交缓，在地震作用时，下部土体对上部土体具有一定的抗滑作用，即使局部产生微小裂缝，也不至于很快造成滑动面的贯通，能够很好地“储存”或释放地震能量。坡度较缓的边坡在出现大变形破坏前可以承受更多的变形损伤。

3.4 反应谱分析

反应谱是指单自由度(单质点)体系在给定的地震作用下某个最大反应与体系自振周期的关系曲线，包括对加速度、速度和位移响应的反应谱分析。

在对加速度响应进行反应谱分析时，假设测点处土体是刚体单元，其加速度反应为

(2)

式中：ω为自振频率；h为临界阻尼；ωd为有阻尼的自振频率；ug(t)为激励加速度。

岩土体在地震作用下，土体内的损伤会不断积累，原有的微结构随之破坏，从而改变岩土体的固有频率或周期T，引起加速度响应的变化。因此，基于反应谱的岩土体地震研究需要注意特征周期T和反应谱幅值的变化。反应谱是基于弹性结构的地震动力反应绘制的，仍然把地震力作为静力对待，虽然引入了结构影响系数进行改进，但是只能得到土体结构进入弹塑性状态的整体反应，无法进行岩土体结构的精细化分析。因此，本文只对模型试验弹塑性小变形阶段进行分析。

为了便于分析，试验一对坡面测点A2、A3、A4、A5、A6随机选取极限状态前工况2、工况3、工况5、工况6进行分析，试验二对坡面的A10、A16、A17、A21、A22、A25测点取塑性小变形阶段的工况1、工况8、工况9、工况16进行分析。

出现最大值的反应谱曲线对应的周期即为特征周期，由图7可知，模型一(突发型失稳)，在加载至极限状态(工况6)之前，反应谱曲线显示其特征周期均为0.3 s，输入地震波强度的增加对反应谱幅值增益效果并不明显。加载至极限状态(工况6)时，边坡上部测点的特征周期变为0.2 s，边坡下部测点的特征周期变为0.35 s，反应谱幅值由3 m/s2剧增至9 m/s2。