受电弓弓头悬挂刚度的硬化及预测方法研究

刘久锐，周 宁，李 艳，刘 钊，张 欣，张卫华

(1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031；2.中铁二院工程集团有限公司，四川 成都 610031)

受电弓作为电气化铁路车辆系统受流装置的关键部件之一，在长期服役过程中其关键部件设计参数易于随时间发生变化，造成动力学性能退化，弓头悬挂系统亦是如此，其在服役期间性能的变化将直接影响弓网耦合质量。

并不局限于弓头悬挂系统，国内外的研究人员对于弓网系统中部分零部件性能、尺寸参数等发生改变对整个弓网系统的耦合所带来的影响已经通过建模仿真[1-5]进行了大量的研究。而对于受电弓的等效参数识别[6-7]和弓网接触时的接触力等数据的测量[8-9]也已经有了较大的进展。

值得注意的是，先前的大部分研究均是假定零部件性能参数已经发生了明确的变化，即人为在试验或者是仿真中设定其性能参数。而针对于其在服役过程中性能参数变化过程的研究仍然相对较少。为此，本文针对受电弓弓头悬挂系统，设计并开展其关键部件扭簧盒的硬化试验，以得到不同正弦波形加载幅值条件下扭簧盒的硬化曲线簇，并建立其硬化模型。在此基础上，对扭簧盒的刚度硬化值和模型的应用开展研究，以给出服役过程中受电弓弓头悬挂刚度的演变规律和预测方法。

1 弓头扭簧盒硬化试验

1.1 试验对象及装置

图1(a)所示为我国某型高速列车受电弓的三维模型，主要包括弓头、上框架、下框架、底座和绝缘子等几个主要部分，其中弓头部分的模型如图1(b)所示，弓头扭簧部件的局部模型如图1(c)所示。扭簧部件通过螺栓装配在受电弓套筒中，同时，在其辐板的端部通过直径φ6的通孔与弓头滑板部分相连。

试验时，液压作动器通过连接杆与扭簧盒辐板孔连接，设计合适的地面固定装置与扭簧盒连接并固定。通过作动器施加上下振动的位移波形，带动扭簧盒实现来回的转动。

1.2 试验载荷及工况

经试验及分析可知，扭簧盒在服役过程中发生的是类似于正弦波的上下振动，同时，考虑试验台的加载限制，将试验工况设定为加载曲线均为正弦波，对五组型号相同的扭簧盒分别进行不同次数及不同幅值组合下的硬化试验，以尽可能获取扭簧盒在不同工况下刚度的硬化规律，该试验分为两个大组，其加载数据见表1。

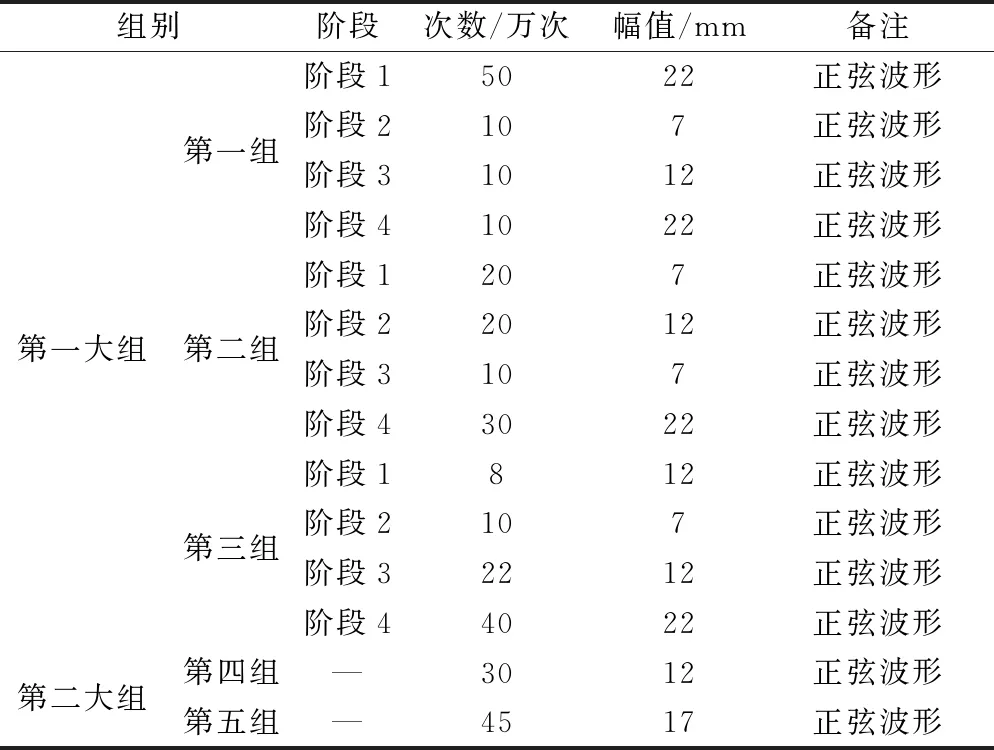
表1 试验加载数据

1.3 硬化试验结果

前三组的试验可得其散点数据，并用分段直线连接数据点以显示其变化趋势，如图2(a)所示。在此基础上，得到扭簧盒在不同幅值下的等幅循环硬化散点数据及其分段直线拟合曲线，如图2(b)所示。

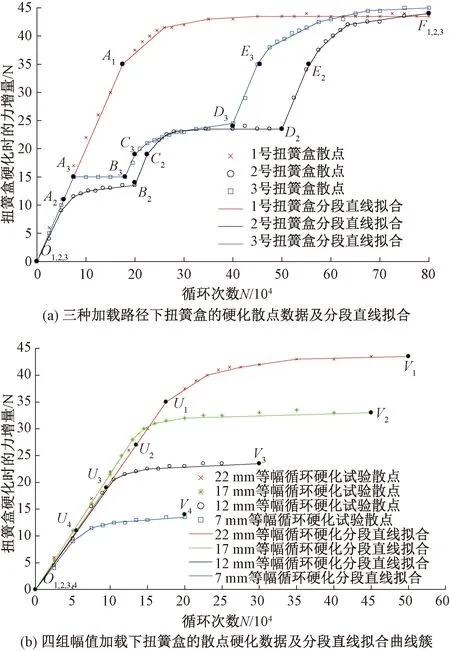
图2 扭簧盒硬化试验结果及其拟合数据

由图2可知，扭簧盒的硬化趋势可以分为两个阶段：早期的准线性硬化阶段(如：O1,2,3—A1，O1,2,3,4—U4段)和后期的准对数硬化阶段(如：A1—F1,2,3，U4—V4段)；当施加的应变幅值较小时，在一定的循环周次后循环硬化将会达到一个有限的饱和值，此时该幅值下的硬化试验将不再对扭簧盒产生硬化效果，即硬化饱和[10-11](如：O1,2,3—D3段 )；对于不同幅值下的硬化情况，遵循幅值越大硬化饱和值越大的规律，其中，循环硬化行为不仅依赖于循环周次，而且还取决于应变幅值的大小；由A3—D3，D2—F1,2,3…硬化情况可见，该扭簧盒的硬化过程未表现“记忆”效应[10-12]，也意味着无论之前加载到扭簧盒的位移曲线(如次数，幅值，频率，波形等)如何，该扭簧盒之后的硬化方式与此前的加载历史无关，只跟后续的加载方式有关；经过大量的试验测试和观察，在排除扭簧盒上螺旋扭簧对扭簧盒硬化现象的影响后，发现扭簧盒的硬化主要来自于扭簧盒上的止挡杆部分。止挡杆在使用过程中的反复弯扭使其发生循环硬化，并导致扭簧盒的整体刚度变大。根据上述特点，建立对应的硬化模型。

2 建立硬化模型

2.1 准线性部分

对于线性部分而言，无论循环幅值的大小，这一部分的曲线变化情况类似，基本遵循每5 000次循环增长1 N的规律，因此这一部分硬化值Feq1的表达式为

( 1 )

式中：Feq1为硬化值；N为循环次数；Nt为线性部分定义域上界。

2.2 准对数部分

对于准线性增长部分的上限Nt，通过试验发现该值与等幅循环时的幅值A有关，通过图2拟合出的硬化曲线中的准线性增长部分，其表达式为

Nt=8 000A0≤A≤22 mm

( 2 )

式中：A为等幅循环的幅值，mm，在本次试验中，其变化范围为0≤A≤22 mm。

还需给出一个准对数增长部分的增长上限，即饱和硬化的饱和值Feqmax，经过试验发现该值同样与A有关，其拟合表达式为

( 3 )

根据文献[10]，背应力X的表达式为

项目化管理是企业在面对复杂多变的市场环境下进行市场营销的一项重要管理策略。企业在日常的营销过程中，应该把项目化管理理念和营销技术有机结合运用，并不断增强企业营销管理过程的系统性与科学性，这样，企业的市场营销才会更加具有竞争力，从而有利于企业的不断发展壮大。

( 4 )

式中：ν′=±1，描述了流动的方向；X0、εp0、C/γ分别表示背应力与塑性应变εp的初始值以及材料硬化达到饱和时的饱和值。根据实际情况，这里选ν′=1，C/γ=2A，X0=0，εp0=0，可以得到

( 5 )

式中：Feq2表示的是准对数部分硬化增长值。为更方便的应用该模型，针对式( 5 )可作进一步的推导和简化。已知式( 5 )定义的硬化曲线必过(0,0)与(Nt,Nt/5 000)两个点，同时定义γεp为一个与N和A相关的函数，即γεp(N,A)，则有：当N=0时，无论A的大小，Feq2均为0，即γεp(0,A)=0；当N=Nt时，无论A的大小，Feq2=Nt/5 000=1.6A，即γεp(Nt,A)=1.6A。

根据以上两点，可以拟合出比较简单的γεp表达式为

γεp=ln5(N/Nt)

( 6 )

将式( 6 )代入式( 5 )，可以得到关于Feq2的简化表达式为

( 7 )

根据上述推导，综合准线性部分和准对数部分的硬化表达式，最终可得到该扭簧盒硬化模型的简化方程为

( 8 )

由式( 8 )得到的仿真曲线与硬化试验散点数据的对比,如图3所示。

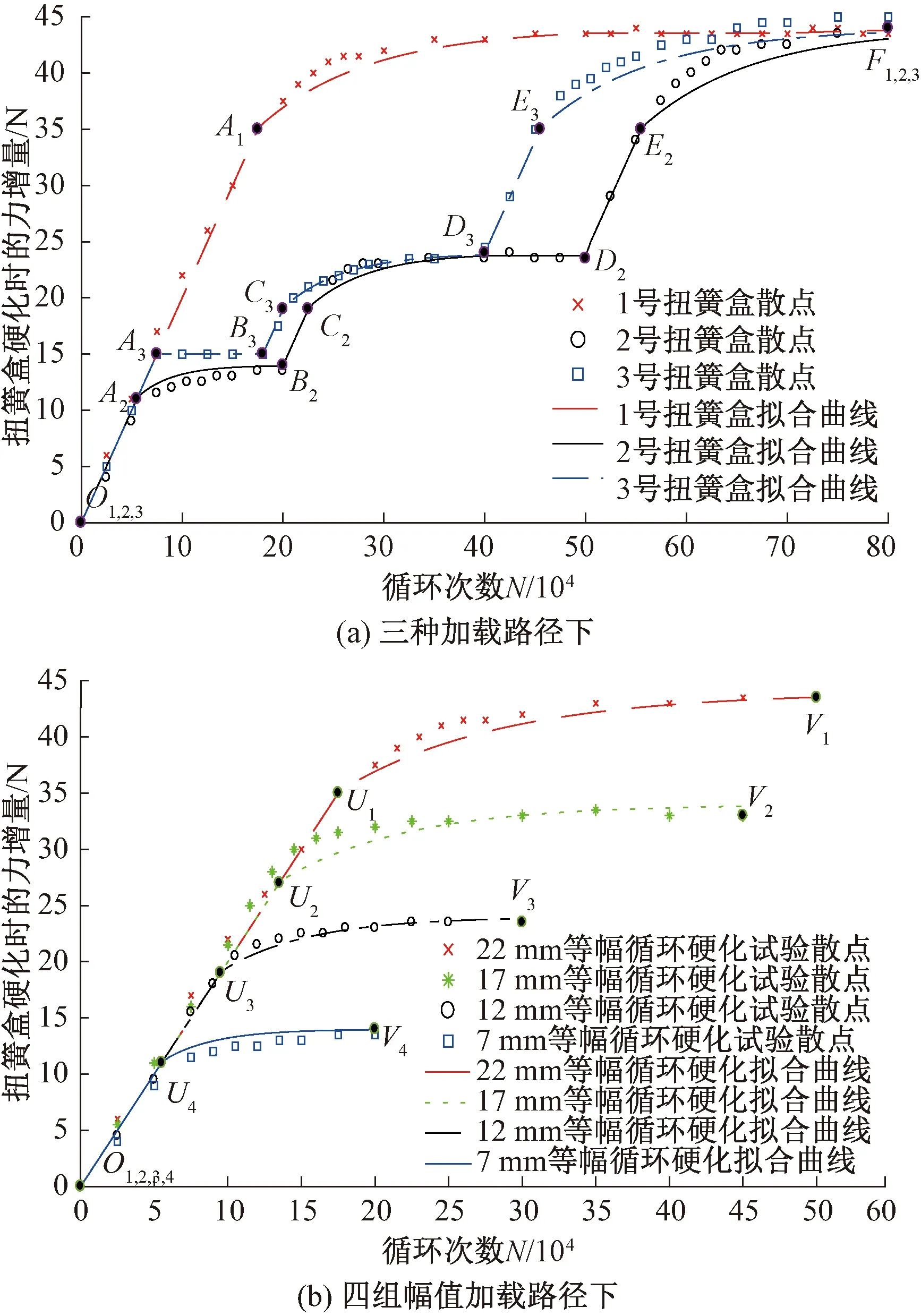
图3 扭簧盒硬化散点试验结果与模型仿真对比

图3表明，硬化模型可以较好地对扭簧盒在正弦波形不同幅值及不同次数加载条件下得到的硬化结果进行描述。但实际使用时扭簧盒的运动方式更加复杂，因此，该模型不能直接应用于工程中。

3 硬化模型应用

在实际工程应用中，直接获取悬挂系统的振动位移是比较困难的。为此，介绍一种通过获取外载荷来确定悬挂系统振动位移的方法。通过应变片测得辐板的应变，依据转换关系确定作用在弹簧盒的外载荷，基于动力学方程，确定扭簧盒的振动位移并确定扭簧盒的应变。最后，得到相应的硬化值。

3.1 扭簧盒辐板处应变与外载荷关系

图4 辐板上几何和应变关系

( 9 )

(l′+l′ε′)2=(lx+lxε)2+(lz+νlzεz)2

(10)

式中：My为应变片位置辐板承受的弯矩；Fy为辐板承受的垂向力；l为辐板方向的等效长度；ε为辐板方向的应变；y为应变片表面到中性面的距离；ρ为中性轴的圆弧半径；E为杨氏弹性模量；ν为泊松比；Iz为转动惯量；ε′为实际测得的应变；εz为z轴方向的应变；l′为应变片总长；lx为x轴方向长度；lz为z轴方向长度。

将测得应变ε′代入式(10)可得z轴方向的应变εz，代入式( 9 )可以得到垂向力Fy。将该扭簧盒的运动方式考虑为单自由度下的受迫运动来求解位移[13]。

3.2 振动位移波形预处理

弓网滑动接触过程中，作用在受电弓弓头的载荷较为复杂，导致弓头扭簧盒呈现准正弦波形的振动形式。图5给出了某一高速受电弓以300 km/h的速度运行时，弓头和上框架间的振动位移曲线，即弓头悬挂中扭簧盒的振动曲线。

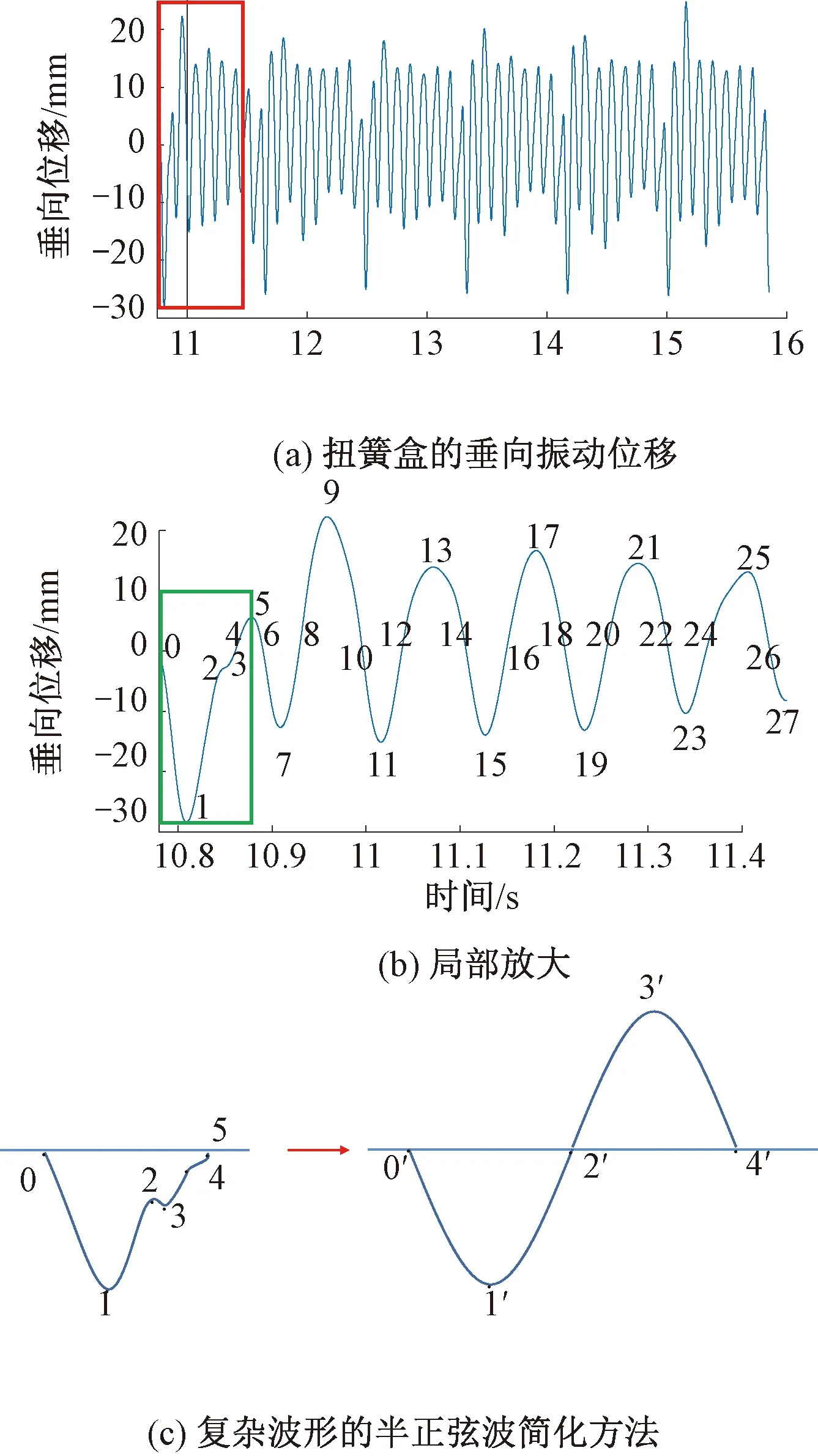
图5 弓头悬挂局部垂向位移及其简化

如图5所示，扭簧盒的实际位移曲线比较复杂，为此需要将复杂波形简化成可以代入到硬化模型中的正弦波形。借助雨流计数法的思路[14]，提出一种“分段-半周期统计”的处理方法。

Step1首先对图5(b)中曲线进行标注编号，总计28个点。

Step2对该组波形进行分段，分段的基本原则是：从上一个零位移处到下一个零位移处之间的这段波形作为一段，如：“8—10”段为一段，“10—12”为一段，“12—14”为一段等。

Step3需要注意的是只统计幅值为负的波形，如：“0—4”段，“6—8”段，“10—12”段等，原因在于扭簧盒在实际使用中只有幅值为负的扭簧位移发生时挡块才能带动止挡杆发生形变。

Step4逐个对分号段后的幅值为负的每段波形进行平滑处理，如：在“0—4”段中有一段“2—3”明显存在异常。对此，忽略“2—3”段的影响并直接将“0—4”段转换为正弦波形式，即以“0”和“4”之间的时间间隔Δt作为正弦波半周期的长度T/2，并以该段中的峰值点“1”到虚线y=0处的垂直距离为幅值A，作出修正后的图形，如图5(c)所示。用半个正弦波代替原有的波形，并且在后面的“4—6”段补上余下的半个正弦波，这样就得到了一组完整的上下幅值相同的正弦波形，从而完成复杂波形的简化。

Step5重复Step4，直到整组波形处理完毕，如图6所示。

如图6(a)所示，在使用“分段-半周期统计”方法处理位移波形图时，首先应该对其进行前处理，使用绿圈和粉色星号标出该位移曲线的所有零点和波谷的位置，即找到每段正弦波形的波长和幅值，再依据图5(c)给出的复杂波形的正弦波半周期简化方法，得到后处理图，如图6(b)所示。最后，统计得到的后处理图中负位移半正弦波的幅值及其次数，即是硬化模型的输入量。

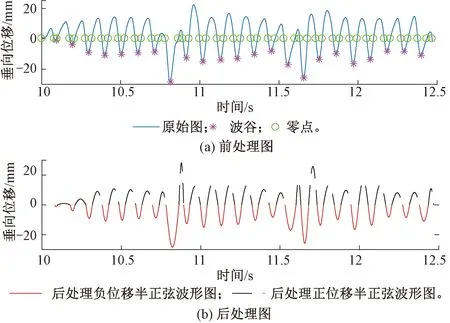
图6 分段-半周期统计处理示例

3.3 扭簧盒刚度硬化值

通过对扭簧盒振动位移的处理，可以得到正弦波相应的振动幅值和频次，代入硬化模型的简化公式式( 8 )中，可以得到该型扭簧盒的刚度硬化值。

在实际应用过程中，由于止挡杆刚度K杆(N,A)是与振动幅值A和频次N相关并动态变化的，同时处在不同的硬化阶段其硬化的快慢也不同，由此在确定振动位移以及相应的硬化值时，需要采用一种“分段循环”的计算方法，其基本流程如图7所示。

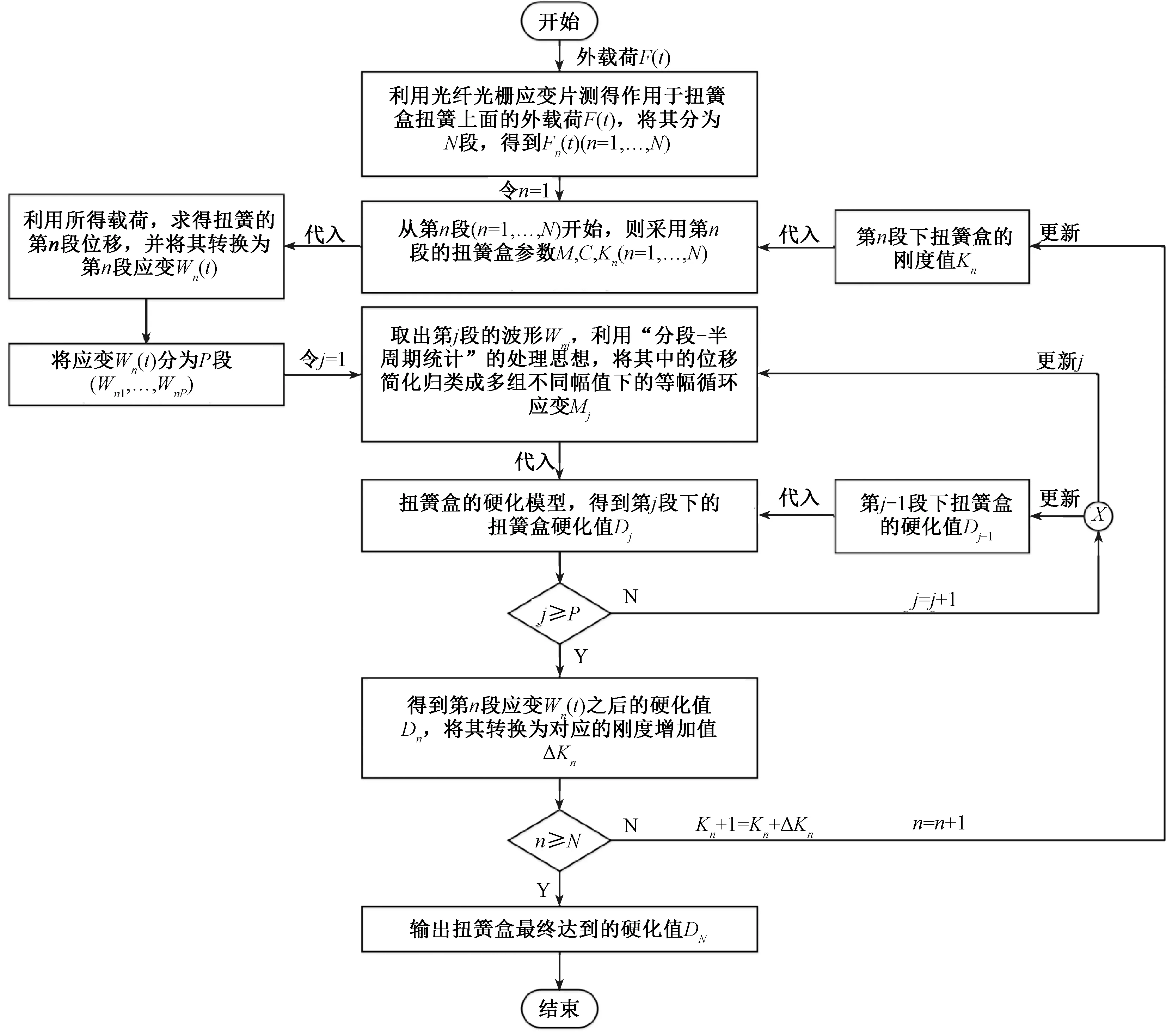
图7 输入载荷转换成扭簧盒最终硬化值流程

Step1利用光纤光栅应变片测得作用于扭簧盒扭簧上面的载荷F(t)，对其分为N段(如：每105个数据点分为一段)，得到Fn(t)(n=1,…,N)。

Step2假定从第n段(n=1,…,N)开始，采用第n段的扭簧盒参数M，C，Kn(n=1,…,N)，其中，归算质量M和阻尼C不变，并且利用所得载荷，确定扭簧盒的第n段应变Wn(t) 。

Step3引入在该扭簧盒上的应变波形Wn(t)，并将其按照固定长度分为P段。依次取出其中的各段波形Wnj(j=1,…,P)，并按照3.2节提到的“分段-半周期统计”的处理思想，将其中的位移波形转换成为相应幅值下等幅正弦应变波形，并统计不同幅值下各个波形的循环次数，将其简化归类成多组不同幅值下的等幅循环应变Mj。

Step4将Mj和此时扭簧盒的硬化值Dj-1代入到硬化模型中，并判断j是否大于等于P，若是，则说明整个波形Wn(t)处理完毕，则输出第n段应变Wn(t)之后扭簧盒达到的硬化值Dn；若j小于P，说明还有剩余的波形尚未处理，令j=j+1，并将新得到的扭簧盒的硬化值Dj作为新的扭簧盒硬化值保存并代入到下一轮的计算中，如此反复计算直至j≥P为止。

Step5得到Dn后，将其转换为第n段应变Wn(t)后扭簧盒对应的刚度值增量ΔKn，判断n是否大于等于N，若是，则说明整个外载荷F(t)处理完毕，输出扭簧盒最终达到的硬化值；若n小于N，说明还有剩余的载荷尚未处理，令Kn+1=Kn+ΔKn，更新下一个循环中扭簧盒的参数值Kn，并且令n=n+1，如此反复计算直至n≥N为止，得到扭簧盒最终达到的硬化值DN。

Step6重复Step2～Step5，直到整个载荷处理完毕，得到扭簧盒最终的刚度值。

4 结束语

弓头悬挂对于受电弓的安全运行有重大意义。为了研究弓头扭簧盒在服役过程中出现的刚度变化现象，本文提出一种扭簧盒刚度硬化模型，该模型是在对扭簧盒展开硬化试验的基础上，结合金属材料硬化的相关理论得到的。在此基础上给出一种利用光纤应变片确定扭簧盒振动位移进而确定扭簧盒硬化值的方法，该方法通过应变片测量扭簧盒所受外载荷，计算得到扭簧盒的振动位移，最后利用“分段-半周期统计”方法将复杂波形简化为可以代入到硬化模型中的正弦波形。结果表明硬化模型能够较好地描述扭簧盒的刚度动态变化曲线，为预测弓头悬挂系统刚度变化提供了一种行之有效的方法。