最优聚类的k-匿名数据隐私保护机制
2022-07-12叶阿勇叶帼华邓慧娜陈爱民
张 强 叶阿勇 叶帼华 邓慧娜 陈爱民
(福建师范大学计算机与网络空间安全学院 福州 350117) (福建省网络安全与密码技术重点实验室(福建师范大学) 福州 350117)
大数据时代中,数据资源具有可复制、可共享、无限增长和供给的属性,能够打破传统要素有限供给对增长的制约.数据也因为互联网及人工智能技术的赋能,成为推动社会经济发展变革的新“石油”[1-2].如今,数据已和其他要素一起融入经济价值创造过程之中,对生产力发展具有广泛影响.在该过程中,越来越多的用户数据被政府部门和服务提供商进行流通共享,主要用于数据挖掘和数据发布.然而,数据发布共享在给人们带来便利的同时,也增加了相关个体或组织泄露隐私信息的风险[3-4].例如,疾控中心需要收集各医院的病例信息用于疾病预防与控制,而这些病例信息中往往就包含病人不希望被揭露的敏感数据(所患疾病).因此,必须对公开发布的数据采取一定的隐私保护方法,防止攻击者通过背景知识或链接攻击等手段获取到用户隐私信息[5].
k-匿名(k-anonymity)模型是一种重要的个体隐私保护模型,近年来备受关注[6-7].该方法要求共享数据中存在一定数量(≥k)在准标识符上不可区分的记录,使攻击者最多只能以1/k的概率通过准标识属性关联出标识属性,从而保护了个体的隐私.k-匿名能有效防范链接攻击,但面对复杂的背景知识攻击时,攻击者仍然有可能以较高概率推断出个体与敏感信息之间的关联关系.因此,研究者在k-匿名的基础上又提出基于聚类的k-匿名技术.其基本思想是:先将待发布的数据集划分为若干簇,然后将每个簇内记录的准标识符泛化为相同的属性值,生成等价类,从而实现数据集的匿名化[8-9].然而,现有基于聚类的匿名方法大都是通过寻找最优k-等价集来平衡隐私性与可用性.从全局看,k-等价集并不一定是满足k-匿名的最优等价集,因此,隐私机制的可用性仍然不是最优.如图1所示,待匿名的准标识属性包含6个数据,如果采用经典k-匿名的聚类方法,如KACA聚类匿名方法(k-anonymisation by clustering in attribute hierarchies)[10]和GAA-CP聚类匿名方法(greedyk-anonymity algorithm based on clustering partition)[11]等,它们的基本思想是把6个数据进行均匀2-匿名聚类,那么数据集将被划分成3个等价集,如图1(a)所示,通过计算可得匿名数据集的总方差为131.但图1(b)的聚类结果也满足2-匿名要求,其方差为27.64.很明显,现有的聚类匿名方案无法实现最优的数据聚类结果.
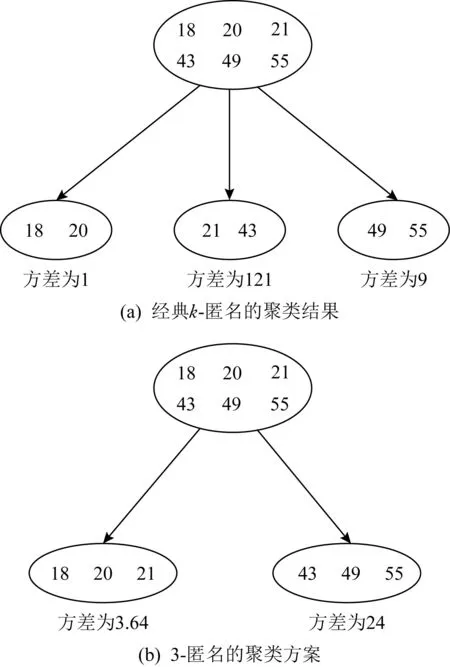
Fig. 1 k-anonymous clustering methods图1 k-匿名聚类方法
为了解决以上问题,本文提出一种基于聚类的最优k-匿名数据隐私保护机制.通过建立数据距离与信息损失之间的线性关系,将k-匿名模型中的可用性最优化问题转化为数据集的最优聚类问题,并利用贪婪算法和二分机制寻找满足k-匿名约束条件的最优等价集,从而实现满足隐私性下的数据可用性最优化.我们采用真实数据集进行实验分析,结果表明,在相同隐私约束的条件下本文方案展示了最小的信息损失.此外,当数据之间相似性增大时,它在隐私和可用性权衡方面的优势将会变得更大.我们还展示了本文方案的效率,发现本文的数据匿名时间明显优于其他匿名方案.
1 相关工作
k-匿名作为一种有效的数据匿名手段,可以有效防止隐私泄露,自提出以来已经被广泛应用于多个领域.Sweeney[12]在2002年提出了k-匿名模型.该模型保证攻击者不能在准标识属性上区分2个记录,因为每个用户被攻击者正确识别的概率最多为1/k.k-匿名能有效防范链接攻击,但面对复杂的背景知识攻击时,攻击者仍然有可能以较高的概率推断出个体与敏感信息之间的关联关系.因此,研究者在k-匿名的基础上提出基于聚类的k-匿名技术.
2006年,Aggarwal等人[13]在k-匿名中引入了聚类方法.Li等人[10]应用聚类思想,提出了一种KACA匿名算法,它的主要思想是在匿名过程中循环合并等价类,直到所有等价类包含k个元组以上.该方法需要预定义所有的准标识属性,并且没有考虑敏感属性多样性特点,这样会固化泛化模式,造成过多的信息损失.因此,王智慧等人[14]在文献[10]基础上考虑了敏感属性多样性,提出了一种l-聚类方法,它能够满足数据共享中对敏感属性多样性匿名的要求,减少了因过度泛化导致的信息丢失,但是该方法优先考虑l-多样性,在具体实现中可能会出现无解的情况.Liu等人[15]提出一种个性化扩展(α,k)匿名模型来满足个性化的隐私保护需求,根据敏感属性的敏感程度将敏感属性值分成若干组,并为每组限定属性值的出现频率,但是其没有考虑敏感属性的多样性问题.刘晓迁等人[16]提出了一种基于匿名聚类化的差分隐私保护数据发布方法,对匿名划分的数据添加拉普拉斯噪声,扰动个体的真实数据,然而该方法只针对数值型数据,并没有研究分类型和混合型数据发布隐私保护方法.因此,姜火文等人[11]利用贪心法和聚类划分的思想,提出一种GAA-CP匿名算法是通过分类概化数值型和分类型准标识属性,并分别度量其信息损失,聚类过程始终选取具有最小距离值的元组添加,从而保证信息损失总量趋于最小,但是该方法不能保证最优的聚类结果.文献[17]提出一种实现k-匿名性的新方法,在计算数据记录之间的距离时考虑了准标识符属性和敏感属性之间的联系、它们对敏感隐私的影响以及匿名过程中的信息丢失.同样,差分隐私技术也可以引入聚类方法,Ni等人[18]提出了一种差分隐私保护的k-means聚类方法,通过添加自适应噪声和合并聚类,显著提高了聚类的效用.具体来说,为了获得差分隐私的k簇,算法首先生成k个初始质心,每次迭代添加自适应噪声得到k簇,最后将这些簇合并到k簇中.将聚类合并和自适应噪声结合使用可以进一步显著提高其效用,但是该算法因迭代过程复杂而影响实用性.Wang等人[19]提出差分隐私来释放异构数据进行聚类分析,通过将聚类问题转化为分类问题来解决这个问题.该方法对原始数据进行概率泛化,并在原始数据中加入噪声以满足差分隐私.但该方法不适用于分布式数据发布.为此,Wang等人[20]又提出一种任意分区数据的差分隐私数据发布机制,在半诚实模型中用任意划分的数据匿名化双方数据的差分隐私方案且提出了一种分布式差分隐私匿名算法,保证该算法的每一步都满足安全双方计算的定义.
综上所述,现有的数据隐私保护机制不能解决k-匿名模型中数据可用性的最优化问题,无法最小化信息损失.因此,本文提出一种基于最优聚类的k-匿名隐私保护机制,利用贪婪算法和二分机制寻找满足k-匿名约束条件的最优聚类,从而实现k-匿名模型的可用性最优化.
2 预备知识
在一般情况下,数据是以2维表数据形式进行共享.表数据中每一行记录对应一个个体,每一条记录又包含多个属性,这些属性大致可分为4类:标识属性(ID)、准标识属性(U)、敏感属性(V)和其他属性(N).标识属性是指可以直接区分个体的属性,例如姓名、身份证号码和电话号码;准标识符属性是指通过链接可以推断出个体身份的属性,如性别、年龄和家庭地址等;敏感属性是指包含隐私信息的属性,如疾病和年收入等.表1为待发布的原始数据集,其中“Name”为标识属性,“Gender”“Age”“Zip”为准标识属性,“Disease”为敏感属性.数据隐私保护的本质就是要切断敏感属性与标识属性的联系,防止攻击者在两者间建立一一对应关系.此外,链接攻击可以从准标识符属性推断出个体与敏感属性间的关联关系.因此,最极端和简单的隐私方法就是直接删除标识属性和准标识属性.但仅剩下敏感属性的数据表对于数据挖掘和数据发布等应用而言将变得毫无用处.因此,数据隐私保护的一般研究目标是在删除标识属性的基础上,对准标识属性进行适当的脱敏处理,以维持隐私性与可用性间的平衡.
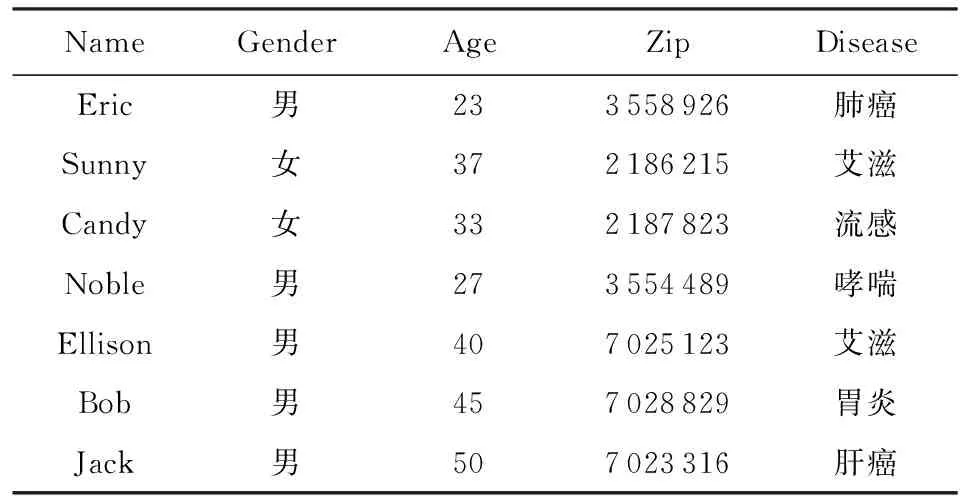
Table 1 Original Dataset表1 原始数据集
2.1 数据脱敏机制
数据共享的主要隐私保护方法是数据匿名,而泛化是数据匿名的主要手段.泛化是指将原始数据中某个准标识属性的具体值用一个更广的值域来代替.其隐私保护的思想就是通过泛化值域使得不同记录在准标识属性上不可区分,从而阻止针对具体准标识属性值的表连接.由于链接攻击依赖不同数据表间的表连接,因此k-匿名能够有效地防范表链接攻击.从保证最小化数据信息损失角度出发,我们对不同的准标识属性类型采用不同方式的泛化.
1) 数值型准标识属性.直接用等价集中各个数据属性值的最小值域来代替原始数据的属性值,实现最小泛化.例如,对于表1中的属性Age,用最小值域[23,27]代替具体的取值“23”和“27”.
2) 分类型准标识属性.各个属性值可以根据泛化层次树泛化为比原有属性值更大的最小值代替,实现最小泛化.属性值的最小泛化即为其对应的叶子节点的最小上界节点.例如,图2为疾病的泛化层次树,对于属性Disease,我们可以用含义更广的最小泛化节点“自身免疫病”代替具体的“流感”.

Fig. 2 Generalization hierarchy tree for “disease”图2 “疾病”属性的泛化层次树
数据k-匿名一般是将数据按各个记录的准标识属性相近程度划分为不同的等价集,然后对每个等价集进行泛化匿名.而聚类基本思想是将一个表数据按照相似程度划分为若干类.因此,两者自然可以相互结合.我们通过聚类来构造等价集,依此实现数据k-匿名.为了便于描述,我们给出了相关定义.
定义1.等价集.给定表数据S,若U为S中的准标识属性集合,则每个在U上取值都相近的记录集合构成一个等价集,记为Di.
定义2.等价记录.经过泛化后的等价集Di,集合中所有记录具有相同的准标识属性值,统称为等价记录,记为lDi.
定义3.k-匿名.给定表数据S和等价集D,若S中的任意D至少包括k条记录,则称S满足k-匿名.
我们以表1为例进行隐私处理:移除标识属性和其他属性,对于准标识属性进行泛化,对敏感属性不做处理.表2为2-匿名后的结果,其中包括3个等价集,每个等价集中至少包含2条记录.
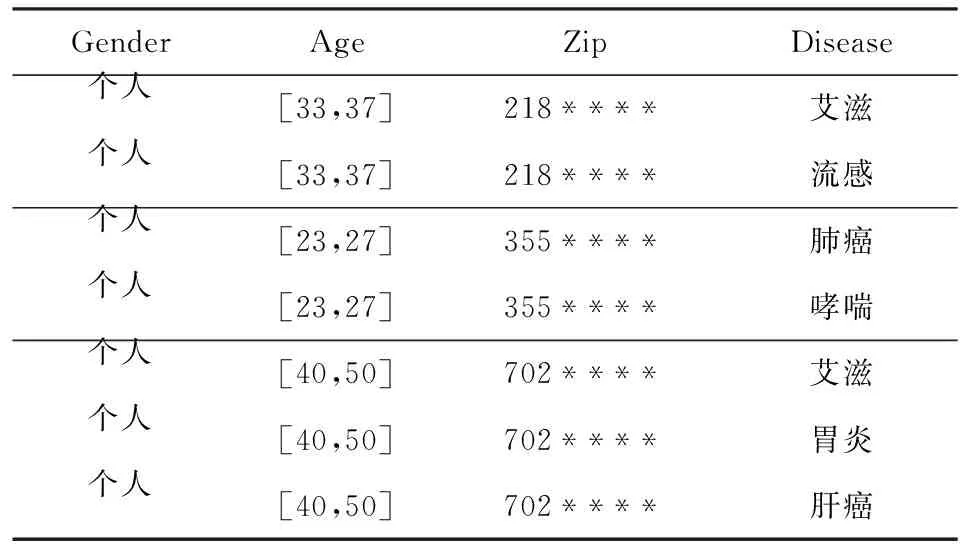
Table 2 2-anonymous Dataset表2 2-匿名数据集
如表2所示,每一行代表1条等价记录.其中,“行1,2”和“行3,4”均为1个等价集合,各包含2条等价记录;“行5,6,7”为1个等价集,包含3条等价记录.
2.2 匿名数据集的隐私保证
我们使用S表示原始表数据,S′表示匿名后的表数据.表数据中每一行记录对应1个个体,用li表示.为了保护数据的隐私,我们采用k-匿名对表数据进行隐私保护,并给出数据隐私保证的定义.
定义4.k-匿名数据隐私保护的安全性.假设S是原始表数据,采用k-匿名数据隐私保护机制对S中的准标识属性泛化处理,并成功生成匿名表数据S′.在发布S′情况下,条件成立:
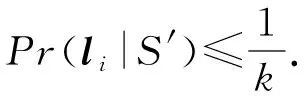
(1)
那么,就称该k-匿名数据隐私保护方案是安全的.其中,k表示用户对数据隐私保护需求,Pr(li|S′)表示攻击者从发布的匿名表数据S′中正确识别出真实记录li的概率.为了达到该目标,需要保证对于表数据S中的每一个等价集Di中记录个数都不少于k.
2.3 匿名数据集的可用性度量
为了从匿名数据集中获得有用的信息,匿名数据的信息损失必须限制在一定阈值内.由于数据分为数值型数据和分类型数据,我们针对不同的数据类型,给出了不同的信息损失度量方法[21].
1) 数值型数据的可用性度量

(2)

例如,属性Age的值域为[0,100],假设某一条记录的属性Age为40,其泛化后的取值为[40,50],则该条记录属性Age泛化后的信息损失为(50-40)/100=0.1.
2) 分类型数据的可用性度量


(3)

例如,图2中的疾病属性的泛化层次树有8个叶子节点,则|Bj|=8,若将“癌症”泛化为“后天性疾病”.而“后天性疾病”的子叶节点个数为2,则其泛化后的信息损失为1/4.
结合1)和2),我们可以计算任意表数据S在匿名处理后的数据可用性:
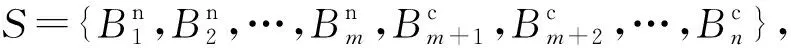

(4)
2.4 问题定义
从直观上看,用户需要的隐私泄露越少,那么获得的数据效用就越少,反之亦然.因此在基于我们的可用性度量来设计数据隐私发布机制M时,存在着隐私-可用性的平衡问题.从数据可用性来看,受隐私约束的最小信息损失是多少,以及如何设计数据发布机制来实现最小信息损失,这是一个很自然的问题.因此,本文通过目标定义来表述这个问题.
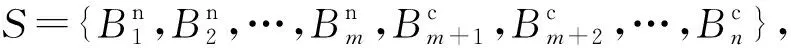
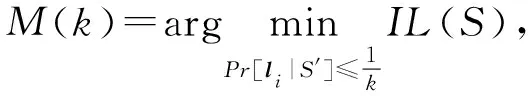
(5)
其中,IL(S)表示数据S的信息损失.
定义5提供了数据发布隐私保护框架,它包括构造等价集和泛化2个过程.具体地说,它以下面的形式来获得最优的表数据发布机制:给定原始的数据集S,通过在隐私性约束条件下达到最小信息损失来构造匿名数据集S′,然后发布匿名数据集S′.定义5将k-匿名机制的最优化问题转化为数据集的最优聚类问题,以k-匿名为约束条件,寻找信息损失最小的匿名数据集,实现最优的聚类结果.
3 基于最优聚类的k-匿名机制
3.1 总体框架
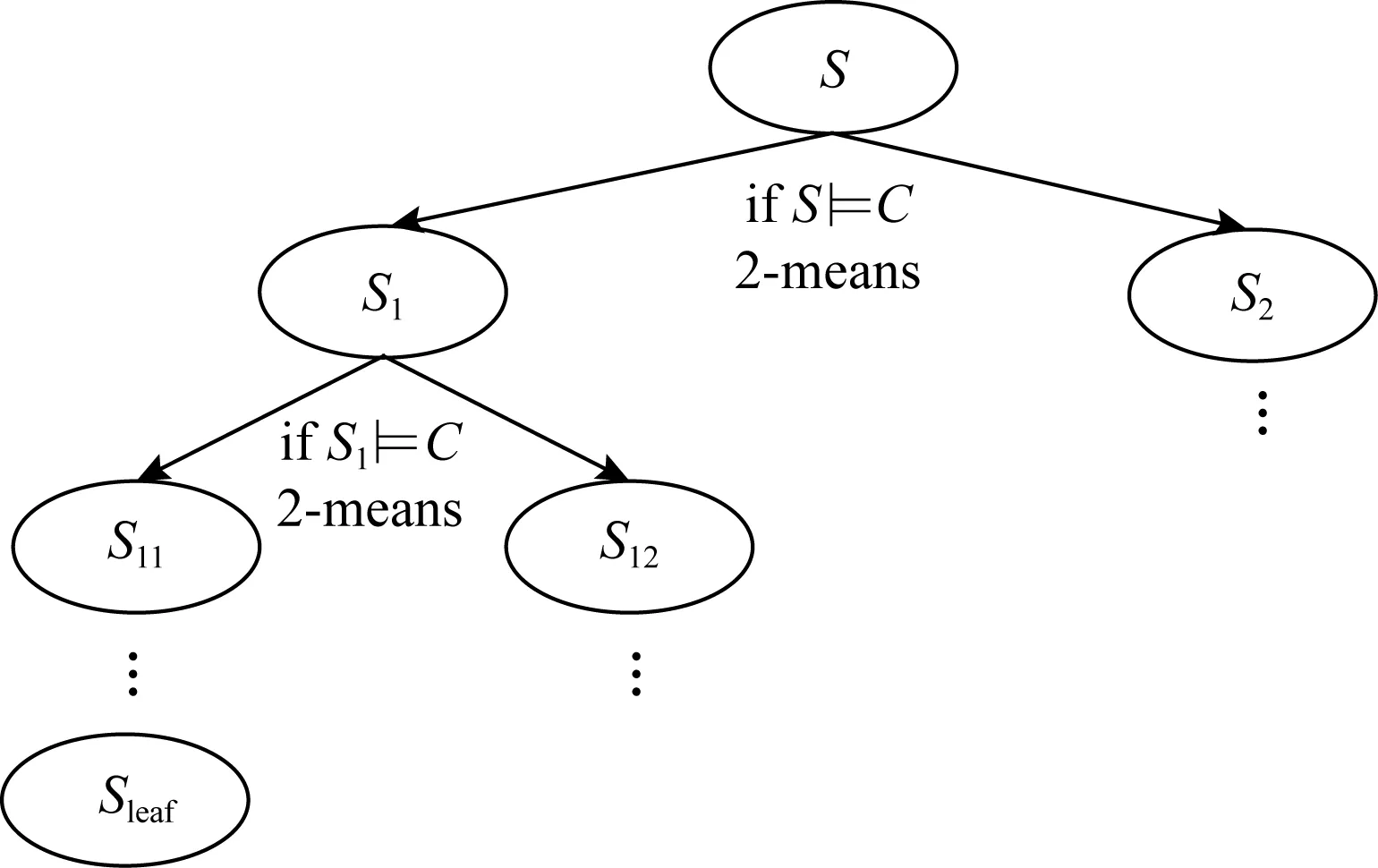
Fig. 3 k-anonymity mechanism based on optimal clustering图3 基于最优聚类的k-匿名机制
为了减少k匿名带来的数据信息损失,我们引入贪婪算法和二分机制来寻找满足k-匿名约束条件的最优聚类,实现隐私-可用性问题的最优解.总体思想如图3所示,对于待发布的数据集S,以距离最小化原则将其划分2个等价子集S1和S2,若S1和S2都满足k-匿名且两者的信息损失和小于S的信息损失,则执行该拆分步骤,否则不拆分,成为1个叶子节点Sleaf,以此迭代.我们定义二分簇的约束条件

(6)

在上述二分簇机制中,距离最小化原则可以使得各个类之内的数据最为相似,而各个类之间的数据相似度差别尽可能大,从而保证最优的聚类划分,实现最优k-匿名.此外,为了最大程度地减少数据的信息损失,我们将表数据中记录之间准标识属性的相近性与泛化后数据的信息损失结合起来,通过定义记录间的距离来反映数据泛化的信息损失大小.记录间的距离越小,它们之间的准标识属性就越相近,泛化到同一等价集后所造成的信息损失也就越小.
3.2 记录间的距离
定义6.记录间的距离.给定表数据S,S中任意2条记录la和lb在对应各个准标识属性间距离的均值定义为记录间的距离,记为dis(la,lb).
由定义6可知,记录间的距离反映了它们之间准标识属性的相似程度,由两者在各个准标识属性间的距离决定.准标识属性可分为数值型和分类型,因此,针对不同类型的准标识属性给出了不同的计算方法[16].
1) 数值型准标识属性间距离
给定表数据S,对于S中任意2条记录la和lb,假设ti为记录la和lb中第i个数值型准标识属性,则记录la和lb中数值型准标识属性ti的距离计算为
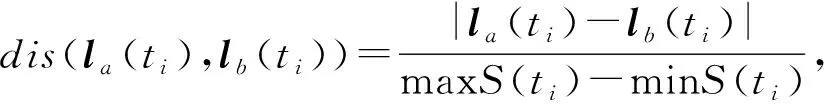
(7)
其中,|x|表示绝对值,maxS(ti)和minS(ti)分别为数值型属性ti在表数据中的最大值和最小值.
2) 分类型准标识属性间距离
给定表数据S,对于S中任意2条记录la和lb,假设tj为记录la和lb中第j个分类型准标识属性,则记录la和lb中分类型准标识属性tj的距离为
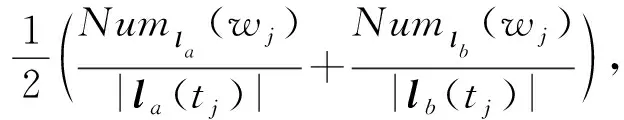
(8)
其中,|la(tj)|和|lb(tj)|分别是分类属性tj的属性值总数;Numla(wj)和Numlb(wj)分别为la和lb中wj的叶子节点个数.
结合数值型准标识属性间距离和分类型准标识属性间距离,我们可以计算任意表数据S中记录间的距离:
给定表数据S,对于S中任意2条记录la和lb,假设有n个准标识属性,其中数值型属性个数为m,分类型属性个数为n-m.ti为记录la和lb中第i个数值型准标识属性,tj为记录la和lb中第j个分类型准标识属性,则记录la和lb间的距离计算为
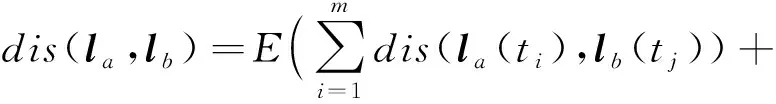
(9)
其中,E(x)为x的均值.
3.3 基于聚类优化的匿名算法
基于3.1节和3.2节的分析,本节提出一种基于聚类优化的匿名算法(clustering optimization anonymous algorithm, COAA),具体的伪代码见算法1.
算法1.基于聚类优化的匿名算法COAA(S,k).
输入:数据集S、匿名参数k;
输出:匿名数据集S′.
① 对S中所有的准标识属性进行最小泛化;
②ζ1,ζ2←newCore(S);
/*寻找2个新核心*/
③S1←{ζ1},S2←{ζ2};
④ for eachli∈S/*2-聚类*/
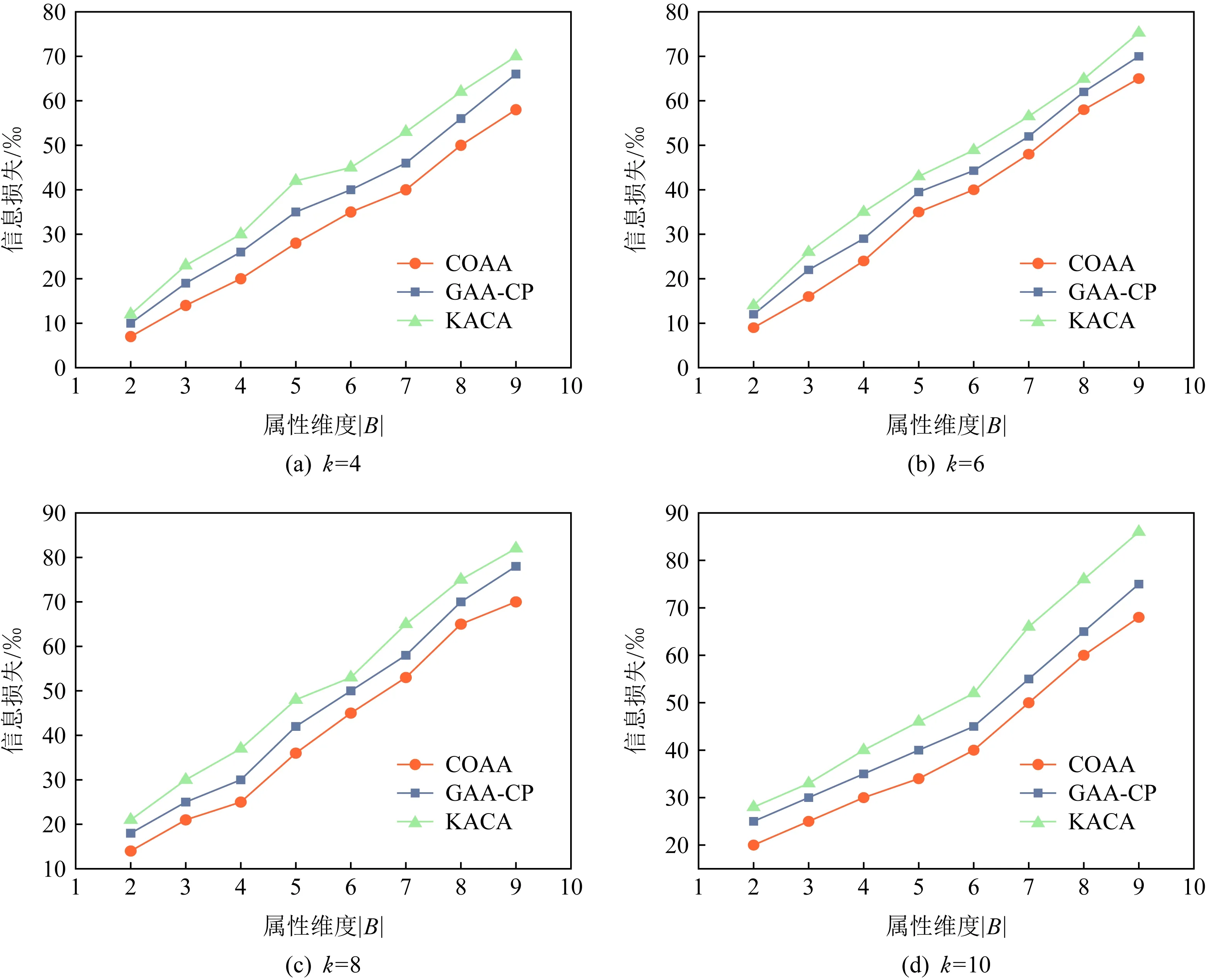
⑤ ifdis(li,ζ1) ⑥S1←S1+{li}; ⑦ else ⑧S2←S2+{li}; ⑨ end if ⑩ end for |S1|>kand |S2|>k) 在算法1中,先将数据集中所有记录看成一个等价集,对等价中所有的数据属性进行最小泛化;然后,在等价集中选取距离最远的2条记录ζ1和ζ2作为新等价子集的中心,计算各条记录与等价集中心之间的距离,并以距离最小化原则将S划分为S1和S2;最后,判断|S1|与|S2|中记录的个数是否大于k,且它们的信息损失总和小于S的信息损失.如果是,则迭代此划分过程;否则迭代终止.该聚类划分方法可以使得各个类之内的数据最为相似,而各个类之间的数据相似度差别尽可能大,保证最优的聚类划分,实现最优k-匿名. 定理1.不同记录准标识属性间的距离与这2个属性泛化后的信息损失成正比. 证明.假设2条记录为la和lb.记录间的准标识属性分为数值型准标识属性和分类型准标识属性. 1) 数值型准标识属性 假设数值型属性ti泛化为[pi,qi],则它们泛化后的信息损失为 (10) 由于la(ti)和lb(ti)之间的距离为 (11) 则有 (12) 2) 分类型准标识属性 假设分类型属性tj泛化为wj,那么记录la,lb在分类属性Bj上泛化后的信息损失定义为 (13) 由于la(tj)和lb(tj)之间的距离为 (14) 则有 (15) 由此可得无论是数值型准标识属性还是分类型准标识属性,它们之间的距离与泛化后的信息损失成正比.因此,定理1成立. 证毕. 定理2.根据准标识属性间距离最小原则,构造满足k匿名的最优等价类,能够保证生成的等价类具有最小泛化信息损失值. 证明.由定理1可知,数据的信息损失和数据间距离成正比,通过最小距离进行聚类划分来实现k-匿名最优等价集,进而可以保证信息损失达到最小. 证毕. 定理3.COAA算法能找到最优解. 证明. 我们把本文COAA算法记为A,其解记为RA.如果算法A不是最优的,那么就一定存在其他最优算法.假设RB是和RA最相近的一个最优算法解.其中,“最相近”是指算法B和算法A生成的前k-1个叶子集都相同,从第k个开始不同. 综上所述,我们找到了一个最优解RB′,它和RA具有共同叶子集个数有k个,这和我们前提假设最多有k-1个相同相矛盾,所以,算法A是最优的. 证毕. 在COAA算法中,对聚类后的数据进行泛化处理,其本质是对一定范围内的数据进行匿名处理,以区域值代替具体的取值,故泛化处理后的数据取值相同,进而攻击者不能猜测出具体的数据.COAA算法主要分为等价集划分和泛化匿名2个阶段.在等价集划分阶段,保证每一个等价集的记录个数都大于等于k.在泛化匿名阶段,保证同一等价集中各个记录的准标识属性取值相同.因此,在匿名数据集S′中任取一条等价记录lDi,至少存在k-1条其他记录,并且它们具有相同的准标识属性值.显然,匿名数据表S′满足k-匿名,能够有效抵制链接攻击,有效保护数据隐私. Fig. 4 How the information loss changes with |B| when k is constant图4 k值固定时数据信息丢失随属性维数|B|的变化规律 本节通过实验分析验证COAA算法的性能,并且将COAA算法与文献[12]提出的KACA算法和文献[16]中提出的GAA-CP算法进行比较.本实验所采用的数据来源于机器学习数据库中的Adult数据集(AD-data),保留了其中2 000个记录的表数据.本文与文献[16]一样,每一条记录都保留了Age,Gender,Education,Marital Status,Race,Work Class,Native Country,Salary Class,Occupation这9个数据属性,其中Occupation为敏感属性.实验环境为:Intel®CoreTMi5-3470U CPU@3.20 GHz 2.40 GHz;4 GB(RAM)内存;Windows 10专业版64位操作系统,基于X64的处理器;算法均采用MATLAB R2019a实现.考虑到实验误差的影响,每组实验重复进行5次,结果取平均值. 为了分析数据信息损失度随属性维度|B|、匿名参数k和不同数据集大小的变化规律,我们进行了以下实验. Fig. 5 How the information loss changes with k when |B| is constant图5 属性维度|B|固定时数据信息损失随k值的变化规律 1) 研究了不同的匿名k值对数据信息损失度的影响.图4(a)~4(d)给出了当k=4,6,8,10时,COAA算法、GAA-CP算法和KACA算法中数据属性维度的变化对数据信息损失量大小的影响.从图4中可以看到,随着匿名参数k值的增大,3种算法下表数据的信息损失度也在不断增大.这是由于随着k值的增大,等价集中记录的个数增加,将这些记录进行泛化为同一属性值时,需要增大泛化程度,这样各记录数据的信息损失度将会增大,进而总体的信息损失度也会增大.而且从图4中可以发现,始终有IL(COAA) 2) 研究了对于同一个数据属性维度|B|,不同的匿名k值对数据信息损失度的影响.图5给出了当|B|=3,5,7,9时,COAA算法、GAA-CP算法和KACA算法中匿名参数k值的变化对数据信息损失量大小.从图5中可以看出,对于同一个|B|值,随着匿名参数k值的增大,信息损失度也在不断增大.这是由于随着k值的增大,等价集中的元组的记录个数增加,将这些记录进行泛化时,需要增大泛化程度,这样各记录数据的信息损失度将会增大,进而总体的信息损失度也会增大. 3) 研究了在k=6,|B|=7时,不同数据集大小对数据信息损失度的影响.图6给出COAA算法、GAA-CP算法和KACA算法中数据集大小的变化对数据信息损失量的影响.从图6中可以看出,随着数据个数的增加,3种模型的信息损失度都在不断增大.这是由于匿名化操作的数据个数增加,需要处理的数据属性值也会增加,进而导致信息损失变大.而且从图6可以发现,对于不同大小的数据集,本文所提的COAA算法的信息损失小于GAA-CP算法和KACA算法. Fig. 6 The change for information loss with different data sets图6 信息损失随不同数据集大小的变化规律 图7和图8分别给出了COAA算法、GAA-CP算法和KACA算法随不同的匿名参数k以及不同数据集下的执行时间的比较.从图8可以看出,当k值发送变化时,其执行时间也相应改变.随着k值的增大,执行时间也在不断增加.这是因为k值增大,等价集中记录的个数增加,泛化所需要的时间变长,进而执行时间变长.在图8中,我们设置了k=6,7的情况下执行时间随着数据集大小的变化规律,可以发现,随着数据集的增大,运行时间逐渐增加,这是由于数据集变大,相应的等价集数量增加,进而在泛化时所需要的时间也相应变长.并且在图7和图8中,COAA算法的执行时间相比GAA-CP算法和KACA算法,执行时间总是最短.原因是:本文方法对数据进行聚类划分时始终采取二分法机制,在满足可用性约束条件下进行聚类划分.由于我们聚类划分的截止条件为2点:1)满足等价集中记录个数不少于k;2)划分后子集合的信息损失(可用性)小于划分前集合的信息损失,约束条件比其他2种算法更严格,所以聚类划分次数相比其他2种算法较少,即执行时间更短. Fig. 7 Running time with different k values图7 不同k值下的执行时间 Fig. 8 Running time with different data sets图8 不同数据集大小下的执行时间 基于聚类的k-匿名机制是当前数据隐私保护的主要方法,它能有效防范针对隐私的背景攻击和链接攻击.为了解决基于聚类的k-匿名机制中可用性和隐私性的平衡问题,本文提出了一种基于贪心算法和二分聚类思想的最优k-匿名数据隐私保护机制.选取表数据中最远的2条记录作为聚类中心,然后按照k-匿名约束对数据集进行迭代2-聚类划分,尽可能使得各个类之内的数据最为相似,从而保证了在满足隐私需求条件下聚类的信息损失总量最小,即解决了k-匿名约束条件下的可用性最优问题.实验结果表明,在相同隐私约束的条件下,本文方案展示了最小的信息损失.此外,当数据之间相似性增大时,它在隐私和可用性权衡方面的优势将会变得更大.我们还展示了本文方案的效率,发现本文方案数据匿名时间明显优于其他匿名方案. 作者贡献声明:张强负责方案的讨论、性能分析以及论文撰写;叶阿勇指导方案的拟定和整体设计,把握论文创新性,并审阅修订论文;叶帼华参与论文方案可行性讨论与分析;邓慧娜参与论文图表设计与规划;陈爱民参与论文公式与论文文字校对.4 算法分析
4.1 有效性分析

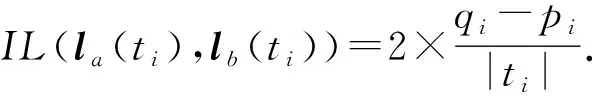
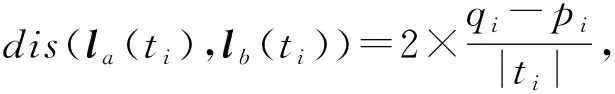
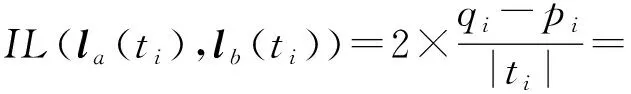
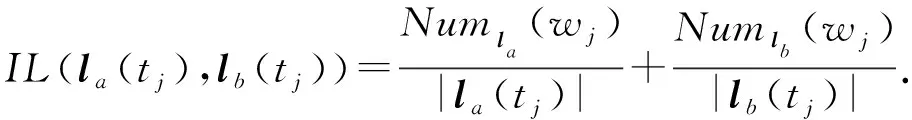
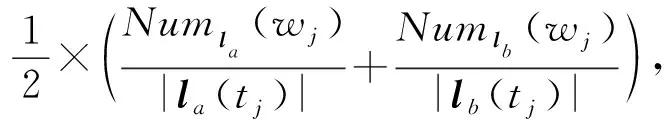

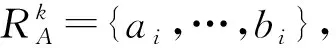
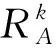
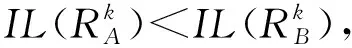
4.2 安全性分析
5 实验与结果分析
5.1 信息损失比较
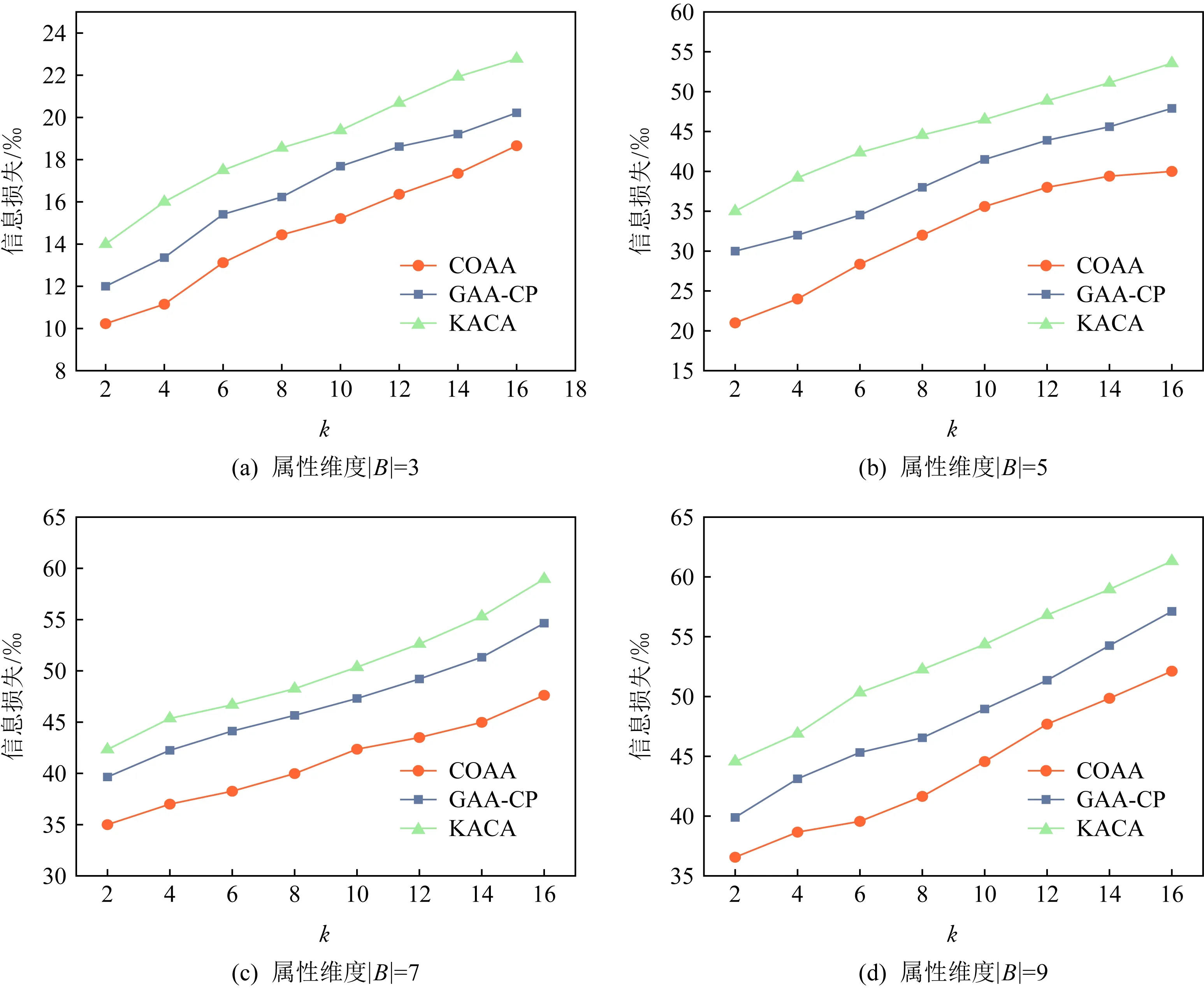
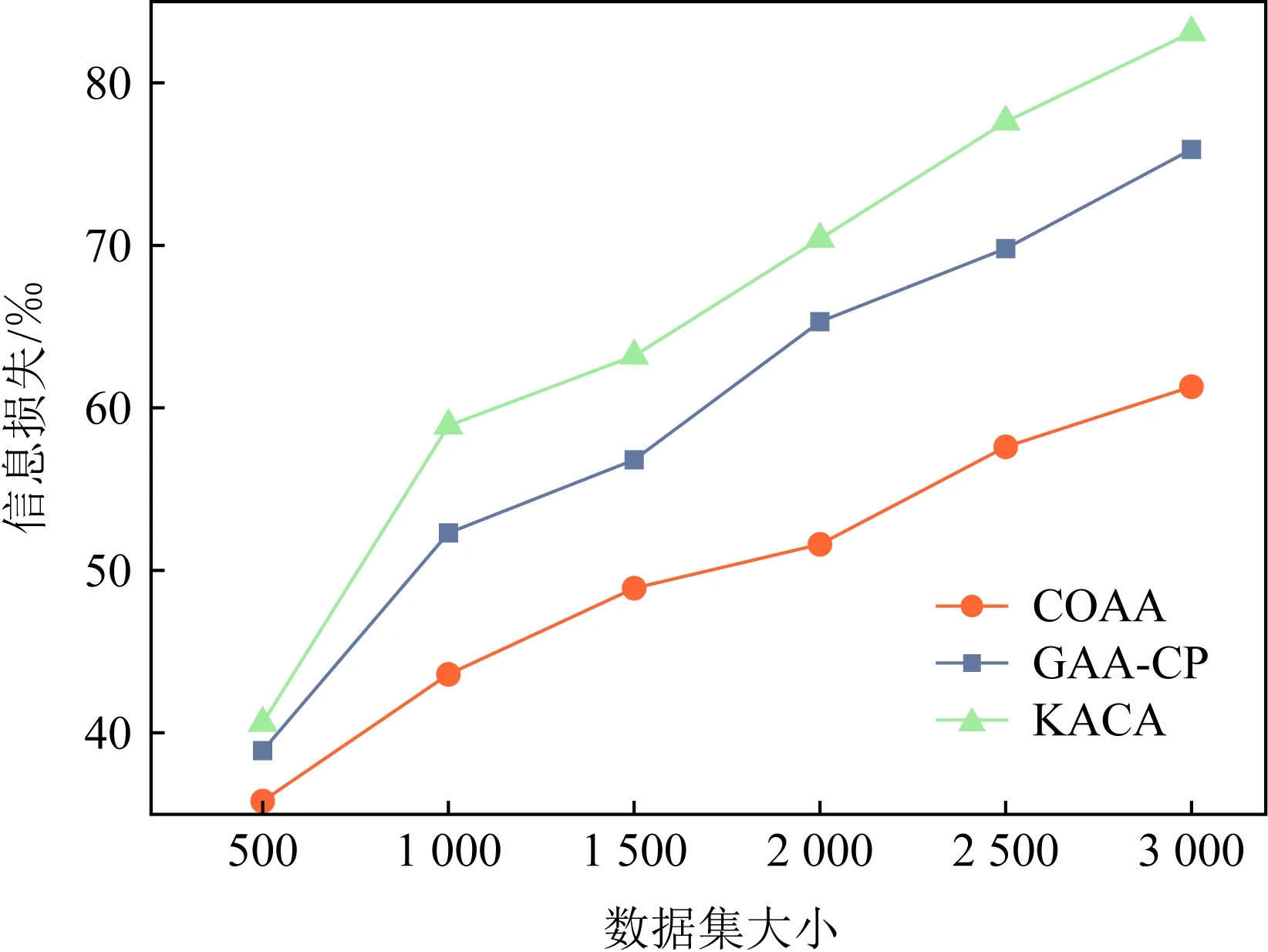
5.2 执行时间比较
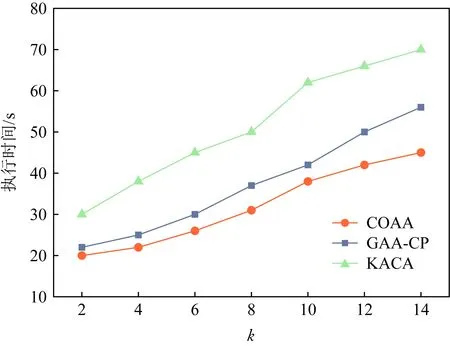
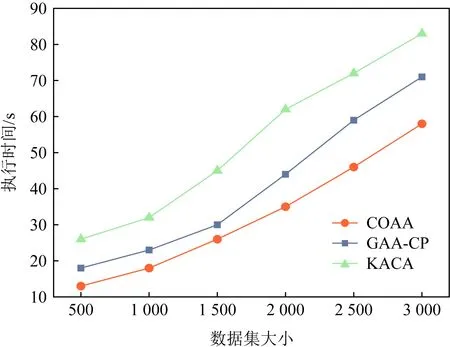
6 总 结
