射孔过程中井筒力学响应与完整性失效研究*
2022-07-12闫炎管志川阎卫军许玉强
闫炎 管志川 阎卫军 许玉强
(1.太原理工大学原位改性采矿教育部重点实验室 2.中国石油大学(华东)石油工程学院 3.中国石油长城钻探工程有限公司)
0 引 言
射孔完井作为一种重要的油气井完井方式,是影响储层最终采收率的关键因素[1-3]。随着页岩气、煤层气等非常规油气开发程度逐渐提高,水平井体积压裂技术得到了大规模的应用与发展。在压裂开发过程中,一旦井筒密封完整性遭到破坏,地层中的流体极易进入井筒环空,诱发环空窜流[4-6],进而影响油气井产量,缩短油气井服役寿命。而井筒密封完整性的破坏形式主要表现为固井水泥环的破坏与固井界面微环隙的产生。目前,压裂中井筒失封的研究主要集中在循环加载后水泥环的破坏或界面脱黏产生微环隙,而射孔对井筒密封完整性的破坏并未引起重视。当射孔弹起爆后,大量的爆生气体在井筒内形成压力波,对井筒形成挤压,使井筒受到的应力急剧增大,从而大大增加了水泥环密封失效的风险。
射孔弹的型号与结构是影响聚能射流侵彻性能(孔径、穿深)的重要因素。目前针对射孔弹在靶体中穿深的研究[7-9]目的在于改善储层流体进入井筒中的流动阻力,提高储层采收率。而射孔在形成孔道的同时也对井筒造成了不可逆的损伤[10-12]。W.K.GODFREY[13]开展了室内射孔试验,研究了聚能射流对于套管/水泥环界面胶结强度的影响,结果显示低强度水泥与套管的胶结强度会在射孔后显著降低,而高强度水泥与套管的胶结强度在射孔后降低程度有限,但对此并未从力学机理上给予解释。YAN Y.等[14]前期通过环形靶射孔试验证实了射孔后固井界面的脱黏现象,但射孔过程中水泥环本体的力学响应与破坏情况并未引起关注。
本文结合现场有枪身射孔方式,基于LS-DYNA有限元计算平台,利用数值计算的方法模拟井下射孔过程,对射孔过程中套管、水泥环的应力响应与破坏特征进行分析;开展了柱形靶侵彻试验,验证了数值模拟方法的可靠性;还分析了射孔弹药量、水泥剪切模量、地层围压对射孔过程中水泥环应力响应的影响规律。所得结论为油气井射孔施工优化与压裂前井筒完整性预测提供了理论支持。
1 射孔弹侵彻井筒模型
1.1 几何模型
在射孔完井作业过程中,射孔弹固定在射孔枪的弹架上,聚能射孔弹起爆后,射孔弹药型罩在炸药推动下形成聚能射流并对井筒形成侵彻。图1为油井常用DP36RDX25型聚能射孔弹[15]示意图。射孔弹主要由药型罩、炸药与弹壳组成。药型罩开口直径36 mm,锥角为46°,药型罩为等壁厚结构,壁厚为1.5 mm。药型罩材质为紫铜,壳体材质为45号钢,射孔弹装药为黑索金炸药。射孔弹的起爆方式为中心点起爆。由于聚能射流侵彻井筒与岩层是一个高温、高压、高应变率的过程,这给计算带来了相当的难度。为建立射孔侵彻计算模型,假设:①水泥、砂岩为各向同性无黏材料,不考虑其非均质性;②聚能射流为轴对称流动,且射孔弹中心线与井筒内壁面垂直。基于以上假设,建立物理模型,如图2所示。为减少模型计算量,混凝土靶外径设置为50 cm,靶体高度设置为15 cm。

图1 油井聚能射孔弹几何结构Fig.1 Geometric structure of shaped charge for oil wells

图2 射孔弹侵彻井筒的物理模型Fig.2 Physical model of shaped charge penetrating wellbore
为了消除冲击波反射对井筒内部应力分布造成的干扰,在环形靶的上、下底面以及地层外侧边界施加无反射边界条件。模型中套管外壁面与水泥环内壁面、水泥环外壁面与地层内壁面应保持共面以模拟套管/水泥环界面与水泥环/地层界面的胶结。此外,模型中的网格均为结构化网格,并在井筒与地层沿射孔方向30°方位内进行网格加密。
1.2 控制方程与参数
数值模型中涉及的材料较多,下面针对各材料的控制方程做简要介绍。
射孔弹内有炸药,本文采用基于Chapman-Jouguet理论的高能燃烧模型[16]来描述炸药的起爆过程。高能燃烧模型定义爆炸产物压力p如式(1)所示。
p=Fps(υ,E)
(1)
式中:ps为根据产物状态方程计算得到的压力,MPa;F为燃烧系数;E为单位体积炸药爆炸内能,J/m3;υ=1/ρ为爆炸产物相对体积,m3/kg;ρ为爆炸产物密度,kg/cm3。
炸药爆炸后的压力由“Jones-Wilkins-Lee”(JWL)方程描述,JWL的表达式如下[17]:
(2)
式中:A、B、R1、R2、ω为炸药材料参数,取值分别为3.710、0.074、4.150、0.950及0.300。
药型罩在炸药起爆后形成熔融态的金属射流,在此过程中,药型罩瞬间发生巨大形变,因此材料模型选用适用于描述大应变、高应变率、高温环境下金属材料的Steinberg-Guinan模型[18]。根据Steinberg-Guinan本构模型,药型罩融化前剪切模量G定义如式(3)所示。
(3)
药型罩的屈服强度σy为:
(4)

(5)
式中:x为剩余相对体积,m3/kg,x=1-V;Tm0为初始融化温度,K,取值为1 356 K;γ0为Mie-Gruneisen状态方程的一个常数。
用于描述药型罩的Mie-Gruneisen状态方程为:
(γo+aμ)E
(6)
式中:C为剪切-压缩波速度曲线的截距,m/s,取值为3 920 m/s;S1、S2和S3是剪切-压缩波速度曲线的斜率系数,取值为1.49;μ为参变量,μ=ρ/ρ0-1,其中ρ0为正常状态下的介质密度,kg/m3,紫铜药型罩取值8.9×103kg/m3;ρ为介质压缩后的密度,kg/m3;a是γ0与μ的一阶体积修正量。
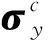
(7)

射孔枪与套管的材料参数根据API标准[19-20]选择,各项力学参数如表1所示。

表1 套管与射孔枪的材料参数Table 1 Material parameters of casing and perforating gun
由于Holmquist-Johnson-Cook模型[21]能够很好地描述工程材料在大应变、高静水压力和高应变率下的动态力学行为,所以在工程材料冲击爆炸问题的数值分析中得到广泛应用。由于水泥基混凝土材料的力学性质均较为相近,所以采用HJC(Holmquist-Johnson-Cook)模型描述水泥环与砂岩靶,模型中屈服面方程为:
(8)

(9)

HJC模型的状态方程用于描述静水压力和体积应变之间的关系,分为弹性压缩、压实变形和密实后变形三个阶段。
第一阶段为线弹性区,静水压力和体积应变呈线性关系,即:
p=Keμγ(-T(1-D)≤p≤pcrush)
(10)
式中:Ke为弹性体积模量,GPa;μγ为体积应变;pcrush为压实静水压力,MPa。
第二阶段为过渡区,此时材料内的空洞逐渐被压缩从而产生塑性变形,加载和卸载方程如下:
(11)
式中:μcrush为压实静水压力下对应的体积应变;plock为压实压力,MPa;μplock为压实压力处的体积应变;μ0为卸载前的体积应变;p0为μ0对应的静水压力,MPa。
第三阶段为无气孔密实区,这一阶段材料已完全破碎,加载和卸载方程分别为:
(12)
式中:K1、K2和K3为材料常数。水泥石的部分材料参数根据API标准中G级油井水泥[22]标准确定。
表2为水泥与砂岩的材料参数。

表2 水泥与砂岩材料参数Table 2 Material parameters of cement and sandstone
1.3 套管-水泥环破坏判别标准
为说明射孔过程中套管、水泥环是否发生破坏,需要采用合理的破坏准则与参考指标来进行判定。套管采用基于第四强度理论的Mises应力来判断是否发生屈服破坏。水泥环则选取最大拉应力准则与莫尔-库仑失效准则作为拉伸破坏与剪切破坏的破坏准则,其表达式分别为:
σ≥σt
(13)
(14)
式中:σ为水泥内部应力,MPa;σt为水泥石抗拉强度极限值,MPa;τ0为水泥石内聚力,MPa;ψ为内摩擦角,(°);σ1与σ3分别为水泥石最大主应力与最小主应力,MPa。
2 柱形靶射孔侵彻试验
2.1 试验装置与流程
柱形靶侵彻试验如图3所示。图3a为ø400 mm射孔装置结构图。试验装置由三轴高压釜、液压动力泵组及伺服控制系统等组成[23]。试验中,用P110钢板模拟同材质套管,用普通硅酸盐水泥模拟固井水泥,用砂岩靶模拟地层。其中:钢板厚度为0.78 cm,水泥环厚度为3 cm,砂岩靶长度为76 cm,钢板、水泥、砂岩靶直径均为120 mm。试验中共用4种射孔弹型号,分别为DP32RDX16、DP36RDX25、DP41RDX32和DP44RDX38。试验所用G级油井水泥浆的水灰比为0.44,浆体密度为1.82 g/cm3,养护28 d后单轴抗拉强度与单轴抗压强度分别为3.3和34.0 MPa。

图3 射孔试验装置Fig.3 Perforation test
将预先制成的砂岩靶、水泥环、钢板依次放入靶套中,将靶套上好螺丝和圈套并加固,完成靶体的装配。然后将射孔弹安装在射孔器中,并接好雷管。最后将射孔组件利用吊钩,放入地下高温高压容器中,并由控制装置进行加压和点火射孔。试验结束后破开砂岩靶,观测射孔弹在靶体中形成的锥形孔道,如图3b所示,统计不同型号射孔弹在靶体中的平均穿深。
2.2 结果对比
图4为不同型号射孔弹穿深的数值计算结果与试验测量结果对比。从图4可知,不同型号射孔弹穿深的计算误差均小于5%,说明该计算方法可以较为准确地模拟油气井射孔过程。由于本文重点关注射孔过程套管和水泥环的应力变化规律与破坏特征,所以下文将分析射孔过程中套管与水泥环的应力响应特征,以判断其破坏类型及对井筒密封完整性的影响。

图4 不同型号射孔弹穿深的数值结果与试验测量结果对比Fig.4 Comparison of penetration length between numerical and experimental results for different types of shaped charge
3 结果分析
取孔眼所在中心截面内方位角α为8°、12°、16°和20°处(以孔道中心轴线为起始方位)套管内外壁面的8个测点,可得射孔过程中各测点Mises应力变化规律,如图5所示。从图5a可以看出:射孔弹起爆后套管Mises应力在40 μs内迅速增大,随后振荡波动;160~240 μs套管内外壁面的Mises应力出现峰值,且峰值随着方位角的增大逐渐降低。图5b为射孔过程中不同时刻孔眼所在中心截面内套管Mises应力分布曲线。从图5可知,射孔过程中套管内壁面的应力集中现象比外壁面更加明显。此过程中各测点峰值均小于套管屈服强度,因此,射孔过程中孔眼周围的套管并未发生屈服破坏。
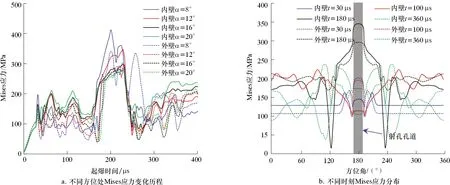
图5 射孔过程中套管Mises应力变化规律Fig.5 Changes of Mises stress on casing during perforation
射孔过程中水泥环在上述4个方位8个测点处的轴向拉应力变化规律如图6所示。由图6a可以看出,水泥环一界面上的4个测点处的最大拉应力均超过抗拉强度,即水泥环在上述位置均发生拉伸破坏,水泥环二界面处仅在α=8°处发生拉伸破坏。图6b为射孔过程中不同时刻孔眼所在中心截面内水泥环沿井筒轴向拉应力分布曲线,射孔过程中水泥环的拉伸破坏主要集中在锥角为60°的锥体范围内。射孔过程中水泥环在上述8个测点处的剪切应力变化规律如图7所示。由图7a可知,水泥环一界面上的4个测点处剪切应力均超过水泥石内聚力,即水泥环在上述位置均发生剪切破坏,而水泥环二界面不会发生剪切破坏。由图7b可知,射孔过程中水泥环的剪切破坏同样主要集中在锥角为60°的锥体范围内。由于射孔过程中水泥环一界面α=8°处的应力峰值最高,故在影响因素分析中,选取此位置的测点进行射孔过程中水泥环应力变化规律的敏感性分析。
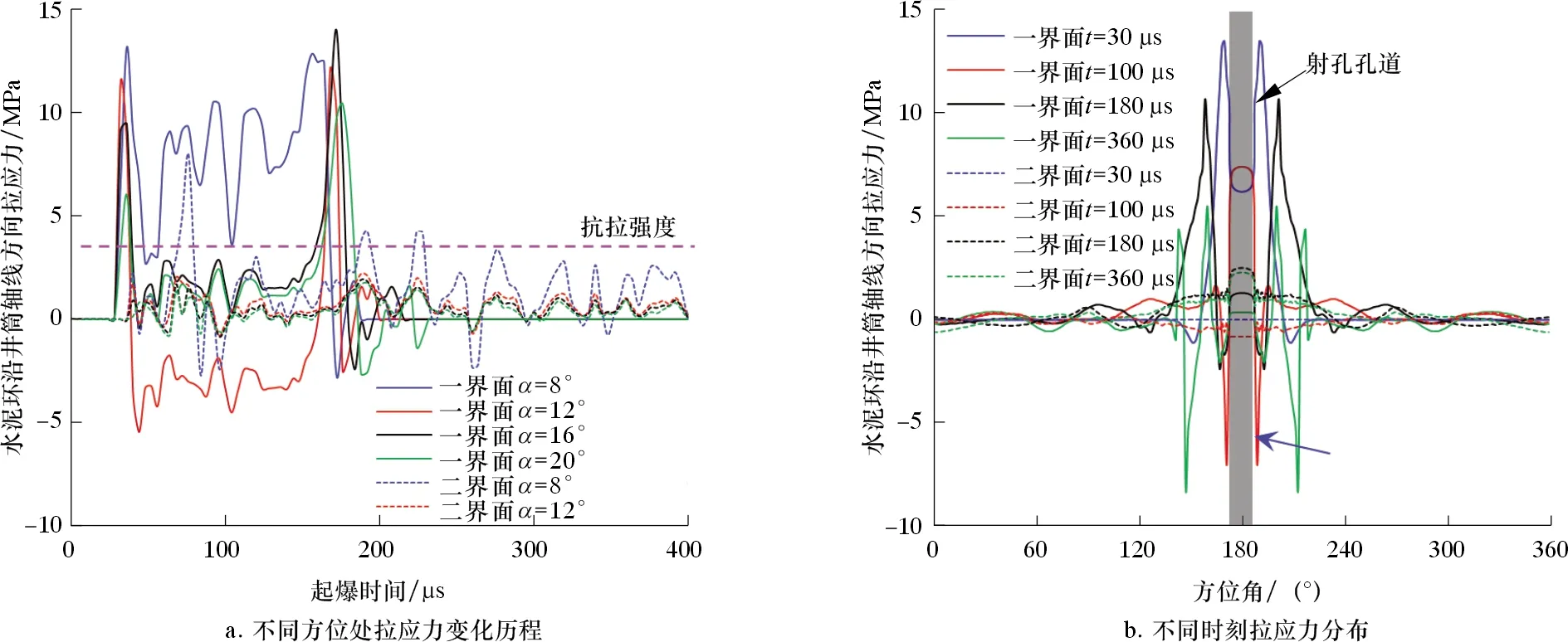
图6 射孔过程中水泥环井筒轴线方向拉应力变化规律Fig.6 Changes of tensile stress on cement sheath in the axial direction of wellbore during perforation
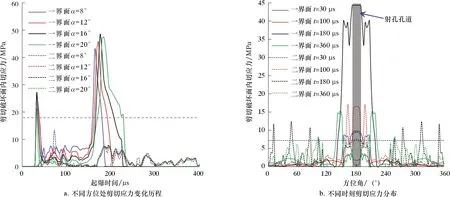
图7 射孔过程中水泥环剪切应力变化规律Fig.7 Changes of shear stress on cement sheath during perforation
4 影响因素
4.1 射孔弹装药量
射孔弹炸药的装药量是聚能射流侵彻性能的重要影响因素之一[24-25]。图8为不同射孔弹药量下水泥环应力响应规律。由图8可知,射孔弹装药量的增加不仅增大了水泥环射孔过程中的拉应力与剪切应力的峰值,同时还缩短了应力峰值到达的时间。这是由于装药量的增加提高了聚能射流头部的侵彻速度,从而使射孔过程中水泥环受到的冲击载荷更大。三种装药量下的射孔弹侵彻后,水泥环均出现了拉伸破坏与剪切破坏,即低药量射孔弹并不能避免孔眼周围水泥环的破坏。

图8 射孔弹装药量对水泥环应力响应的影响规律Fig.8 Influence of perforating charge load on stress response of cement sheath
4.2 水泥剪切模量
水泥剪切模量对射孔过程中自身的应力响应必然存在影响。图9为不同水泥剪切模量下射孔过程水泥环应力响应规律。由图9可知,剪切模量的升高降低了水泥环射孔过程中的拉应力与剪切应力的峰值,但仍然难以避免孔眼附近水泥环的拉伸破坏与剪切破坏。现场为了提高水泥环的封固能力往往采用增韧水泥浆进行固井,增韧水泥降低了水泥的剪切模量(降低弹性模量,增大泊松比)[26-27],增大了孔眼附近水泥环的破坏风险。

图9 水泥剪切模量对水泥环应力响应的影响规律Fig.9 Influence of cement shear modulus on stress response of cement sheath
4.3 地层围压
地层围压对水泥环内应力状态的分布有显著影响。图10为不同地层围压下射孔过程水泥环应力响应规律。由图10可知,随着地层围压增加,增大了聚能射流侵彻初期水泥环井筒轴向拉应力的峰值,但明显降低了聚能射流侵彻初期水泥环孔眼周围的剪切应力,这表明围压的增加并不能改善射孔过程中水泥环的完整性,反而增加了水泥环的失封风险。
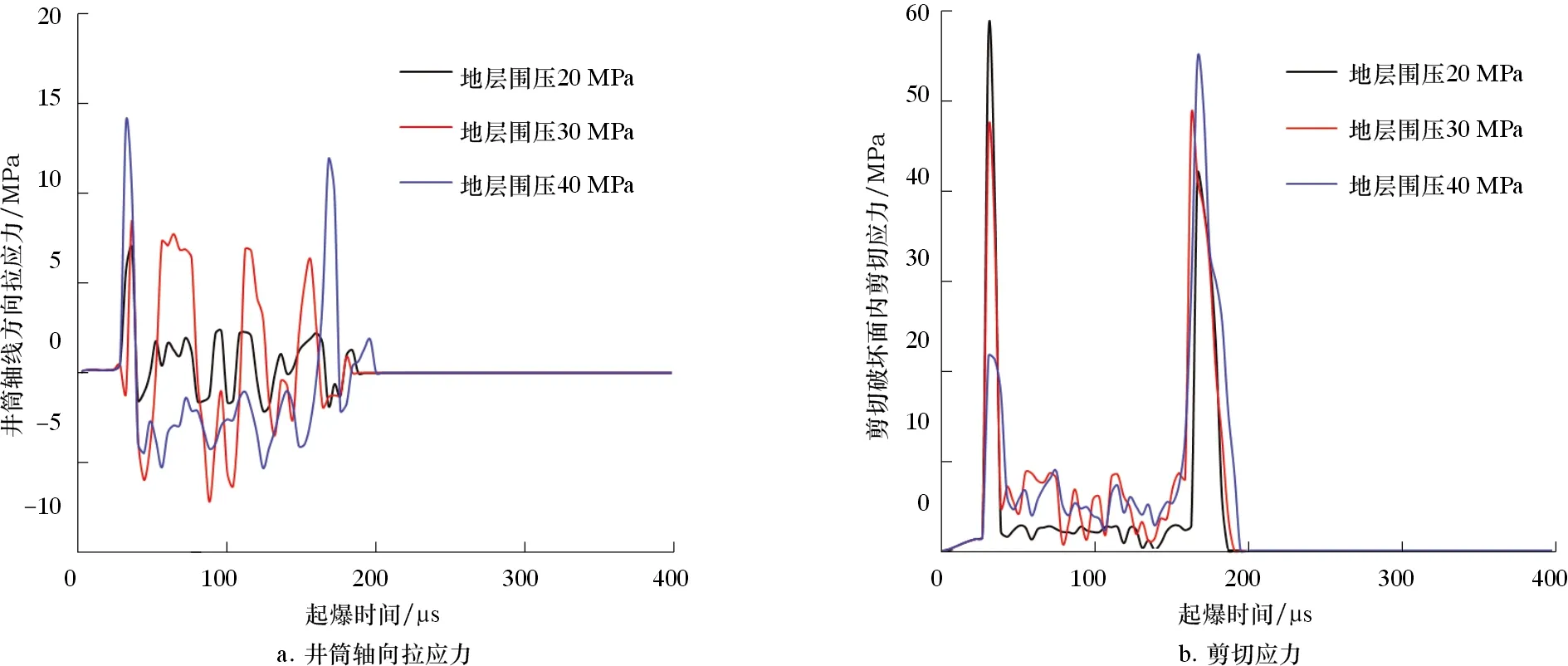
图10 地层围压对水泥环应力响应的影响规律Fig.10 Influence of formation confining pressure on stress response of cement sheath
5 结 论
(1)建立了聚能射流对于井筒的侵彻计算方法,该方法可用于定量分析射孔过程中井筒的应力响应规律。通过将计算的射孔弹穿深与侵彻试验结果进行对比,验证了模型的可靠性。
(2)射孔弹侵彻井筒的过程中套管不会发生屈服破坏,水泥环一界面将发生拉伸与剪切破坏,水泥环二界面仅在靠近孔眼处发生拉伸破坏。射孔过程中水泥环的拉伸与剪切破坏主要集中在锥角为60°的锥体范围内。
(3)大药量射孔弹、低剪切模量水泥环与高地层围压增大了射孔过程中水泥环的应力峰值,增加了射孔过程中水泥环的破坏风险。但这三个参数无论如何改变,都难以避免水泥环在射孔后局部范围的密封失效。
