基于变风向高斯烟团混合模型的污染物扩散研究
2022-07-11黄淑龙毛亮李洪辉张冰焘孟子贺武海花
黄淑龙, 毛亮, 李洪辉*, 张冰焘, 孟子贺, 武海花
(1.中国辐射防护研究院, 太原 030006; 2.中核高放废物地质处置评价技术重点实验室, 太原 030006)
环保与安全对工业技术的发展和应用起着决定性的作用。化工、电力、交通等行业的设施在运行过程中会产生大量气态污染物,在突发事故时可能会造成严重的污染物泄漏,通过大气扩散在短时间内对周边环境产生影响[1]。因此,需要开展气态污染物的大气扩散研究,实时预测气态污染物在大气中浓度分布,为制定应急响应计划和开展响应行动提供技术支持。
目前污染物大气扩散的数值模拟模式主要有:高斯模式、拉格朗日模式、欧拉模式、计算流体力学(computational fluid dynamics,CFD)模式以及拉格朗日-欧拉嵌套模式5类,其中高斯模型一般适用于核事故早期较短时间且近距离范围内的模拟,能够迅速确定放射性核素扩散的大致方向,采取应急措施[2]。Hyojoon等[3]开展了放射性核素的大气扩散模拟,并通过野外示踪实验证了高斯烟羽模型应用于核电厂环境影响评价的有效性。Elkhatib等[4]采用高斯烟羽模型对放射性同位素生产设施的泄漏情况开展了模拟,分析了环境中气载放射性物质的扩散和沉积过程,评估了泄漏事故对公众产生的辐射影响。Cao等[5]以高斯烟羽模型为基础,采用Fortran语言编写了放射性核素大气扩散计算程序RADC,分析了模型的不确定性,计算了观测误差的影响。对于非放射性污染物扩散,徐晓波[6]利用高斯模型研究了关中地区的SO2扩散,并对影响扩散的因素进行了灵敏度分析。Liu等[7]采用地面反射系数和修正高度改进了高斯烟羽模型,采用反演计算方法预测污染物的泄漏点和浓度。徐路程等[8]运用高斯烟羽模型模拟了烟幕在大气中的扩散效果,分析了平均风速和风速标准差对烟幕扩散的影响规律。李冰晶等[9]、赵锐等[10]、彭星煜等[11]采用高斯模型分别研究了化工企业硫化氢、液氨、天然气的泄漏扩散事故。但上述研究重点关注于污染物扩散稳定后的影响范围和影响程度,对污染物的实时扩散过程和扩散发展情况研究较少。史宝军等[12]针对液化石油气泄漏扩散问题,采用引入时间参数的高斯烟羽混合模型,解决了高斯烟羽模型不能计算泄漏早期随时间变化的浓度分布问题。但未考虑风向对空间浓度分布的影响。李悦等[13-14]基于SLAB模型标准模式,通过时间单元划分和坐标系旋转平移的方式提出了适用于变化风向风速条件下的危险气体扩散计算方法。基于此,结合史宝军等[12]、李悦等[13]的研究思路,对高斯烟团模型进行改进。
为了实时预测气态污染物在大气中的浓度分布,基于Python语言,利用时间分段处理和坐标转换的方法对高斯烟团模型进行了改进,使其能够计算点源连续泄漏和风向变化的情况,应用场景更符合气态污染物泄漏事故的真实情况。随后模拟分析风速和大气稳定度对扩散的影响,并根据浓度分布对影响区域进行危险等级划分,以期为应急管理部门做出及时、准确响应提供技术支持。
1 大气扩散模型
高斯模型包括高斯烟羽模型和高斯烟团模型,高斯烟羽模型不包含时间参数,主要计算连续泄漏扩散在达到稳定时的污染物浓度分布;高斯烟团模型是瞬时扩散模型,用于计算瞬时泄漏产生的独立烟团随时间变化的扩散情况。主要研究气载放射性物质的实时扩散分布情况,故以高斯烟团模型为基础进行改进,使其满足计算点源连续泄漏以及风向变化的需求。
1.1 高斯烟团模型
点源瞬时泄漏产生的单个烟团的浓度分布计算公式为[15]

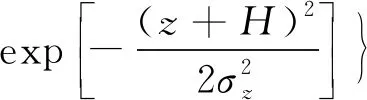
(1)
式(1)中:C(x,y,z,t)为t时刻空间点(x,y,z)上的浓度,kg/m3;Q为泄漏源瞬时泄漏的泄漏量,kg;u为环境风速,m/s;H为烟团的有效高度,m;σx、σy、σz分别为烟团在x、y、z方向上的扩散系数,其值与大气稳定度和烟团下风向距离x有关。
大气稳定度依据表1判断,各扩散系数具体计算公式如表2所示。
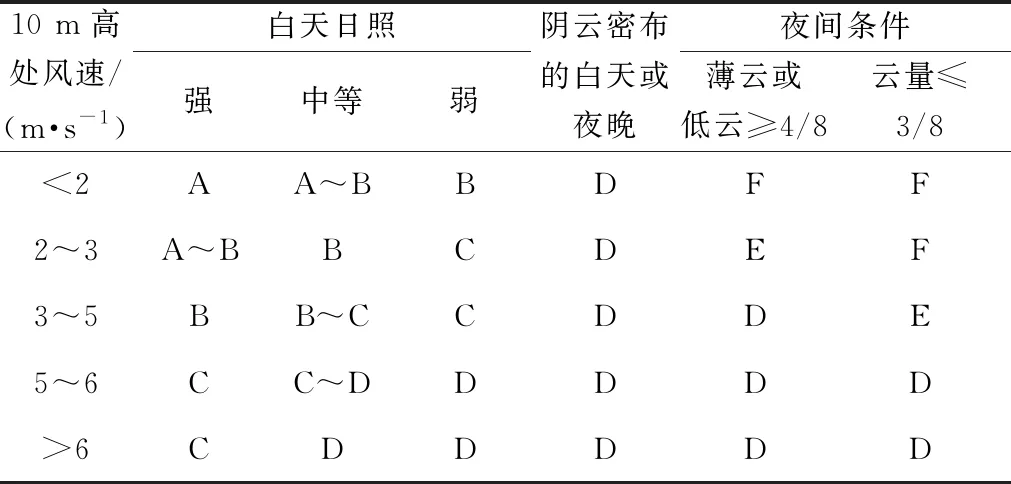
表1 大气稳定度等级

表2 扩散系数计算公式
1.2 连续泄漏条件下扩散计算
高斯烟团模型为瞬时泄露扩散模型,在计算连续泄漏扩散情况需要对模型进行改进。参考文献[12]的方法,将1个连续泄漏源在时间上进行划分,考虑为多个瞬时泄漏源。该连续源产生的污染物浓度分布即为多个瞬时源产生的污染物浓度分布的叠加。即:假设连续泄漏扩散时间为t,在时间t内以时间间隔Δt划分出n个瞬时泄漏源,每个瞬时泄漏源产生的烟云随风向扩散至t时刻的浓度分布由式(2)计算可得,这n个瞬时泄漏源所产生污染物的浓度叠加即为连续泄漏源所产生的污染物浓度分布,可表示为
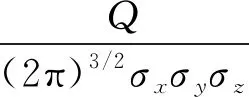
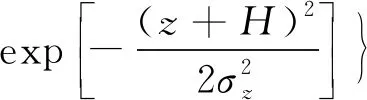
(2)
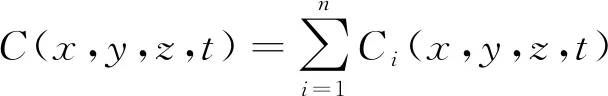
(3)
式(3)中:Ci为第i个瞬时泄漏源产生的烟云在t时刻的浓度分布,kg/m3。
1.3 变风向条件下扩散计算
标准高斯烟团模型中假设风向和风速为恒定参数,但在实际情况中风速和风向是随机变化的。参考文献[13-14]的方法,以泄漏源为原点,以泄漏初始时刻下风向为x轴正方向,垂直于风向方向为y轴,建立基准坐标系xoy。在风向发生变化时,以新风向建立瞬时坐标系x′oy′,两坐标系之间需要进行旋转与平移变换综合处理,坐标转换表达式为
y′=[y-ym(n)]cosβ(n)-
[x-xm(n)]sinβ(n)
(4)
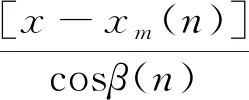
Z(n-1)
(5)
式(5)中:(x,y)为计算点在xoy坐标系中的坐标;(x′,y′)为计算点在x′oy′坐标系中的坐标;xm(n)、ym(n)分别为第n个烟云产生初始位置的横、纵坐标;β(n)为第n个时间单元的风向与基准坐标x轴之间的夹角。
2 程序设计及验证
2.1 程序设计
基于Python语言编写了大气污染物扩散模拟程序,包括污染源监测模块、气象监测模块和模拟计算模块。图1为程序的运行流程图,污染源监测模块对污染物的成分、释放速率等源项参数进行实时收集并传输至模拟计算模块;气象监测模块实时收集风速、风向、温度等气象参数并传输至模拟计算模块;模拟计算模块对源项数据、气象数据以及计算区域尺寸等用户自定义的参数进行处理,代入到数学模型中进行浓度分布计算,最终得到污染物在大气中的浓度分布云图或等值线图。
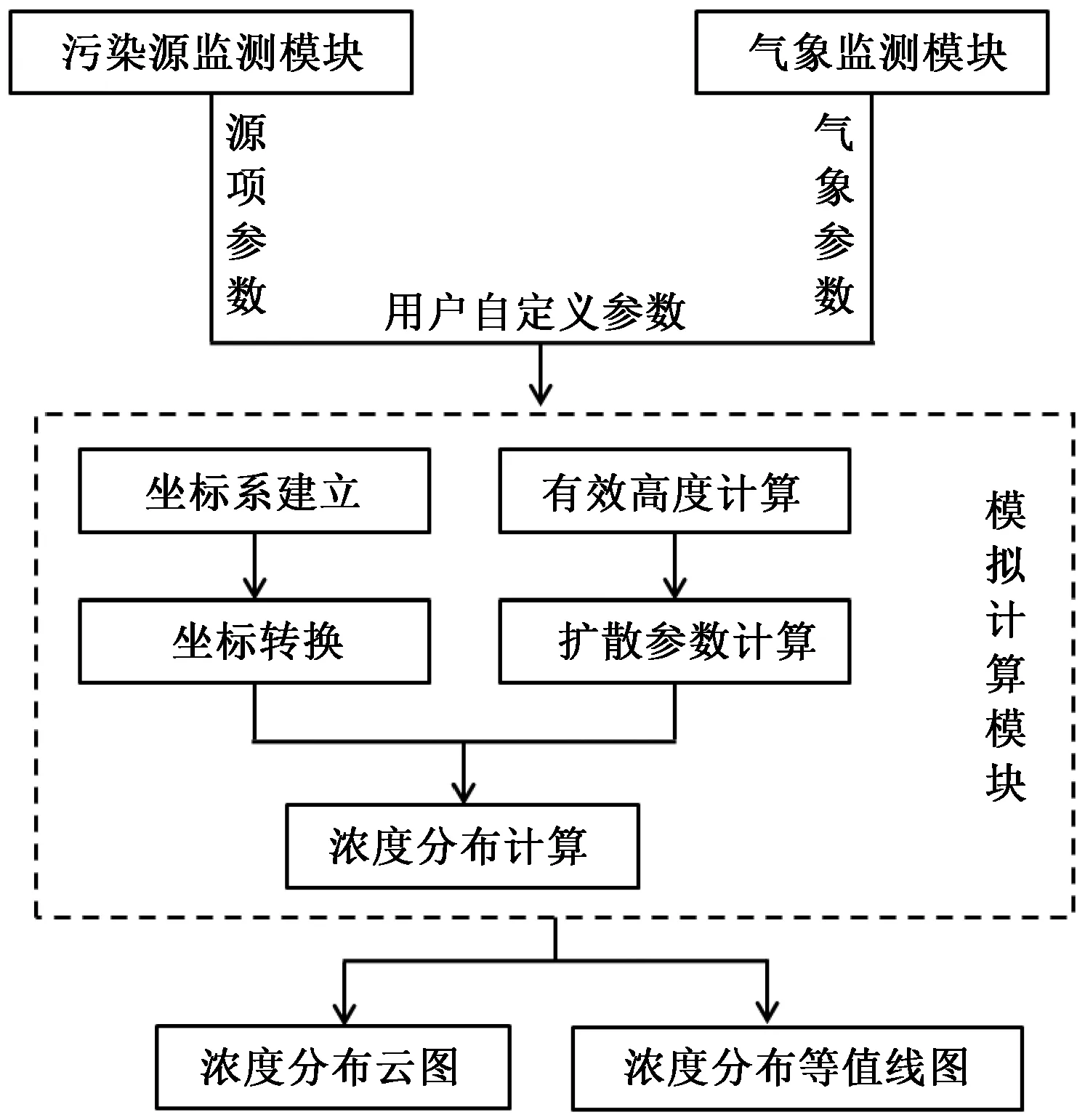
图1 程序流程图
2.2 模型验证
为验证所建立模型的可靠性,以美国开展的Burro系列液化天然气泄漏试验中9号试验为基准进行对比。Burro 9号试验参数为:泄漏速率18.4 m3/min,泄漏时间79 s,平均风速5.7 m/s,环境温度35.4 ℃,相对湿度12%[12, 16]。模拟值与试验值对比结果如图2、表3所示,模拟所得各体积分数分布情况与试验较为吻合,各体积分数的扩散距离与试验值误差在20%以内,可认为所建立模型具有一定的可靠性。而模拟结果与试验结果之间存在一定的误差可,原因可能为试验的风速和方向是随机变化的,而模拟设置的风速和风向为恒定值,风速和风向的变化导致出现误差。
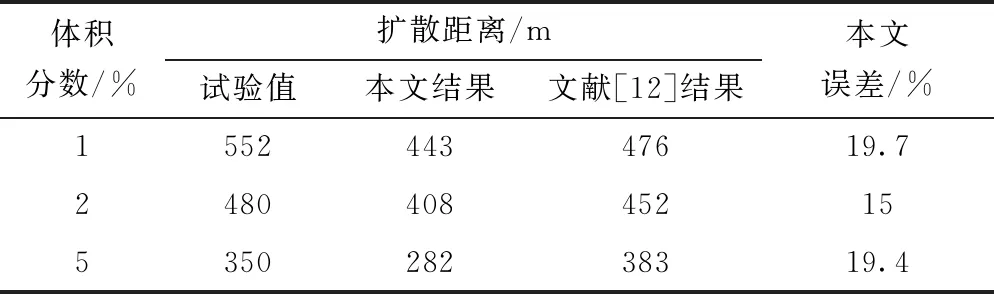
表3 试验结果与模拟结果对比
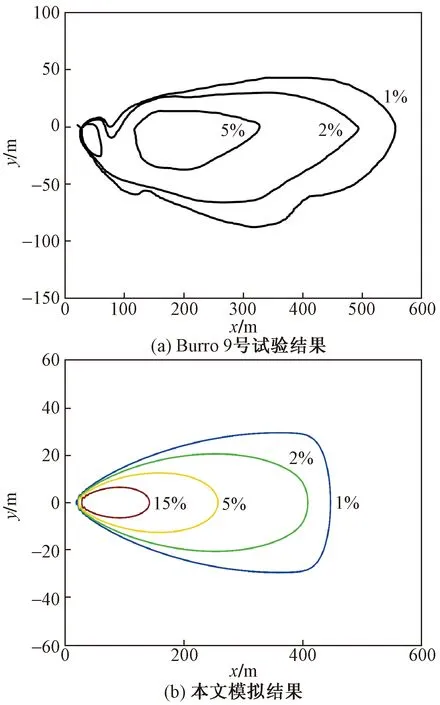
x、y分别为污染物在下风向、垂直风向上的扩散距离
3 污染物扩散模拟及分析
假设某工厂液化天然气储罐发生持续泄露,以泄漏初始时刻下风向为右手坐标系x轴正方向建立基准坐标系,以泄漏发生时为0时刻,各监测时刻的风速和风向如表4所示。泄漏点距地面高度10 m,参考文献[8]计算泄漏速率为8 kg/s,地面粗糙度1 m,大气稳定度为D,参考文献[12,17]按照气体质量浓度范围对扩散影响区域进行危险等级划分,区域划分及各区域边界取值如表5所示。

表4 模拟风况

表5 危险区域划分
图3给出了泄漏源所在高度平面的各级危险区域浓度分布。可以看出,随着泄漏时间的增加,扩散影响区域逐渐增长,在泄漏发生300 s时,轻度及以上危险区域面积达到22 679.89 m2。泄漏0~40 s时,风向为x轴正方向,扩散区域均匀发展。在泄漏40 s时,风向向y轴正方向偏转5°,扩散区域出现明显变形,扩散方向开始向跟随风向偏转。在泄漏320 s时,扩散区域已整体偏向变化后的下风向,趋于稳定。
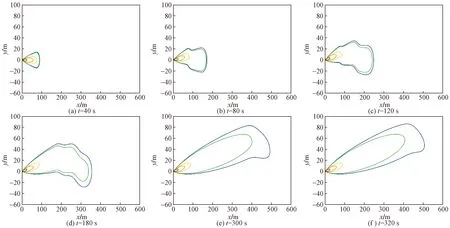
t为时间
3.1 风速对扩散的影响
风速对污染物在下风向的扩散起到主导作用,保持泄漏速率8 kg/s,地面粗糙度1 m,泄漏点距地面高度10 m,大气稳定度为D,风向及监测时刻与表3相同,在风速为2.45、4.4、6.7、9.35 m/s时(二级~五级风的平均风速),模拟污染物的扩散情况。
图4为泄露发生后,各级危险区域面积在不同风速下随时间变化的曲线。可以看出:4个等级危险区域的面积都随着扩散时间的增加先增大而后趋于稳定。风速对污染物扩散有较大影响,区域面积达到稳定所需时间随着风速的增加明显降低。出现上述情况的原因可能为:风对污染物有输送作用,风力越大输送能力越强,促使各区域面积快速达到稳定。但风速较大时污染物更为分散,不利于聚集形成高浓度区域,故各级危险区域面积随风速增加而降低。各风速下,中度危险区面积都高于其他区域,应重点防护。
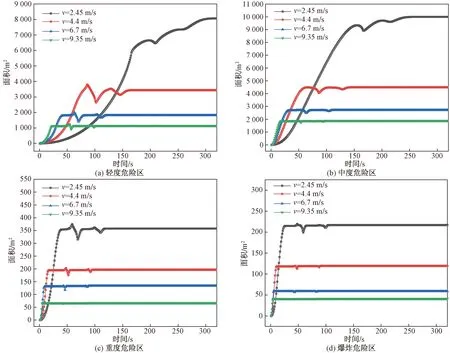
v为风速
3.2 大气稳定度对扩散的影响
由表2可知,大气稳定度对扩散系数有较大影响,而扩散系数影响着污染物的扩散范围。保持泄漏速率8 kg/s,地面粗糙度1 m,泄漏点距地面高度10 m,风速、风向及监测时刻与表3相同,在大气稳定度为A~E时,模拟污染物的扩散情况。
图5为泄漏发生后,各级危险区域面积在不同大气稳定度下随时间变化的曲线。可以看出:各大气稳定度下,危险区域面积都表现出随扩散时间增加先上升,而后趋于稳定的趋势。大气稳定度越好(A最差,F最好),各危险区域面积越大,达到稳定所需时间越久。原因可能为:大气稳定度越差,大气湍流强度越高,污染物更容易被稀释,难以聚集形成较高浓度的危险区域。各大气稳定度下,中度危险区面积都高于其他区域,应重点防护。
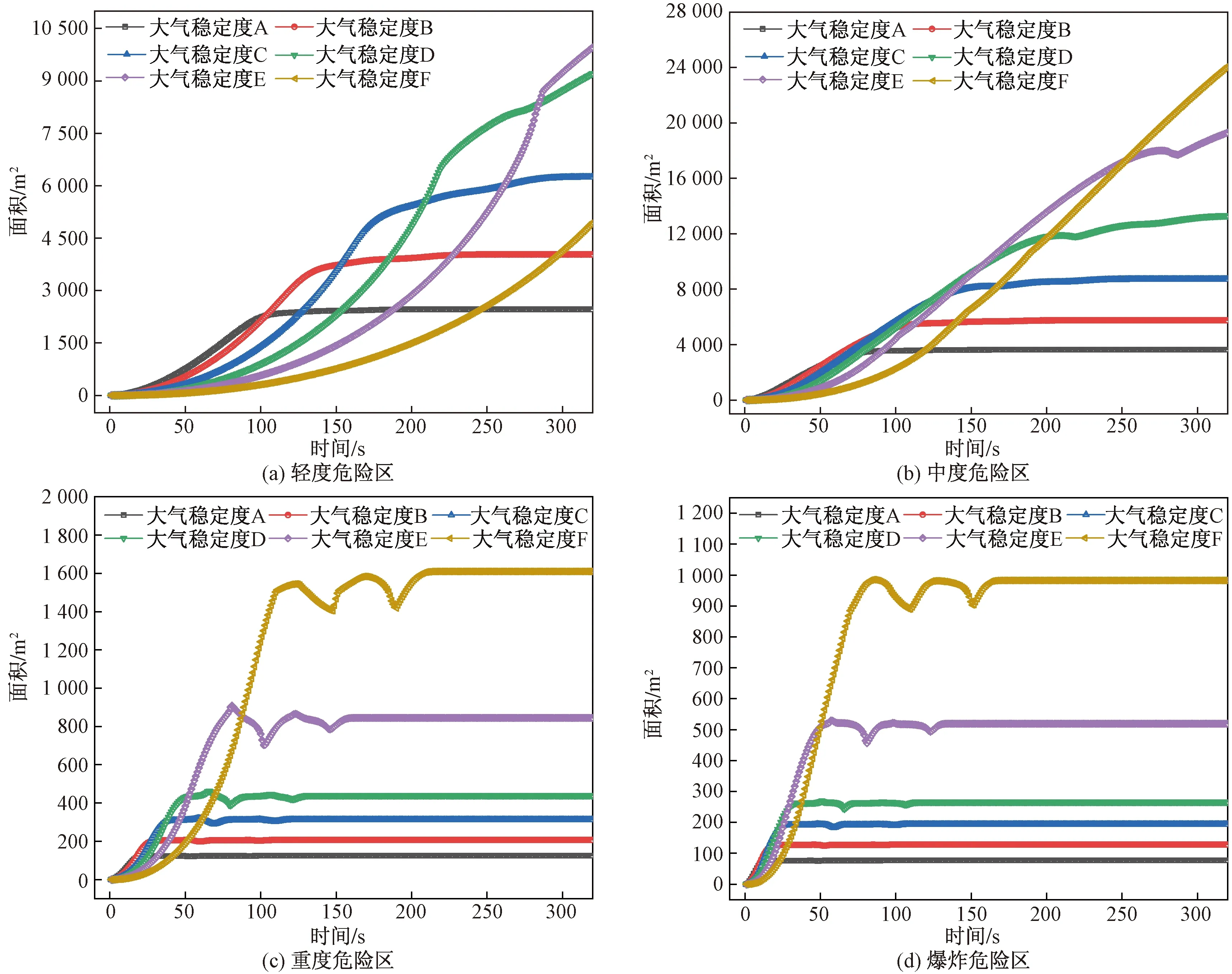
图5 大气稳定度对污染物扩散的影响
4 结论
基于高斯烟团模型,利用Python开发了变风向高斯烟团混合模型计算程序,可在风况变化和污染物连续泄漏扩散的场景下,模拟计算污染物浓度分布随时间变化的情况。基于此,模拟分析了风速和大气稳定度对污染物扩散的影响,得出如下结论。
(1)该模型通过时间分段处理和坐标转换的方法,实现了风况变化和连续泄漏扩散场景下,污染物扩散的浓度分布计算。经验证模型较为可靠,对突发事故造成的危险气体扩散范围和浓度分布预测具有一定帮助。
(2)各级危险区域的面积都随着扩散时间的增加先增大,而后趋于稳定。其中,达到稳定所需时间以及危险区域的面积都随着风速的增加而降低,随着大气稳定度的变差而降低。
(3)在各风速以及各大气稳定度情况下,中度危险区面积都高于其他区域,应重点防护。
