基于速度分配的航空器绿色滑行优化

孙若飞， 李杰， 万莉莉， 杨好天

(1.南京航空航天大学民航学院， 南京 211106； 2.南京航空航天大学通用航空与飞行学院， 南京 211106)

航空器在场面运行时排放大量的一氧化碳(carbon monoxide，CO)、碳氢化合物(hydrocarbon，HC)、氮氧化物(nitrogen oxides，NOx)等气体，污染机场环境，威胁人类健康。随着机场航班量的逐渐增多，航空对环境的负面影响越来越受到关注。在国际民航组织定义的标准起飞着陆循环中，滑行阶段的尾气排放最多[1]。

目前，对于场面滑行优化方面的研究，主要以滑行时间和油耗为优化目标。Chen等[2]着重考虑了速度的变化，并研究了油耗和CO、HC和NOx的排放；Zhang等[3]基于四维航迹提供滑行指导，建立了滑行优化模型，针对滑行时间、油耗和尾气排放进行优化；随后又提出了一种在线生成速度剖面的方法和具有时间窗和最大遍历时间约束的优化模型，旨在生成最优油耗的速度剖面，并实现对滑行优化更有效的处理[4]；Brown等[5]提出了一种基于自适应Mamdani模糊规则的系统来估计滑行时间及其不确定性；赵文涛等[6]则考虑了离场成本的最小化，提出基于推出率控制的滑行策略。

在确定优化目标的基础上，众多学者结合寻优算法和整数规划等方法进行求解。Weiszer等[7]提出了一种多目标进化算法优化框架，来解决跑道调度与机场场面运动相结合的复杂优化问题；Li等[8]考虑了滑行距离，转弯次数和滑行冲突建立了滑行优化模型，并使用遗传算法求解；何庶等[9]在传统的遗传算法基础上，设计了双链染色体，同时对滑行路径和优先级进行优化。

在滑行优化方面已经形成了较为全面和系统的优化方法，但仍有以下两个问题值得进一步研究：一是在优化过程中较少考虑尾气排放，关于尾气排放的定量研究很少；二是较少考虑滑行速度的改变对滑行时间、油耗和尾气排放的影响。针对上述问题，将速度分配和尾气排放考虑在内，构建滑行路径和速度的优化模型，结合遗传算法和Yen算法进行求解。

1 基于速度分配的航空器绿色滑行优化模型

1.1 速度优化模型

航空器到达或离开机场时，需要经管制员引导滑行至指定的停机位或跑道端，其滑行时间取决于滑行的速度与路径。航空器滑行过程中，为避免速度的任意变化而产生无数个决策变量，需要规定速度变化的剖面[10]。将滑行路径根据直线段和转弯段进行划分，将航空器在直线段上的运动规定为3个阶段：加速、匀速和减速，如图1所示。

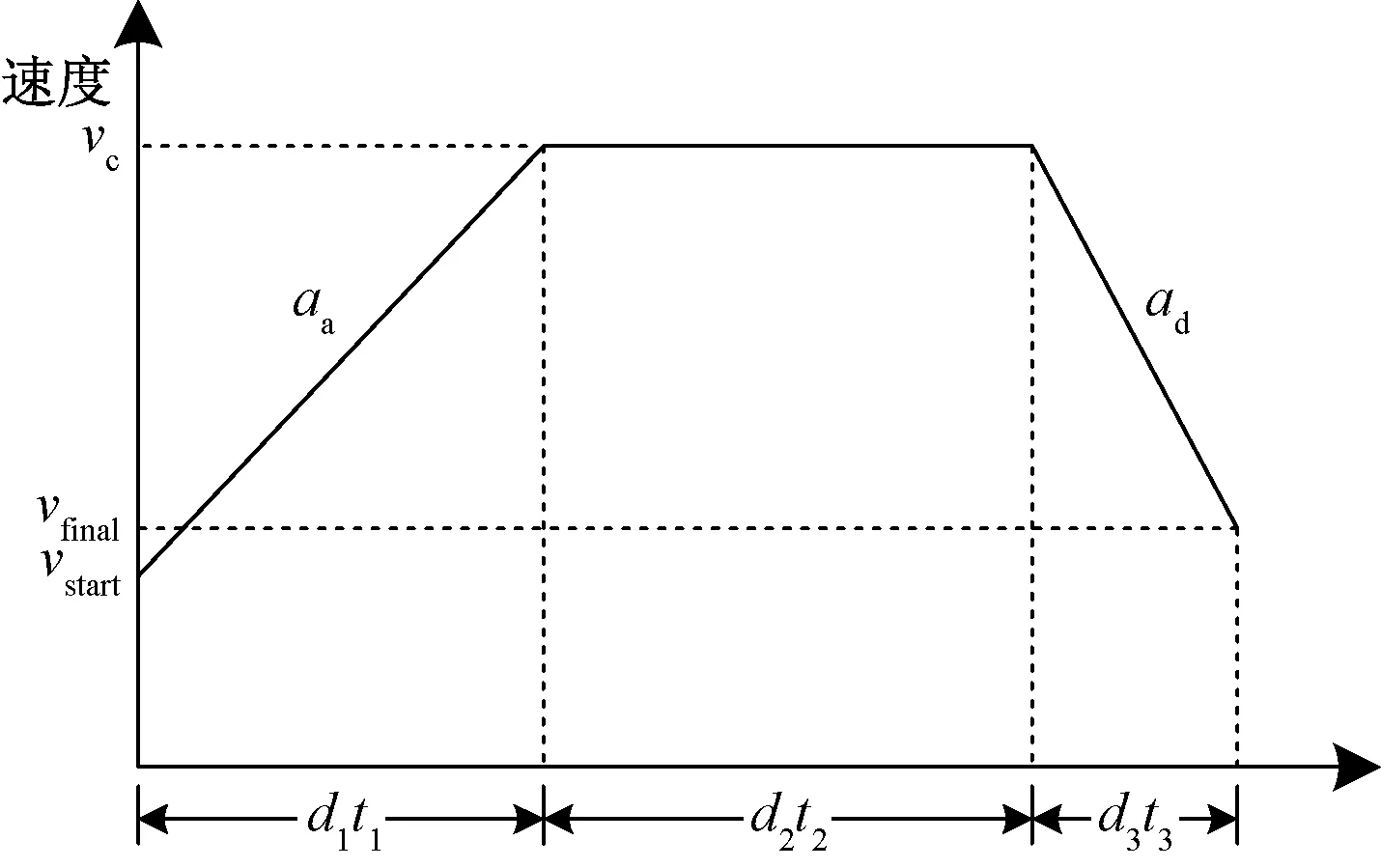
d1～d3、t1～t3分别为3个阶段的滑行距离和时间；vc、aa、ad分别为最大滑行速度、加速度和减速度；vfinal为最终速度；vstart为初始速度

由于直线与转弯段首尾相连，因此直线段的初始速度vstart等于0(从撤轮挡或等待后开始滑行)或转弯后的速度，最终速度vfinal等于转弯前的速度或0(停止等待或到达跑道外等待点)。

1.2 滑行时间和排放计算方法

1.2.1 滑行时间计算方法

航空器在指定滑行路径上的总滑行时间为直线段和转弯段滑行消耗的时间之和，可表示为

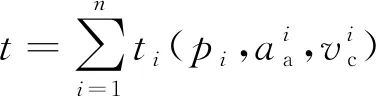
(1)

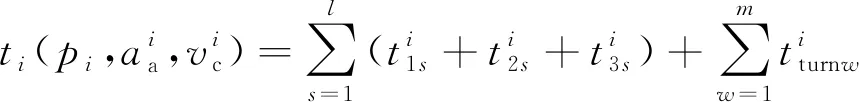
(2)

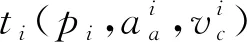
1.2.2 尾气排放计算方法

每小时油耗量定义为燃油流率ff，燃油流率与运行时间的乘积定义为油耗量F，消耗单位质量燃油排放的气体质量定义为排放指数EI，某种气体的排放量为排放指数与油耗量的乘积。选择CO、HC和NOx3种污染气体，其排放指数均在排放数据库公布。

燃油流率和排放指数需要通过发动机的推力系数(当前推力与最大推力的比值)计算得出。正常滑行和减速阶段取推力系数为7%，转弯阶段取推力系数8%，加速阶段通常取推力系数为7%～30%[11]。根据加速度与推力的关系，计算每时每刻的推力，通过插值法计算燃油流率和排放指数。

分析快速存取记录器(quick access recorder，QAR)数据发现，发动机推力只有在加速度较大时才会发生明显变化，在减速阶段推力变化不大[12]。因为驾驶员通常会为节省时间而加油门以增加发动机推力。但在减速时以踩刹车的方式来替代收油门，以避免发动机功率的增减带来的时间消耗。

总油耗为直线与转弯段的油耗之和，可表示为

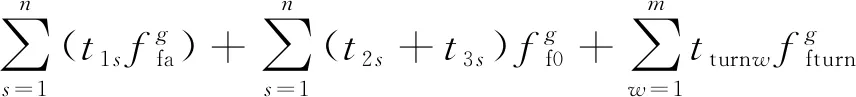
(3)

尾气排放量为油耗与排放指数的乘积，可表示为

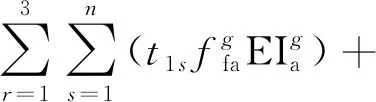
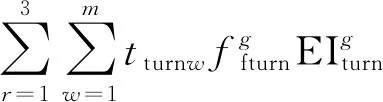
(4)

推力的变化会导致速度变化，图2为航空器的受力分析图。

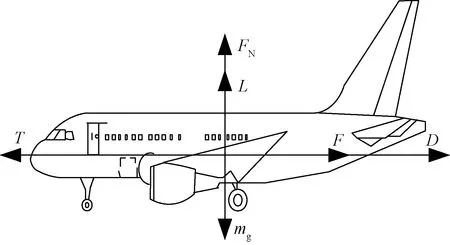
mg为重力；F为滚动摩擦力；T为推力；D为气动阻力；L为升力；FN为支持力

地面运行时将升力忽略不计，推力可表示为

T=ma+Cmg

(5)

式(5)中：m为航空器质量，本文以各机型最大起飞重量近似替代；a为滑行的加速度；g为重力加速度，取9.81 m/s2；C为滚动阻力系数，取0.015。

1.3 滑行成本计算方法

引入滑行成本权衡时间和排放两个目标。滑行成本包括时间和环境成本。时间成本是航班花费时间产生的，是滑行时间与时间成本系数的乘积；环境成本是CO、HC和NOx3种污染尾气的排放成本，为排放量与排放成本系数的乘积。滑行总成本为时间成本与尾气排放成本之和。表1和表2分别为时间和排放成本系数[13]。

表1 时间成本系数

表2 CO、HC和NOx排放成本系数

2 航空器滑行策略优化方法

在不影响模型适用性的前提下，本文的问题进行如下假设：①航空器在滑行道上的运行不受起飞和着陆的影响；②在进行仿真实验时所有航空器对应的跑道和机位信息均已知；③在仿真过程中未出现因特殊原因滑行道不可用的情况；④假定航班以最大起飞重量起飞。

2.1 目标函数

以最小化滑行时间、尾气排放和滑行成本为优化目标，其表达式分别为

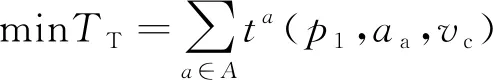
(6)

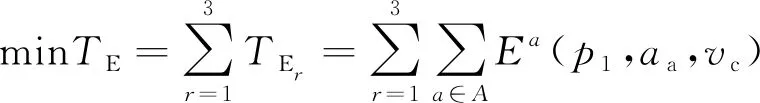
(7)

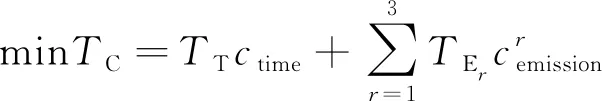
(8)

式中：TT、TE和TC分别为所有航空器的总滑行时间、尾气排放和滑行成本；r=1、2、3分别表示污染物类型为CO、HC和NOx。

2.2 约束条件

考虑到实际运行情况，需要为航空器设置一些约束条件。

(1)为保证舒适度和安全性，最大滑行速度和加速度的取值要满足合适的区间，减速度ad取 0.5 m/s2。

0≤vc≤13.88 m/s

(9)

0≤aa≤0.98 m/s2

(10)

(2)离场航空器的开始滑行时刻应不早于预计推出时刻，并在不晚于预计离场时刻到达跑道外等待点；对于进场航空器，令其在预计着陆时刻开始滑行，因进场航空器优先级较高，故不对其结束滑行的时刻进行约束。

(11)

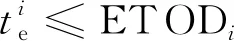
(12)

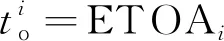
(13)

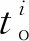
(3)滑行中的前后机之间应满足一定的安全距离。

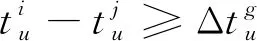
(14)

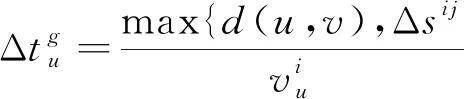
(15)

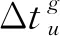
(4)滑行冲突解脱约束。

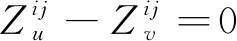
(16)

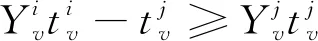
(17)

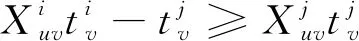
(18)

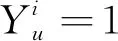
表示航空器i从节点u滑行到节点v，否则

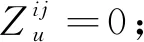
2.3 算法设计

2.3.1 Yen算法

利用Yen算法为航空器生成多条最短路径，计算步骤主要分为两部分：①利用Dijkstra算法计算1条最短路径P(1)；②在P(1)的基础上依次计算其他的k-1条最短路径。除终点外，定义其他节点为偏离节点，计算每个偏离节点到终点的最短路径，再与之前起点到偏离节点拼接起来，进而求得最短偏离路径。

2.3.2 NSGA-Ⅱ算法

NSGA-Ⅱ是遗传算法的一种，用于解决多目标优化问题。通过模拟自然选择过程搜索最优解，具有较好的收敛性能。传统遗传算法的参数固定，容易使算法收敛至局部最优解，为了使其能够有效地进行全局搜索，通过多次运行分析参数的可靠性，运行内存4.00 GB，CPU为i7- 6500U 2.5 GHz。

(1)迭代次数：假定变异概率、交叉概率、种群数量分别为0.1、0.9、500。比较迭代次数为10、50、100、200、300、400和500时的适应度值和运行时间，结果如图3和图4所示，迭代次数为200次时收敛性能较好且CPU时间较短。

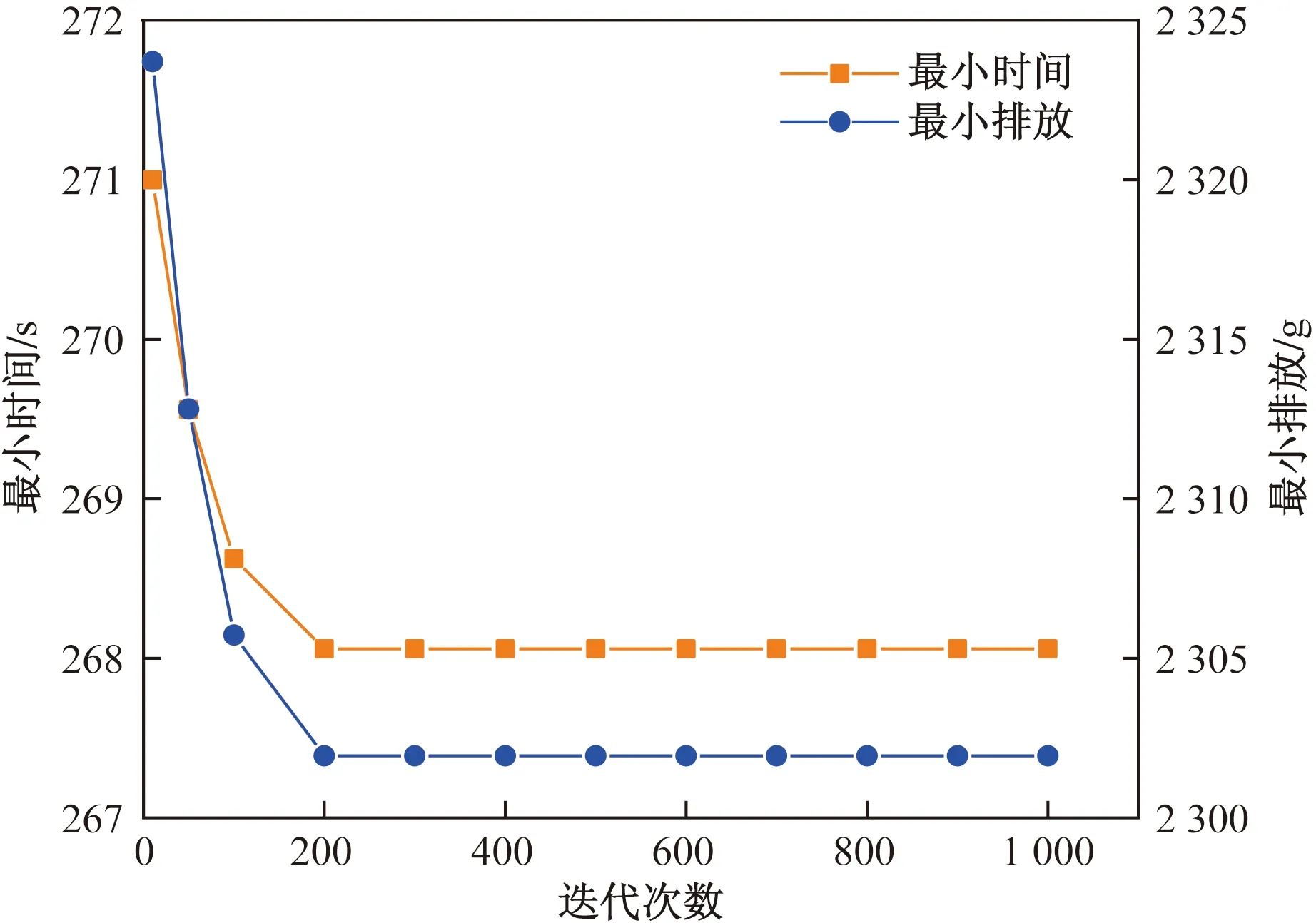
图3 不同迭代次数下的最小时间和排放

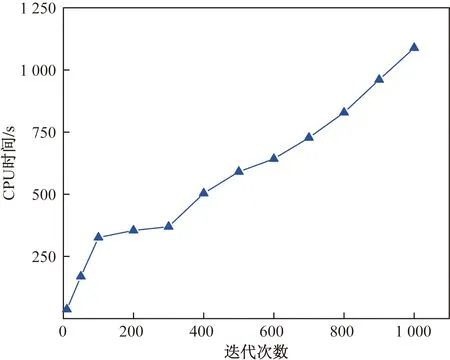
图4 不同迭代次数下的CPU时间

(2)种群数量：假定变异概率、交叉概率、迭代次数分别为0.1、0.9、200。比较种群大小为10、50、100、200、300、400和500时的两个目标函数和算法运行时间，结果如图5、图6所示，种群数量为200时，收敛性能较好且CPU时间较短。

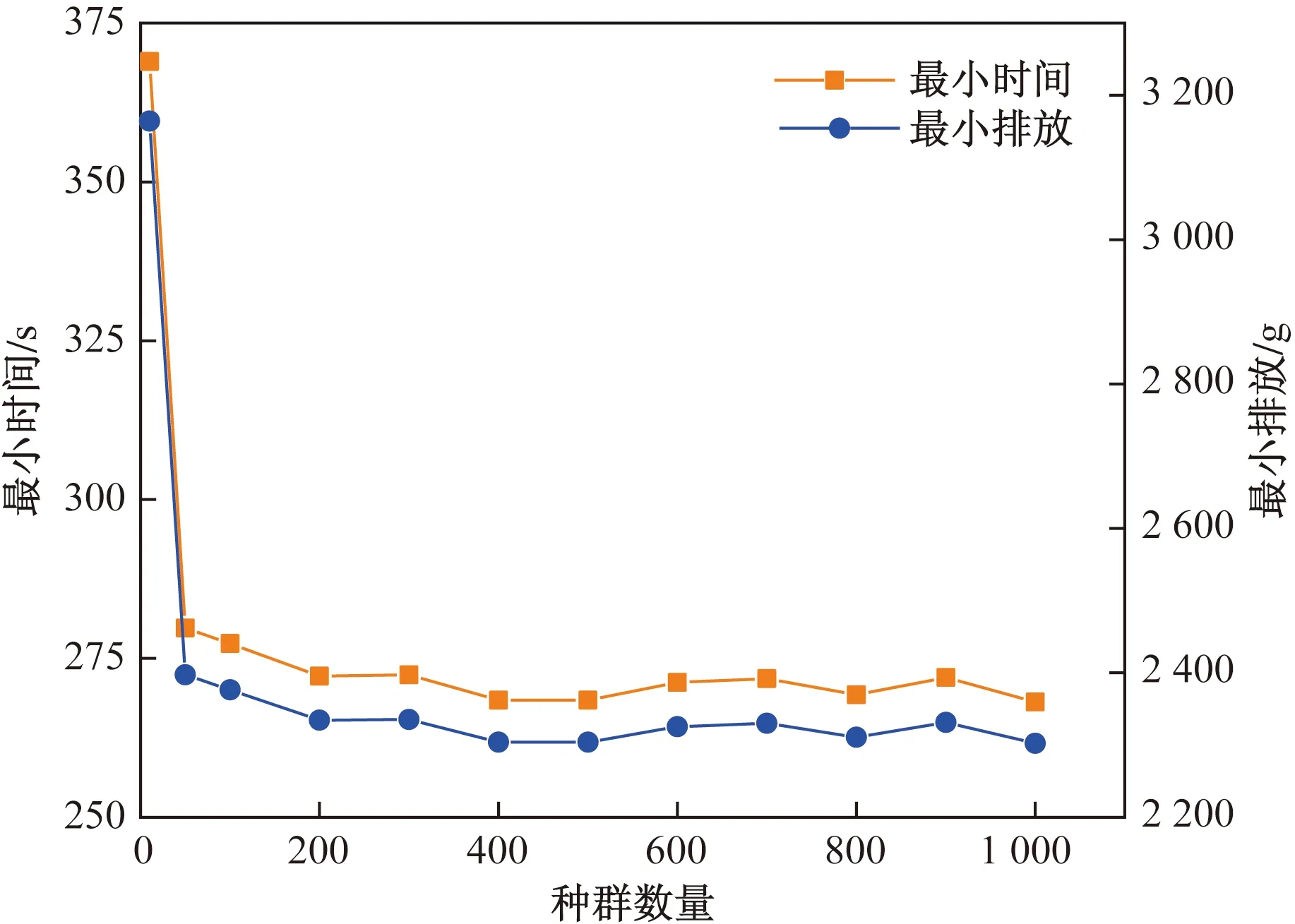
图5 不同种群数量下的最小时间和排放

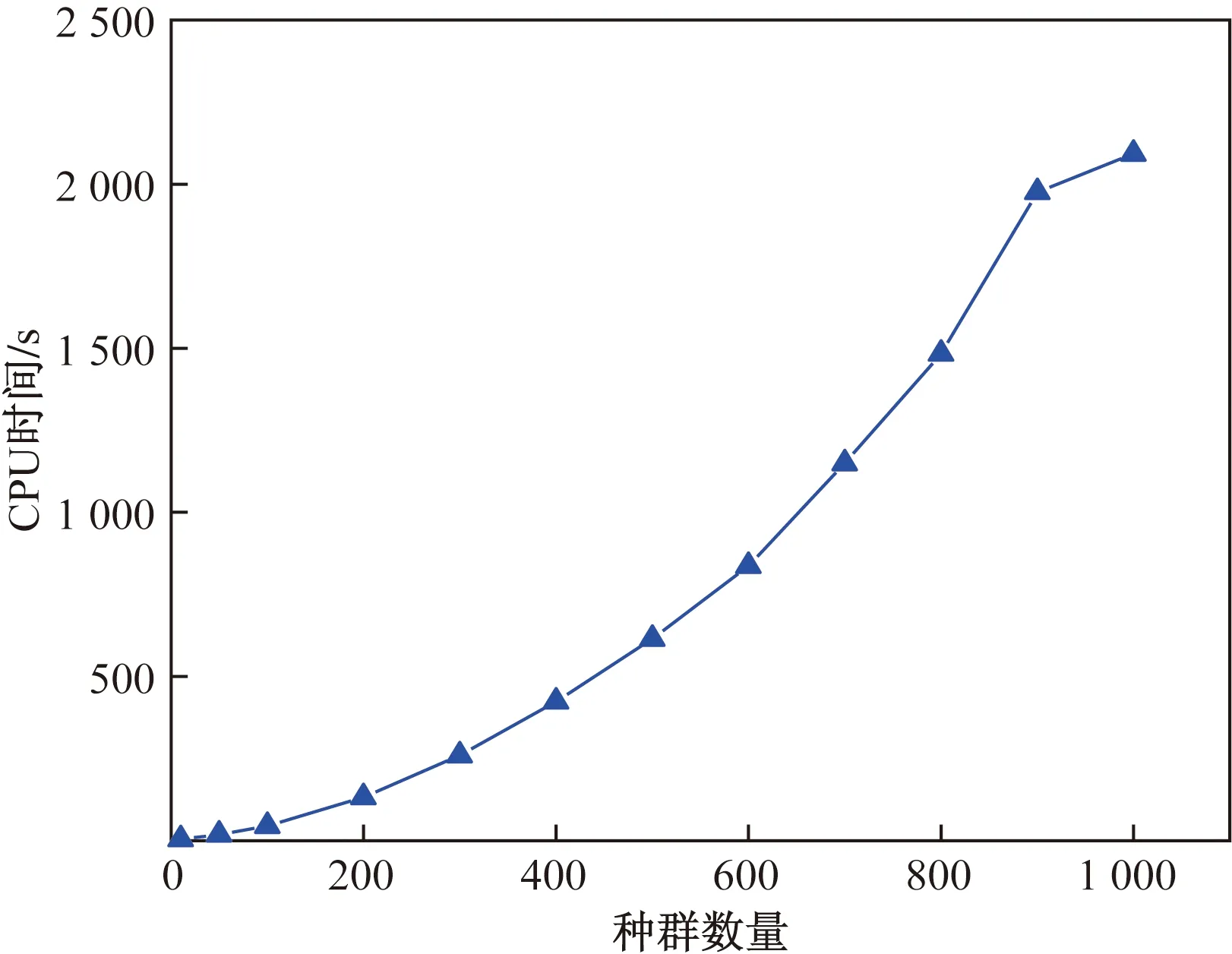
图6 不同种群数量下的CPU时间

(3)交叉/变异概率：由于遗传算法的交叉和变异概率具有较强的关联性，因此设定交叉概率分别为0.5、0.55、0.6、0.65、0.7、0.75、0.8、0.85、0.9、0.95、1.00，变异概率分别为0、0.05、0.1、0.15、0.2、0.25、0.3、0.35、0.4、0.45、0.5。对两者的所有组合进行运行验证，结果表明，交叉概率为0.85，变异概率为0.05时，收敛性能较好且CPU时间较短。

2.3.3 基于速度分配的滑行优化方法

所采用的基于速度分配的滑行优化框架由Ravizza等[14]首次提出，该算法将最短路径问题同滑行速度优化结合起来，并整合到同一个程序框架中。在优化目标和适用场景等方面进行了改进，算法流程如下。

步骤1根据航班的撤轮挡时刻和落地时刻对航班排序。

步骤2使用Yen算法为每一架航班选择滑行时间最优或较优的3条路径。

步骤3将所有航空器的3条滑行路径利用NSGA-II算法进行速度优化，得到时间和排放的3组Pareto解。

步骤4在每架航班的3组Pareto解中，保留所有的非支配解生成近似Pareto前沿，并将保留的非支配解离散为等距的5个点。

步骤5在没有冲突的前提下，将所有的航班的近似Pareto前沿累加，形成近似的全局Pareto前沿，通过计算滑行成本来选择最优的滑行策略。

3 算例分析

3.1 数据准备

3.1.1 浦东机场网络模型

选择上海浦东国际机场进行仿真实验，依据发布的机场图绘制浦东机场网络模型如图7所示，标注重要节点如停机位、强制等待点、转弯点以及冲突热点区域，测量所有连通的节点对之间的距离生成邻接矩阵表。

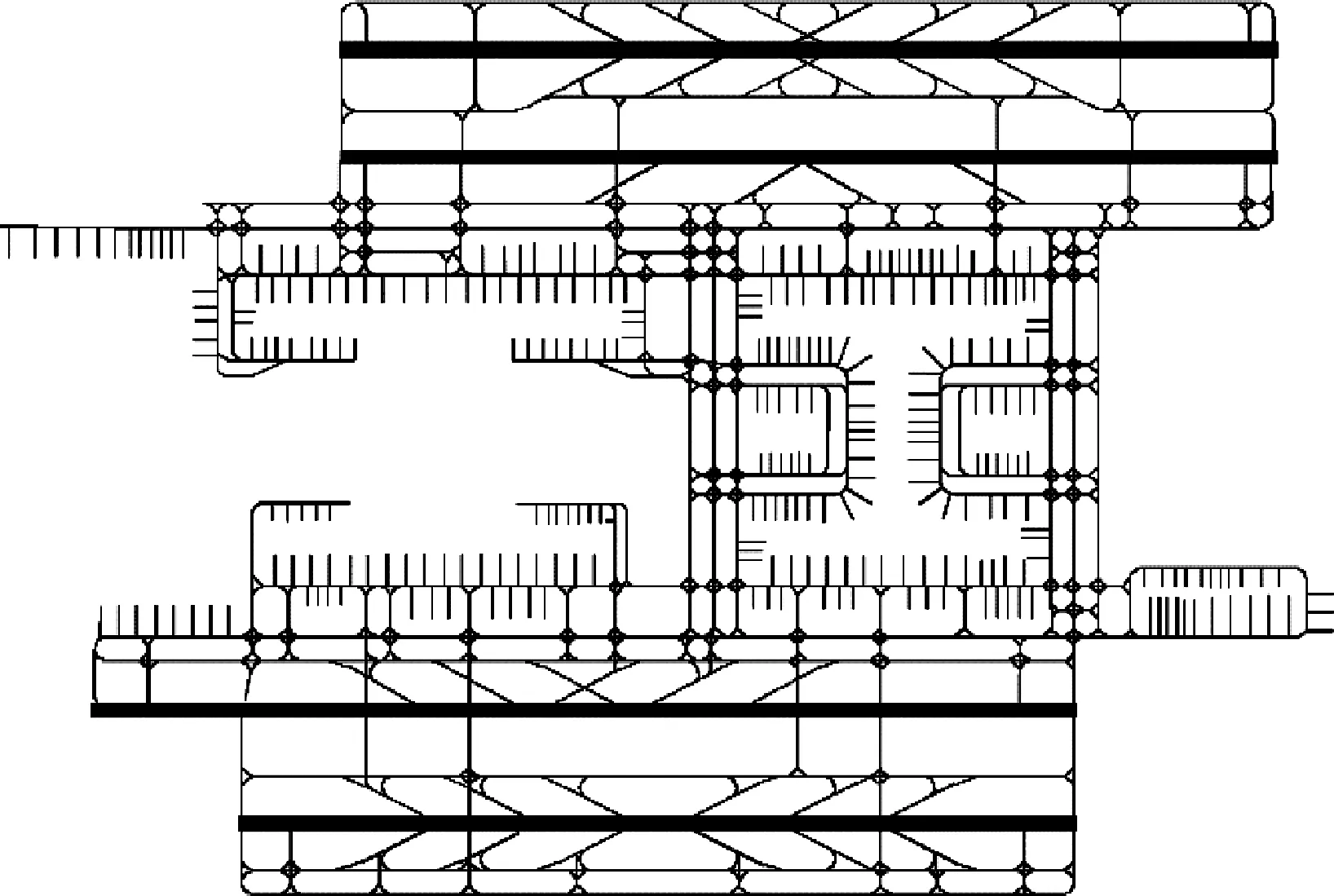
图7 浦东机场网络图

3.1.2 航班和机型数据

选择2019年3月浦东机场16架航班仿真运行，机型信息如表3所示，其中燃油流率和排放指数给出推力系数为7%和30%下的数值。相关机位和主要滑行道已经标注在网络图上。观察航班数据发现，航班大都选择最近的跑道或机位，且所选时段内东飞行区的航班运行相对复杂，所以选择东运行区中的航班进行仿真优化。图中标注了公布的各种等待点，航班在到达等待点之前，需根据场面滑行情况决定是否在此等待，在经过强制等待点时需要停车等待。

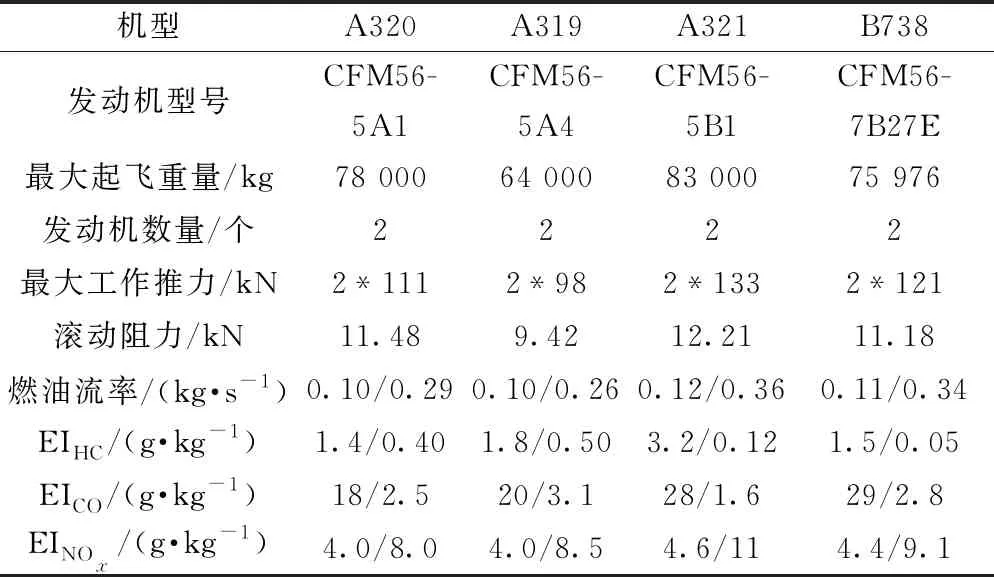
表3 相关机型及发动机参数

3.2 优化结果

通过仿真计算为该时段所有航班生成的近似全局Pareto前沿如图8所示。

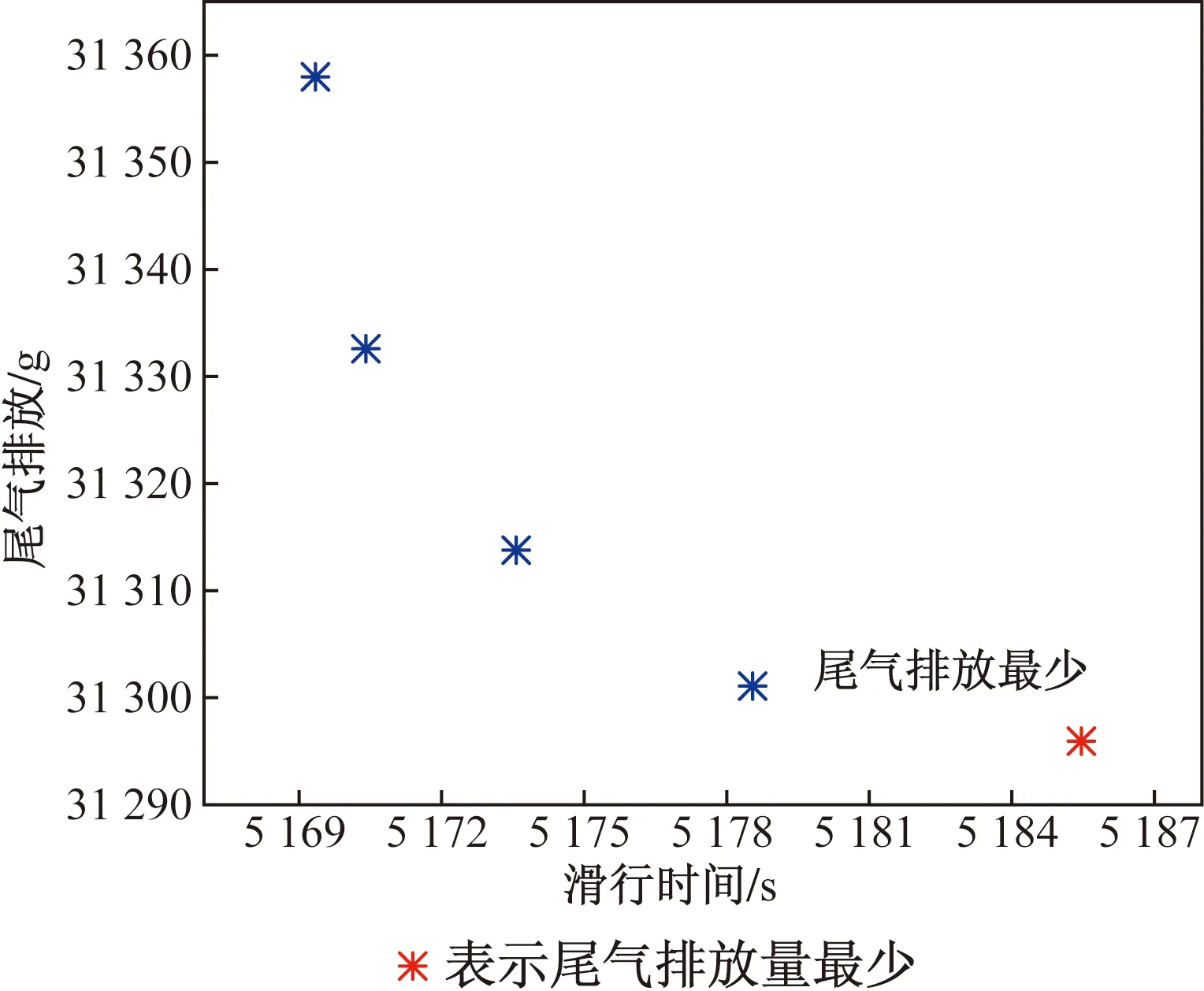
图8 全局Pareto前沿

在此基础上计算滑行成本，选取图9中的最低点即滑行成本最小的点作为最优的滑行策略。图9的全局Pareto前沿中，得到了滑行成本最小的策略后，选择该策略对应的所有航班的滑行速度和滑行路径。

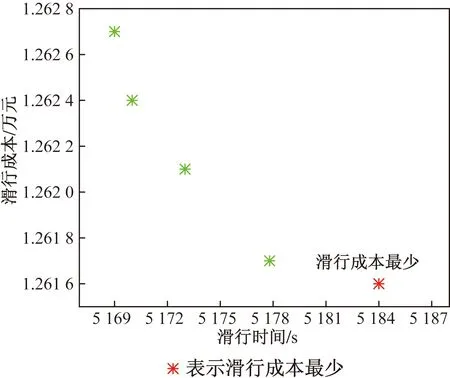
图9 成本与时间的Pareto前沿

将仿真运行和计算得到的滑行策略方案，与未进行优化的方案比较，以验证滑行调度策略的可行性。优化前的对照组设置为：直线段以8 m/s匀速滑行，推力系数设置为7%；转弯段以5 m/s匀速滑行，推力系数设置为8%。如表4所示。

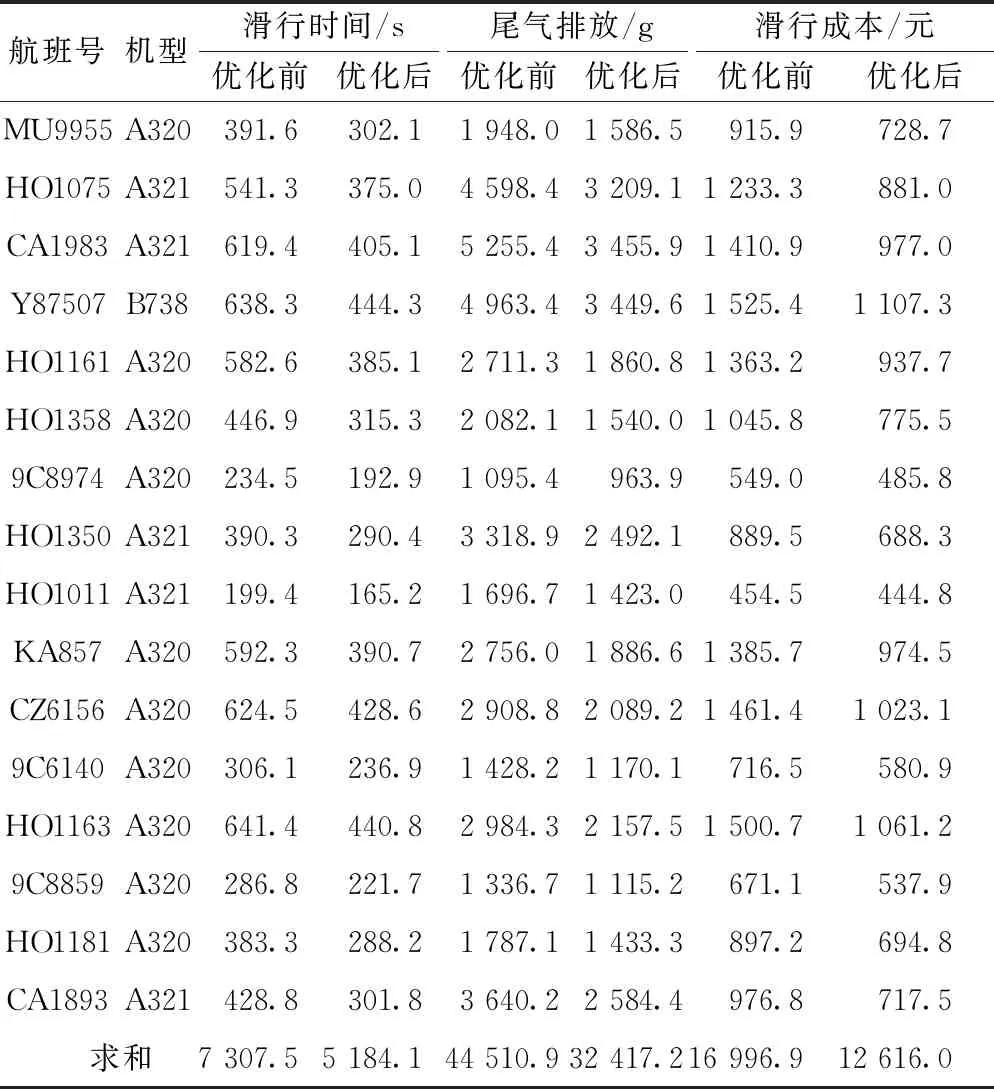
表4 优化前后结果对比

对比计算可知，在优化后的滑行调度策略下，滑行时间较优化前降低了21.82%，尾气排放降低了27.17%，成本降低了25.77%，且没有发生滑行冲突，证明该优化策略能有效地降低滑行时间、尾气排放和滑行成本。其中A320机型3个目标分别降低29%、25%、26%；A321机型分别降低了29%、29%、25%；B738机型分别降低了30%、30%、27%；

且在整个滑行过程中没有发生滑行冲突，证明该优化策略能有效地降低滑行时间、尾气排放和滑行成本。

4 结论

(1)针对滑行中的航空器，对其路径和速度进行优化。离散化速度剖面，建立滑行时间、尾气排放和滑行成本最小的目标函数，以浦东机场航班为实例，结合遗传算法和Yen算法进行仿真，得到最优的滑行路径和速度剖面。

(2)本文模型和优化算法可在保证无滑行冲突的前提下，为航班分配优化的路径和速度剖面，与优化前相比，时间、尾气排放和成本分别降低了21.82%、27.17%和25.77%。

随着“碳达峰”“碳中和”等概念的提出，未来可将优化的重点放在航空运行的碳排放上。同时，以后的研究中可以寻找实际运行的滑行时间、油耗、尾气排放排放和成本系数数据，提高数据对比的准确性，并在此基础上加入其他影响滑行的因素，与停机位分配、推出率控制和进离场排序等优化策略结合，实现场面运行的整体优化。