高频变压器漏感参数对绕组形变的全局灵敏度分析

2022-07-11陈健万妮娜郭昊徐溧付焱燚陈彬

科学技术与工程 2022年16期

陈健，万妮娜，郭昊，徐溧，付焱燚，陈彬*

(1.三峡大学电气与新能源学院，宜昌 443002； 2.国网湖北省电力公司宜昌供电公司，宜昌 443000；3.智能带电作业技术及装备(机器人)湖南省重点实验室，长沙 410100； 4.带电巡检与智能作业技术国网公司实验室，长沙 410100； 5.国网湖南省电力有限公司技术技能培训中心，长沙 410100)

基于大功率高频变压器的磁耦合DC/DC变换器是实现大规模直流源互联、兆瓦级直流电压变换的核心设备[1-3]。由于其工作电流较大，当高频变压器发生短路故障时绕组电流激增，致使高频变压器绕组受力变形。此外，随着绕组结构发生改变，其空间磁场强度分布也会随之改变，从而导致高频变压器漏感参数发生改变。漏感参数过大将会降低变换器的输出效率，漏感参数过小则不能实现零电压开关[4-5]。因此，研究绕组形变对漏感参数的影响，分析其对不同形变种类的灵敏度，对高频变压器的可靠稳定运行具有重要意义。

在计算高频变压器漏感参数的方法中，有限元仿真可以充分地考虑复杂的绕组结构，对于分析复杂的绕组形变具有很高的精度[6-8]。然而有限元仿真计算效率低且不能给出漏感参数与绕组结构的具体函数形式，难以对其进行全局灵敏度分析。响应面法将数理统计与试验设计相结合，拟合出设计变量与响应变量之间的函数关系式，是进行灵敏度分析的有效方法，已广泛应用于各个领域[9-10]。漏感参数对于绕组形变的灵敏度分析包括了局部灵敏度分析和全局灵敏度分析。局部灵敏度主要体现了单个变量对漏感参数的影响，不能体现出各变量之间的交互作用。在全局灵敏度分析中，Sobol’灵敏度分析方法是一种基于方差的蒙特卡罗法，其形式简单、计算简便，已广泛应用于生物、物理、化学等各个领域之中[11-12]。文献[13]通过对比Sobol’灵敏度分析方法和其它灵敏度分析方法，认为Sobol’法是最有效的灵敏度分析方法之一，其不仅可以考察单个变量对函数的影响，还考虑了各变量之间的相互作用。文献[14]采用Sobol’灵敏度分析方法分析了高、低压绕组对地自电容、互电容以及高低压绕组自感、互感对绕组变形的灵敏度，揭示了各电气参数与绕组变形种类的内在联系。

针对高频变压器漏感参数对绕组形变的全局灵敏度分析问题，以一台额定容量为200 kVA，额定工作频率为10 kHz的高频变压器为研究对象，首先通过响应面法、中心复合试验设计以及有限元仿真构建了漏感参数的二阶和三阶响应面模型。其次，基于Sobol’灵敏度分析方法和蒙特卡罗抽样方法，对高频变压漏感参数进行灵敏度分析，揭示出不同形变种类对漏感参数的影响关系，为高频变压器的结构设计以及绕组形变检测提供了指导。

1 响应面模型及试验设计方法

1.1 响应面模型基本理论

响应面法(response surface methodology, RSM)是一种有效的参数灵敏度分析方法，该方法将数理统计与试验设计相结合，拟合出设计变量(因素)与响应变量(目标值)之间的函数关系式。响应面模型的阶数越高，其精度就越高，但表达式则越复杂。基于选定的响应面模型，对指定的设计参数进行试验设计采样并获取样本值，最后通过最小二乘法确定待定系数，最终得到实际模型的显式函数。响应面模型可以代替真实模型进行参数灵敏度分析。

二阶和三阶响应面模型的表达式分别为[14]

(1)

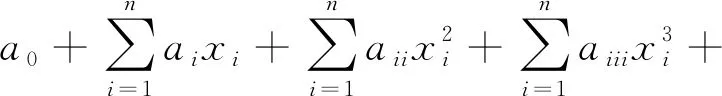
(2)

式中：y(x)为响应变量；xi、xj、xk为设计变量；n为设计变量的数量；a0、ai、aji、aij、aiii、aiij、aijk为待定系数，其个数N与响应面模型阶数和设计变量个数n有关。

以三阶响应面模型为例，其个数为

(3)

对指定的设计参数进行M次试验设计采样，得到样本值为y′=(y′(1),y′(2),…,y′(M))T，则响应面模型可用矩阵表示为

y′=Φα+ε

(4)

式(4)中：α为待定系数矩阵；ε为误差矩阵；Φ为样本点设计参数数据矩阵，可表示为[15]

(5)

通常采用最小二乘法来估计回归系数的值，因此待定系数α可以通过最小二乘法拟合得到，即

α=(ΦTΦ)-1(ΦTy′)

(6)

1.2 CCD试验设计

采样点的选取直接决定了响应面模型的拟合精度，因此需要通过试验设计生成合理的采样点。响应面分析的试验设计方法中，中心复合设计(central composite design, CCD)和Box-Behnken设计(Box-Behnken design, BBD)是最为经典的试验设计方法，此外还可以采用二次饱和设计、均匀设计、田口设计等方法。目前，CCD是运用最为广泛的试验设计方法，原因在于：①通过恰当地选择轴点坐标，可以使CCD为可旋转设计，从而可以在各个方向上提供同等精度的估计；②通过恰当地选择CCD试验设计的中心试验次数，可以使CCD是正交的或者是一致精度的设计，进而确定最优点位置[16]。因此，选择CCD试验设计方法确定绕组形变变量对漏感参数影响的试验方案。

CCD试验设计的二维和三维分布如图1所示，其中，1为设计变量的上水平，-1为设计变量的下水平。此外，由于轴向点a值的存在，使CCD获得最优解过程的搜索范围较BBD获得的搜索范围更广[17]。

Z1、Z2、Z3为三维坐标轴的坐标名称

1.3 响应面模型误差分析

由于通过试验设计确定的样本点的分布具有随机性，且少量样本不能完全代表全局变量。为了验证响应面模型是否具有足够的精确性和鲁棒性，借助式(7)计算拟合优度指标R2，对响应面模型进行精度分析。拟合优度指标系数越接近于1，则响应面模型的精度越高、拟合误差越小。

(7)

(8)

(9)

基于上述分析，响应面建模流程如图2所示，其中要求拟合优度指标大于0.99，拟合最大相对误差不大于1%。

图2 响应面模型建立流程

2 高频变压器模型及响应面模型的建立

2.1 高频变压器模型几何参数

所研究的高频变压器额定容量为200 kVA，额定工作频率为10 kHz，原、副边绕组额定电压为1 kV。高频变压器结构示意图如图3所示，样机实物如图4所示，具体参数如表1所示。原边绕组和副边绕组的层数均为1层，每层绕组包含有7匝方形利兹线。利兹线的尺寸为11.35 mm×11.35 mm，股数为2 128股，单股直径为0.2 mm，绞合方式为同心绞。

表1 高频变压器模型主要参数

r1为副边绕组内半径为；r2为原边绕组内半径；v1为副边绕组匝间距离；v2为原边绕组匝间距离

2 128为所使用的变压器绕组每匝利兹线导体的总股数，采用的利兹线为方形利兹线，19和112表示方形利兹线共包含19个子束、每个子束由112股绝缘细导线组成

采用ANSYS/Maxwell电磁场分析软件建立了高频变压器二维仿真模型。高频变压器绕组导体为利兹线，其单股直径小、股数多、绞合结构复杂。

为了降低建模难度、减少仿真时间同时保证计算精度，引入填充系数将利兹线等效为等面积的方形导体，等效后方形导体电导率seff=1.85×107S/m[18]。

由于变压器铁心窗口内外漏磁场的分布存在一些差异，为了更加精确地计算变压器铁心内外漏磁能量。将图3所示的变压器模型总的漏磁能量划分为铁心内部和铁心外部。图5给出了未发生绕组形变时，高频变压器的磁场强度和电流密度分布。

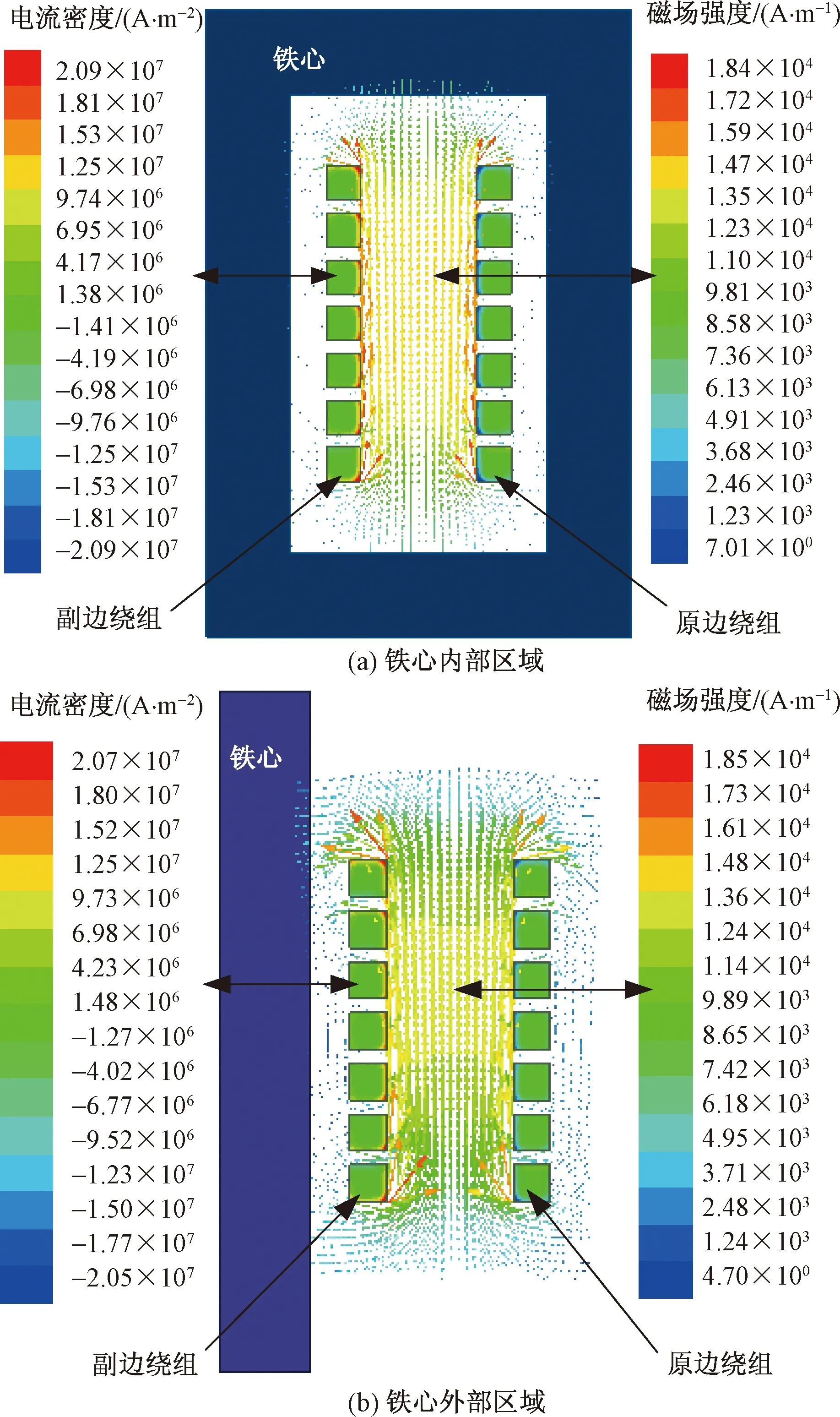
图5 磁场强度和电流密度分布

根据上述仿真计算获取的单位长度的漏磁能量，高频变压器的漏感参数的计算公式为

Lσ=2(WinMLTin+WoutMLTout)/I2

(10)

式(10)中：Lσ为漏感参数；Win、Wout分别为铁心内部区域和外部区域的单位长度的漏磁能量；MLTin、MLTout分别为铁心内部区域和外部区域的平均匝长；I为电流有效值。

当高频变压器绕组发生形变后，空间中的磁场强度分布将发生改变，高频变压器漏感参数也会随之改变，因此将建立高频变压器漏感参数的响应面模型。在高频变压器发生短路故障时，绕组会受到较大的径向和轴向电磁力作用，径向力使副边绕组内径缩短、原边绕组内径增加，轴向力使两绕组高度缩短[19]。因此，选取副边绕组内半径r1、原边绕组内半径r2、副边绕组匝间距离v1、原边绕组匝间距离v2作为响应面模型的输入变量。为了便于对各种形变类型进行定量分析，将整个绕组的形变程度分别量化为输入变量的不同取值。各输入变量的取值范围由变压器模型的实际几何尺寸和形变程度确定，如表2所示。

表2 输入变量取值范围

2.2 建立响应面模型

考虑到响应面模型的计算精度和复杂程度，选择二阶响应面模型作为初始模型，并通过有限元仿真对CCD试验设计获得的25个样本点数据进行仿真分析，得到样本值，进一步得到响应面模型并校验该模型的拟合度，结果如表3所示。

由表3可知，二阶响应面模型的拟合优度指标及最大误差均不满足精度要求，因此将响应面模型阶数进一步增加到三阶、中心点试验重复次数设置为16，此时采样点数增加到40个(表3)，此时拟合优度指标及拟合精度均满足要求。高频变压器漏感参数随绕组形变的响应面模型为

表3 响应面模型拟合度及误差分析

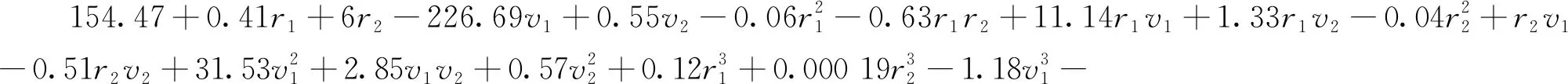
(11)

2.3 响应面模型精度分析

为了更直观地体现出响应面模型在整个取值范围内的拟合效果，假定只有其中一个输入参数发生变化，并在输入变量取值范围区间内随机取值，通过参数化有限元仿真得到漏感参数的仿真值和响应面模型计算值随该变量变化的曲线，如图6所示。可以看出：①以参数化有限元仿真结果为参照，三阶响应面模型的计算精度高于二阶响应面模型，其最大误差分别为0.26%、0.36%、0.32%和 0.17%；②实际中，副边绕组受到的是向内压缩的径向力和轴向压力，而原边绕组是受到向外扩张的径向力和轴向压力，绕组产生相应变形后都会使高频变压器的漏感参数增大，这将影响高频变压器两端变换器的输出效率；③在这4种类型的绕组形变中，原边绕组发生径向形变时，对高频变压器的漏感参数的影响最大。

图6 响应面模型拟合精度对比

3 全局灵敏度分析

3.1 Sobol’法基本原理

基于上述分析得到的三阶响应面模型，选择采用Sobol’法对其进行全局灵敏度分析。该方法是一种基于方差的蒙特卡洛法[20]，其核心思想是：在输入变量域In={x|0≤xi≤1;i=1,2,…,n}内，将函数f(x)分解成2n项之和，如式(12)所示，再通过随机采样计算函数f(x)的总方差及各分项的偏方差，进而计算出响应面模型的灵敏度系数。

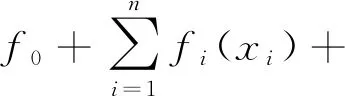
(12)

式(13)中：f0为常数项；fi(xi)和fi,j(xi,xj)分别为一元函数子项和二元函数子项。各子项对其所包含任意一变量的积分为零，可表示为

(13)

式(13)中：fi1,i2,…,is(xi1,xi2,…,xis)为is元函数子项；xk为is元函数子项的其中一个变量，s=1,2,…,n。

由式(12)、式(13)可知，式(12)中的所有子项之间都是正交的，即

(14)

因此函数f(x)的各子项通过多重积分计算得到，可表示为

(15)

(16)

fij(xi,xj)=-f0-fi(xi)-fj(xj)+

(17)

同理，即可求得函数f(x)的其他高阶项。将式(12)两边平方并在整个变量域In内积分得

(18)

函数f(x)的总方差D为

(19)

s阶偏方差为

(20)

由式(18)～式(20)可得

(21)

因此，函数f(x)的全局灵敏度系数可表示为

Si1,i2,…,is=Di1,i2,…,is/D

(22)

Sobol’法的一阶灵敏度系数反映的是单个变量发生变化时，对函数f(x)输出结果产生的影响；而全局灵敏度不但反映了单个变量发生变化时产生的影响，还考虑了各个变量交互作用后对函数f(x)输出结果的影响。若某变量灵敏度系数越接近于1，则表示函数f(x)对该变量的灵敏度越高。

3.2 全局灵敏度分析结果

基于上述得到的三阶响应面模型，将响应面模型与Sobol’全局灵敏分析方法相结合，在表2的基础上，利用蒙特卡罗法抽样方法对各个变量进行随机采样。分别从0～3 000范围取了17个不同数量的采样点。结果表明：对于一阶灵敏度系数，当采样点个数2 500时，结果基本趋于稳定；对于全局灵敏度系数，当采样点个数达到超过600时，结果基本趋于稳定，如图7、图8所示。

图7 一阶灵敏度系数

图8 全局灵敏度系数

因此为了分析结果的正确性和合理性，选择在各变量的取值范围内，采用蒙特卡罗抽样方法对各参数进行随机采样，采样点个数为3 000，计算得到各采样点的漏感参数大小，最后利用Sobol’法计算各变量的一阶灵敏度系数、全局灵敏度系数以及各变量的贡献度，计算结果如表4所示。

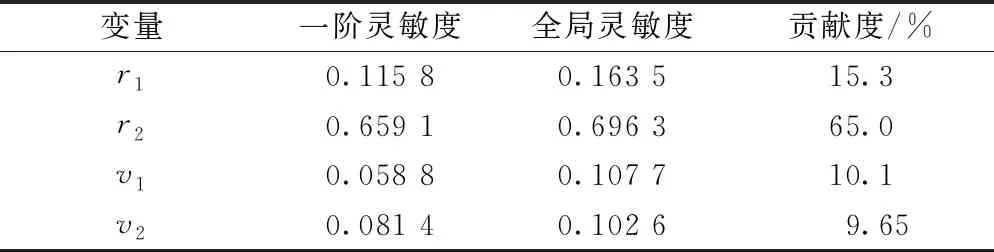
表4 灵敏度分析结果

为了更加直观地说明各变量变化对高频变压器漏感参数的影响程度，绘制了各变量的灵敏度系数柱状图和贡献度饼状图分别如图9、图10所示。

图9 各参数的一阶灵敏度和全局灵敏度

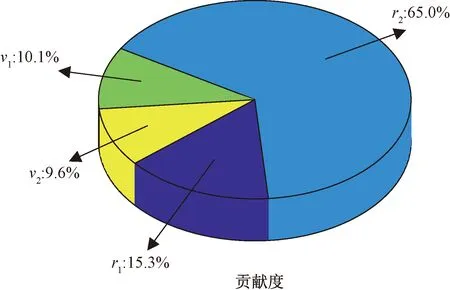
图10 各参数的贡献度

分析可知，高频变压器漏感参数对4个输入变量的灵敏度不同，且差异较大。其中该参数对原边绕组内半径r2的灵敏度最高，为0.696 3；其次是副边绕组内半径r1，其灵敏度为0.163 5；而对副边绕组匝间距离v1和原边绕组匝间距离v2的灵敏度较低，分别为0.107 7和0.102 6。分析结果可知：①绕组发生径向形变对高频变压器漏感参数产生的影响比纵向形变大；②高频变压器漏感参数对原边绕组径向形变最灵敏。

综上所述，应用Sobol’法计算可以得到不同形变类型对漏感参数影响程度的定量结果，且同时考虑了绕组发生复杂形变时各变量间交互作用对漏感参数的影响。此外，由分析计算结果可知，原边绕组径向形变对高频变压器漏感参数的影响最大，且远高于其他类型的形变。因此，在对高频变压器进行结构设计时，应重点关注原边绕组的径向稳定性。同时，可将漏感参数引入绕组形变的检测判据中，为高频变压器的形变检测提供依据。