铁路注浆工程中浆液扩散规律研究

孙宏伟

中国铁路设计集团有限公司，天津 300308

随着我国铁路工程建设的快速发展，很多已建及在建的铁路面临软土地基、富藏地下水地层、含泥软弱破碎带等不良地质问题，由此造成的隧道渗漏与突水突泥、路基变形沉降过大等工程病害严重影响我国铁路工程基础设施的安全服役性能。注浆技术以其设备轻巧灵活、施工技术成熟、环境影响程度小等优势广泛用于铁路各类工程病害的治理。由于现有注浆技术不易控制注浆量、注浆压力、浆液流向、凝固时间、补强位置等参数，造成了注浆效果难于预测。因此，注浆过程中浆液扩散机理的研究至关重要［1-5］。

注浆理论发展远远落后于注浆实践，目前关于浆液扩散范围等的理论公式研究远未成熟［6-7］。大部分计算浆液在孔隙裂隙中的渗流理论都会对被注介质孔隙裂隙进行一定程度的简化，故难以反映真实扩散情况，而且大多经验公式都是由特定地质条件推导得出的，不具有普遍意义。完善注浆浆液扩散理论具有十分重要的理论意义和实践价值。同时，模拟是注浆理论研究的常用手段，快捷高效的理论模型能为优化浆液用量、科学设计注浆压力等提供依据。传统模型由于非线性的存在，其计算效率并不乐观，导致在有数百条裂缝的复杂裂缝岩土体网络中模拟注浆渗透过程需要相当长的时间，实用性较差。

本文基于研发的超大规模土颗粒-浆液动力耦合作用的并行流固耦合仿真分析程序，系统考虑浆液特性、注浆压力及岩土体力学特性，从微观层面揭示土体介质及水灰比对浆液扩散的影响规律，建立浆液在砂土、黏土和角砾土等介质中扩散范围的理论公式，并利用自主研制的独立变频变压注浆模型试验装置进行试验验证。

1 劈裂注浆仿真分析模型

针对大规模颗粒-流体动力耦合计算（颗粒数大于等于4万）的难题［9-11］，以颗粒-流体间的相互作用力和变形为载体，通过流体湍流数学方程和颗粒动力学方程，系统构建了流动场内颗粒的曳力模型（图1），实现颗粒位置、速度、受力及变形等信息的动态更新。

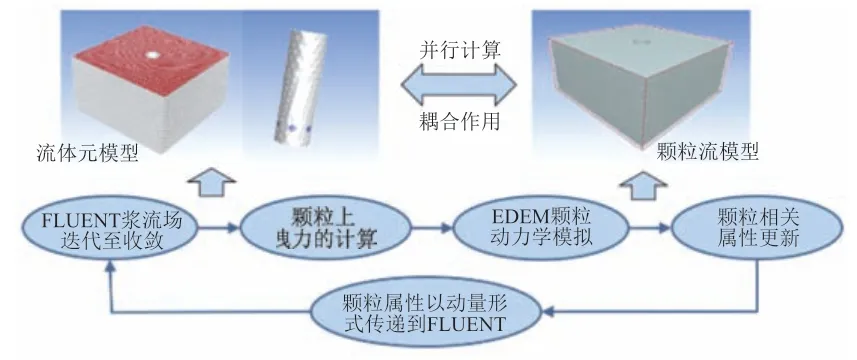
图1 土颗粒-浆液动力并行流固耦合仿真程序

本次仿真分析主要涉及到砂土、黏土及角砾土，具体力学参数见表1。

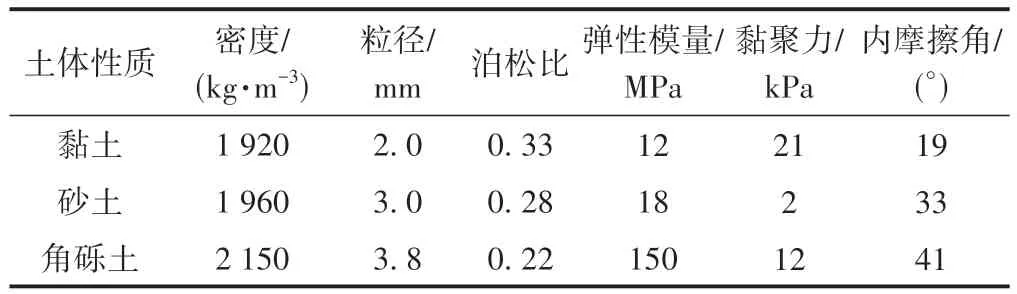
表1 土体力学参数

建立砂土、黏土、角砾土介质的计算模型，见图2。砂土介质模型长60 cm，宽60 cm，高10 cm；黏土介质模型长70 cm，宽70 cm，高10 cm；角砾土介质模型长100 cm，宽100 cm，高15 cm；注浆管半径为4 cm。为了模拟真实注浆情况，在注浆管距底部4 cm 处对称设置6个注浆孔，注浆孔半径1 cm。模型四周为墙体，不允许颗粒从模型内部逃出。

图2 计算模型

根据实际工程要求，模拟7 个不同注浆压力作用下接触键的破坏，注浆压力分别为0.10、0.15、0.20、0.25、0.30、0.40、0.50 MPa。

2 注浆模拟结果分析

2.1 土体介质影响

颗粒之间受外力破坏的接触键可直接显示，利于研究颗粒之间接触键的破坏规律。接触键破裂密集的范围可以视作劈裂区，此范围的土体受到浆液的冲击作用和劈裂作用，使土体的接触键破坏得更集中，更彻底。在劈裂区外围，由于浆液的作用效果较小，浆液对土体的作用力变小，故形成了挤压区。该区域土体颗粒之间的接触键破坏的范围更大，但是区域接触键数量比劈裂区少。

注浆压力为0.1、0.2、0.3 MPa时三种土体介质的二维平面接触键破裂见图3。可知：三种土体介质对扩散范围的影响基本一致；岩土体介质的孔隙率越大，浆液的扩散半径越大，浆液在角砾土介质中的扩散半径最大，在黏土介质中的扩散半径最小。

图3 二维平面接触键破裂

2.2 注浆压力影响

1）砂土介质

相同注浆时间下，不同注浆压力时砂土的三维整体破坏范围见图4。可知，注浆压力的增大使得浆液对土体的破坏范围增大。

图4 不同注浆压力时砂土三维整体接触键破裂情形

不同注浆压力砂土的接触键破坏效果见图5。可知：浆液对土体的破坏效果呈碗状，即在底部注浆孔处，从下到上，土体的破坏范围越来越大，且随着注浆压力的增大，碗的直径也越来越大。这是由于浆液对土体的冲击作用使土体的承载能力受到了影响，从而影响了模型上部结构的微型接触键，并且在注浆压力0.4 ～0.5 MPa 时，整个模型均受到了影响，使得整个土体中的接触键都开始发生了破坏。这说明在注浆压力过大时，注浆反而不能增强土体承载力。

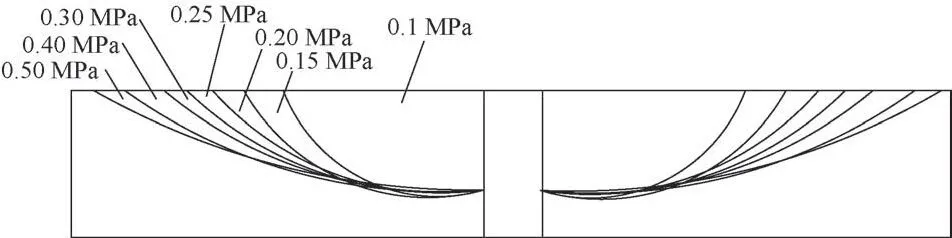
图5 各个注浆压力的接触键破坏效果

将不同注浆压力作用下的土体颗粒接触键的破坏效果导入到CAD中，并统计出浆液劈裂半径（图6），从而得到不同注浆压力下的劈裂区范围。

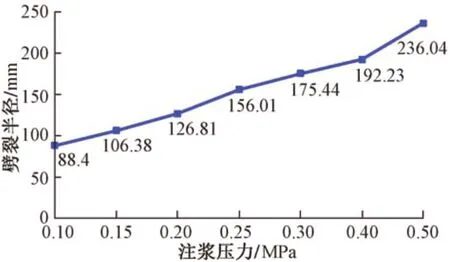
图6 各个注浆压力时砂土的劈裂半径

由图6 可知：砂土的劈裂半径与注浆压力间的关系曲线呈指数分布，说明注浆压力的增大使得劈裂半径也增大。

2）黏土介质

由于黏土介质中土体之间的接触力设置比其他两种介质更大，故在注浆压力较小时（0.10～0.25 MPa）浆液破坏效果并不明显，而在注浆压力较大时（0.3 ～0.5 MPa），土体之间破坏程度开始加大。这也符合浆液土体作用的一般规律。相同注浆时间下不同注浆压力时，黏土的二维整体破坏范围与砂土一样。

对7 种注浆压力下接触键的破坏程度进行分析，得到黏土劈裂半径，见图7。可知：黏土的劈裂半径与注浆压力的关系曲线与砂土类似，土体的劈裂半径随注浆压力的增大而增大，且存在一定的函数关系。

图7 各个注浆压力黏土的劈裂半径

3）角砾土介质

相同注浆时间不同注浆压力下角砾土的接触键破坏规律与砂土、黏土一致，但浆液对角砾土体的破坏范围比其他两种土更加明显。整体的接触键的破坏也是由注浆孔开始，随着注浆压力的增大，逐渐向模型的边界延伸。不同注浆压力下角砾土的劈裂半径见图8。

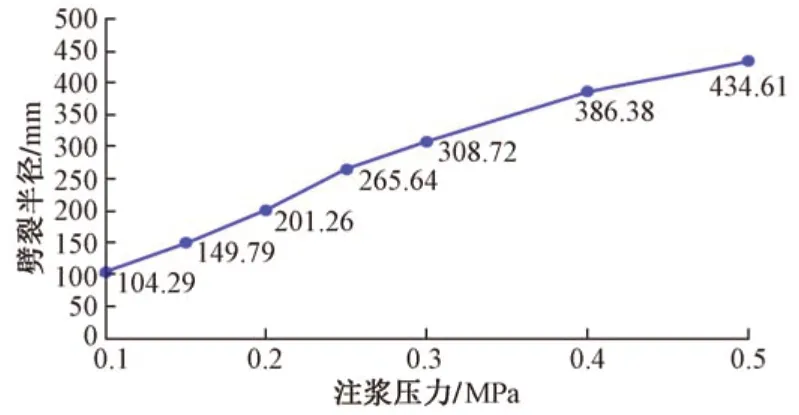
图8 各个注浆压力的劈裂半径

综上所述，三种介质中浆液的扩散半径均随着注浆压力增大而增大，且随着注浆压力不断增大，其扩散半径的变化速率越来越快。

2.3 浆液参数的影响

灰水比选取 0.6∶1、0.8∶1、0.9∶1 和 1∶1 共 4 种工况。

1）砂土介质

不同浆液灰水比时砂土劈裂半径见图9、图10。可知：不同浆液的灰水比时，砂土的劈裂半径也不同。随着浆液灰水比增大，砂土的劈裂半径逐渐减小。

图9 不同灰水比劈裂半径三维变化图

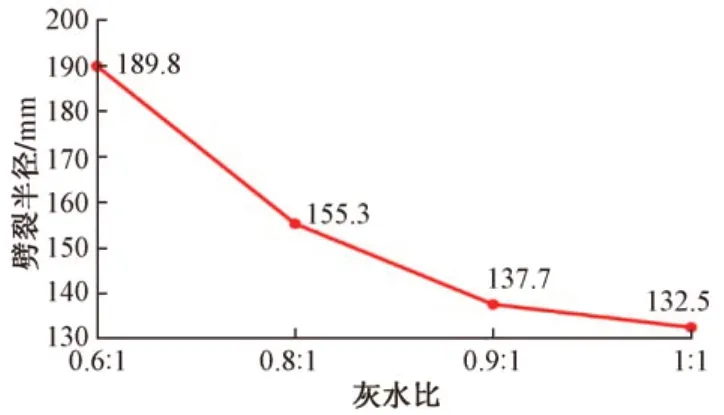
图10 不同灰水比劈裂半径

2）黏土介质

与砂土的模拟结果类似，随着浆液灰水比的增大，其劈裂半径减小，说明在黏土体中注浆与在砂土体中注浆所表现出的规律一致，都与注浆浆液的密度有直接关系。

3）角砾土介质

与砂土、黏土的模拟结果类似，但其浆液的整体破坏范围是大于其他两种介质。

3 浆液扩散范围计算方法

构建浆液在砂土、黏土、角砾土三种介质中扩散范围量化计算模型。模型中，x₁为注浆半径；y₁为射浆孔半径；b为注浆管半径；R为土体微观层面接触键破坏范围半径，R=15.204p1.418+b，P为注浆压力。

浆液在砂土中扩散计算公式为

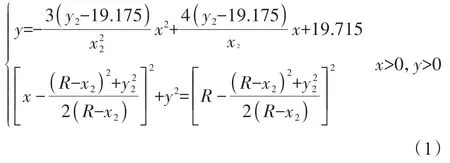
浆液在黏土中扩散计算公式为

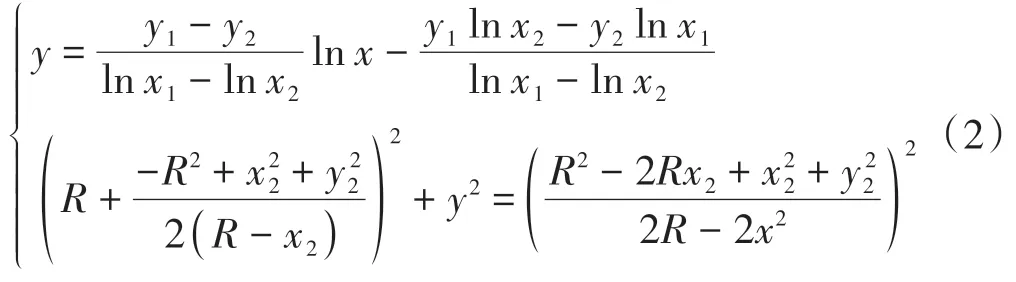
浆液在角砾土中扩散计算公式为

4 模型试验

自主研制了高压变频注浆模型试验装置，见图11。通过研发浆液压力自感应传感器及其自适应补偿装置、注浆管定位构件等解决了注浆模型试验中注浆管高压扰动、压力-流速耦合联动等技术难题。

图11 高压变频注浆模型试验装置

利用该装置对砂土进行注浆模型试验，试验结果见图12（a）。将试验过程中注浆半径、注浆管半径等参数带入砂土介质中浆液扩散计算公式中，计算结果见图12（b）。模型试验结果与计算结果中，相同注浆压力下浆液扩散半径值基本吻合。验证了浆液扩散计算公式的准确性。

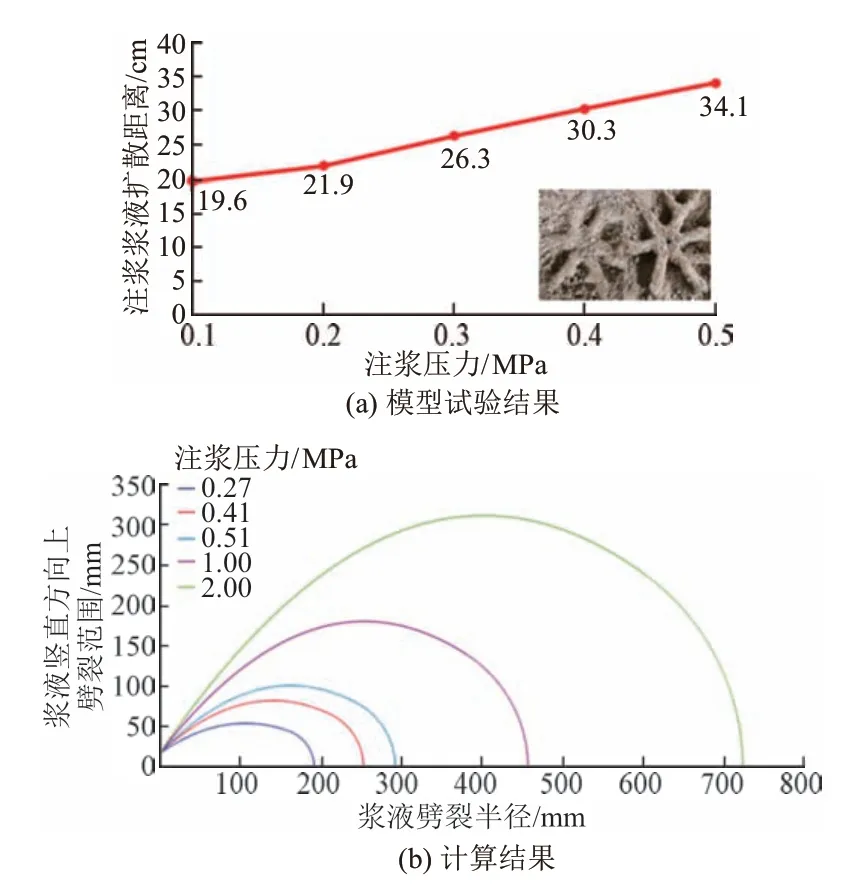
图12 砂土介质浆液扩散试验结果及计算结果

5 结论

1）自主研发了超大规模土颗粒-浆液动力耦合作用的并行流固耦合仿真分析程序，系统揭示了浆液在砂土、黏土、角砾土3 种不同岩土介质中的扩散规律，定量刻画了浆液扩散半径的花瓣形分布。

2）分析了浆液在砂土、黏土、角砾土3种不同类型岩土介质中的扩散规律，从微观层面确定浆液水灰比、注浆压力等注浆参数对浆液扩散半径的影响，低水灰比、高注浆压力条件下可实现更大的注浆范围。揭示了高压浆液对岩土介质的渗透-耦合加固机制。

3）基于自主研发的高压变频注浆模型试验装置进行室内试验，验证了砂土介质中浆液扩散量化计算模型正确性，指导工程设计与注浆加固方案优化，为实际工程中注浆范围、注浆量的确定提供理论基础，有力支撑了高速铁路基础设施注浆扩散机理研究。