离心泵调速时流量关于扬程和转速的回归分析

方清华

（江汉大学智能制造学院，武汉430056）

随着变频调速技术的发展，其在离心泵调速控制中的应用也越来越广泛。在离心泵运行过程中，需要对其进行实时变速调节控制时，可以由所需要的流量和扬程来预测并确定调节所需要的转速[1]，但也常常需要确定在扬程和转速变化后的流量是否达到预期值，这就需要寻找流量随扬程和转速变化的函数关系式，用来随时准确地确定离心泵变速调节时的流量。本文用数理统计的方法，对离心泵变速调节运行时的流量、扬程和转速的实测数据进行分析，得到了流量Q与扬程H、转速n之间的相关关系，可以用其方便地由扬程和转速预测变速调节时所得到的流量。

1 数学模型的建立

在离心泵进行变速调节时，其扬程H、转速n和流量Q之间会有如下的函数关系：

采用多元指数的形式来创建经验公式[2]，则（1）式可以表达为：

式中：Q——流量，m3/h；

H——扬程，m；

n——泵转速；

k、a、b——常数

对式（2）取自然对数，可得：

设y=lnQ，x1=lnH，x2=lnn，k0=lnk，则式（3）可变换为：

由实测的36组实验数据，按照式（4）函数关系回归计算可得：

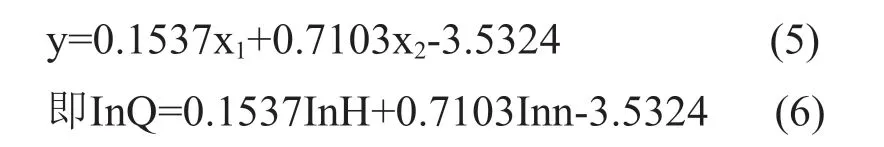
回归方程的相关系数R2=0.9994，计算结果见表1、2、3所示。

表1 方差分析

2 数学模型的检验

2.1 相关性检验

当显著性水平α=0.05时，置信水平为1-α=0.95，由前述回归过程可知变量数为2，N=36,则其自由度是N-2=36-2=34，查表[3]得到R临=0.325。表2计算结果R=0.9996，所以有R＞R临，由此可认为在α=0.05时，y与x1、x2，即lnQ与lnH、lnn之间具有良好的统计相关关系，即式（5）、（6）成立。另外，因为R=0.9996，趋近于1，也说明lnQ与lnH、lnn之间就是完全相关的。

表2 回归统计

2.2 显著性检验

采用F检验法对回归方程进行显著性检验。当α=0.05、变量数为2和N=36时，查表[3]得到F的临界值为3.29，表1中计算结果F0=26642，所以有F0》F临，故可认为y关于x1、x2，即lnQ关于lnH、lnn的回归效果是非常显著的。

2.3 回归线的精度

从表2的计算结果可知，回归方程的标准误差S=0.008744，此S值较小，也说明了回归线的精度比较高

2.4 t检验

当α=0.05、变量数为2和N=36时，查t分布表[3]得到t临=2.035，表3中的计算结果， t0=-15.7474，t1=7.2056，t2=19.7224，由于t0、t1和t2的绝对值都大于2.035，所以，x1、x2对y，即lnH、lnn对lnQ均有显著的影响。

表3 回归结果

3 Q关于H、n的回归方程

由前述方法求得y关于x1、x2，即lnQ关于lnH、lnn的线性回归方程如下：

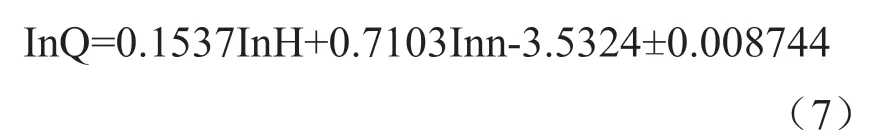
式（7）中有k0 =-3.53244= lnk，可计算得到：k=0.02922，所以式（6）可转换成：

式（8）就是离心泵变速调节时，其流量Q关于扬程H和转速n的非线性回归方程。

4 变速调节时流量Q的预测

4.1 点预测

使用式（8）可以根据扬程H和转速n的取值对流量Q进行预测。例如，当H=15.0m，n=2410转/min时，计算得到Q=11.19m3/h，实测值则是11.15m3/h，计算误差为0.359%。由此可见，式（8）计算得到的流量Q与实测值很接近，误差非常小，说明由式（8）计算的预测值准确度较高。

4.2 区间预测

在需要离心泵的扬程和转速保持一定的值时，可以对流量Q进行区间预测。比如，当H=15.0m，n=2410转/min时，采用式（6）计算得到1nQ=2.4152。根据表2的结果，S=0.008744，则有：Δ=t0.05/2(36-1)×S=2.035×0.008744=0.01779。

预测区间由下式所示：

将前述得到的计算值代入并计算可得： 10.99＜Q＜11.39，点预测值Q=11.19m3/h刚好落在计算得到的区间内。

5 结论

5.1 离心泵变速调节时，流量Q和扬程H、泵转速n之间具有非线性相关关系，其回归方程如式（8）所示。

5.2 利用式（8）可以对变速调节时的流量Q进行预测。