直升机释放无人机的选址问题研究

李松锐 张 明 王蒙蒙 李伯权 裴正莹

(南京航空航天大学民航学院 南京 211106)

0 引 言

在以往研究中提到无人地面车辆(unmanned ground vehicle ,UGV)-无人机(unmanned aerial vehicle，UAV)基于协作搜索的路线规划方法[1-3]，UGV作为无人机的“能源服务站”，以补充无人机电量.在满足UAV电池能耗约束的前提下，以UAV的总距离最小、UGV的总距离最小及其二者总和最小作为优化目标进行求解，从而获得协同任务计划结果.但是，这种方法规模较小，没有考虑地形和环境因素对结果的影响，而是在2D平面内建立模型.Maini等[4]建议使用移动加油站扩大操作范围，这可以节省空间和时间成本.尽管已经考虑了地形对移动加油站位置的影响，但该文献在实践中在飞行任务分配方面仍存在某些不足.

在一些研究中，无人机的飞行路径通常是理想的，而没有考虑到无人机避开地形障碍和天气、无人机的性能、无人机的释放和回收，以及无人机在实际任务的不同飞行阶段中的能耗差异的影响进行分配[5].没有探讨无人机的电量限制[6].无人机在搜救点的盘旋过程通常与灾区状况的严重性有关[7].搜救点的等级属性分离是一个灾害分级问题[8].因此，必须进一步结合救援实践来考虑无人机的灾害分分级与悬停时间之间的相关性.

在以往的研究中，优化的目标通常为整体的路径最短，但在文中研究的无人机和通航直升机协同搜救中，通航直升机的速度远远大于无人机并且通航直升机的能源一般较为充足，为使得救援效率提高，优化的目标不再是整体路径最短，而着重考虑无人机的电量消耗对搜救过程中的影响.

1 问题描述

由于应急救援中考虑对搜救点进行分配之前，需要对通航直升机释放无人机的位置进行选址，建立适合本文情景的选址模型，考虑地形和低空风对无人机电池能耗的影响，以及悬停与飞行状态的能耗差异等因素，以搜救的费用最小为目标进行建模，并运用改进二进制蝙蝠算法进行求解.

获取无人机性能数据(包括最大续航时间、最大悬停时间、3级低空风对无人机电池能耗的影响下的飞行续航时间、升限、价格、最大充电次数等)、所研究地区地形数据，以及主要的八项灾情指标；考虑无人机飞行续航性能、灾情等级、风和地形对无人机续航时间的影响，以总的搜救费用最小为目标，对通航直升机释放无人机位置的确定问题进行建模.对二进制蝙蝠算法改进，引入差分进化机制，对上述模型进行求解，确定通航直升机释放无人机的位置，并与未改进的算法求得的结果进行对比分析.

2 直升机释放无人机位置点选址模型

2.1 模型假设

1) 备选的通航直升机悬停点位置、无人机的目标搜索点的具体坐标已知，各节点之间的距离按照欧氏距离计算.

2) 将考虑低空风对无人机电池能耗的影响、避障的影响及悬停影响下的能耗换算成无人机在不考虑以上因素匀速飞行状态时(如本文算例中机型A的速度为15 m/s)对应的航程进行计量.

3) 搜救高度相对目标搜索点的地形高500 m.

4) 每个目标搜救点有且仅有一架UAV进行搜索.

5) 各节点出发的UAV的速度均一致，无人机的航程成本与无人机完成任务换算成的航程成正比.

6) 不考虑无人机充电即多次循环使用问题，发射前为满电量.

7) 根据通航直升机在山区的最低安全高度要求标准，其释放无人机的位置的相对地面高度不得小于600 m.

8) 不考虑无人机的通讯问题，数据传输效果在任何飞行位置均为良好.

2.2 参数定义

选址模型变量为：M为备选通航直升机释放无人机位置集合，M={1,2,…,m,…,|M|}；N为无人机目标搜索点集合，N={1,2,…,n}；Fj为释放位置j的服务费用，元；djk为从释放位置j到目标搜救点k的欧式距离，m；c为UAV单位飞行距离的成本，元/m；tk为UAV在目标搜索点k的悬停时间，s；D为UAV的最大行驶里程(以无人机续航时间计算)，m；α为低空风对电池能耗影响系数；β为避障能耗预留率；γ为旋翼无人机飞行与悬停能耗比；l为计划选取的通航直升机释放无人机位置的个数；v为无人机匀速飞行的速度，m/s；Sjk为考虑风和避障的条件下无人机从第j个通航直升机悬停点到第k个搜救点完成搜救任务的能耗换算成不考虑外界因素的理想状态下无人机匀速飞行的航程，m；xj为备选中心j被选中则为1，否则为0；zjk为搜救点k由备选中心j服务则为1，否则为0.

2.3 模型建立

考虑无人机的性能参数，分别求解低空风对电池能耗影响系数、旋翼无人机飞行与悬停能耗比.设满电量条件下UAV在无风条件下的最大悬停时间为Thover，以速度v可以飞行的最大时间为Tv，无人机一般适合在某级风以下的条件进行飞行活动，设在该级风条件下(如本文所研究的无人机机型适合长时间在3级以下的风场中飞行，需要预留足够的能量)无人机最大飞行时间为Twind，则无人机飞行与悬停能耗比和低空风对电池能耗影响系数分别为

(3)

(4)

目标函数：

(5)

约束条件：

(6)

(7)

zjk≤xj，j∈M,k∈N

(8)

(9)

Sjk≤D,j∈M,k∈N

(10)

zjk={0,1},j∈M,k∈N

(11)

xj={0,1},j∈M

(12)

式(5)为目标函数，表示总的搜救代价最小，包括总的完成搜救的费用(飞行和悬停)和总的服务费用；式(6)为每个搜救点由通航直升机在释放无人机的位置点处派出一架无人机进行搜救；式(7)为从备选通航直升机释放无人机的位置点中最少选出l个释放位置点进行无人机的释放；式(8)为对于搜救点k，通航直升机在释放无人机位置点j派出无人机搜救，则j必须是被选中的释放点；式(9)为在不考虑任何外界条件下以一定速度匀速飞行时为理想状态，则需要将无人机考虑风、避障以及悬停状态等因素下完成任务的能耗换算为理想状态下无人机的航程Sjk；式(10)为无人机悬停点到搜救点的搜救范围约束，表示无人机从通航直升机释放无人机的位置点j到搜救点k完成搜救任务的能耗换算为无人机匀速飞行状态下的航程不大于无人机的最大航程；式(11)和(12)为决策变量zjk和xj是0-1变量.

3 算法设计

将蝙蝠算法(bat algorithm，BA)用于通航直升机释放无人机的选址问题，计算方便且计算效率高，结果更精确.但由于BA本身的缺陷，即主要依靠个体之间的信息交换进行优化，缺乏个体变异的机制，使得求得的解迅速向优秀的个体聚集从而使得求解陷入局部最优[9]，本文引入差分进化算法(differential evolution algorithm，DE)，使得蝙蝠个体产生变异，对二进制蝙蝠算法(binary bat algorithm，BBA)作出改进，进而得到更优的解.

1) 编码方式设计及种群的初始化 初始化种群中是有d个备选位置选出l个释放位置，则d为每个蝙蝠的维数.对于式(9)，令α2和αk分别为

(13)

αk=αγtkvi，k∈N，i∈W

(14)

对于第k个搜救点，tk已经确定，则知αk为常数.α2显然是常数，用第i类无人机搜索时，vi也是定值，则式(9)可以简化为

Sjk=α2djk+αk,j∈M,k∈N

(15)

由式(15)可知，无人机由于悬停而产生的总费用与释放位置的选择有关，因而一旦确定释放位置，即可采用就近分配的原则将搜救点分配给离其最近的释放位置.如从10个备选位置中随机选择7个释放位置，被选中的序号位置置1，其余置0，则其中一个蝙蝠可以编码为[1,1,1,0,1,1,0,0,1,1]T，表示第1,2,3,5,6,9,10号释放位置开放，而其他释放位置关闭.释放位置确定之后，搜救点采用就近分配并且满足约束条件则任务即分配完毕，否则该蝙蝠停止向此次方向进化，取父代继续向其他方向进化.

2) 评价函数的定义 评价函数Evaluation这里取目标函数的值，即式(16)，其数值越小，个体越优良.

(16)

3) 改进的二进制蝙蝠算法(improved binary bat algorithm，IBBA) DE拥有更多丰富的突变策略，其突变算子更有效地利用了种群分布特征，并且突变效率更高.使得DE和BBA的结合可以克服BA的收敛精度低，容易陷入局部最优等缺点.应当注意，DE算法也是一种连续优化算法，因此将其转换为二进制DE.

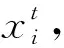
(17)

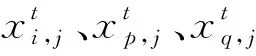
从总体中随机选择两个与当前个体不同的个体；然后，将它们之间的差分向量加到当前最优个体上，差分突变后的新个体的分量可以表示为

(18)

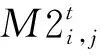
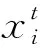
(19)

4) 改进二进制蝙蝠算法步骤

步骤1随机生成规模为d，维度为d的初始解.最大脉冲音量r0，最大脉冲率r0，最大迭代次数Ngen.根据评价函数值的大小寻找当前所有蝙蝠个体中的最优解.

步骤2蝙蝠i的搜索脉冲频率fi更新方式如式(20)，其中fmin和fmax分别为最小和最大搜索脉冲频率，β1是均匀分布的随机数，β1∈[0,1].

fi=fmin+(fmax-fmin)β1

(20)

标准蝙蝠算法求解是用来求解连续型函数的优化问题，所以需要对蝙蝠的位置更新公式以及速度更新公式进行变换，得到适合求解离散优化问题的BA.对标准BA进行修改，得到BBA.所求的目标为最小化，为将寻优域维持在0-1两个数内，对蝙蝠的速度变换和位置变换为

(21)

(22)

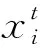
步骤3生成均匀分布随机数rand，如果rand>r(r为蝙蝠游走步长)，则对x*进行随机扰动，产生一个新的解，并对新的解根据式(23)进行越界处理，其中rand(1,d)代表生成d维0-1之间的随机数.

xnew=∧(xold,round(rand(1,d)))

(23)

(24)

(25)

步骤5变异和交叉

步骤6对当前全部蝙蝠个体的评价函数值排序,得到当前最优解.

步骤7重复步骤2～步骤6直至达到最大迭代次数.

步骤8输出全局最优值和最优解.

4 算例分析

4.1 数据获取

选用三种不同机型进行分析，其性能数据见表1.

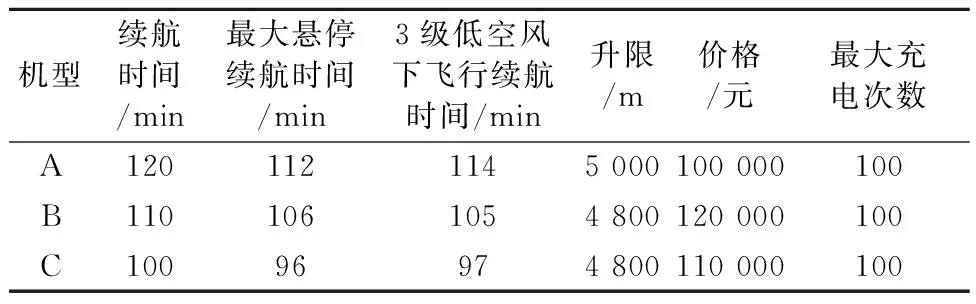
表1 无人机性能参数

文中所用机型A无人机型号为多旋翼类型无人机X6L(双电池)，以飞行速度15 m/s进行计算，其最大航程为108 km.机型B为X6M(双电池)，机型C为Z6M(双电池).风的折算和悬停折算可以根据对应公式求得，对于地形的避障，根据实际地形情况取折损系数，在这里取30%.

4.2 模型及算法参数

算例分析中用到的模型参数和算法参数见表2.

表2 机型及算法参数设置表

4.3 基于改进二进制蝙蝠算法的通航直升机释放无人机位置选址

释放位置有100个备选，根据通航直升机山区飞行最低高度最少要位于障碍上方600 m处，则选取释放位置位于释放点高程上方600 m处进行无人机的释放，保障通航直升机的飞行安全，备选点的经纬度坐标与搜救点一致，高度在搜救点(相对地面高度500 m)的基础上增加100 m.

1) 种群初始化 以机型A为例，机型B和C类似.产生全1序列，长度为100，为便于后面进行迭代使得开放位置越来越少，随机取其中一个位置置为0，则其中一个蝙蝠可以为[0 1 1…1]，以同样的方式产生其余蝙蝠，选取释放位置的个数不少于18个.

2) 计算结果 运用IBBA进行迭代800次，分别与BBA、二进制粒子群算法(binary particle swarm optimization，BPSO)[10]、简化的二进制人工鱼群算法[11](simplified binary artificial fish-swarm algorithm，S-bAFSA)的迭代结果进行对比见图1.由图1可知:见IBBA算法相比于BBA算法得到的结果更优，在保证各相同参数一致的条件下，IBBA算法相比于BBA的总费用平均减少了4.60%，而相比于BPSO、S-bAFSA得到的总费用平均分别减少了21.20%和4.13%.同理，运用机型B和机型C分别进行算例分析，得出IBBA相比于其他算法总费用减少的比率见表4，其中费用变化率见式(26).

图1 IBBA和其他算法迭代效果对比

表3 三种机型选址结果对比

(26)

三种机型的结果中，IBBA相比于BPSO、S-bAFSA、BBA得到的结果的总费用平均减少了22.07%、6.17%、6.61%，表明改进后的算法在求解质量上相比于改进前以及其他优化算法有明显提高.

取IBBA的运行结果进行进一步研究，其对应的解为：[0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 1]，即开放7，13，16，17，25，30，38，39，42，53，61，71，74，75，78，89，91，100号等18个位置作为通航直升机释放无人机的位置，每个释放位置分配搜救点的其中一种结果见表4.

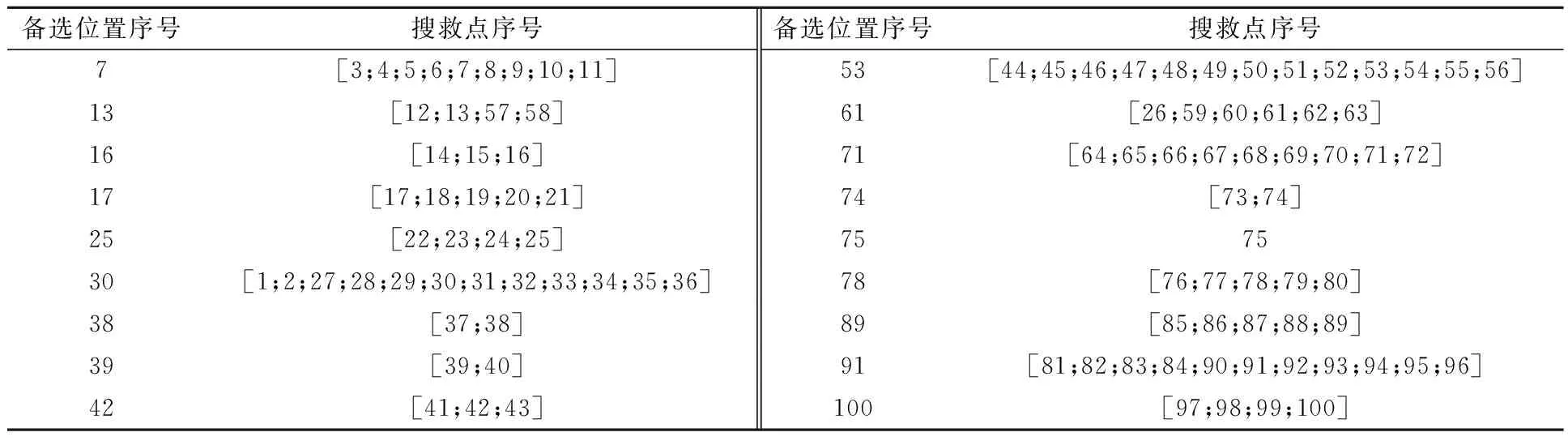
表4 无人机释放点选址结果及对应选址点任务分配结果

5 结 束 语

文中提出了考虑无人机运行环境和性能的通航直升机释放无人机位置选取模型.根据灾区的各项灾情指标，人口分布对受灾搜救点进行模拟，并考虑无人机的探测范围来确定目标搜索点的灾情等级和相应悬停搜救时间.在考虑灾情等级，无人机性能和低空风对无人机电池能耗影响的基础上，建立了通航直升机释放无人机的位置选址模型，引入差分进化机制，改进的二进制蝙蝠算法进行求解，从而得到更优的结果.由于对地形因素避障预留的无人机电池电量难以准确评估，该研究的文献较少，只能以一定的覆盖率来完成搜索任务，未来研究考虑引入无人机电池环境与耗能曲线，精确估计无人机能耗，提高无人机任务分配的准确度.此外，在救援点的高度各不相同，如果无人机在不同的救援和搜索点悬停时改变高度，无人机的能耗状况随之改变，并且即使在相同的环境条件下进行相同的操作，电池寿命或能耗也存在很多不确定性，只能建立一些较为理想化的数学模型，未来可以对其进行更深入的研究.