基于冲突类型差异的航空器场面滑行路径规划

李慧盈 张 明 刘思涵 王蒙蒙

(南京航空航天大学民航学院 南京 211106)

0 引 言

大型机场作为航空运输的枢纽，交通流量大、密度高已成常态化，而多跑道、多航站楼、多机坪进一步增加了机场复杂度，机场场面滑行冲突增加，往往带来航班大规模延误，造成运输资源的浪费[1-2]，同时还伴随着航空器燃油消耗与污染物排放的持续增加[3-4].欧洲航行安全组织(european organization for the safety of air navigation, EUROCONTROL)提出将高级场面活动引导与控制系统A-SMGCS分为四级功能分步实现[5]，其中欧洲民用航空设备组织(european organization for civil aviation equipment)对一级(监视)、二级(控制)功能有详细的规定和解释[6].三级和四级功能主要包括路由规划、引导和冲突解脱等，由于受到场面运行方式[7]、信息共享和决策机制[8]、地面和机载设备[9]等多方面因素的影响，其详细规定和解释仍在不断发展.因此，考虑场面运行冲突的机场场面的航空器路由规划是A-SMGCS亟待解决和完善的重要问题.

目前研究主要在以下两个方面开展：①将基于时间的轨迹管理程序扩展到航空器场面滑行中，通过对航空器四维滑行轨迹优化，减少滑行冲突，从而确保规划的滑行路由在燃油消耗，缩短滑行时间和污染物排放实现最优[10-11]；②构建基于航空器滑行速度曲线生成框架的多目标路由规划.利用多目标优化策略和时间窗算法规划航空器滑行的最优路由.综合上述研究，多集中于控制或生成航空器滑行全过程的速度曲线对滑行时间和滑行路线进行优化，但是航空器在场面滑行遇到不同的冲突类型时，滑行延误时间及对于滑行路径的选择具有差异.因此，对于航空器场面滑行最优化路径的研究，应同时考虑滑行冲突差异以及相应的油耗和排放，才能更进一步保证场面滑行路由规划结果的精确性.

文中通过在冲突易发生区域设置冲突点，构建航空器场面滑行的交叉冲突、对头冲突和追尾冲突的运动学模型，分析不同冲突类型下航空器速度曲线，并基于上海浦东机场场面信息对航空器滑行路径进行多目标优化分析.

1 场面滑行过程冲突模型

1.1 三类交通冲突下速度曲线模型

航空器在场面的滑行过程可分为无冲突情况以及分别遇到追尾、交叉、对头三种冲突类型的情况，不同情况下航空器的滑行速度曲线会有差异，无冲突情况下的速度曲线约束条件公式见文献[11]，本文重点推导航空器遇到不同冲突类型下的速度曲线公式.

1) 交叉冲突 当两架航空器陆续通过同一个滑行道交叉节点且低于最小安全间隔标准，两机之间将产生交叉冲突，见图1a).航空器1首先通过节点A，航空器2之后通过交叉口A.此时，航空器2的滑行过程可以分为三个不同的滑行阶段：分别是快速制动、停止等待和加速阶段，其速度曲线见图1b).

(1)

d1的界限可以通过航空器2的初始滑行速度v0确定，为了避免冲突，d1的取值范围为

(2)

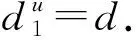
第三阶段的加速度a2，上限为最大加速度amax，a2的取值范围为

(3)

固定了a2之后，得到d3的取值范围为

(4)

2) 追尾冲突 当两架航空器在同一段路径上朝着相同方向滑行时，由于后机的滑行速度高于前机，导致两机之间的滑行间隔低于规定的安全标准，因此两机之间将产生追尾冲突，见图2a).航空器1由节点A滑行至节点C，航空器2紧跟前机滑行.为了解脱追尾冲突，需要控制航空器2进入节点A的时间，并规定其滑行速度不能高于前机以及保持规定的安全间隔.航空器2在滑行阶段遇到追尾冲突时，它的滑行过程可以分为三个不同的滑行阶段：分别是制动、以恒定速度行驶和加速阶段，见图2b).

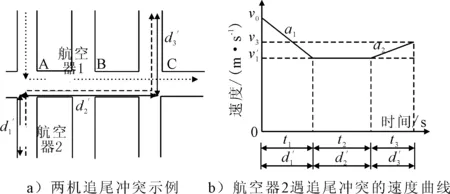
图2 追尾冲突

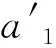
(5)

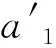
(6)

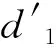
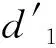
(7)

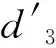
3) 对头冲突 当两航空器在同一段滑行路径具有相反的滑行方向，如果没有其他可以避让线路时，两机之间将会发生对头冲突，见图3a).航空器1先通过滑行段AC，航空器2后通过滑行段CA.为了避免对头冲突，应首先比较两机进入滑行段的时间，再采取先到先服务，令后机(航空器2)到达节点C的时间晚于前机通过节点C.航空器在滑行阶段遇到对头冲突时，它的滑行过程可以分为三个不同的滑行阶段：分别是快速制动、停止等待、加速阶段，见图3b).

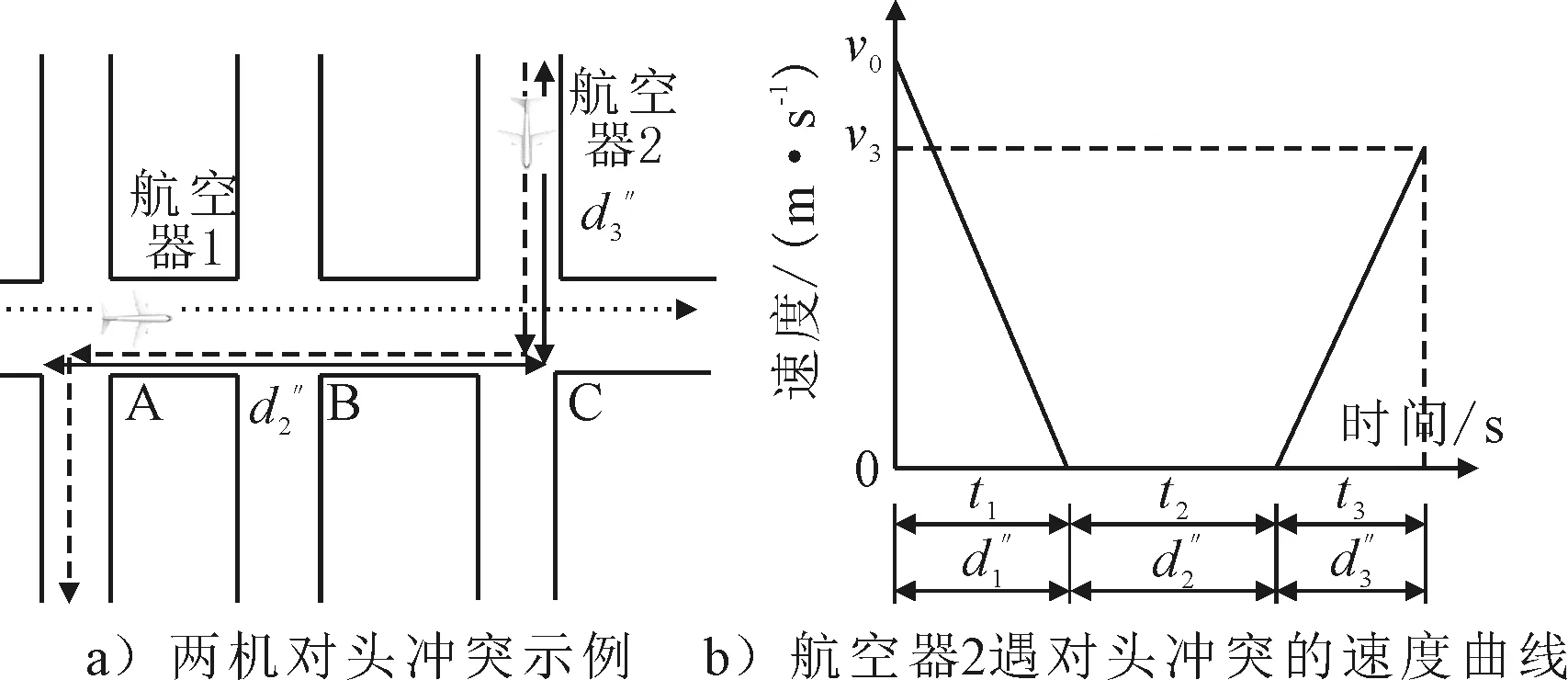
图3 对头冲突

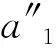
(8)

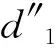
(9)

(10)

(11)

1.2 冲突次数统计

根据实际情况可知，航空器在场面滑行时遇到对头冲突、交叉冲突和追尾冲突为随机事件.由1.1可知遇到交叉冲突的延误时间由另一架航空器通过该滑行道交叉口的时间决定，遇到追尾冲突和对头冲突的延误由另一架航空器通过该滑行道的长度决定.因此估计航空器

(12)

式中：t4、t5、t6分别为航空器遇到交叉冲突、对头冲突和追尾冲突产生的延误时间；β1、β2、β3分别为航空器遇到交叉冲突、追尾冲突和对头冲突次数占总的冲突次数的比值.根据1.1得到t4、t5、t6的计算公式为

t4=s1/v0

(13)

(14)

t6=s3/v0

(15)

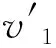
(16)

每种冲突类型的比值乘上遇到冲突的总次数即为遇到每种冲突类型的次数.

1) 交叉冲突次数 航空器滑行过程遇到交叉冲突都是在滑行道交叉口产生的，因此不同滑行路径上交叉口个数的差异决定了遇到交叉冲突次数的不同.机场滑行道系统的总交叉口个数为m0，选择滑行路径qξ的交叉口个数为mξ，因此航空器选择滑行路径qξ的交叉冲突次数为

(17)

2) 追尾冲突次数 滑行路径的长度决定了追尾冲突和对头冲突产生的次数.机场场面滑行路径的总长度为D，选择滑行路径qξ的长度为dξ，因此航空器选择滑行路径qξ的追尾冲突次数为

(18)

3) 对头冲突次数 同理可得航空器选择滑行路径qξ的对头冲突次数为

(19)

1.3 滑行路径优化目标及约束条件

1) 优化目标 文中提出的考虑交通冲突类型差异的滑行路径优化模型，将一条连续的路径离散为若干个节点，每个节点表示一个滑行道交叉点，通过优化每两个节点之间的滑行路径，实现整条滑行路径的最优化.基于三类冲突下的运动学模型以及滑行延误时间计算模型，文中构建了考虑最短滑行时间T，污染物排放(z=1，2，3分别代表HC，CO和NOx)和燃油消耗F的多目标受限路由规划模型.

(20)

(21)

(22)

2) 约束条件 文中通过精细化航空器场面滑行冲突延误时间，进行路由规划.因此其约束条件结合机场场面冲突分布情况，分别对应于1.1推导出的运动约束.当遇到交叉冲突时，约束条件为1.1的式(1)～式(4)；当遇到追尾冲突时，约束条件为1.1的式(5)～式(7)；当遇到对头冲突时，约束条件为1.1的式(8)～式(11).

2 算例分析

2.1 数据获取

以上海浦东机场离港航空器从63号停机位滑行到17L号跑道起飞的滑行过程进行研究.所需的数据类型概括为以下两种：①航班数据 从上海浦东机场(ZSPD)运行指挥系统获得，包括每一个航班的航班号、机型、预计起飞落地时间、进离港时间、撤挡轮档时间等;②机场滑行路径节点信息以及机场环境信息 从中国民航航行资料汇编获得的相关机场图和机场细则，包括机场的滑行路径信息、停机位信息、机场海拔高度、温度、气压等.

2.2 考虑冲突分类的航空器场面滑行时间分析

以上海浦东机场2019年12月1日航班运行数据为例，通过统计，根据场面运行情况的繁忙程度进行划分三个时段，分别为07:00—08:00高峰时段、14:00—15:00一般时段、23:00—00:00清闲时段场面运行数据.拟合得到函数：P(h≥t)=e-λt，随飞机流服从负指数分布.其中，高峰时段、一般时段和清闲时段的λ值分别为：0.666 7、0.416 7和0.150 0.通过仿真数据分析，得到各时段航空器遇到各种冲突类型比值见表1.各时段内场面遇到各种冲突类型的次数汇总于表2.

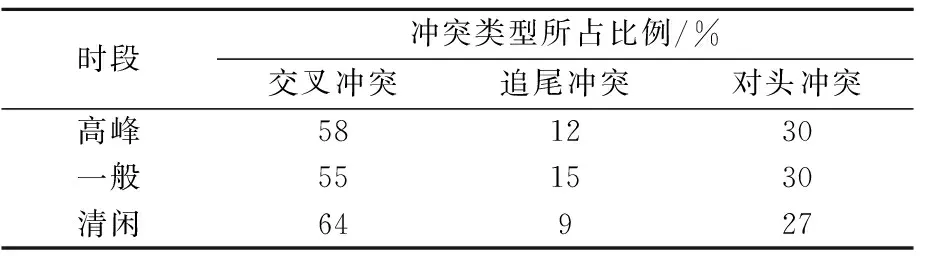
表1 各时段的各类冲突占比

结合表2中的数据选取上海浦东机场2019年12月1日三个时段内的74个离港航班作为研究对象，以航空器场面滑行实际运行数据为基础，对比分析本文采用冲突分类和文献[5]不采用冲突分类，获得的场面滑行延误时间，结果见图4.

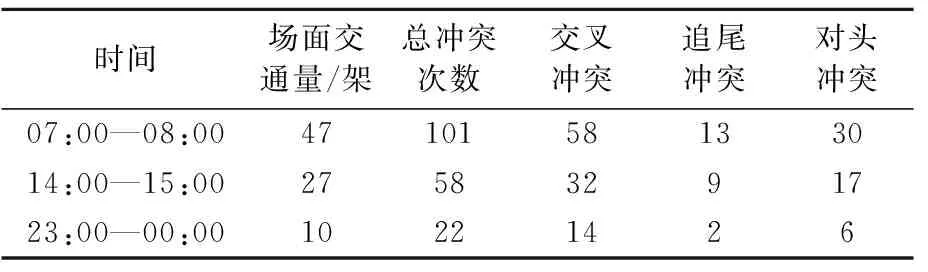
表2 各时段各种冲突类型的次数

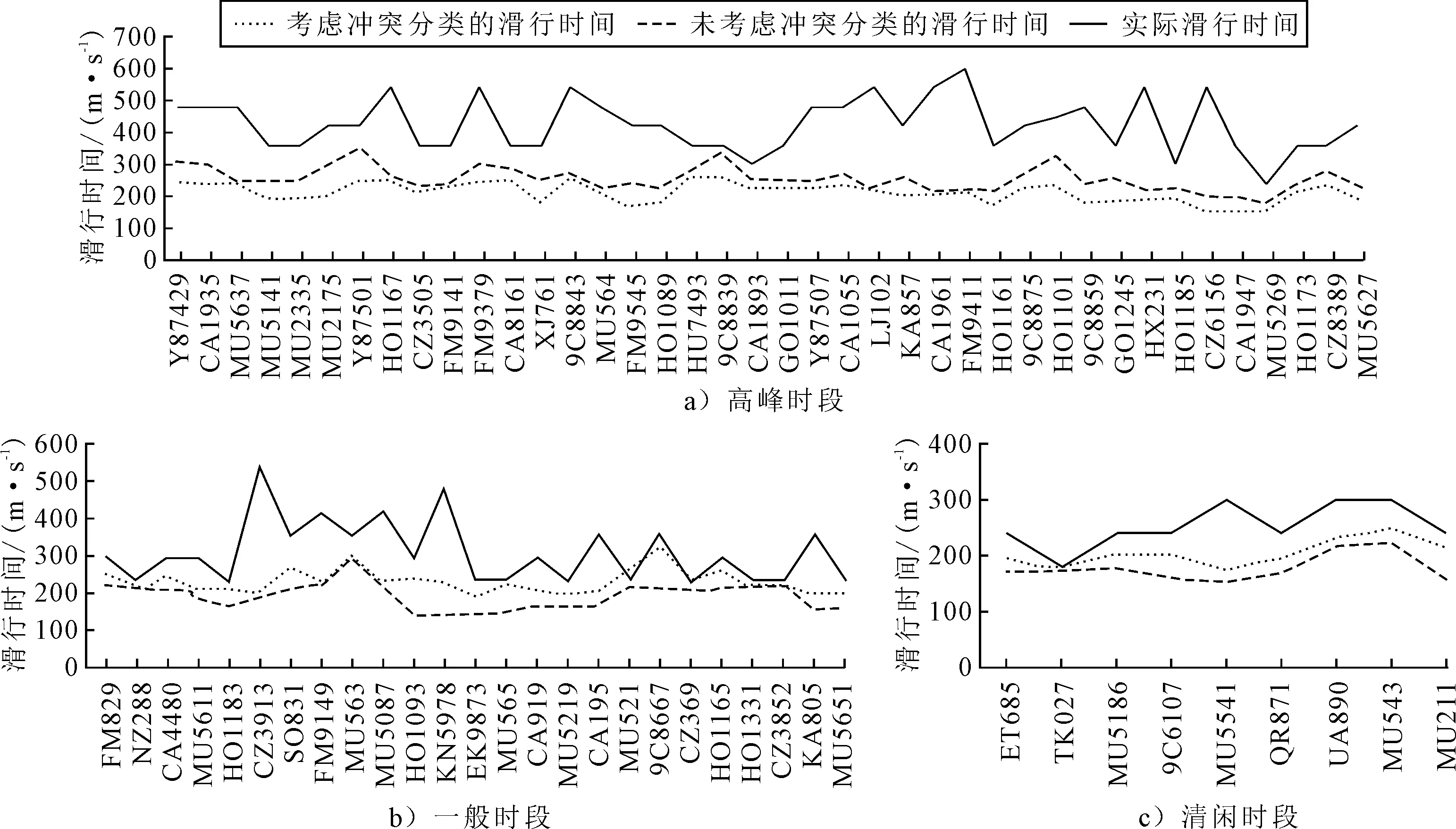
图4 各时段下滑行时间对比

由图4可知：相对于未考虑冲突分类下航班滑行时间的计算结果，考虑冲突分类下每个航班的滑行时间与该航班实际滑行时间更贴近.高峰时段，一般时段和清闲时段的准确率分别提高了9.9%，12.1%，10.3%.

2.3 航空器场面滑行路径优化结果分析

选取上海浦东机场12月1日高峰时段航班运行数据，结合上海浦东机场根据运控部门的历史统计数据定义的冲突区分布见图5，获取冲突分布以及受限路由的最短路径集.并以机型A320为例，通过NSGA-II算法进行航空器场面滑行多目标优化，得到航空器在不同滑行路径上遇到不同冲突类型下的滑行时间、燃油消耗量和污染物排放的帕累托解集.

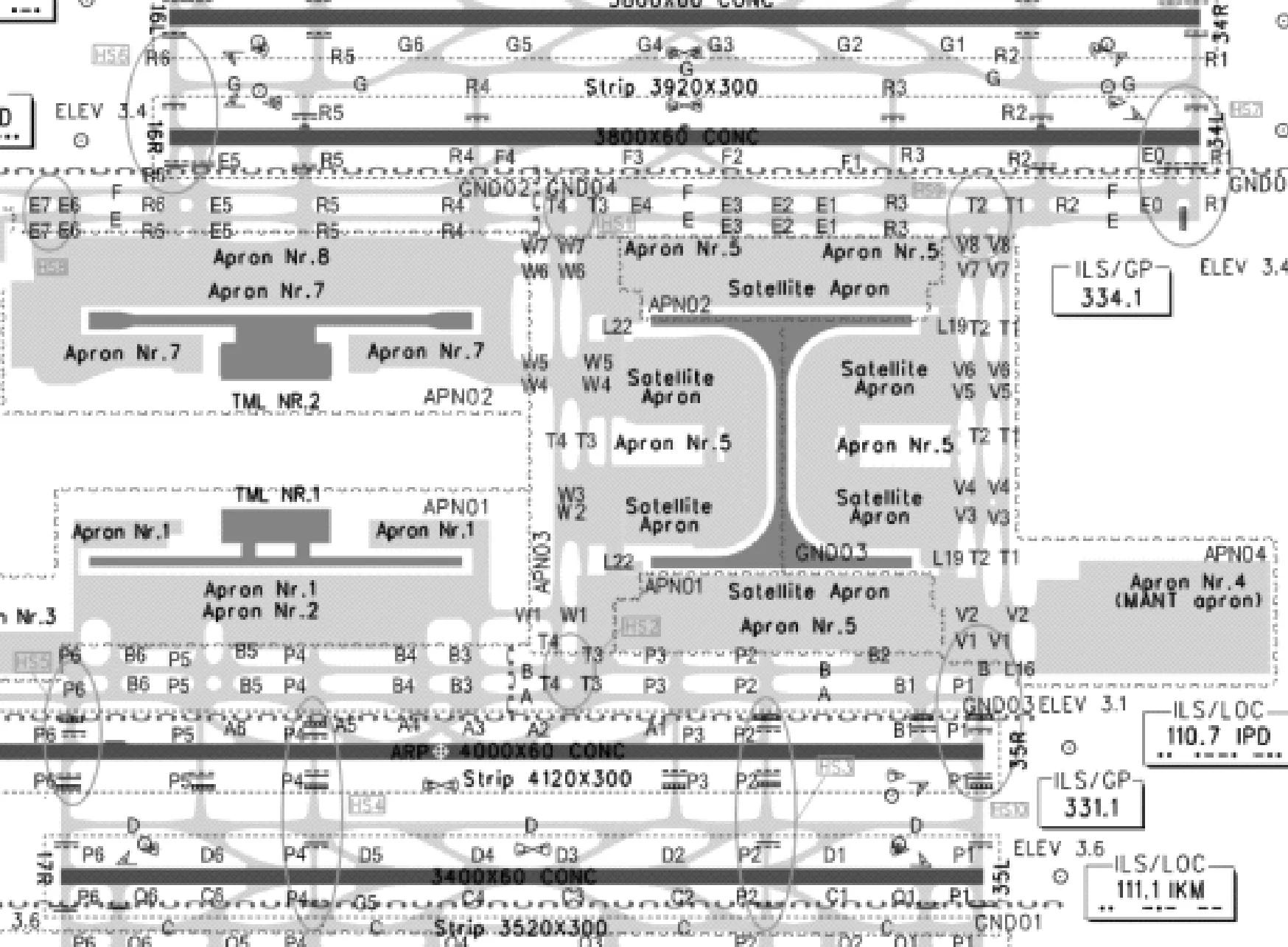
图5 上海浦东机场冲突区分布图

图5中画圈处为上海浦东机场根据运控部门的历史统计数据定义的10个冲突区，分别为HS1～HS10，在研究航空器离场滑行过程时以此为依据设置滑行过程的冲突点.结合表1～2中数据设置浦东机场高峰时段内15 min(07:45—08:00)的冲突分布，见图6.通过Yen算法进行上海浦东机场场面K最短路规划，63号停机位到17L号跑道的4条最短路径的见图7.按照距离长短排序，从最短路径到最长路径分别为路径1、路径2、路径3和路径4.

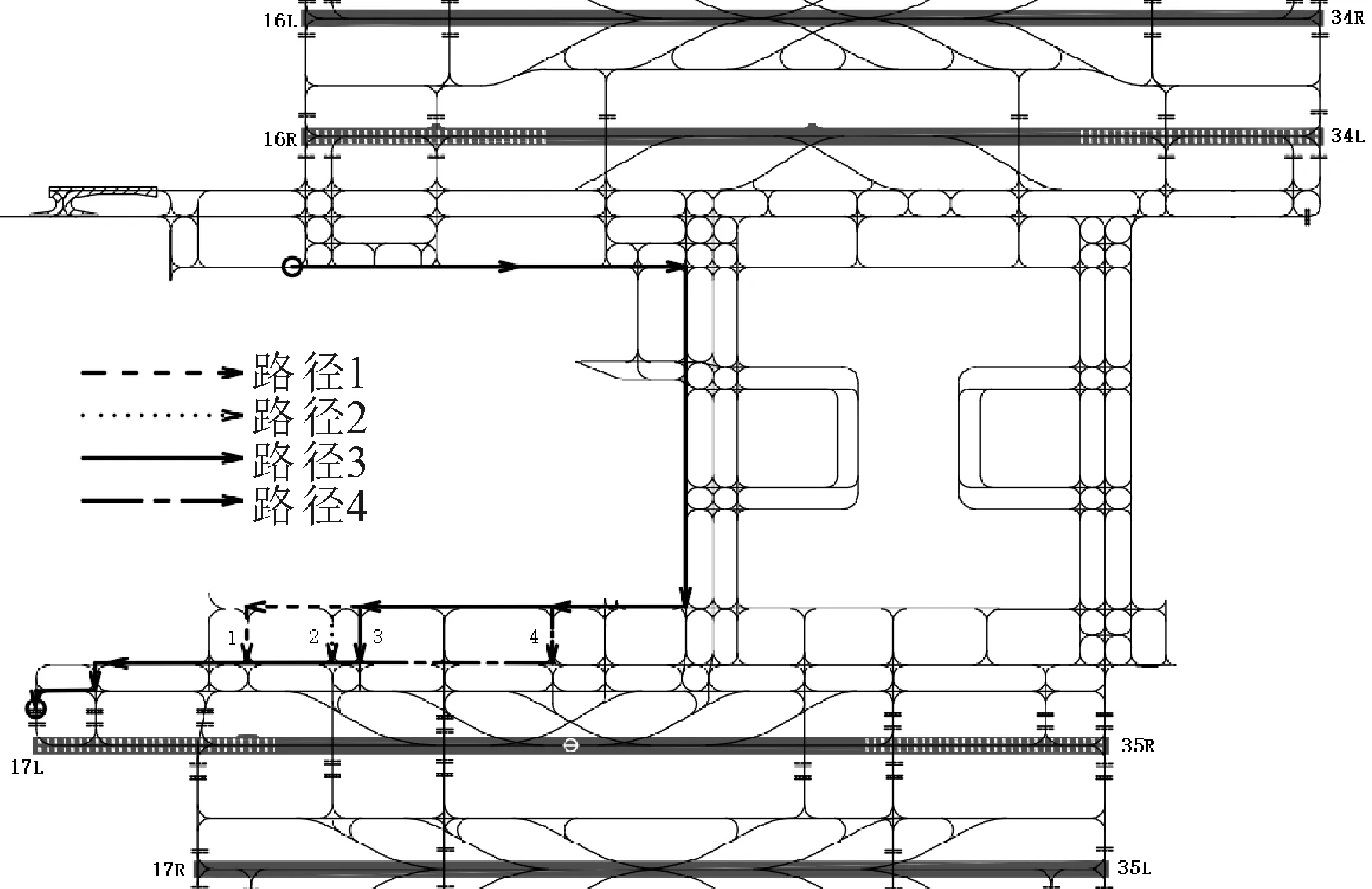
图7 最短滑行路径集

由图7可知：航空器从63号停机位滑出，终点为17L号跑道端.不同的线形分别代表优化后的四条最短路径，分别为路径1(9.906 1 km)、路径2(9.906 2 km)、路径3(9.906 1 km)和路径4(9.906 1 km).

根据图7以及2019年12月1日07:45—08:00时段进离港航班数据统计结果，以机型A320为例，通过NSGA-II算法进行航空器场面滑行多目标优化，得到航空器在不同滑行路径上遇到不同冲突类型下的滑行时间、燃油消耗量和污染物排放的帕累托解集，每条路径的帕累托最优解见表3.

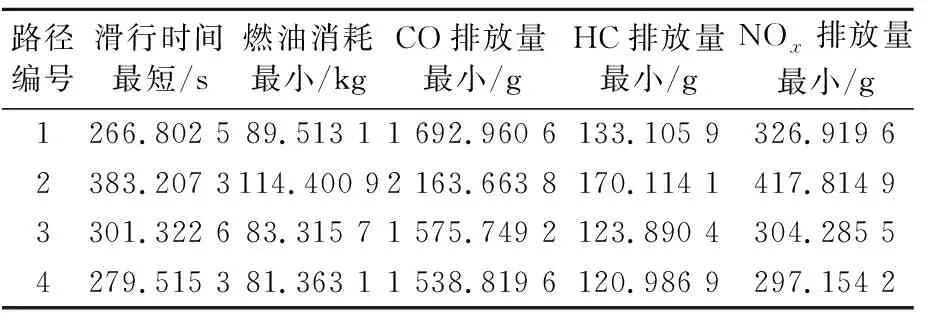
表3 各路径的多目标优化的帕累托最优结果

由表3可知：航空器在距离最短的路径1进行滑行时，其滑行时间最短，但燃油消耗量和污染物排放量均不是最小.分析可知，本实验在最短路规划基础上考虑了航空器在不同滑行路径滑行时会遇到不同冲突类型的可能性.由此可以得出，冲突类型的差异会对航空器的滑行过程产生影响.

同时，在滑行时间最短方案下，路径1为航空器的最优路径；在燃油消耗量最小方案下，路径4为最优路径；在CO、HC和NOx排放量最小方案下，路径4均为最优路径.由表3可知：燃油消耗量最小的最优路径和污染物排放量最小的路径相同，为路径4；燃油消耗量最大的路径和污染物排放量最大的路径也相同，为路径2；路径3的燃油消耗量和污染物排放量均为第二.因此可以得出航空器的燃油消耗量和污染物排放量在多目标滑行路径优化问题中呈正相关.

3 结 论

1) 各时段下航空器滑行过程遇到三种不同冲突类型所占比例及次数存在差异.各时段下，交叉冲突类型占比最高，其次是对头冲突，最后时追尾冲突，表明每种冲突类型的占比和机场繁忙程度无关.

2) 实验表明考虑冲突分类航空器滑行时间更加贴近于实际，计算结果更精确.

3) 对滑行路径最短路径集进行多目标优化结果表明，冲突类型的差异会对航空器的滑行路径产生影响，当考虑滑行冲突时，航空器的最优滑行路径由滑行距离、滑行时间、燃油消耗量和污染物排放多种因素决定.