基于改进双链量子遗传算法的有限元模型修正

陈志远 雷建平 张梓乔

(武汉理工大学交通与物流工程学院 武汉 430063)

0 引 言

有限元模型修正本质上是一个以模型计算值与实测响应值之间的误差构造目标函数，进行优化计算，找到目标函数最优解的过程．遗传算法作为一种经典的进化算法，经过多年发展，在模型修正领域得到了广泛应用．张瑞云等[1]总结遗传算法的基本原理，并运用于结构模型修正．朱宏平等[2]对基于遗传算法的模型修正方法进行改进，并运用在桥梁传感器布置方案中，证明了该方法的应用价值．秦仙蓉等[3]针对岸桥结构的有限元模型修正问题，基于Kriging替代模型及遗传算法对岸桥结构进行修正．结果表明该方法能有效修正岸桥结构参数的均值和标准差．陈义成[4]为提高发动机模型精度，建立整机稳态模型后，针对遗传算法、微分进化算法和粒子群算法三种优化算法进行了机理分析并测试比较了各个算法的修正性能，最终提出一种基于自适应变惯性权重方法的改进粒子群算法，结果表明：该方法在满足求解精度要求的同时提高了收敛性能和求解速度．康俊涛等[5]为更好控制钢桁架拱桥施工过程中标高控制可靠度，采用基于遗传算法优化的SVM模型为代理模型进行计算,并结合蒙特卡洛法求解施工期间标高控制可靠度，取得了良好的计算结果．

文中基于双链量子遗传算法，发现该算法中转角步长函数的不足，采用反正弦函数构造新的转角步长函数，并对改进后的算法进行可行性验证．改进后的双链量子遗传算法的搜索精度及鲁棒性均有提高，具有工程实际价值．

1 模型修正理论和优化算法

有限元模型修正是结构动力学中反问题的一种，参数型有限元模型的修正本质是求解多参数目标函数的最值，目标函数的构造是否合理直接影响着模型的修正效果．通常情况，目标函数都是基于理论值与实测值的相对误差来确定的，其表达式为

(1)

式中：xa为实测响应；xb为理论响应．若相对误差|Ew|小于允许误差εw，表明理论模型与实际结构相关性较好．

构造出目标函数后，有限元模型修正问题转化为求解最优的实际参数，使得目标函数|Ew|达到最小值．常用的优化算法有粒子群算法、神经网络法、遗传算法等．

1.1 遗传算法(GA)

遗传算法将目标函数的解用染色体表示，多组解即多个染色体构成一个种群，通过种群内部的遗传、交叉和变异，逐代更新染色体，当目标函数值满足精度要求或达到预设的最大代数时，结束进化，最终求得多目标函数的最优解．遗传算法流程见图1．

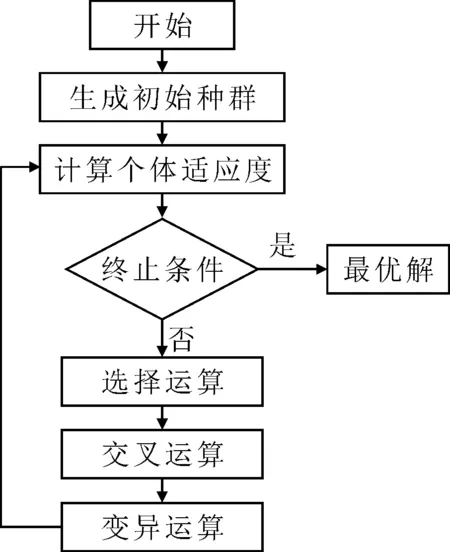
图1 遗传算法流程

在遗传算法中，n维可行解的数学形式为x=[x1,x2,…,xn]T，x为一个染色体，x中所有取值称为等位基因．根据目标函数的不同，x可以是一组整数或是某一范围内的实数，甚至可以是一些纯粹的记号．根据个体的表现型(函数值)，可由一定的规则计算出个体的适应度，适应度的计算规则与目标最优解相关，越是接近目标函数的最优点，适应度越大，反之越小．

1.2 量子遗传算法(QGA)

量子计算中，量子比特起到储存信息的作用，其本身具有|0〉、|1〉两个基本状态，每个量子位都是由这两个基态任意线性组成的叠加态，叠加态|ψ〉的形式为

(2)

式中：ci为概率幅(possibility amplitude);|ci|2的意义为量子态|φ〉坍缩到其基态|φi〉的概率．由归一化特性[6]，其表达形式为

(3)

量子态|ψ〉对应着Hilbert空间中的一个向量，基态|0〉、|1〉对应着向量空间中的一对标准正交基，其形式如下：因此，具有n个基因的染色体可用矩阵表示为

(4)

式中：|αi|2+|βi|2=1,i=1,2,…,n．

通常采用量子叠加性来产生初始种群，初始种群采用如下方式进行编码：

(5)

量子态无法进行个体适应度计算，需要先对量子个体进行测量，再将结果转化成经典信息，最终完成量子个体适应度的计算．

由量子比特Q(i)坍缩到一组确定解，确定解形式为

(6)

量子门控制量子态的旋转对应着遗传算法中的种群进化．量子态在量子门作用后发生酉变换，因此量子态的概率幅在发生变化后依旧满足归一化条件．量子旋转表达式为

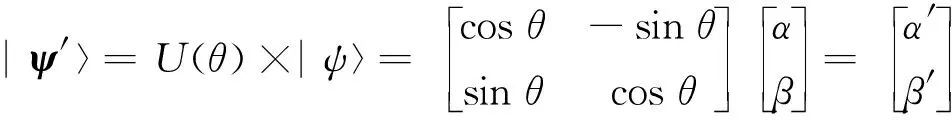
(7)

式中：|ψ〉为更新后的量子态;αi和βi为更新后量子态的概率幅．

量子旋转后，各个基态的概率幅发生了变化，种群会朝着适应度更高的方向发展，最终收敛至最优种群从而求得最优解．通常情况，量子旋转的方向与角度是根据查表确定的．

1.3 双链量子遗传算法及改进(DCQGA)

DCQGA与QGA的实现步骤基本类似，本节仅介绍二者的不同点．

在编码方式上，双链量子遗传算法中，染色体采用量子比特的两个概率幅直接进行编码：

(8)

式中：tij=2π×rand，rand为0～1之间的随机数；i=1,2,…,m；j=1,2,…,n；m为种群规模；n为量子位数．

在DCQGA中同样使用量子旋转门更新染色体，不同的是在种群旋转更新的过程中，转角Δθ是算法收敛的关键，其符号决定着种群进化的方向，其大小决定着种群更新的速度．在QGA中，转角的参数通过查表来确定，过程繁琐复杂且不能有效的利用反馈信息．为改善上述缺点，DCQGA基于梯度步长搜索理论构造转角步长函数，充分利用了目标函数变化率的反馈信息，实现了转角的动态更新，转角步长函数为

(9)

相比而言，DCQGA提出了一种基于目标函数变化率的动态更新方法，较QGA更为合理，但该函数所得的实际转角区间与较为合理的转角区间[0.005π,0.1π]相差较大，而转角过低影响算法的收敛速度，过高容易引起早熟收敛．

针对上述问题，本文尝试采用一种新的基于目标函数搜索点处变化趋势的转角步长函数，以提高算法的收敛精度．改进的转角步长函数为

(10)

改进后的函数满足转角区间[0.005π,0.1π]，更有利于种群的更新．

2 算法性能测试

为比较GA、QGA、DCQGA、改进DCQGA四者在性能上的差异，选取二维Ackley’s函数进行测试，比较四种算法的收敛精度、收敛次数及收敛用时．二维Ackley’s函数形式为

(11)

算法初始参数设置：基因位长度20，个体数量50，GA算法交叉概率0.7，变异概率0.05，最大迭代数100．每种算法各运行20次，计算结果对比见表1．

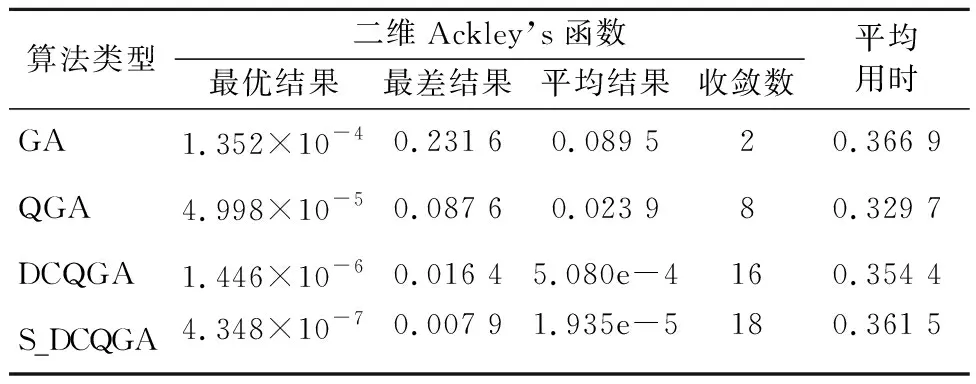
表1 算法结果对比表

由表1可知：改进转角步长函数后的双链量子遗传算法S_DCQGA是一种搜索精度高、鲁棒性强的优化算法，具有一定的实用价值．

3 数值算例验证

以计算跨径为4 m的悬臂工字钢梁为例，假定钢材因外界环境作用发生锈蚀，结构实际静动力响应与初始有限元模型计算结果相比，出现较大偏差．

假定钢板两侧锈蚀厚度相等，锈蚀后顶板、腹板、底板有效厚度分别减少了6.5，1.8和2.7 mm．选取顶板、腹板、底板的有效厚度和质量密度作为待修正参数，通过响应面法对该模型进行修正，因篇幅原因这里不再赘述．本例初始响应面函数采用二次多项式与动态权重法确定目标函数形式：

f=α1(1+Y1′/21.81)2+α2(1+Y2/22.18)2+

α3(1+Y3/28.23)2+β1(1-f1/8.059)2+

β2(1-f2/22.212)2+β3(1+f3/50.048)2

(12)

式中：f为目标函数值；αi、βi为动态权重系数．

确定目标函数形式后，采用改进双链量子遗传算法(S_DCQGA)对目标函数进行迭代求解，得到修正后的参数值，将修正后的各参数值代回有限元模型进行计算，最终得到修正后有限元模型．

修正前后参数值及相对误差见表2，静动力响应数据比较表见表3．

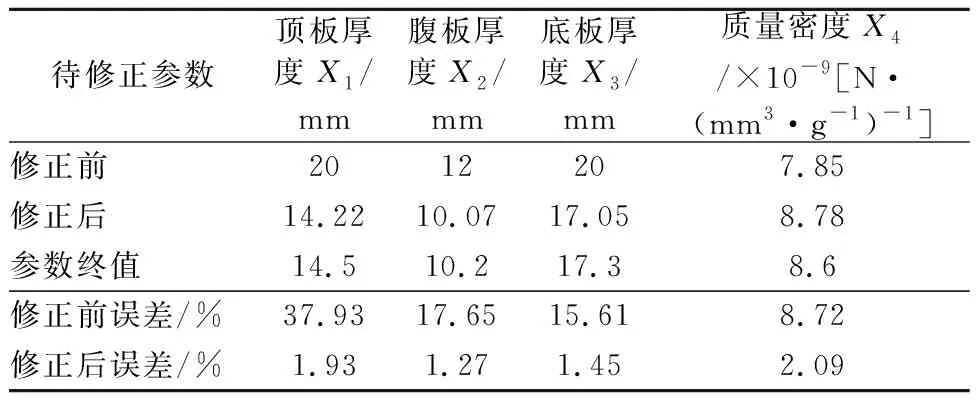
表2 参数修正前后比较表

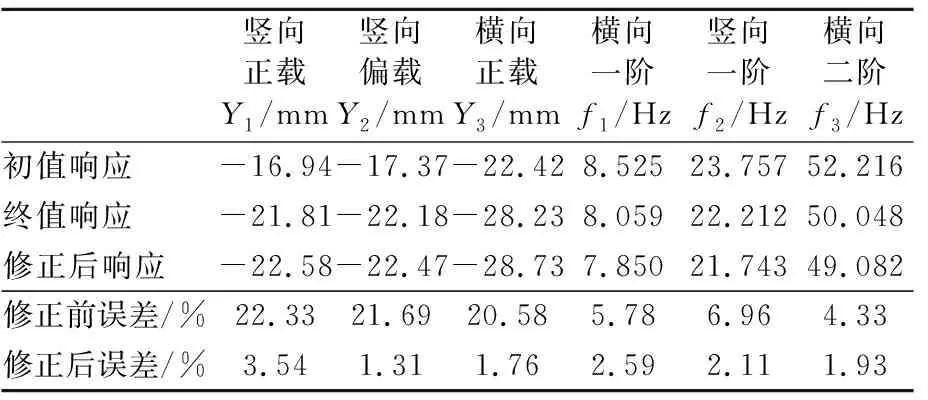
表3 参数修正前后响应比较表

由表2～3可知：几何参数修正后整体较参数终值小，质量密度修正后较参数终值大，分析认为这是由于初始有限元模型中未考虑预应力钢束的刚度、桥面铺装的刚度影响，各参数修正后误差最大为2.09%；静力响应修正后整体较终值响应大，动力响应修正后整体较终值响应小，修正效果较为明显．

为直观反应模型修正结果，静动力响应值修正前后误差见图2．各响应修正前后误差均有大幅度缩小，最低误差降至1.31%，表明基于改进双链量子遗传算法的有限元模型修正技术具有良好的实际意义和实用价值．

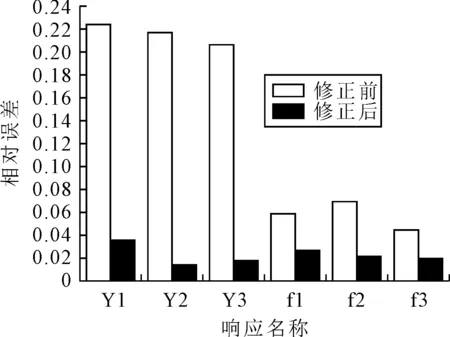
图2 静动响应修正前后误差比较图

4 结 束 语

文中基于量子遗传算法及响应面法的有限元模型修正，并改进量子遗传算法，实现了对悬臂式工字钢梁的模型修正，修正后各响应误差有明显降低、修正后参数接近参数终值，修正效果良好，并验证了采用改进DCQGA算法对参数迭代求解的可行性．

有限元模型修正的效率及准确性很大程度上取决于算法的性能，量子计算的应用目前还仅仅处于借鉴其思想的仿真阶段，远没有挖掘出其真正的潜力．后续研究将进一步开发量子计算的能力并与其它优化算法相结合，构造出性能更加优越的算法．