基于距离限制的改进Kriging模型的可靠度计算方法
2022-07-11方智勇郭细伟马亚涛骆仁杰
方智勇 郭细伟 马亚涛 骆仁杰 周 俊
(武汉理工大学船海与能源动力工程学院1) 武汉 430063) (武汉理工大学交通与物流工程学院2) 武汉 430063)
0 引 言
实际工程由于环境和施工等不确定因素,无法完全按照设计要求进行,造成结构的可靠度计算无法得出确定的结果.而且,随着结构的大型化和复杂化,传统的可靠度计算方法已经无法满足现代的可靠度计算要求.大型复杂的工程结构其功能函数大多都是非线性的和隐式的,需要借助有限元分析计算,这使得可靠度计算十分耗时,因此提出一种新的高效率、高精度的代理模型计算方法来求解结构的可靠度,从而避免对非线性的隐式功能函数求导[1].
代理模型被用来解决工程中功能函数为隐式函数和计算量大的问题,包含支撑向量机、多项式响应面法、神经网络和Kriging模型等.Kriging模型作为其中的一种代理模型,不需建立特定的多项式和数学公式,使用更为方便.
Kriging模型的精度和建立模型的样本点数目关系密切,通过增大样本点可以提高模型的精度.但对大型结构,功能函数复杂多变,增大样本点的方法使得计算量太大了,在实际工程中无法广泛运用.为解决这种弊端,将主动学习函数引入到Kriging模型建立过程中,通过主动学习函数序列选取最佳样本点并加入到初始样本点中,来更新Kriging模型.基于这种思路,提出AK-MCS和EGRA方法[2],并不断改进和研究更加高效的选点方法,如多失效模式的可靠度计算[3],引入差分进化算法[4],新IEGO学习函数[5]等.
在利用主动学习函数构建Kriging模型过程中,序列选取的最佳样本点,会因为选点策略的原因,导致新加入的最佳样本点会过于集中,陷入局部最优解.这会造成学习函数选取了大量信息冗余重复的点,计算资源被大量浪费,影响了计算效率.因此,文中在主动学习函数加点过程中引入最佳样本点之间的距离限制条件,避免了最佳样本点过分集中造成信息冗余,从而提高模型的计算效率.
1 Kriging模型
Kriging模型作为插值方法,通过未知点周围的信息来预测该点的响应值,并通过已知的统计特征来预测信息的动态和趋势,因此Kriging模型被视为最优的线性无偏估计方法[6].Kriging代理模型方法相比其他模型不需要建立一个具体的数学模型,使得这种方法的使用范围更加广泛.
Kriging模型由回归项和随机误差这两部分组成.对于个维样本点S=[x1,…,xi],其对应的响应值Y=[G(x1)…G(xi)]T,由样本和响应值之间的关系建立Kriging为
(1)
式中:回归项的fT(x)=f1(x)…fm(x)为基函数向量,主要用于功能函数的整体模拟;β=[β1,…,βm]T为回归系数向量;z(x)为随机过程误差函数,主要提供模拟的误差,其服从正态分布N(0,σ2),协方差为
Cov(z(x),z(w))=σ2R(θ,x,w)
(2)
式中:σ为随机过程的标准差;R(θ,x,w)为空间范围中任意两点x和w的空间相关函数;θ为相关参数.R函数有多种形式,其中高斯过程函数适用于非线性较强的功能函数问题.高斯方程的形式为
(3)
式中:θ为相关参数,可通过最大似然估计求得.
(4)
式中:R为相关矩阵,对于任意θ都有与之对应的一个插值模型.
对于给定的样本点,回归系数β和随机过程方差σ2的估计值由下式计算得出
(5)
(6)
式中:F为Fij=fj(xi).
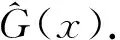
(7)
(8)

2 Monte Carlo算法计算可靠度
Monte Carlo 模拟(monte carlo simulation,MCS)又称统计实验方法,在已知功能函数的具体形式和随机变量的概率分布时,使用MCS方法计算结构的可靠度精度高,简易方便.MCS计算结果更接近真实结果,适用于并行计算,唯一的缺点是计算量太庞大[7].
MCS根据变量的统计分布类型,生成大量的符合分布的随机数,将随机数代入到函数式中,计算并分析所得到的结果.在结构可靠度计算方面,MCS方法根据随机变量的分布生成随机数,代入到功能函数Z=G(x)中进行计算.当Z<0时,记I(G(xi))=1;当Z>0时,记I(G(xi))=0.则失效概率Pf为
(9)

失效概率的变异系数为
(10)
当变异系数小于5%时,说明MCS方法生成的样本群数目足够大,满足失效概率计算的精度要求.
3 主动学习Kriging模型可靠度算法
3.1 EFF学习函数
高效全局主动(EGO )方法由于采用EI(expected improvement)函数选取最佳样本,而EI函数不是在功能函数的极限状态附近搜寻点,因此难以准确计算可靠度[8-9].Bichon等[10]基于EGO方法提出了全局可靠性分析(EGRA)方法.该方法采用EFF函数作为主动学习函数的评价指标(expected feasibility function),被用来解决工程中功能函数是非线性且为隐式的可靠度计算问题.EFF指标说明了功能函数预测值在范围的概率大小,EFF的表达式为
(11)
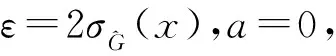
x*=arg(max(EFF(x)))
(12)
调用真实功能函数,计算最佳样本点x*所对应的响应值G*,将(x*,G*)加入到初始样本集中,重新建立Kriging模型,并计算EFF(x),直到满足条件:max(EFF(x))≤0.001,停止迭代,得到最终的模型.
3.2 基于距离限制的改进主动学习方法
MCS产生的样本群较大,样本点集中,容易出现学习函数所选取的最佳样本点聚集在一起,造成信息冗余,降低计算效率.基于此种情况,在EFF主动学习函数的基础上引入最佳样本点之间的距离限制,提出EFF(DC)(distance constraint)方法.
令x为初始样本群S中的任意一个样本点,x*为EFF函数所选取的最佳样本点,在将(x*,G*)加入到初始样本群S之前,计算x与x*之间的欧几里得距离d:
(13)
当x*与样本群S中所有的样本点距离都满足要求,即d大于某个值时,将该点加入到样本群S中,进入到下一个循环.d的距离是根据具体的函数而有所变化的,在一般正态分布随机变量中,取0.1~0.3的数值.当d小于允许的最小距离时,舍弃该点,再通过EFF函数选择另外的一个最佳样本点,计算相应的距离并进行比较,直到出现满足距离限制条件的最佳样本点.将该点加入S中,更新Kriging模型.这样的优化选点方法是避免了最佳样本点靠近已有的样本点,从而造成信息冗余,且采用EFF函数评价样本点确保了Kriging模型的模拟精度.
3.3 基于距离的EFF算法可靠度计算流程
基于主动学习Kriging模型和3.2所提出的距离限制方法—EFF(DC),结构可靠度计算流程图见图1.
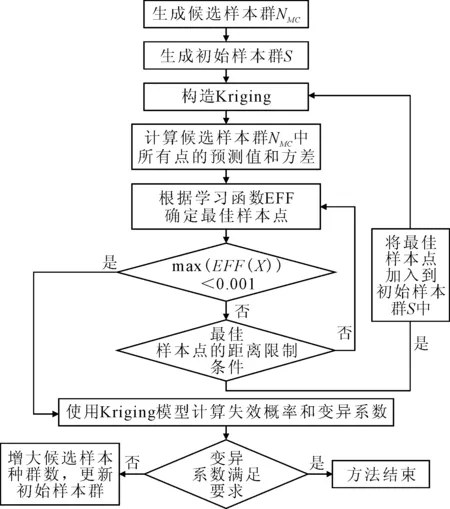
图1 计算流程图
4 算例分析
为验证EFF(DC)相比其他方法具备高效性,提出三个实际算例进行验证.将EFF(DC)和EGO、EFF、U三种主动学习函数算法的计算结果进行对比,通过结果说明EFF(DC)优化方法更加高效.将MCS方法计算所得的结果失效概率Pf作为标准解,其他方法的计算结果和标准解比较,用相对误差表征计算结果的误差大小,相对误差为
(14)
通过相对误差和调用真实函数次数来评价模型的精度和效率.
4.1 一维模型
采用文献[11]中的一个算例,其随机变量x服从N(2.5,0.52),具体的函数如下.
G(x)=1.041 7x5-13.25x4+
59.792x3-112.75x2+75.167x
(15)
为展示不同方法的计算精度和效率,选择相同的初始样本集,S=[0,1,2,2.5,5],用于MCS生成在均值±3σ附近,且数目为105的候选样本集.对于S,调用功能函数计算S中对应样本点的真实响应值,并构建Kriging模型.通过学习函数增加样本点不断更新优化Kriging模型,最后优化后的Kriging模型和优化过程中所加入的最佳样本点见图2,由此计算的可靠度结果见表1.
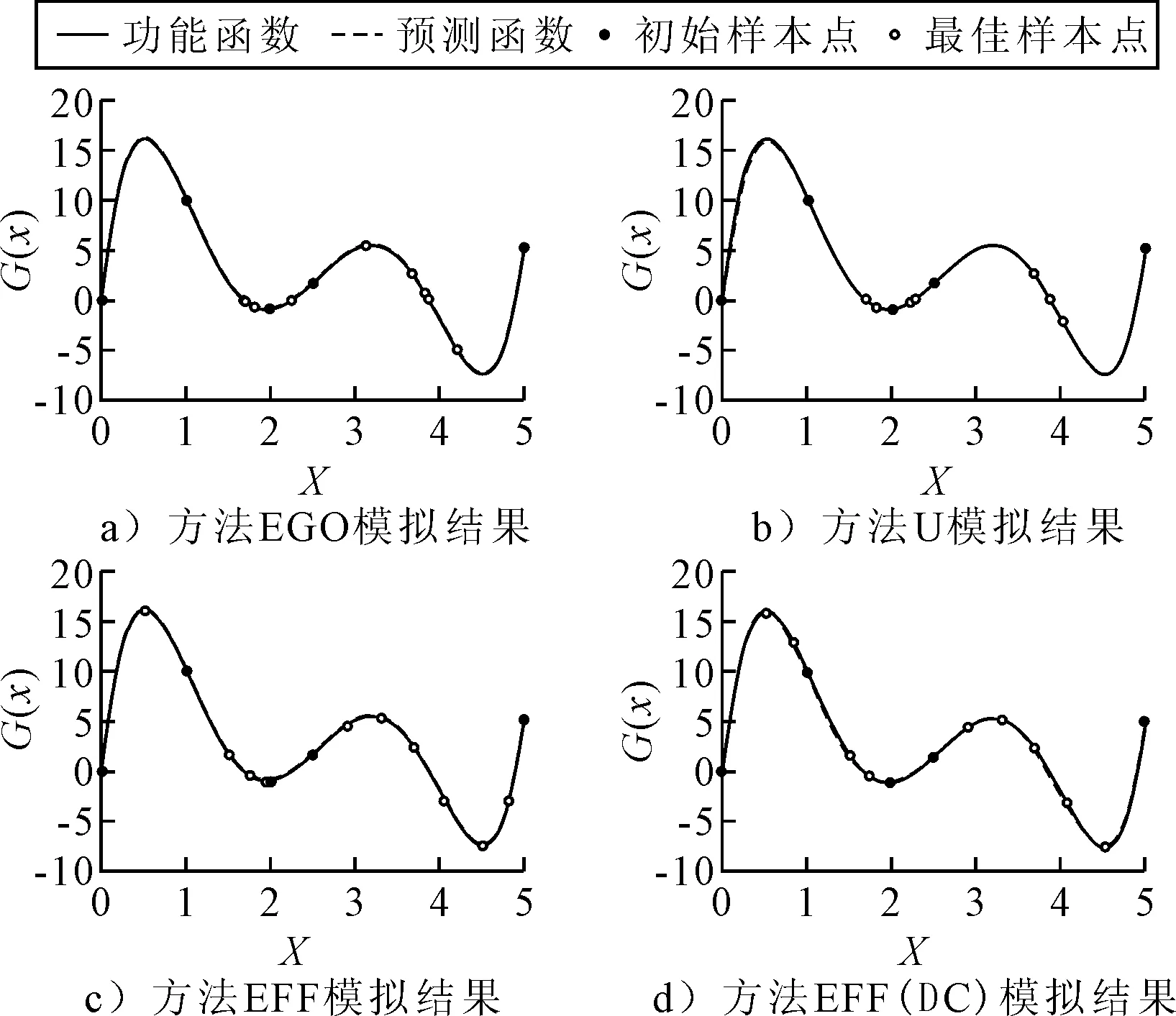
图2 算例1中不同学习方法的Kriging模型和样本点分布

表1 算例1可靠度计算结果
由图2可知:①EGO方法的选取的最佳样本点更多集中在全局最小值附近,拟合精度较好;②U方法的所选取的最佳样本点集中在1.5~2.5和3.5~4区间;③EFF方法虽然选点策略选取的是极限状态附近的点,但最佳样本点整体分布均匀;④EFF(DC)选择的最佳样本点均匀分布在整个区间,所需的样本点比EFF方法少.
用MCS方法的计算所得的结果作为标准解,四种主动学习函数的结算结果与其做对比,四种学习函数的计算所选的计算样本群数量为105.由表1可知:表1中Ncall为初始样本点数加上最佳样本点数的和.四种方法的失效概率和真实函数调用次数差距不大,EFF(DC)所需的功能函数评价次数与其他一样,但误差比其他小.
4.2 四分支串联系统问题
本算例的四分支串联系统的功能函数为
(16)
式中x1和x2为独立同分布的标准正态分布随机变量.
该算例的极限状态函数见图3.

图3 四分支串联系统极限状态函数
针对本算例,在样本空间[-3,3]上分别用四种学习函数构建Kriging模型,并计算可靠度.优化后的Kriging模型与优化过程的最佳样本点分布情况见图4.

图4 算例2中不同学习方法的Kriging模型和样本点分布
由图4可知:①EGO方法由于其本身就适用于最小值插值优化过程的选点策略,所有在本算例中表现较好,所需的最佳样本点数较少,且分布比较均匀;②EFF方法和U方法拟合程度均较好,但U方法其选点在一些区域过于集中,选点过多,EFF方法的最佳样本点数较少;③EFF(DC)的点均匀分布,不论在极限状态面附近还是内部均有最佳样本点,分布的最佳样本点不像U方法一样集中.
在算例2中,不同模型的可靠度计算结果见表2.其中EGO方法真实功能函数计算次数较少,但其失效概率的计算误差很大,结果不信;EFF和U方法的失效概率和误差相差不大,但EFF方法的真实功能函数调用次数更少.EFF(DC)仅调用真实函数52次,得到的计算结果误差为4.54%,对比于另外三种方法,既能保证计算的精度,调用的真实功能函数也较少.

表2 算例2可靠度计算结果
4.3 Rastrigin非线性函数
选择Rastrigin函数是因为其非线性程度很高,且一直作为评价全局优化算法的算例,其函数表达式为
(17)
式中,x1和x2均为独立同分布的标准正态分布随机变量.本算例中初始样本点集在附近0±3范围内获取,用拉丁超立方抽样.针对不同学习方法优化后的所得到Kriging模型和优化过程中的最佳样本点见图5.
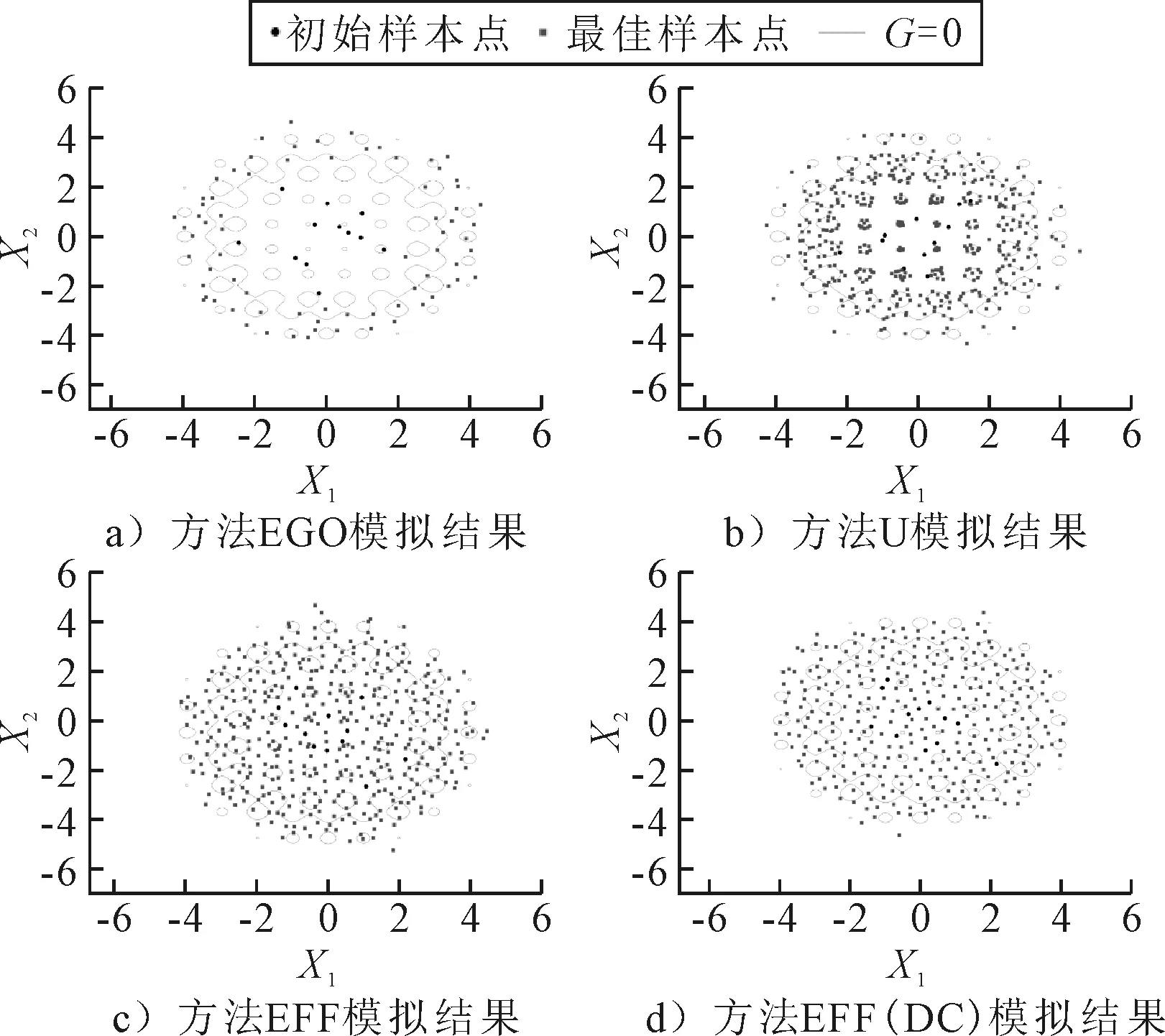
图5 算例3中不同学习方法的Kriging模型和样本点分布
由图5可知:①EGO方法所选取的的最佳样本点太少,且均集中在极限状态函数的外围,内部基本没有最佳样本点,其拟合模型的效果很差;②U方法的所选取的最佳样本点集中在G=0上;③EFF方法选取的最佳样本点在整个空间上分布均匀,拟合效果较好;④EFF(DC),选点分布均匀,但所需样本点比EFF方法点更少.
本算例的可靠度计算结果见表3,每种方法均计算50次,失效概率取这50次结果的均值,其标准差为Std,考察主动学习方法的稳定性.由表3可知:①EGO方法虽然所需要计算真实功能函数的次数最少,但失效概率为1.6%,与MCS方法的结果相差太大,相对误差为77.64%,该方法的可靠度计算的结果不可靠.②U和EFF两种方法的真实函数调用次数相近,分别是449和433次,在计算精度和稳定性上,两者也相差不大.③EFF(DC)方法,和U、EFF两种方法相比,调用的真实函数次数大大减少,只用计算335次的真实功能函数,失效概率的计算误差也较小,为0.1%.从平均值和方差看出EFF(DC)的稳定性也在可接受范围内.
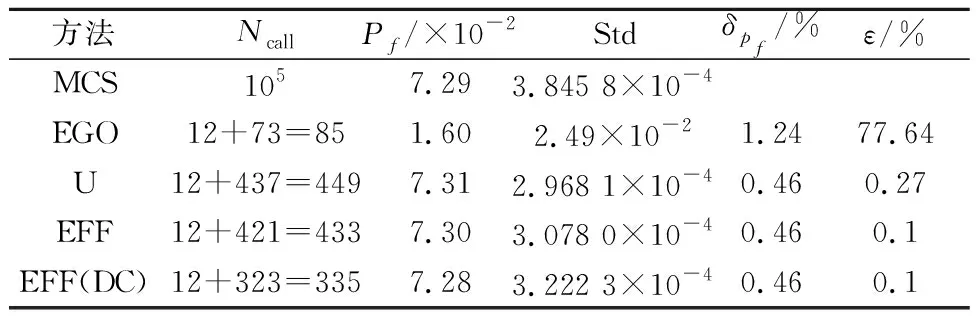
表3 算例3可靠度计算结果
5 结 论
1) 基于主动学习方法,更新优化Kriging模型.该方法充分发挥了有限的样本信息,使优化后的模型更加贴近真实的功能函数,提高了计算的精度和效率.
2) 将距离限制条件加入到主动学习函数选点过程中,减少了样本信息的重复积累,减少了有限元等数值计算的次数,提高了计算效率.通过案例的分析,EFF(DC)能够减少构建Kriging模型所需的样本点数量,有效提高计算的效率,并且能够保证计算结果的精度.
3) EFF(DC)方法并不涉及到具体的功能函数计算,因此该方法能够用于其他实际问题,具有广泛性.
