氯离子在混凝土桩基中扩散过程的有限元分析

马亚涛 郭细伟 方智勇 周 俊 骆仁杰

(武汉理工大学船海与能源动力工程学院1) 武汉 430063) (武汉理工大学交通与物流工程学院2) 武汉 430063)

0 引 言

海洋环境中自由氯离子侵入混凝土结构引起的钢筋锈蚀是降低结构耐久性的主要原因，对服役在海洋环境中的混凝土结构而言，当侵入到钢筋表面的氯离子达到临界质量分数阀值时，钢筋开始生锈腐蚀，其锈蚀产物积累产生的锈胀力致使混凝土开裂，降低结构的耐久性，缩短结构的耐久性使用寿命[1-2]．因此，为了保护钢筋不受腐蚀，需要研究氯离子在混凝土中的扩散规律，指导混凝土结构耐久性设计并预测结构耐久性．

现阶段对氯离子的扩散研究主要集中在理论分析、试验研究和数值模拟三个方面，理论分析建立在采用Fick第二定律基础上，考虑时随效应、混凝土对氯离子的结合能力和混凝土自身缺陷对扩散过程的影响[3]，并基于暴露时间和混凝土应力效应影响，建立和优化氯离子质量分数理论模型，用于混凝土结构在含氯环境下的耐久性设计和剩余寿命预测[4]．但混凝土结构的差异化使得理论研究模型并不能满足所有要求，鲁采凤等[5]利用试验研究粉煤灰掺和量对氯离子扩散的影响，发现海洋环境中的混凝土结构可以通过提高粉煤灰掺和量减弱氯离子扩散速率．Ribeiro等[6]通过改变混凝土的水灰比和水胶比、水泥类型、砂浆含量和矿物添加剂，修正了氯离子扩散系数，提高了现有模型的准确性．胡守望等[7]利用有限元软件得到氯离子扩散的数值模拟方法，利用氯离子侵蚀试验结果对扩散模拟方法进行验证，模拟分析预应力T梁内氯离子质量分数分布．Wang等[8]建立氯离子在珊瑚骨料海水混凝土中扩散模型,结合COMSOL有限元仿真软件，验证了氯离子在海水混凝土中的扩散规律与Fick第二定律一致．

由于试验周期长、理论推导的局限性,以及数值模拟参数选取的多样性等原因，对桩基内氯离子扩散缺乏研究．文中综合考虑扩散时间、环境温度和湿度对氯离子扩散的影响，对氯离子扩散系数进行耦合修正．结合修正后的扩散系数建立基于ANSYS的热分析模块的氯离子扩散模型，直观的分析混凝土内部氯离子扩散分布的规律．采用该方法分析氯离子在科特迪瓦阿比让四桥桩基中的扩散规律，预测氯离子质量分数的分布和桩基耐久性寿命．

1 氯离子扩散的有限元模拟方法

1.1 氯离子扩散方程

为准确描述混凝土内部的氯离子质量分数，Callepari等[9]在Fick第二定律基础上构建了氯离子扩散模型，描述氯离子在混凝土内部的分布，即

(1)

式中：C(x,t)为t时刻混凝土结构x深度处的氯离子质量分数值；Cs为混凝土结构表面氯离子质量分数；D0为基准时间下初始扩散系数；erf为误差函数，表述为

(2)

Fick第二定律是一个理想化的模型，假定氯离子扩散系数是一个不可变常数，其应用于一维半无限大均匀介质．但研究表明:混凝土结构中的氯离子扩散系数与混凝土结构的材料组成、颗粒级配、水灰比、孔隙率、混凝土吸附氯离子能力等内在因素有关，并与环境温度、湿度、结构所处荷载环境和结构在役时间等外部因素密切相关，故引入各种相关参数对初始氯离子扩散系数进行耦合修正，最终可以准确、高效的研究多因素影响下的氯离子扩散规律[10]．定义考虑扩散氯离子扩散时间、环境温度和环境湿度影响下的扩散系数为DM：

DM=D0·f(T)·f(t)·f(H)

(3)

式中：D0为初始氯离子扩散系数，在混凝土标准养护条件养护28 d下测得；f(T)为环境温度对扩散系数的修正系数，f(t)为扩散时间对扩散系数的修正系数；f(H)为与湿度有关的修正系数．

依据美国混凝土学会委员会有关建议，混凝土结构初始氯离子扩散系数为[11]

(4)

式中：w/c为混凝土水灰比，根据具体的工程或试验资料取值．

氯离子在混凝土中的扩散速率随温度的升高而加快，因此应考虑环境温度对氯离子扩散过程的影响，其修正系数为

(5)

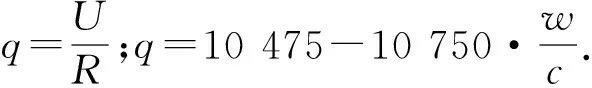
研究表明，氯离子扩散系数随着扩散时间的推移而衰减．目前公认的时间对扩散系数影响的修正系数为[12]

(6)

式中：m为与多个因素有关的时间衰减系数，由混凝土结构具体所处的环境以及相应的材料取对应的m值，见表1．

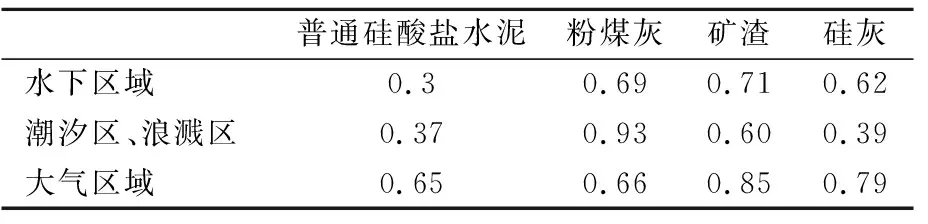
表1 m取值表

除了扩散时间和环境温度对氯离子扩散影响显著外，环境湿度对氯离子扩散也有显著影响．考虑环境湿度对扩散系数影响为

(7)

式中：HC=75%，为标准环境湿度；H为混凝土结构所处环境中的湿度值．

综上所述，氯离子在混凝土结构中的扩散方程为

(8)

式(8)中参数同上，具体取值参见试验和实际工程结构资料．

1.2 氯离子扩散有限元模型的建立

ANSYS软件中没有为研究氯离子扩散专门开发的模块，但氯离子在混凝土结构中的非稳态扩散和温度在混凝土结构中的瞬态热传导都基于扩散方程，二者从原理基础和表达形式上具有极大的相似性[13]从原理基础上讲，瞬态热传导基于能量守恒定律的热平衡方程，表达式为

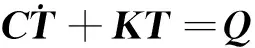
(9)

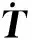
同理，由质量守恒定律可以得到氯离子的非稳态扩散用矩阵形式为

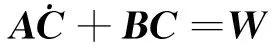
(10)

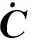
氯离子扩散方程和热传导方程为

(11)

(12)

式中：ρ为混凝土密度；c为混凝土比热容；Dx为氯离子x方向的扩散系数；Dy为y方向的扩散系数(以二维为例)；γx,γy分别为温度沿x、y方向的导热系数．综上所述，采用ANSYS软件内的瞬态热传导模块，通过等价的参数替换，可以对氯离子在混凝土结构中的非稳态扩散规律进行相应的模拟分析，对混凝土桩基结构内氯离子扩散过咸亨进行研究．

2 模型验证

根据文献[14]中试验，采用普通硅酸盐水泥制成的100 mm×100 mm×400 mm混凝土小梁，设计混凝土强度为C30，设计水灰比为0.49；试块成型后在标准养护条件下养护28 d，然后进行试验．采用环氧树脂封闭混凝土小梁侧面后放入温度为30 ℃、质量分数为15%的氯化钠溶液中进行侵蚀试验，浸泡总时长为60 d，分别对侵泡30、45、60 d试件进行取样，每次取样深度为5 mm，借助RCT试验快速测定混凝土中自由氯离子的含量，测得混凝土小梁试件在各周期内不同深度处自由氯离子含量见表2．

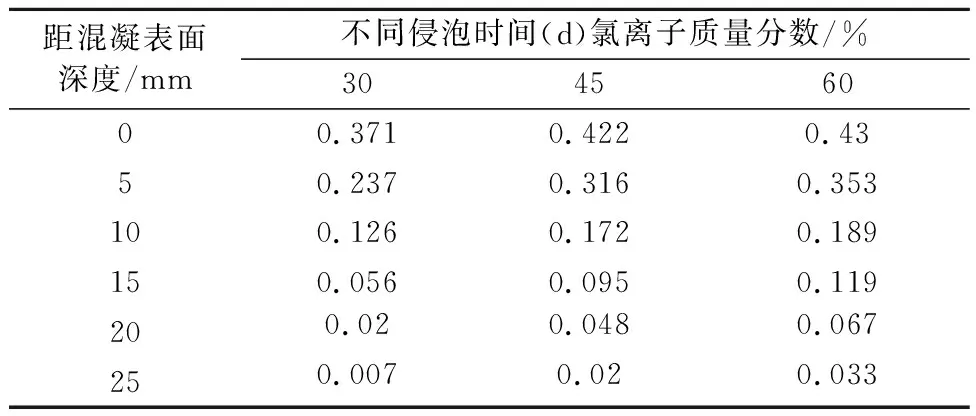
表2 氯离子扩散质量分数试验值

2.1 模型建立

以混凝土小梁的单一截面为研究对象，建立100×100 mm的正方形模型，固定网格尺寸为2 mm对截面模型进行网格划分，网格图见图1．

图1 有限元模型及网格划分

定义瞬态热传导分析、设置初始氯离子质量分数值施加荷载，设置荷载步和步长，通过求解模块控制输出、求解,以及后处理，实现对氯离子扩散的模拟．具体参数见表3．

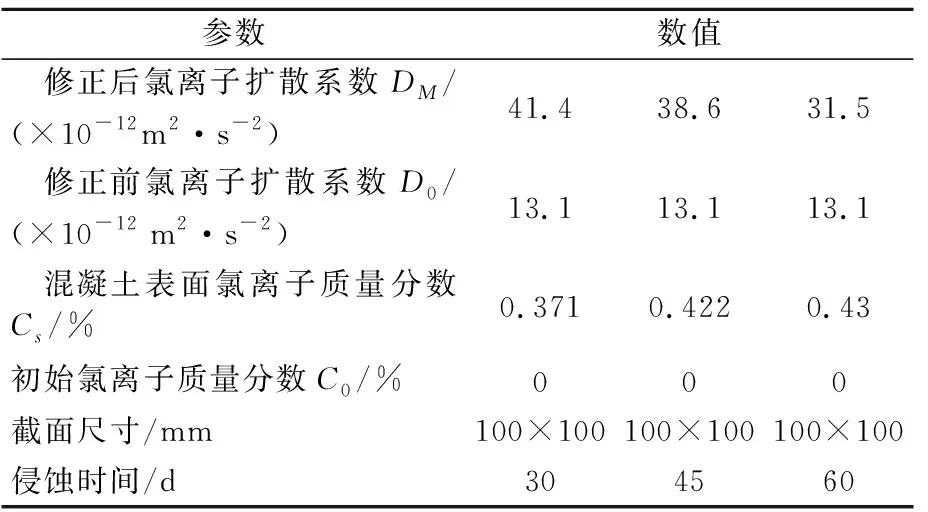
表3 模型参数

2.2 结果分析

选择ANSYS瞬态热传导分析模式，分别对扩散系数修正前后的模型进行计算，扩散时间分别定义为30、45和60 d.计算结果可知：混凝土梁截面内氯离子质量分数模拟值随着扩散深度的增加而减小，且同一扩散时间，相同的扩散深度，采用修正后的扩散系数得到的氯离子模拟质量分数值较扩散系数修正前的模拟质量分数值大．氯离子扩散质量分数试验值与模拟值对比见图2.

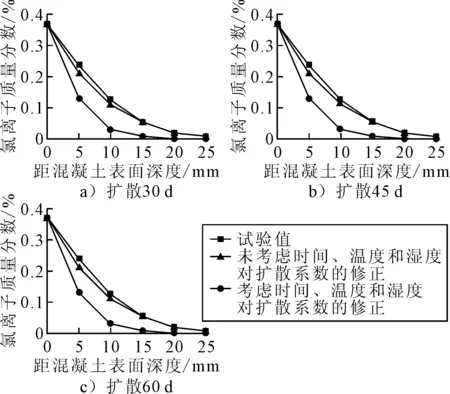
图2 氯离子扩散质量分数试验值与模拟值对比

由图2可知：ANSYS有限元方法对氯离子扩散进行模拟得到的质量分数分布结果与试验结果整体变化规律相同，氯离子质量分数值随氯离子扩散深度的增加而减小．采用修正前的扩散系数模拟得到的氯离子质量分数比相同位置的试验值小，同样也比采用修正后的扩散系数模拟得到的结果小，说明在扩散时间、环境温度，以及湿度的耦合影响下，氯离子在混凝土中的扩散速率明显增大．选用修正后的扩散系数模拟得到的氯离子质量分数分布结果与试验值整体具有较好的拟合性．但在侵蚀表面0～5 mm，二者拟合性较差，模拟值和试验值最大的误差分别为11%(30 d)、17%(45 d)和20%(60 d)，均超过10%．这是由于表层区域运输机理的复杂性导致距离混凝土表面小范围内模拟值与试验值出现了较大误差．超出该表层区域外的其他位置，氯离子扩散质量分数的模拟值和试验值最大误差分别为5%(30 d)、7.3%(45 d)和5.9%(60 d)，满足误差精度要求．因此，该方法可以较为准确模拟氯离子在混凝土中的扩散过程，预测氯盐环境中混凝土结构内氯离子质量分数分布和实际混凝土结构的耐久性寿命．

3 工程实例

3.1 建模与分析

该桥桩基为钢筋混凝土结构，桩基半径为1.05 m，钢筋直径为25 mm，保护层厚度为100 mm，混凝土密度为2 500 kg/m3，水灰比为0.45，所处地理位置气温平均25 ℃．由于混凝土桩基结构沿高度方向混凝土材料参数、表面氯离子质量分数均相同，所以可以认为桩基的水平截面都是相同的，因此基于二维分析模型建立氯离子在桩基内部扩散的有限元分析模型，具体参数见表4．

表4 模型参数取值

桩基水平截面为中心对称结构，采用1/4模型模拟氯离子在桩基内扩散，见图3a)．设定氯离子侵蚀为100年，设置输出控制，后处理输出氯离子分布云图见图3b)．由图3b)可知：该桥梁桩基结构的氯离子质量分数分布规律为桩基表面质量分数最大，桩基中心位置质量分数最小，质量分数值随着扩散深度的增加而减小．

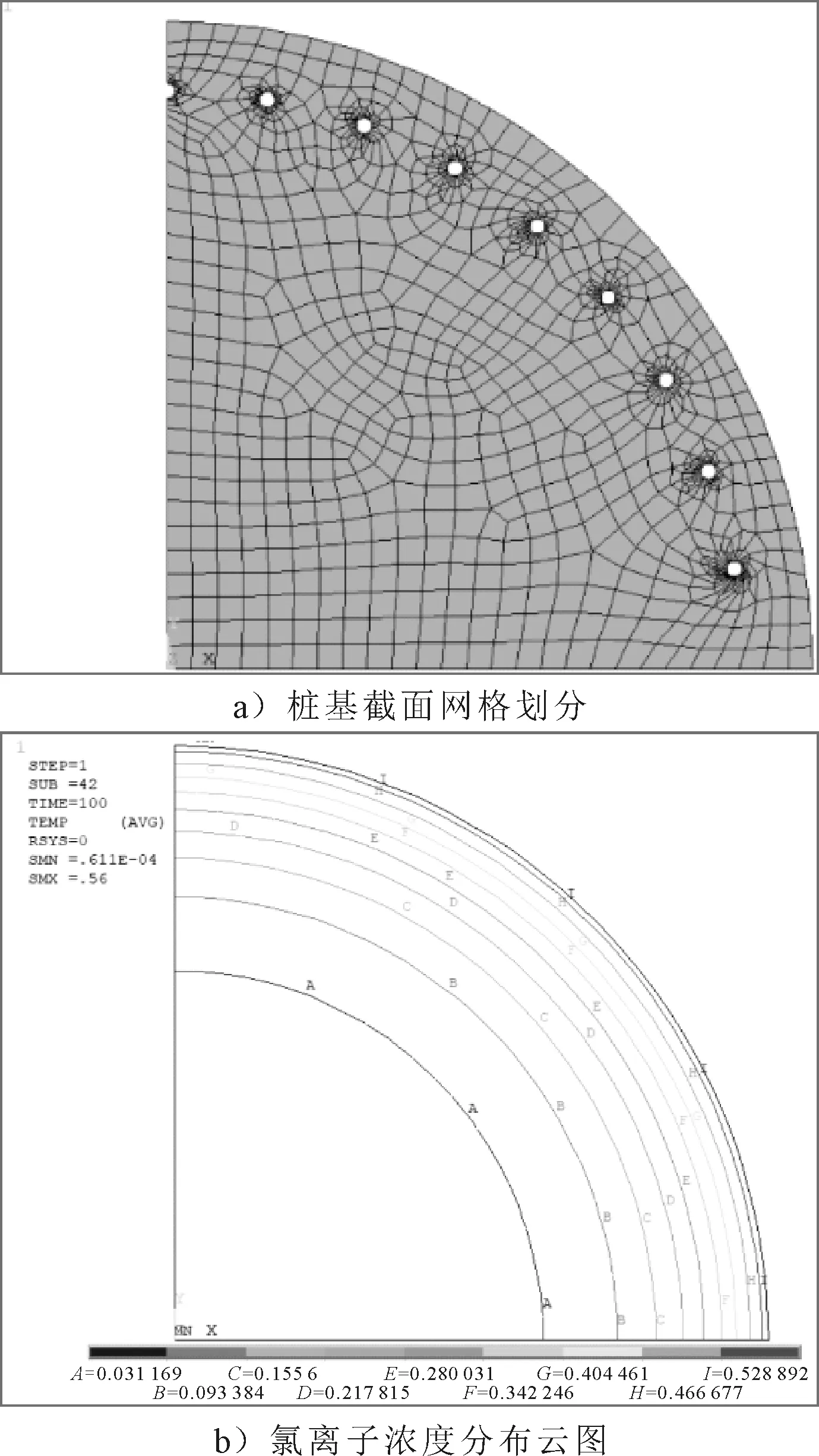
图3 桩基结构有限元模型

图4为氯离子质量分数分布等值线图．由图4可知：两种情况下都符合氯离子在混凝土内部的扩散分布规律，但二者存在差异：考虑钢筋存在时，桩基内部钢筋位置周围的自由氯离子质量分数值高于相同位置没有钢筋时的氯离子质量分数值，具体表现为图4a)中氯离子质量分数等值线D、F在钢筋位置处凸向钢筋．

图4 氯离子质量分数分布等值线图

图5为桩基内氯离子质量分数变化图．由图5a)可知：考虑钢筋存在时，保护层厚度处的氯离子质量分数值明显高于同等条件下不考虑钢筋不存在时的氯离子质量分数值，且二者质量分数差值值随着扩散深度的增加而变大，在钢筋表面位置最大的差值为19.8%．这说明桩基内部钢筋对于氯离子扩散有较大的阻碍作用．由图5b)可知：两者氯离子质量分数比值随着扩散深度的增加先增大再减小，在保护层厚度位置处，考虑钢筋存在的氯离子质量分数预测值是不考钢筋时是的1.2倍．因此，利用该有限元方法预测桩基内部氯离子质量分数分布时，钢筋的存在致使钢筋表面氯离子质量分数达到质量分数阀值的时间缩短，从而影响桩基的耐久性，导致耐久性寿命缩短.

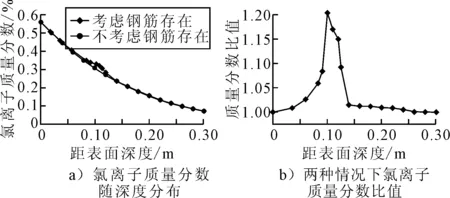
图5 桩基内氯离子质量分数变化图

图6为钢筋表面位置处氯离子质量分数随侵蚀时间变化曲线．由图6可知：同一时刻，考虑钢筋存在情况下，处于保护层位置的氯离子质量分数值明显高于不考虑钢筋时相同位置的氯离子质量分数值，且两者之间质量分数差随着氯离子侵蚀时间而增加．

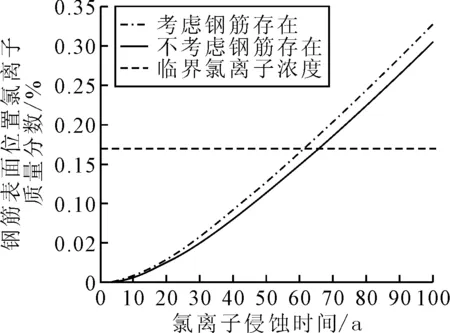
图6 钢筋表面位置处氯离子质量分数随侵蚀时间变化曲线

3.2 桩基耐久性寿命计算

结合本文方法，通过模拟氯离子在混凝土结构的扩散过程，得到钢筋表面位置任意时刻的氯离子质量分数，从而预测桩基耐久性寿命．现有的研究表明，耐久性寿命[15]分为2个阶段．

第一阶段为氯离子从混凝土表面向内部渗透，到钢筋开始锈蚀所需要的时间，这个时间为初锈时间．因此，设定钢筋表面临界质量分数为0.17%，由图6b)可知，考虑桩基内钢筋存在时，桩基的初锈时间61.5年，不考虑桩基内钢筋存在时，通过该方法模拟得到桩基的初锈时间为65.8年，比考虑钢筋存在情况下初锈时间增加7.0%．

第二阶段为钢筋开始发生锈蚀到混凝土结构保护层开裂至极限值所需要的时间t，为

(13)

ΔD=2×r·(1-

(14)

式中：ΔD为截面直径损失；icorr为单位锈蚀电流密度，icorr=1 μA/cm2；αE为钢筋锈蚀产物的膨胀率，一般选为2.18；Δw为桩基混凝土保护层裂缝宽度；Δrs为钢筋半径损失量；C为保护层厚度；r为钢筋半径．将该工程具体参数代入式(13)～(14)中，求得第二阶段时间t=24年．综上可得，考虑钢筋存在对氯离子扩散的影响，科特迪瓦桥梁桩基耐久性寿命为85.5年，不考虑钢筋存在对氯离子扩散的影响下，科特迪瓦桥梁桩基耐久性寿命为89.8年．

4 结 论

1) 通过分析对比氯离子非稳态扩散和ANSYS瞬态热传导的规律，建立氯离子在混凝土中的有限元扩散模型，将有限元模拟结果与试验值就行对比，验证该方法的有效性．

2) 考虑扩散时间、环境温度和湿度对氯离子扩散系数的修正，发现采用修正后的参数对氯离子扩散过程模拟的精度高于未修正参数下的模拟结果，更好的适用于桥梁桩基氯离子扩散．

3) 基于文中验证的有限元模拟方法，对科特迪瓦桥阿比让四桥桩基进行模拟，发现桩基内钢筋表面存在氯离子聚集的情况，并且考虑钢筋存在得到的初锈时间比未考虑钢筋得到的初锈时间短，分别为85.5年和89.8年，缩短了4.8%．因此，考虑对桩基内钢筋表面进行防锈处理，提高钢筋生锈的氯离子质量分数阀值，延长桥梁桩基结构的耐久性寿命．