基于Geohash编码的共享单车分层调度方法研究

李 福 徐良杰 罗剑萍* 朱然博 刘 静

(武汉理工大学交通与物流工程学院1) 武汉 430063) (湖北文理学院汽车与交通工程学院2) 襄阳 441053)

0 引 言

共享单车解决了公共交通难以实现“最后一公里”末端需求的弊端，近年来受到公众的青睐得以快速发展．相比有桩停放的公共自行车，共享单车的借还车不受场地限制，完全由用户的出行行为驱动．另一方面，由于不同区域的用地性质的不同而产生的出行吸引量与发生量的差异，造成了共享单车的空间分布不均．制定科学合理的调度策略有助于解决共享单车的供需失衡问题，提高共享单车的资源利用效率．

共享单车与公共自行车的调度问题均可转化成车辆路径问题(vehicle routing problem, VRP)．在调度方法上，主要为传统的库存-路径模型，即一个调度站服务若干租赁点，在各个租赁点间寻找最优调度路线．Bell等[1-2]均以运营商的总调度成本为目标对调度路径进行寻优；Liu等[3-4]以出行者的广义出行成本为目标；Liang等[5]以提高用户的满意度为目标；Gao等[6-7]以总调度距离最小为目标；于德新等[8]以成本最小和投放率最高为目标进行多目标优化；Yang等[9]以成本最小和运转量最大为目标；李兴华等[10]以用户需求的损失最小、用户出行时间最短为目标，建立双层规划模型．

在实际的调度作业中，由于单个调度站的服务范围的限制，经常会划分不同的调度区分别进行调度作业，从而提出分层调度策略．徐建闽等[11]根据公共自行车的时空分布特性，将距离较近且调度需求的时空分布类型相似的站点设为同一层；关宏志等[12]将调度车分为两类，采用大型调度车收集调度需求密集站点，采用小型车收集小区内分散站点，进行上下两层调度．由于分层调度方法过于主观化，分区依据不明确，实际应用时难以实施．

传统的调度方法将调度站所服务的区域内的整体供需视为平衡状态，只考虑区域内的调度路径，忽略了各区域间的车辆流通．当前共享单车调度问题的研究大多集中于数学建模的过程，忽略了基于实际数据进行调度需求分析．本文基于北京市摩拜单车的用户骑行订单数据，分析不同区域范围下的共享单车的调度需求，采用Geohash地理编码划分不同层级的调度站的服务范围，进行分层调度．

1 调度需求与调度方法分析

1.1 调度需求分析

共享单车的运营时空数据可较好地反映用户的骑行时空特征[13]，从而挖掘出共享单车的借还车需求量与调度需求量的空间分布．选用北京市的摩拜单车的用户骑行历史订单数据，分析共享单车的调度需求．原始数据集包含共享单车用户的订单号、共享单车ID、用户ID、单车类型、骑行的起始时间、骑行的起点和终点位置．数据样本集涵盖了两周的3 214 096份摩拜单车用户出行订单，包含485 465辆共享单车和349 693个用户．

对骑行的起终点位置采用Geohash地理编码进行网格划分．其原理为通过二进制将一定经纬度范围的区域进行分割，把二维的空间经纬度数据编码成字符串，该区域内的点共享一个编码．Geohash编码的位数越多，则区域分割的次数越多，区域面积越小．不同位数的Geohash编码对应的区域范围见表1．

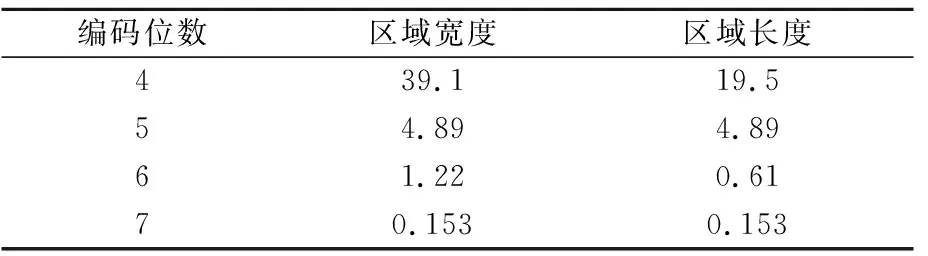
表1 不同编码位数的区域范围 单位：km

利用Python中的pandas工具包对原始数据集进行处理，删除异常数据后，以1 h为时间间隔，累计各个编码区域内的用户的借车量与还车量．当某区域一段时间的用户借车量与还车量之间存在差值时，则该区域存在着调度需求．分别以编码位数为4、5、6、7对北京市进行区域划分，统计不同编码位数区域内的累计借还车差值(绝对值)分布，见表2．

表2 不同编码位数区域内的调度需求分布 单位：辆

由表2可知:以编码位数为4、5、6、7对北京市进行区域划分时，每块区域内的平均调度需求分别为235、57、21、3．随着划分区域的增大，区域内的调度需求增加，但单位面积内的调度需求大大减少，即区域内的共享单车的借车与还车需求相对更加平衡．

1.2 分层调度方法

传统的调度方法为一个调度站服务一定的区域范围，通过调度车将共享单车从一处供大于求的租赁点搬运至另一处供小于求的租赁点．传统的调度方法仅依赖区域内的调度无法实现该区域的供需平衡，调度站需容纳一定量的共享单车以供调度，蒋塬锐等[14]基于该问题提出了基于调度池的调度方案，但该方案未考虑调度站的容量限制，调度站存放的共享单车同样需调入或调出．

为此，提出一种新的适用于共享单车的分层调度方案，上层调度区:39.1 km×19.5 km,中层调度区:4.89 km×4.89 km,底层调度区:1.22 km×0.61 km,见图1．

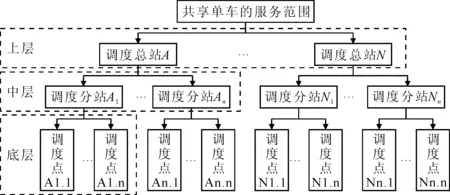
图1 分层调度方案示意图

2 区间调度模型

2.1 VRP理论

在VRP理论基础上考虑共享单车调度服务特性，某一区域内的共享单车的调度过程见图2．

图2 共享单车区间调度示意图

2.2 模型假设

考虑到实际调度场景的复杂性，为了使调度问题抽象为数学模型且较为真实的反映图4中的区间调度场景，对模型做出如下假设.

1) 任意两个调度点间均有道路连通．

2) 所有调度车均从调度站出发且最终返回调度站，为简化模型，一辆调度车只对每个调度点最多访问一次．

3) 调度站与调度点有足够多的空间可容纳一个周期内所需调入或调出的共享单车．

4) 以一定时间段为调度周期，所有调度任务均可在调度周期内完成．

2.3 模型建立

对于某层级的调度区，存在一个调度站点集合V={V0,V1,…,Vn}，其中V0为调度站，Vn为其负责的n个调度点．调度站点与站点间的道路构成网络G，G=(V,A)，其中A为调度点间的道路的集合，A={(i,j);i,j∈V,i≠j}，调度点Vi和Vj间的最短运输距离为lij．调度站内的调度车用集合K表示，K={K1,K2,…,Kn}，每辆调度车的最大可装载q辆共享单车．

以时间T为调度周期，调度点Vn在调度周期内的调度需求为dVn，当dVn<0时，表示调度点的共享单车为过饱和状态，需调出|dVn|辆共享单车；当dVn>0时，则需调入dVn辆共享单车．在分层调度方案中，调度总站与调度分站的调度需求取决于底层调度区的调度点的调度需求，对于调度点Vn，以时间T为调度周期时，其调度需求的计算方法为

(1)

式中：drent(t)、dreturn(t)分别为调度点Vn所在区域在时刻t的用户借车量与还车量．

对于共享单车运营企业，其在执行调度方案时首要考虑的为调度成本，包括调度车的运行成本和调度员的作业成本两部分．计算方法为

(2)

(3)

式中：Cveh、Clab分别为调度车的运营成本和工人的作业成本；ck、cf分别为调度车的折旧成本和每公里的油耗成本；ct、cv分别为调度员的单位时间薪资和每辆共享单车的作业薪资；v为调度车的平均行驶车速；drVn为调度点Vn在调度作业时的实际调入或调出车辆数；x(ij,Kn)为二元变量，其值为1时表示调度车Kn经过调度点Vi和Vj，反之x(ij,Kn)=0．

由式(2)～(3)可知:调度车的运营成本和工人的作业成本均与调度量呈正相关，即调度量越小，调度成本越低．考虑到实际调度量的下限值无法进行有效约束，为保证调度方案的正常执行，设定当某个调度点的调度需求未被满足时，存在着惩罚成本．惩罚成本定义为：对于共享单车系统，当借车需求未满足或车辆闲置产生的收益下降与资源闲置浪费成本，具体量化方式为

(4)

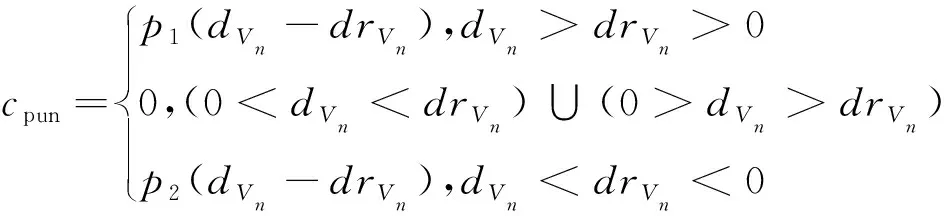
(5)

式中：p1、p2分别为借车需求未被满足和车辆闲置时，每辆共享单车的惩罚成本．

在上述模型假设的基础上，以广义的调度成本最小为目标，建立模型.

minC=Cveh+Clab+Cpun

(6)

s.t.

(7)

(8)

(9)

(10)

∀Kn∈K,∀Vn∈V

(11)

∀Kn∈K,∀Vn∈V

(12)

x(ij,Kn)∈{0,1},∀Kn∈K,(i,j)∈V

(13)

式中：q(Kn,0)为调度车Kn离开调度站时的初始装载量；x(ij,Kn)为二元变量．

约束条件(7)～(10)针对模型的假设2，式(7)～(8)为每个调度点最多被服务一次(允许不被服务)；式(9)为当调度车不经过站点Vn时，其调入或调出的车辆数为0；式(10)为调度车的起终点为调度站；式(11)为调度车在任意调度点作业时，其装载的共享单车数量满足最大装载量的约束；式(12)为调度车在任意调度点作业时，其可卸载的共享单车数量满足其当前装载量的约束．

3 案例分析

以北京市内Geohash编码为wx4eh的区域为中层调度区，采用6位编码将该区域划分为32个底层调度区，见图3a)．采用均值漂移算法对骑行起讫点进行聚类处理，确定各底层调度区的用户骑行聚集位置，即为调度点，见图3b)．

图3 调度图

随后确定调度方案的执行周期．图4为Geohash编码为wx4eh在5月10—16日一周内的每小时的借车与还车量的差值的变化过程．由图4可知:当调度方案的执行周期小于24 h时，需在1 d内多次执行调度；调度周期过长则会造成每个周期的调度任务量多大，调度站难以容纳过多的共享单车，因此选取24 h为调度周期较为合适．

图4 一周内的共享单车借车与还车量变化

在此调度周期下，以5月10日为例，根据骑行的历史订单数据，各调度点的调度需求见表3．在实际进行调度作业时，由于共享单车需求量的可预测性，可采用机器学习等方法对调度需求进行预测，以此为依据制定调度方案．

表3 各调度点的调度需求 单位：辆

假定调度站V0位于区域wx4ehk内，根据各调度点的具体位置和路网分布，距离矩阵见表4．

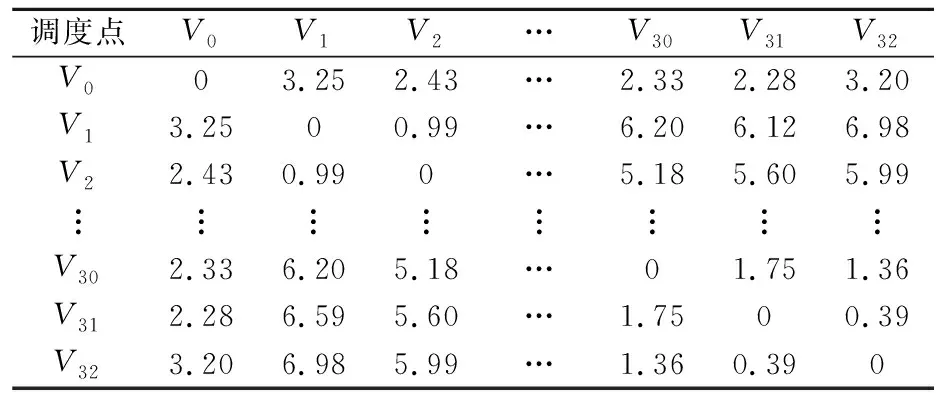
表4 距离矩阵 单位：km

设置区间调度模型的相关参数：设调度车的最大可装载量90辆，平均行驶速度为30 km/h，油耗成本为0.72元/km，每个周期内的折旧成本为13元．假定惩罚成本中，p1、p2分别为1.5、-1.0元/辆．根据调度员的行业薪资水平，确定调度员的单位时间薪资和每辆共享单车的作业薪资，对区间调度模型进行求解．

相比一般的最短路径规划问题，共享单车的调度路径规划涉及每个站点的调入与调出量的决策，由于调度车的容量的限制，每个站点的决策将对下一个站点的决策产生影响．Ho等[15]早已证明共享单车的调度路径规划属于NP-hard问题，常采用启发式算法对该类问题进行求解．

考虑到在规划调度方案时，若以整个北京市为调度服务区，区域内站点数量庞大，对算法的求解速度具有较高的要求．因此，采用爬山性较强、搜索速度快的禁忌搜索算法(tabu search, TS)对算例进行求解，算法的基本流程见图5．

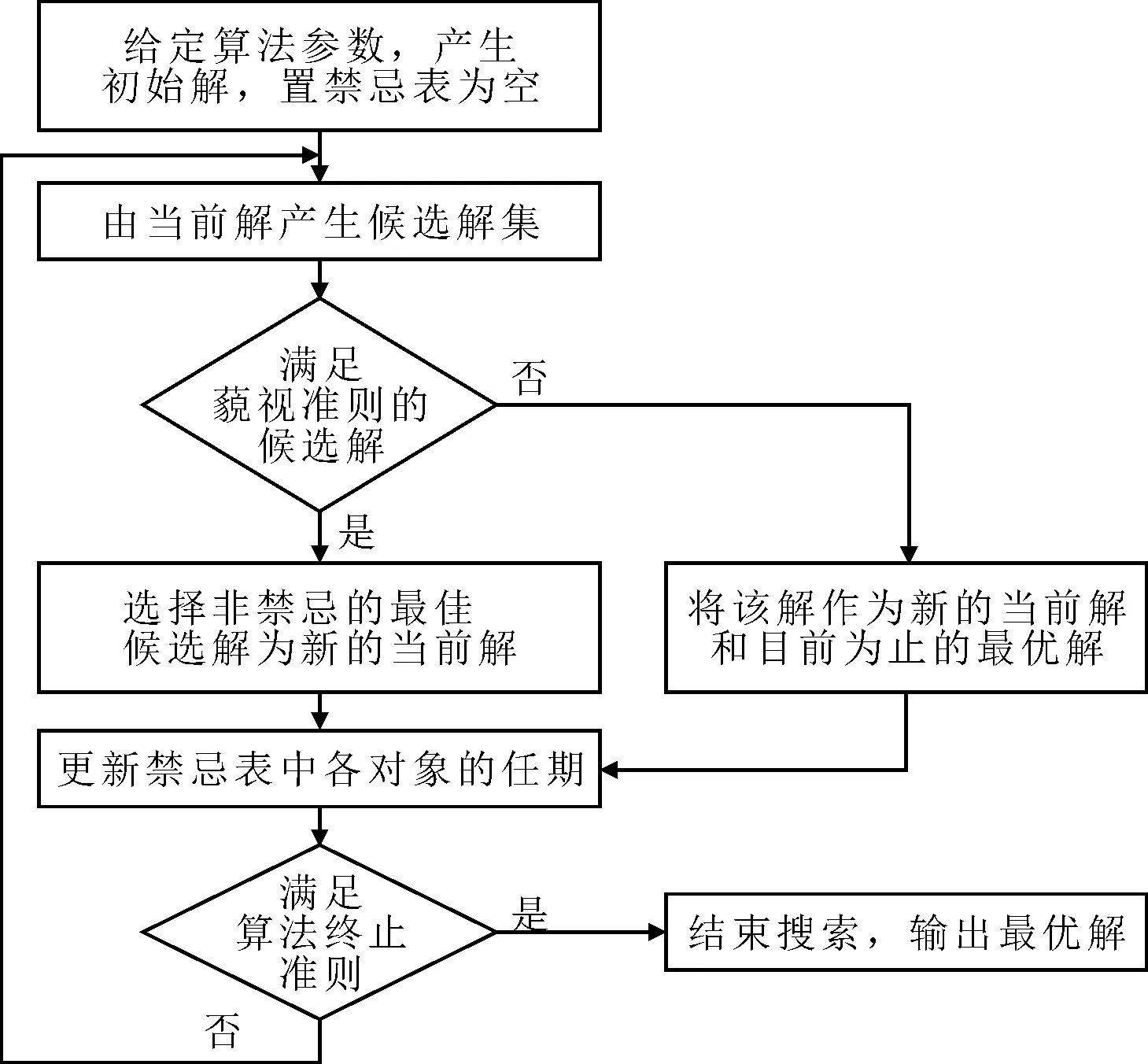
图5 TS算法流程

以最短路为初始解，当调度车的数量分别为1、2、3、4辆时，最优解见表5.

由表5可知:对于Geohash编码为wx4eh的区域，当调度车的总量不超过3辆时，由于在调度成本中引入了惩罚成本，随着调度车的增加，区域内的调度需求的满足程度增加，调度成本随着惩罚成本的降低而降低．由于3辆调度车的初始装载量可满足该区域的调度需求，因此，当调度车为4辆时，随着调度车的折旧成本和作业成本的增加，调度成本开始变大．在本算例的假设情形下，wx4eh区域内设置3辆调度车，以上表的最优路径执行调度的成本最低．同样的，对于上层调度区wx4e，采用区间调度模型规划出调度车在各中层调度区间的调度路径，从而实现对整个北京市的摩拜单车的调度作业．

表5 最优调度路径

为进一步验证本文方法的可靠性，同样的采用TS算法，针对上述案例，分别对文献[8]中提出的分层调度模型与本文模型的求解迭代过程进行对比(调度车设为3辆)，结果见图6．

图6 不同调度模型的收敛速度对比结果

由于本文目标函数中调度成本与文献[8]的衡量指标的不同，只比较两者的收敛速度．由图6可知:本文提出的共享单车分层调度方法在迭代50次时开始进化收敛，收敛速度显著优于文献[8]所提出的模型．由此表明，以同样的算法进行求解时，本文所提出的调度模型的时间复杂度较低，适用于实际调度应用．

4 结 束 语

基于VRP理论，针对传统调度方法忽略了调度区的整体供需失衡的不足，提出了一种分层调度策略．通过Geohash地理编码和用户骑行订单数据分析，以编码位数为4、5、6将共享单车调度服务区划分为上、中、底三层，每层调度区内设有调度站和对应的调度点，并建立区间调度模型规划每层调度区内的调度路径．

以Geohash编码为wx4eh的区域为区间调度案例，以24h为调度周期，通过骑行历史订单数据确定调度需求，采用禁忌搜索算法求解出不同初始调度车数量下的最优调度路径．案例分析表明：所提出的分层调度方法和区间调度模型可有效的对共享单车的调度方案进行规划，对比已有的分层调度方案，求解过程的收敛速度更快，模型时间复杂度较低．

由于存在高峰期的调度点的容量小于用户需求的情形，需针对不同调度点设置不同的调度周期，待下阶段的研究进一步展开．