基于客货共运模式的地铁物流路径优化

2022-07-11郑长江

贵州大学学报(自然科学版) 2022年4期

张晨，郑长江

(河海大学土木与交通学院，江苏南京 210098)

随着城市化的快速发展和人民生活水平的不断提高，人们对邮政快递业务的需求日益增长。国家邮政局数据显示，2020年，我国邮政行业业务收入(不包括邮政储蓄银行直接营业收入)累计完成11 037.8 亿元，同比增长14.5%；业务总量累计完成21 053.2 亿元，同比增长29.7%。伴随着高速增长的物流业务，城市道路交通的使用状况日益紧张。大量物流车辆占用城市道路所造成的拥堵以及伴生的噪音污染、尾气污染等问题，使得积极探索新型城市物流配送方式显得十分必要。《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要》中指出，应当构建高效实用、智能绿色、安全可靠的现代化交通运输体系和物流网络。《交通强国建设纲要》中提出，应当促进城际干线运输和城市末端配送有机衔接，鼓励发展集约化配送模式，积极发展城市地下物流配送。而城市中快速构建的地铁交通网络，由于其特有的客流时空分布特征，为物流配送方式向地下空间的探索提供了可能性。

利用地铁进行物流配送正受到越来越多的关注和重视，相关研究已具备现实意义和可应用性。2012年， MOTRAGHI等[1]通过纽卡斯尔市利用地铁运输货物的案例，研究了利用地铁进行城市货物运输的可行性；2015年，ANAND等[2]概述了城市物流的相关建模工作；VIEIRA等[3]研究了各种货运分配结构之间的相互作用；胡迪等[4]实地调研了上海地铁在客运低谷期进行客货共运，以及在夜间停运期进行货物运输的可行性；2017年，陈梓毓[5]利用南京地铁进行配送的可用时段和运力，从技术层面和流通要素角度探究了利用地铁进行物流配送的可行性；2018年，周芳汀等[6-8]构建了软时间窗限制下地铁配送网络路径优化模型，并设计随机变邻域的迭代搜索算法(iterated local search and random variable neighborhood descent,ILS-RVND) 进行求解；华云等[9]利用解释结构模型(interpretative structural modeling mode,ISM)分析地下物流节点选址影响因素之间的关系，研究地下物流节点选址的一般规律；2019年，刘亚楠等[10]以南京市地铁2、4号线为例，利用多目标优化模型和改进遗传算法，优化了基于地铁的地下物流配送路径；杨婷等[11]在刘亚楠研究的基础上，进一步研究了带时间窗的地下物流路径优化；2020年，陈一村等[12-14]提出了地铁与地下物流系统协同运输的3种可行方式，并运用K-means聚类和Dijkstra算法分别定量分析其对城市地铁客运和地面物流配送的影响。上述研究对基于地铁进行城市物流配送提出了很多建设性的意见和方法，但是缺少在客户时间窗的限制下，对于客货共运模式地铁的配送路径优化研究。

本研究以客货共运的地铁线路作为物流配送的主干，考虑在客户时间窗的限制下，对单个站点附近的客户进行末端物流配送的路径优化问题，通过改进遗传算法对模型进行求解。最后，以南京市地铁4号线为例，对模型进行验证。结果表明，相较于城市内单一的货车配送，利用地铁线路进行物流配送，可以大幅度地降低配送成本，提高配送效率。

1 客货共运特征分析

客货共运是客货共线模式的一种，指通过同一列地铁的不同车厢，分别实现运客和运货的目的。在该种模式下，所花费的建设成本仅为增设地铁外挂车厢和额外建设货仓，所考虑的运营影响仅为确保乘客与货物出入地铁在时间上的一致性，以及对站台上人流和物流的引导。该运输模式具有较低的建设成本、较小的运营影响以及较高的安全可靠性。

同时，在利用货仓临时储存货物时，还需考虑货物在地面与地下的转运问题，以及货物的整理、配货、封装等问题。这需要依据各个地铁站的地理条件、富余空间、转运设备等条件，判别其改造的可行性与建设成本。其运营方式如图1所示。

图1 地铁客货共运示意图Fig.1 Schematic diagram of passenger-and-package sharing transportation by subway

地铁上的白色方格代表客运车厢，其中的乘客通过客运站台出入地铁。灰色方格代表货运车厢，其中的物流货物通过货仓出入地铁。

2 问题描述与建模

2.1 问题描述与符号说明

问题描述：货物由城市物流配送中心，通过货车运送至地铁物流转运中心，再经由客货共运模式下的地铁运送至各个指定出站口，最后通过城市物流配送车辆送到各个客户手中，配送车辆运送完成后需要返回至出站口。其中，地铁线路已知，配送中心位置、地铁物流转运中心位置、出站口位置和客户位置都已知，客户需求、收货时间窗和服务时长已知，各节点转运时长已知，城市物流配送车辆的容量限制已知。

模型假设如下：

1)仅有一个配送中心和地铁物流转运中心，货物从配送中心立即发出；

2)在地铁运输过程中所装载的货物不超过其最大容量限制；

3)利用地铁进行客货共运对地铁乘客的服务质量无影响；

4)各个出站口所服务的客户范围固定；

5)货物送达时间满足客户的时间窗要求。

根据以上对模型的描述和设定的假设，现定义参量和变量，如表1所示。其中，由配送中心和各转运节点排序组成的路线方案为决策变量。

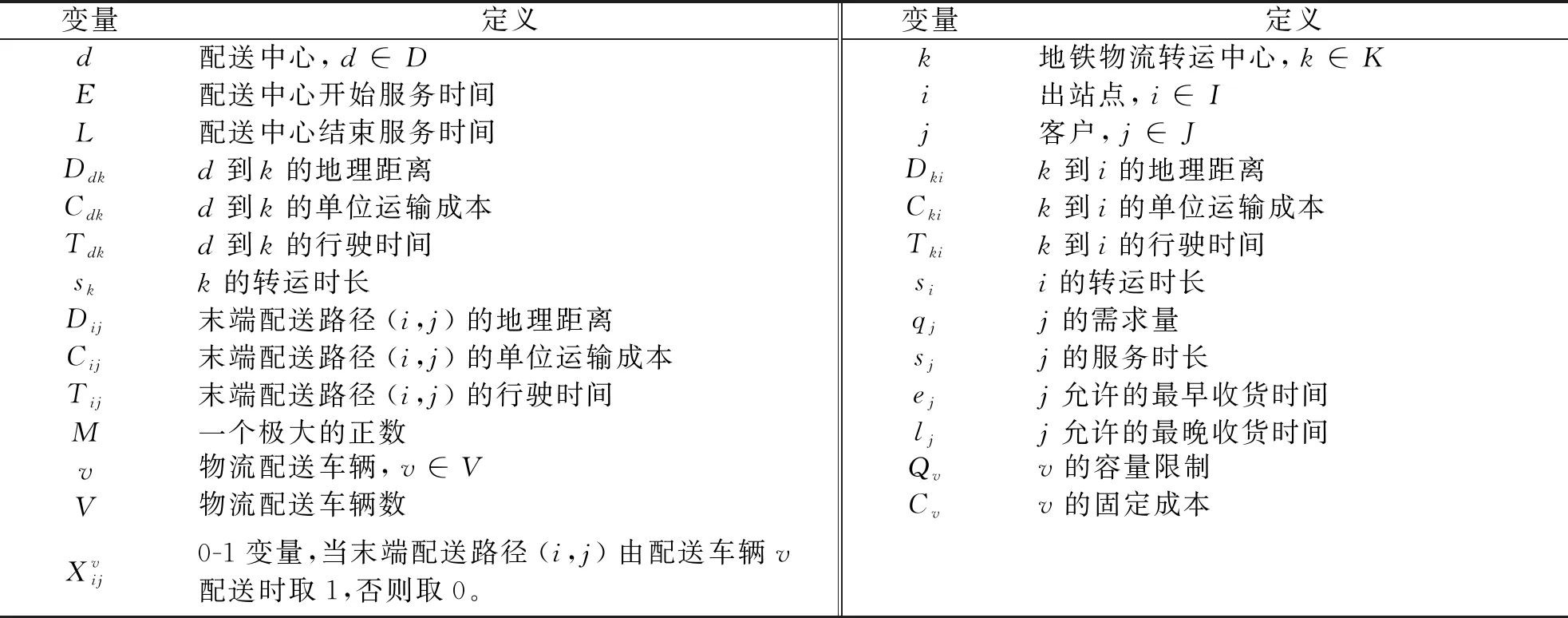
表1 参变量定义表Tab.1 Parameter definition

2.2 模型建立

(1)

(2)

(3)

(4)

∀d∈D,∀k∈K,∀i∈I,∀j∈J,∀v∈V

(5)

∀j∈J,∀v∈V

(6)

E≥0,L≥0,V≥0

(7)

sk≥0,si≥0,sj≥0,ej≥0,lj≥0,∀k∈K,∀i∈I,∀j∈J

(8)

(9)

其中，式(1)为目标函数，表示以总成本最小为目标，第一部分是货物从配送中心发出，经由货车和地铁运送至出站口的成本；第二部分是末端节点配送成本和城市物流配送车辆的固定使用成本。式(2)是指每辆配送车辆对其配送线路上的客户只经过一次。式(3)是指配送车辆的总数。式(4)表示每条配送线路上所有客户的需求量总和不得超过配送车辆的容量限制。式(5)是指客户j的最早服务时间与配送中心开始服务时间之差不得小于该线路上的固定时间成本。式(6)是指在同一条线路上，相邻两个配送时间窗的限制。式(7)和式(8)是指决策变量的非负整数约束。式(9)是指决策变量的0-1约束。

3 求解算法

遗传算法的基本原理[15-16]是先随机产生一个初始种群，确定该种群中的最优个体为最优解，然后对该初始种群进行迭代优化。优化过程：计算种群适应度值，选择出较优个体作为子代，与父代基因进行交叉操作生成新的子代，并对新的子代中的个体进行变异操作，获得最终的子代种群；将新的子代种群与初始种群进行优劣比较，判断其能否替代初始种群。重复以上步骤，直至迭代结束，获得最终的局部最优解。

对遗传算法进行改进，具体操作步骤如下：

1)生成初始解

将出口站固定范围内的客户随机排列顺序，依据客户需求量和载具容量限制，生成若干个起讫点作为出口站的配送路径，且各客户点不重复配送，计算配送总成本。在种群中寻求总成本最低的个体作为最优解。

2)计算适应度

种群中各个个体的适应度值为目标函数值的倒数，将寻找目标函数的最小值转变为寻找适应度函数的最大值，作为后续步骤的评判标准。

3)选择

依据个体适应度值，对种群中的个体进行升序排列，通过轮盘赌的方式，选择出适应度大的个体，作为子代。其中代沟设置为90%，即父代种群中有90%的个体将被子代代替。

4)交叉

对子代两两进行交叉操作，以90%的概率随机选择两个体，将对应位置的基因片段进行交叉，再检查交叉后的个体是否存在基因重复片段，若存在，则对其进行更改。生成新的子代。

5)变异

在新的子代中以5%的概率随机选择两个基因，调换位置，作为变异操作。

6)局部搜索

对每一个个体中的配送路径进行其邻近域的路径搜索，生成新的路径，判断新路径是否更优，若是，则作为当前解。

具体流程如图2所示。

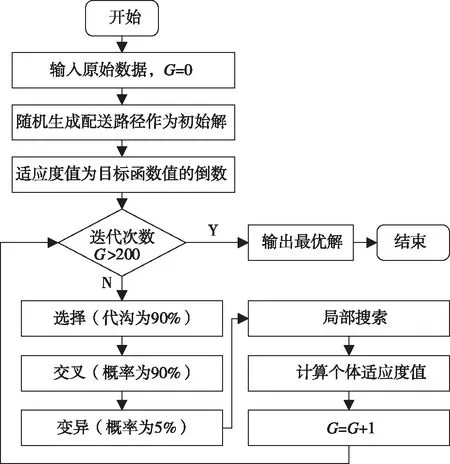
图2 遗传算法流程图Fig.2 Genetic algorithm flowchart

4 实例计算与结果分析

4.1 实例数据

如图3，以南京市地铁4号线为例，该地铁线的运营时间为每日6：00—23：00。假设配送中心的运营时间为每日5：30—22：30，货物从配送中心发出，由城市物流配送车通过城市道路运至地铁转运中心(聚宝山站)，运输距离(Ddk)5.9 km，配送车辆均速42 km·h-1，容量限制(Qv)200件，单位运输成本(Cij)2元·km-1，固定运营成本(Cv)为5元·辆-1。在聚宝山站通过时长(sk)30 min的转运，利用地铁运送至出站口(云南路站)，运输距离(Dki)10.6 km，运输时长(Tki)18 min，单位运输成本(Cki)0.1 元·km-1。在云南路站经过时长(si)30 min的转运，由城市物流配送车，运至各个客户点。

图3 南京地铁4号线沿线物流节点示意图Fig.3 The layout of logistics nodes along Nanjing Metro Line 4

图中以云南路为坐标原点，东方为x轴，南方为y轴。客户点分布在地铁4号线沿线两侧。

各个节点信息包括：节点的位置坐标、客户点货物需求量、节点服务时间窗以及转运节点和客户点的服务时长。节点信息如表2所示。

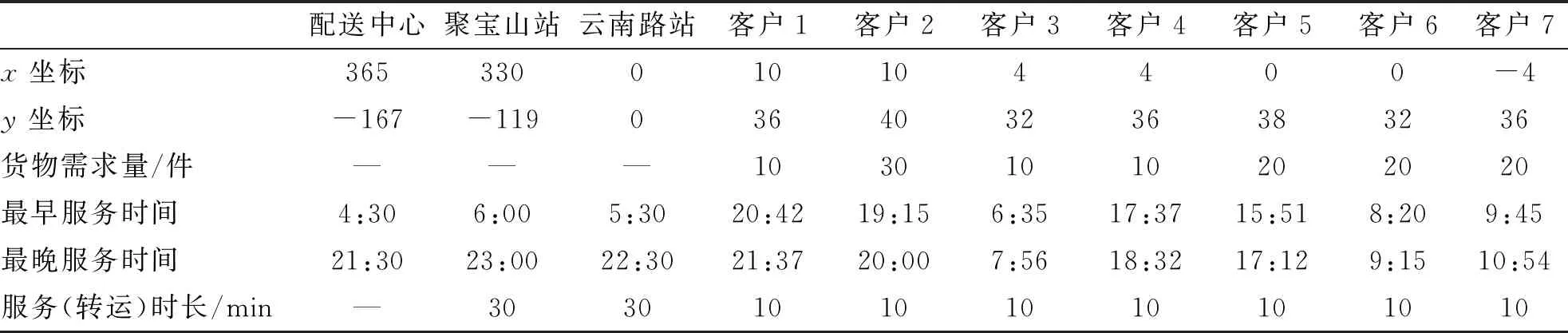
表2 各节点初始信息Tab.2 Initial information of each node

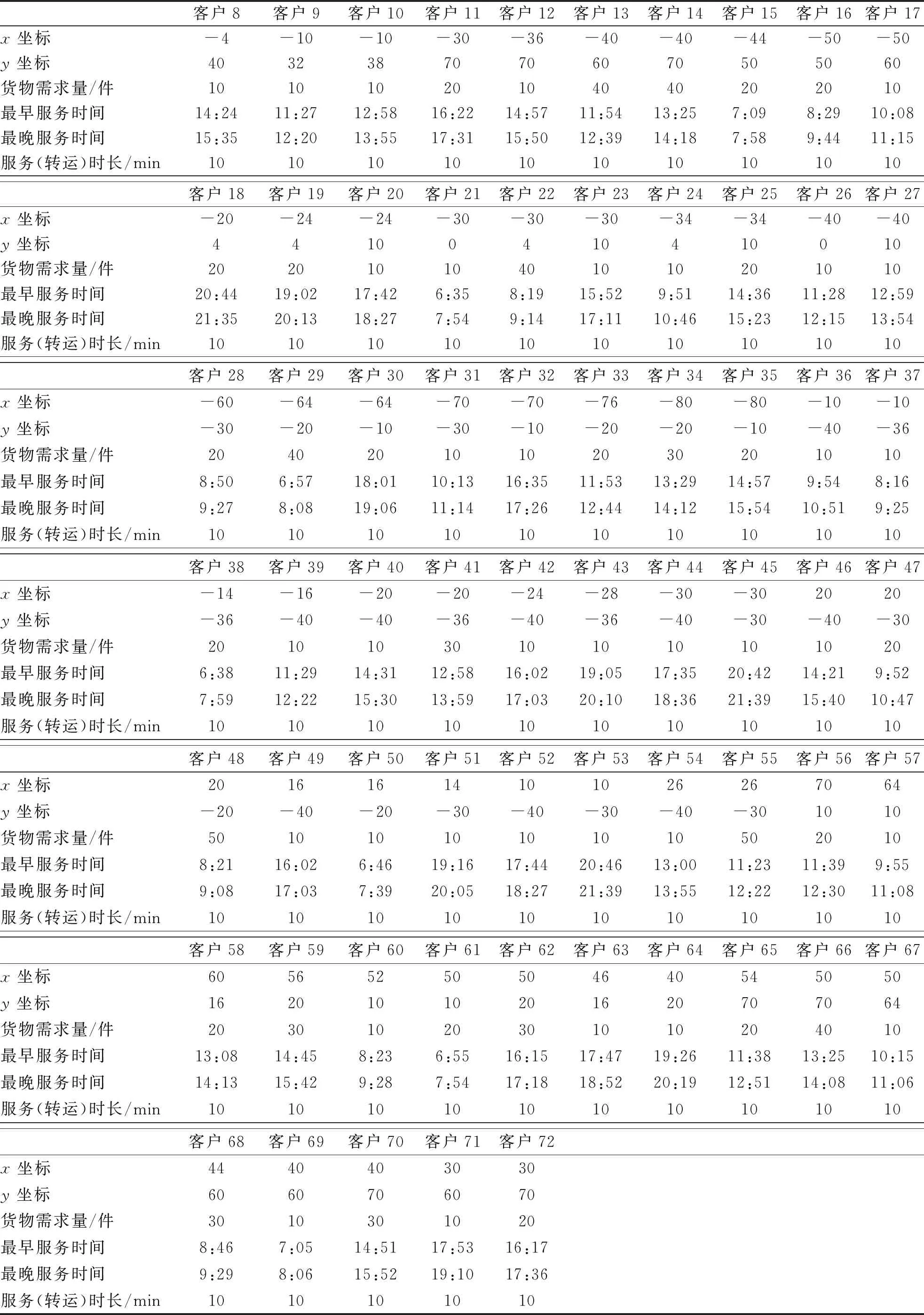
续表

货物从配送中心发出，经由聚宝山站，到达云南路站。云南路站的服务时间为5:30至22:30，转运时长为30 min。最后由云南路站进行终端配送，将货物送至各个客户点。

4.2 结果分析

利用Matlab软件，采用遗传算法(genetic algorithm)对该带时间窗的配送路径优化问题进行求解，分别计算基于地铁网络进行物流配送和仅基于货车单独进行物流配送两种情况下的最优方案，最终配送路径信息如表3和表4所示。由表3可知，利用货车从配送中心进行货物配送，所得到的最优方案共有7条配送路径。由表4可知，利用货车从云南路站进行货物配送，所得到的最优方案共有8条配送路径。

表3 基于货车的物流配送路径Tab.3 Logistics distribution route based on truck

表4 基于地铁的物流配送路径Tab.4 Logistics distribution route based on subway

基于地铁进行物流配送的优化过程如图4，以总成本最低为优化目标，经过100次迭代后，种群适应度值降至100上下，并趋于稳定。可知迭代次数设置为100次，已满足优化需求。最优方案配送路线图如图5，以地铁出站口(云南路站)为起点，在满足各个客户点收货时间窗的条件下，以总成本最低为目标，经过100次优化得到的8条配送路径图。

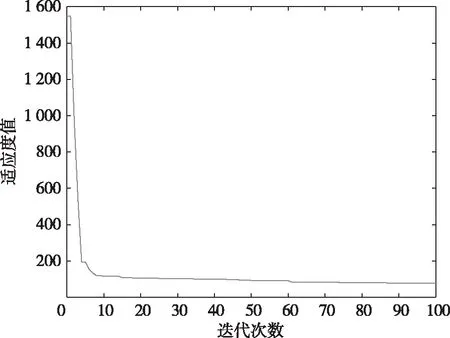
图4 基于地铁的优化过程Fig.4 Optimization process based on subway

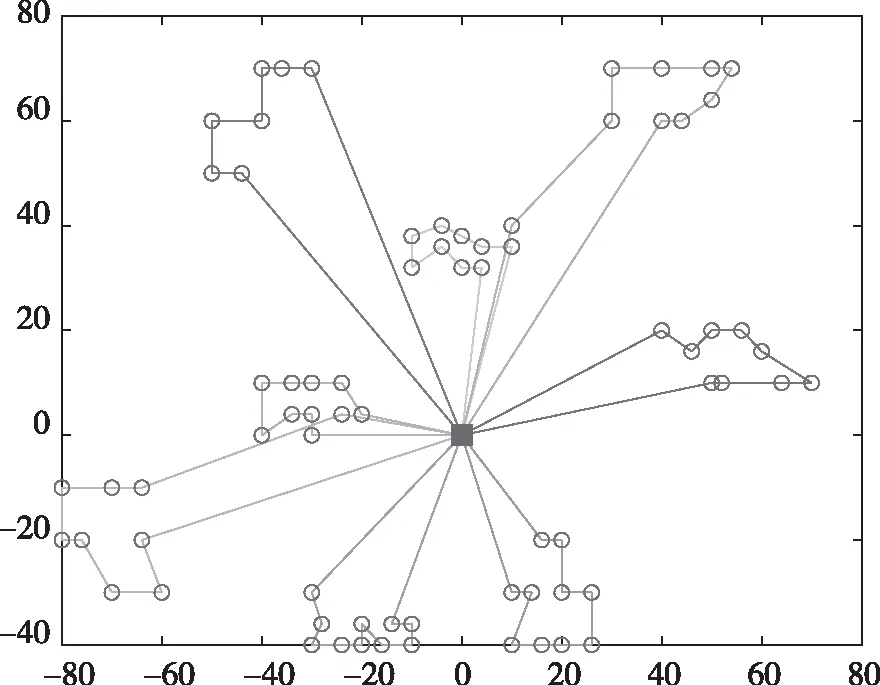
图5 基于地铁的最优配送方案路线图Fig.5 Roadmap of optimal distribution plan based on subway

利用货车单独进行货物配送与基于地铁的物流配送，这两种方案的对比如表5所示。

表5 两种配送方式最优方案比较Tab.5 Comparison of the optimal schemes of the two distribution methods

表5从总成本、配送距离和平均花费时间3个方面进行方案对比。相较于仅使用货车进行物流配送，在基于地铁进行货物运输时，运送的各项指标都有了极大的改善。其总成本由255.1 元降低至91.1 元，降低了64.29%；配送距离由110.0 km缩短至35.6 km，缩短了67.67%；平均花费时间由157.2 min缩短至113.7 min，缩短27.67%。可见，相较于货车运输，利用地铁进行物流配送具有更低的运营成本和更高的综合效率。