古典时期键盘音乐基于优律的猜想与实证探讨
2022-07-11余思韵






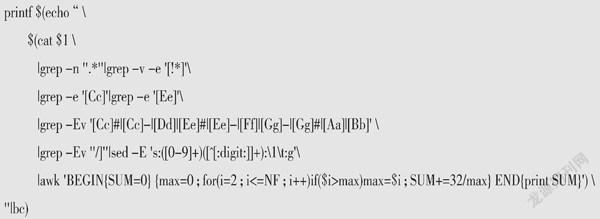




THE USE OF MAJOR THIRD AND ITS CORRELATION WITH WELL-TEMPERAMENT IN
MOZART’S AND BEETHOVEN’S PIANO SONATAS
摘 要:有学者认为,从巴赫到肖邦都是优律的时代。巴赫使用的并非平均律已有良多讨论,也有材料显示,莫扎特、贝多芬,乃至19世纪的调律师都体现出对非平均律制的认同。对莫扎特19首、贝多芬32首钢琴奏鸣曲中大三度使用量的统计显示,某些大三度比另一些大三度更常用,且大三度的使用量与在优律中大三度的大小成反比关系。两人钢琴奏鸣曲的大三度使用量与18世纪下半叶各优律大三度音分值的线性回归显示,当时音乐家们对键盘律制有共同追求且律制之间有继承的可能性很大。
关键词:贝多芬;莫扎特;优律;大三度;渐变三度律;钢琴奏鸣曲
中图分类号: J624.1 文献标识码:A
文章编号:1004-2172(2022)03-0088-18
DOI:10.15929/j.cnki.1004 - 2172.2022.03.010
在18世纪的音乐实践中,存在着一些混合不同大小的五度调制而成的律制,它们和平均律一样能实现24个大小调贯通使用,但又因为各和弦有不同的抖拍而拥有平均律所没有的调性色彩对比,人们称之为“well-temperament/优律”。像非平均律一样,优律是一种类称,不是特指某一种律制。巴赫的键盘曲集Das Wohltemperierte Clavier的名称所指的也是“well temperament/优律”而非“equal temperament/平均律”,但中文一直沿用“平均律”的翻译,可见在国内人们并没有意识到此中存在某种误解,或者没有引起重视。而西方学界在20世纪下半叶和21世纪初,围绕巴赫所用优律的问题已经有过两次规模不小的讨论,赫伯特·安东·凯尔纳①、约翰·巴恩斯②、马克·林德利③、布拉德利·莱曼④、约翰·查尔斯·弗朗西斯⑤等若干学者均就此提出了各种证据,并发表了自己认可的巴赫优律方案。
律制的使用势必对音乐风格有所影响、对音乐创作有所规限。诸如阿拉伯的微分音、中国西北的欢苦音等,这些特别的音律产生了偏离常规的特殊色彩和别有意味的表达,姑且勿论是先有这些音律还是先有特殊的表达需要,实际的调律都是获得这些色彩、实现这些表达的必要基础。而后人对之前某个历史时期律制使用状况的了解,则会影响其对该时期音乐音响效果的想象以及对当时音乐家某些创作特征的认识。例如明确知道巴赫所用的键盘律制,就有助于更深入细致地理解他的48首前奏曲与赋格以及其它键盘作品的不同写法及其表现力。事实上,目前的研究已初步揭示出,在巴赫音乐创作的年代——18世纪上半叶,欧洲键盘乐器调律采用的是优律。那么,巴赫之后古典主义时期的键盘音乐是否也基于优律?在此以一项对莫扎特、贝多芬钢琴奏鸣曲大三度使用量的统计分析及其与优律大三度大小的相关性研究,来对这一问题进行探讨。
一、研究假设:来自文献的史实依据
到了18世纪下半叶,欧洲的键盘调律其实仍未定型。1744年,乔治·安德烈亚斯·佐尔格①
提出了一套律制,并于1750年造出两尺长的测弦器拿到莱比锡市场上出售②,1758年又提出了相似的供卡莫顿管风琴所使用的律制③。相继地,1762年,焦尔达诺·里卡蒂④发表了一个他认为符合当时实践的律制⑤。1774年,約翰·海因里希·朗伯⑥提出要把毕达哥拉斯音差分成7份放在F—C—G—D—A—E—B—F 的7个五度上⑦。1776年,费里德里克·威廉·马普格⑧发表了调音调律文献《论乐律》⑨,不仅呈现了以纯律为基础的测弦器,还提出了若干套能调出非常接近平均律音律的调音法。1777年,让·巴普蒂斯特·梅卡迪耶⑩提出过一种律制,和汤玛斯·杨的律制很像。1771年,巴赫的学生和追随者约翰·菲利普·基恩贝尔格提出了基恩贝尔格第Ⅱ律;1779年,他又提出了基恩贝尔格第III律。除这几人之外,弗朗切斯科·安东尼奥·瓦洛蒂①
也提出了一种律制,可以说是18世纪几种重要的优律之一,研制于1754年,发表于1779年。②
巴伦·冯·维泽③在《声音、发音和调律的分类》④中一共提出了4种律制。⑤贝多芬同时代的英国人托玛斯·杨⑥在1800年提出的律制与内德哈特的第1号循环律非常相似,与弗朗切斯科·安东尼奥·瓦洛蒂1779年提出的律制也仅是在两个音上有2音分的差异。(详见表1)
从表2中大三度的音分值来看,这些律制大体分成两类。第一类是大三度呈有序渐变的,第二类是近似平均律的。第一类其实就是优律,除了费里德里克·威廉·马普格,其他人提出的律制都属这类。这类律制虽然对称轴(即“最小大三度—最大大三度”)和渐变斜率有所不同,大三度的渐变倾向却很清晰,支持了詹姆斯·默里·巴伯提出的以渐变三度律作为优律理想模型(详见下文)的合理性。除了巴伦·冯·维泽的两个律制之外,其他律制中F、C、G这3个音上的大三度均是最小的,最接近纯律大三度。WIESE-No.3更像是“相反的中庸全音律”,4个大三度为408音分,另外8个为396音分,说“相反的”是因为像B—D、F—A、C—E、G—B这些在中庸全音律中本该较窄的大三度在这里反而是最大的。WIESE-No.1的大三度大小两极分化比较严重,有6个偏大的大三度。WIESE-No.1最大的大三度位于D、A、E、B、F和C上,WIESE-No.3最大的大三度则位于B、F、C和G上,与其他律制相反。第二类就是费里德里克·威廉·马普格的11种律制,其中有5种都有均等的400音分大三度,另外6种的大三度偏离也不大,且排列相对杂乱,显然他的思路更倾向于平均律。
可见,在18世纪下半叶,平均律还未成为调音的泛用标准,而且支持优律的人更多。
除此之外,一些历史线索也很能说明问题。海顿对查尔斯·克拉格特的专利——每个八度分成39个音的钢琴(Telio-chordon)——赞誉有加,他认为,虽然可能要花一些时间来熟习键盘布局,但这种键盘对音律的呈现是普通十二音键盘所难以企及的。⑦在莫扎特学生托马斯·亚特伍德的笔记本里,记录了莫扎特对大半音和小半音的手写标记,清楚地显示了莫扎特认为半音并不都是平均的。⑧巴赫的儿子C.P.E.巴赫在《论键盘演奏的真正艺术》中描述楔锤键琴与羽管键琴的调音时,只是提到调节“大多数的”五度而非“全部的”五度,此外,他还提到某些调在键盘乐器上的听觉效果比在非键盘乐器上的更为纯净。①德国著名的音乐出版商、经纪人海因里希·菲利普·卡尔·博斯勒在他1782年出版的《音乐艺术初级教程》中提出②,可以先把一个八度分成3个均等的部分,如C—E—G—C,然后根据每个大三度调出相应的4个稍微窄的五度。这样的调音貌似能够调出平均律,不过,可能是他自己也认识到人耳辨音并非那么的可靠,所以他还是推荐读者去买来自法兰克福或者莱比锡的十二音音叉。曾在1818年送过一架钢琴给贝多芬的乐器制造商布罗德伍德(Broadwood),直到1841年才逐渐开始尝试把所造的钢琴调成平均律③(有学者认为,那时调的并不是平均律)。贝多芬的传记作者和抄写员安东·费利克斯·辛德勒曾提及,贝多芬在一定程度上接受对钢琴独奏和三重奏的调色彩描述,美国音乐学家罗斯·达芬认为,这是贝多芬根据其钢琴上某种非平均律思考的结果。④美国学者詹姆斯·默里·巴伯在研究平均律演变历史时,梳理出一系列“复划分体系”①以及70多种不规则调节律,佐证了优律曾一度繁荣这一说法。欧文·乔根森在1977年写道,“1854年通常被认为是欧洲音乐世界最终并完全采用平均律的大致转折点”②。更重要的证据是,亚历山大·艾利斯在翻译赫尔曼·冯·赫尔姆霍茨《论音感》时,邀请了7位当时著名的调律师进行实验,发现他们调的都不是平均律③。
综上所述,莫扎特、贝多芬时代的键盘使用优律的可能性是很大的。但目前尚未发现对两人用律的直接描述,笔者试图从他们的作品中寻找线索。
二、研究设计:基于数字化乐谱的统计分析
自文艺复兴时期起,人们越发重视三度、六度音程的使用,为了保证大三度的听觉品质而牺牲五度纯度的中庸全音律的出现就是有力的证明。但文化的变迁、音乐风格的更迭都有过渡时期,原有的习惯在新时期会有所延续。在纯律中,大三度音程的冠音正好是音程根音的泛音之一,在调准的情况下,两音同时发声不会产生抖拍,有稍微音准偏差的大三度则会有较慢的抖拍,而不好的或者跑调的大三度则会产生较快的抖拍。两音同时发声的时值越长,节奏越慢,抖拍越容易被听出,即音程中的“不準”越容易被辨认出来。所以,除非有特别的意图,否则,习惯于纯律音响的音乐家们在时值越长的音符上想要的应是越接近纯律的大三度。人们对纯律的听觉审美在中庸全音律时代有所延续,四分之一中庸全音律也正是因为其中有8大三度最接近纯律的音响而获得了大批支持者。
然而,在中庸全音律中,前11个五度被收窄,致使最后第12个五度变成了“狼音五度”。宽出的“狼音五度”是跑调的,少则宽出15音分,多则宽出55音分,所以凡是包含这个五度的音阶便不能用了。音乐家们不得不被限制,只能在少数可用的调上进行创作。所以人们想方设法去突破,优律和平均律都是解决方案。
平均律是“一刀切”的,全部大三度都“跑调”④,而优律的情况则不同,由于可以混合使用不同大小的五度,所以其三度的大小自然可以有不同的变化。詹姆斯·默里·巴伯认为,维克迈斯特、内德哈特等人所设计的各种律制,无论是改良的中庸全音律还是优律,都体现出他们想要让常用的调听上去更接近纯律,而不常用的调可以“跑调”多一些的想法⑤。
10个指头有长短,既然优律12个大三度有优有劣,音乐家们在使用时必定有所偏倚。人们在调制中庸全音律的时候,保留有对纯律大三度听觉审美的惯性。那么在使用优律时偏向更纯的大三度也合乎情理。约翰·巴恩斯⑥认为作曲家会少用甚至不用不悦耳的音程,又或者对这些音程作不同时发声的分解处理以弱化冲突,他通过对巴赫24首大调前奏曲中大三度的形态进行分析,发现巴赫使用大三度的规律与维克迈斯特第III律中大三度的纯度趋势大致吻合,越纯的大三度被使用得越多,所以他认为巴赫当时用的可能是维克迈斯特第III律。
所以,可以合理推断,如果在18世纪下半叶优律确实存在且更受支持,那么莫扎特、贝多芬对大三度的使用应该也会像巴赫的那样,呈现出一定的规律——更纯的大三度用得更多。
(一)目的与方法
莫扎特的19首钢琴奏鸣曲、贝多芬的32首钢琴奏鸣曲是钢琴学习者的经典曲目,数量有一定规模且具有代表性。本研究将分别对两人所有奏鸣曲中的12组大三度的使用量进行统计,并观察他们大三度的使用量与大三度的大小之间是否存在关系。
考虑到作品篇幅长大,人手统计耗时漫长,所以笔者运用了计算机程序来辅助。Humdrum Toolkit①是由大卫·休伦(David Huron)于20世纪80年代开发的音乐分析工具,其中包括.kern格式的数字化乐谱及可以利用C++、Python等计算机语言进行二次开发的分析软件。本次分析就是基于.kern格式的数字化乐谱进行的。
.kern格式是把五线谱中的音高、节奏等信息转化为数字、字母、符号等组合,以方便计算机进行运算。这种乐谱格式以时间为顺序往下展开,相当于把从左至右的五线谱变成从上往下的纵向形式,每一行表示新的音符或休止符出现的一个节点,如图1中的框选所示。
部分符号标记示例见表3。在乐谱之前,还可以通过注释行补全作曲家、作品集、作品号及相关版权的信息。需要注意的是,在图1中,每行谱只有一个声部,所以一共只有两列,若有双音或多声部则可以通过增加相应数量的列来表示,例如有3个声部就分三列,如此类推。要注意“.”的作用,如图1第4小节第1拍,左手低音谱号第1个音是四分音符的D,“4D”,而右手第1个音是八分音符的a,“8a”, 右手第2个八分音符出现时左手“D”的声音依然在延续,所以用“.”来表示,以此可区分是新出现的音符还是延续上一音符的声音。装饰音等会由其他特殊符号表示①。
(二)数据的采集
首先,要明确哪些情况需要纳入统计。一个八度有12个音,以C音为例,要统计的是C—E大三度的使用量,分为如下几类:
1.同时出现的,只包含C和E、不包含其他音符的大三度,转位的六度及超过八度的复音程及也纳入统计。由于旋律音程是两音先后发声的,不会出现声音叠加,不纳入统计。带有延留音的大三度,如C音先出现,然后在其延留的过程中出现E音,在这种情况下,先出现的声波经过了一定时间的减弱,这样即便有抖拍也会被弱化,所以也不纳入统计。
2.考虑到在实际作品中只用三、六度音程的情况相对较少,包含大三度的三和弦及其转位也可以纳入统计范围。大三和弦与小三和弦中均包含大三度,但是三和弦更多强调三音的色彩,大三和弦中强调的是大三度,而小三和弦强调的是小三度,所以在统计中只包括大三和弦而排除小三和弦。对于七和弦及其他不协和和弦,其中所包含的二度是产生不协和听觉效果的主要因素,所以均排除在外。
以莫扎特《第一号奏鸣曲》第一乐章前9小节为例,谱例1中框出的音程与和弦会纳入统计。
其次是要明确统计的单位。约翰·巴恩斯②和米歇尔·迪盖③都是先统计出现的次数,然后再按照一定的重要性进行加权。但是,这样的权重是由文章作者自己提出的,并非作曲家本身的意愿,并不客观。考虑到时值会影响听众对抖拍的辨认,而且时值也是由作曲家亲自决定的,所以笔者认为用作品中大三度出现的时值来计算更为合理。统计中以三十二分音符为单位,大三度出现的时值有多少个三十二分音符则计数为几。如上例中第一个和弦时值长为一个十六分音符,计数2。这样,所出现的大三度和声音程或大三和弦,其拥有的时值越长其权重越大。装饰音不纳入计数。
(三)实施步骤
利用基于网页的JupyterLab可以编写计算机程序对.kern格式的乐谱进行分析。以统计作品中C—E大三度为例:
第一步,从https://kern.humdrum.org/下载需要分析的. kern格式的乐谱,并设定好文件路径。
第二步,统计出现C—E音程的行。如上文所述,对于需要计数的行,C音和E音必定是同时出现的,而G音是可有可无的,即要选出乐谱中同时出现的“C”和“E”,但不包含除了“G”以外的其他字母以及“C#”“C-”“E#”“E-”的字符组合的行①。由于大字组和小字组的音高会用大小写字母来区分,所以用“[Cc]”命令来表示“无论字母为大写或小写均包含在内”。
第三步,确定所选行的权重。每個时间节点可能出现不同时值的音符,所以一行中可能有表示不同时值的数字。根据. kern格式的设定,时值越小,表示该时值的数字越大,所以只需要把所选行的字母与数字拆分,并选出该行最大的数字,再倒数乘以32,即可得到该行时值等于多少个三十二分音符,这就得出了该行的权重。
第四步,求出一首作品中出现C—E大三度的行的权重的总和。
程序代码如下:
printf $(echo “ \
$(cat $1 \
|grep -n ''.*''|grep -v -e '[!*]'\
|grep -e '[Cc]'|grep -e '[Ee]'\
|grep -Ev '[Cc]#|[Cc]-|[Dd]|[Ee]#|[Ee]-|[Ff]|[Gg]-|[Gg]#|[Aa]|[Bb]' \
|grep -Ev ''/]''|sed -E 's:([0-9]+)([^[:digit:]]+):\1\t:g'\
|awk 'BEGIN{SUM=0} {max=0;for(i=2;i<=NF;i++)if($i>max)max=$i;SUM+=32/max} END{print SUM}') \
''|bc)
对于存在等音的黑键音要分次进行统计再求和。如要统计“C#/D-”上的大三度使用量就需要统计“C#—E#”和“D-—F”两组之和。这组音程还有一种等音可能,重升B—三重升D,但已超出正常用音范围,故不计算。
第五步,求出所有奏鸣曲中C—E使用量之和。
其他音上的统计如此类推。
三、统计结果与分析:对假设的支持
对贝多芬32首钢琴奏鸣曲中大三度使用量统计见图2(以三十二分音符为单位“1”,下同)。
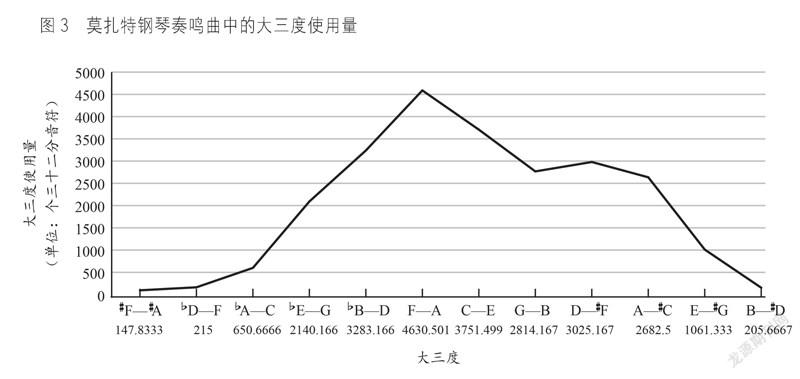
莫扎特19首钢琴奏鸣曲①中大三度使用量统计见图3。
根据图2、图3的统计显示,莫扎特、贝多芬两人钢琴奏鸣曲中大三度的使用量均呈“山形”,有双峰,只是前者峰值位于“F”和“D”,后者峰值位于“E”及“C”上。明显有些大三度较其他大三度更为常用,且呈现出一定的渐变。
(一)与渐变三度律存在高相关
1.渐变三度律——优律的理想模型
詹姆斯·默里·巴伯是美国声学家、音乐学家。他的博士学位论文就是研究平均律的发展史,后来他根据该论文扩写,形成音律专著《调音与调律》(Tuning and Temperament: A Historical Survey)。他研究分析了众多律制之后提出,对于优律,人们想要的其实是从常用调到非常用调大三度呈有序变化的律制,所以提出了渐变三度律——优律的理想模型。他提出的渐变三度律是一种开放式的理论结构:
为了获得有序变化的大三度大小,真正需要的是对所有五度作变量调节而非限定一种大小的五度。设D—A的五度是最窄的,其五度链两侧的五度相继逐渐变宽,最后A上的五度最宽。依次递增的总量为1+2+3+4+5+6+5+4+3+2+1=36单位。因为这些量是分配到12个五度上的……我们可以选择每单位的值以获得想要的大三度大小。如果每单位为1音分,五度D—A为697音分,实际上就是一个中庸全音五度,而A—
E的五度就是703音分,差不多是纯律五度;最优的大三度C—E和G—B是392音分,扩宽1/4音差;最差的大三度G—B和D—F是408音分,正好是毕达哥拉斯大三度①。
按图4所示,若想要闭合五度循环,X和Δ必须满足:12X+36Δ=12×平均律五度=12×700音分;若希望最小的大三度能是纯律大三度,X和Δ就必须满足:(X+2Δ)+(X+Δ)+(X)+(X+Δ)=4X+4Δ=386+2400音分。该模型没有对最小五度的位置和三度渐变的斜率进行限制,音乐家和调律师可以根据对八度、五度和大三度的偏好加以权衡自行微调。
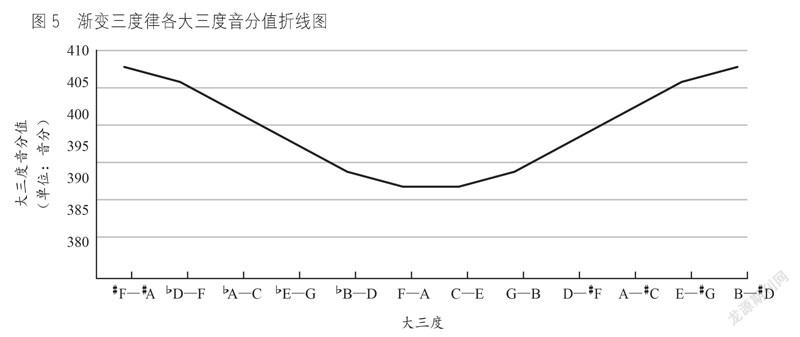
若根据莫扎特、贝多芬的对称轴,把X安排在G—D上,按照上述方法可以算出各音大三度和五度音分值,见表4、表5②。从表中可见,五度大小的变化趋势与大三度大小的变化趋势基本一致。
2.与渐变三度律大三度音分值的相关性分析
对比图2和图5,能看出贝多芬大三度的使用量和渐变三度律大三度的音分值有一定的相关性。
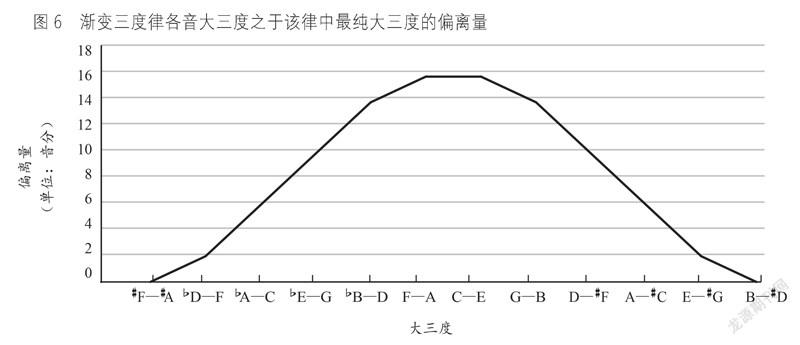
由于各大三度的计算以音分为单位,越接近纯律的大三度音分值越小,而在统计数据中,使用得越多的大三度统计量越大,两者轮廓相反。为了方便从数理上进行验证分析,需先把“山形”倒过来。把各音分值减去集合中最大的音分值,再取绝对值,这样就在不改变递变斜率的前提下把“倒山形”曲线变成了“正山形”,见图6。
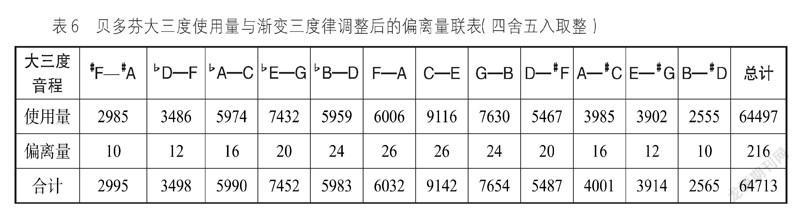
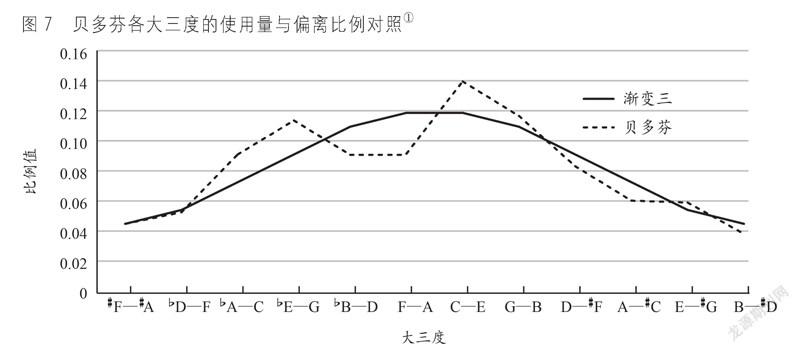
用卡方检验来考察两组数据分段概率结构的相似度,原假设H0为两组数据每个大三度上的值占该组数据总和的比例结构相同。考虑到卡方检验每单元格频数不低于5,或频数大于1且小于5的格数不超过总格数的1/5,而且即便是“最不喜欢的”大三度,贝多芬也有一定的使用。所以根据贝多芬的最低使用量的比例对各值叠加一个基础量,使两曲线处于相仿的水平位置,见表6、图7。
渐变三度律的大三度音分值是Δ的分段一元一次函数,常数的增加减少只改变曲线的高低位置,不改变其斜率,所以不会改变“山形”的坡度。至此,两曲线的相似度已肉眼可辨。
计算得卡方值为6.073,自由度为11,P值为0.868。两组数据各大三度的概率相似程度较高,有86.8%概率可以接受原假设,即有86.8%概率可以认为贝多芬各大三度占所有大三度使用量之和的比例以及渐变三度律各大三度之于该律中最纯大三度的音分偏离占总音分偏离的比例的结构相同。
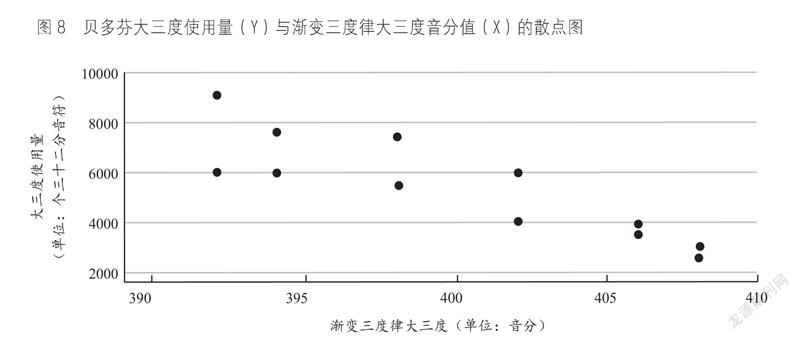
在初步确定了贝多芬大三度使用量与大三度纯度的相关性之后,笔者将对两者进行回归分析做进一步验证。通过绘制贝多芬大三度使用量
(Y)与渐变三度律大三度音分值(X)的散点图(图8),可见两组数据之间具有一定的线性相关。
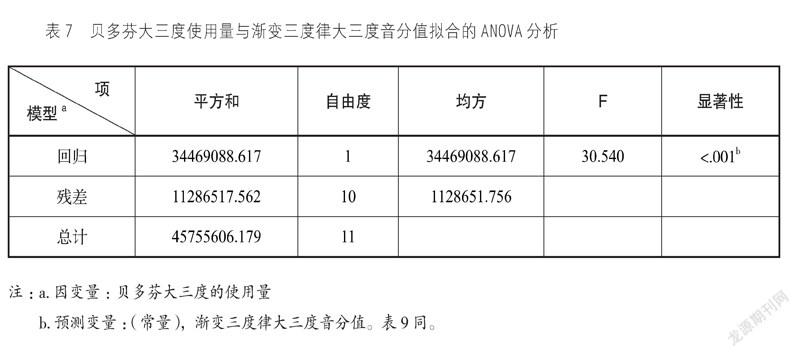
以渐变三度律的大三度音分值为自变量(X),贝多芬的大三度使用量做因变量(Y),进行线性回归分析,可求出Y=120515.294 - 287.851X的回归方程。模型拟合优度R为0.868,ANOVA分析见表7。
0.868的模型拟合优度已经很不错了,但还可以继续优化。在贝多芬的数据中,F和B音有明显的偏离,剔除这两个点后,模型拟合优度上升至0.949,拟合方程为Y=153525.721 - 369.388X。
以上数据表明,贝多芬大三度使用量与渐变三度律大三度音分值有很大的相关性。
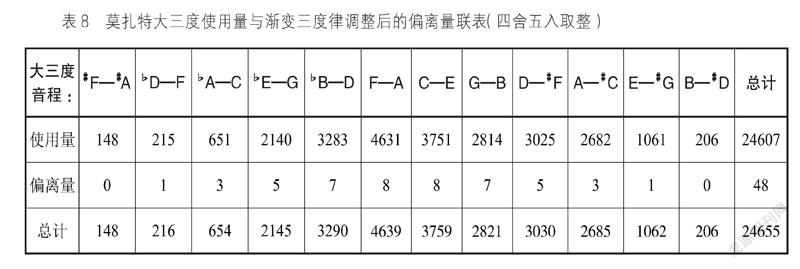
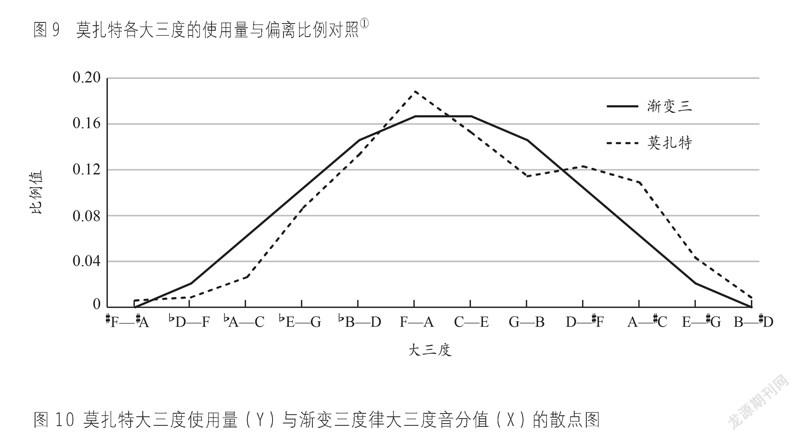
莫扎特的19首钢琴奏鸣曲的大三度数据也显示出相仿的结果。用相同的方式对数据进行处理(见表8、图9),用于与莫扎特钢琴奏鸣曲数据对比的渐变三度律的斜率有所不同,Δ从1音分变成0.5音分,基础叠加值为0,求得卡方值为6.292,自由度为11,P值为0.853。但由于有两个单元格频数为0,6个单元格期望计数小于5,虽然数据很漂亮,但却是无效检验。所以改成用Fisher精确概率法进行计算,得到值为6.199,精确显著性(双侧)为0.785,即两组数据概率组成相似度达78.5%。
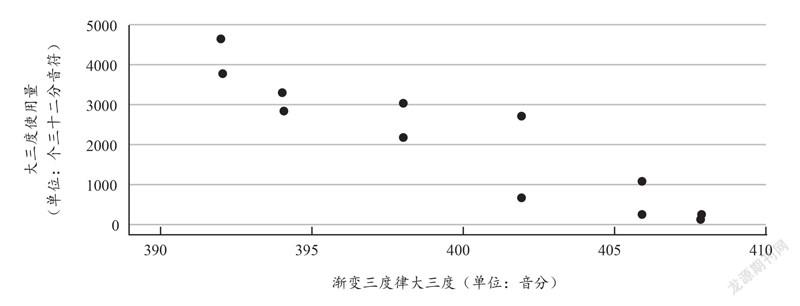
以渐变三度律的大三度音分值为自变量(X),莫扎特的大三度使用量做因变量(Y),绘制成散点图(图10)。通过线性回归分析,可求出Y=95145.190 - 232.736X的回归方程,莫扎特的斜率与贝多芬的斜率其实非常接近。在未经任何处理的情况下,R已经为0.925,拟合优度非常高,ANOVA分析见表9。
(二)18世纪下半叶普遍使用优律的可能性
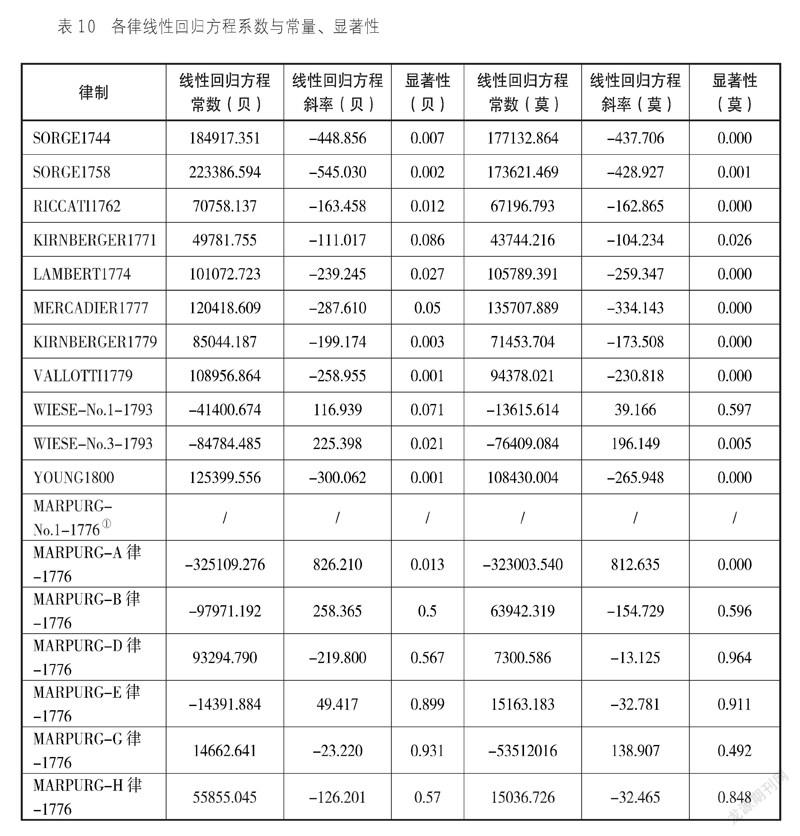
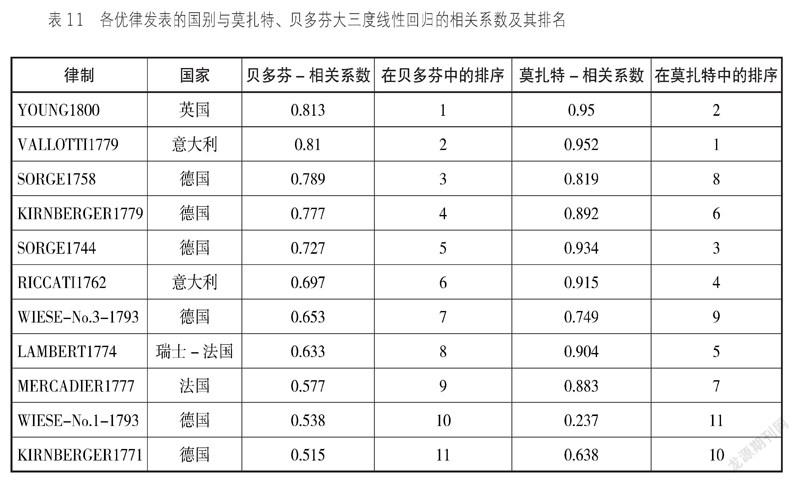
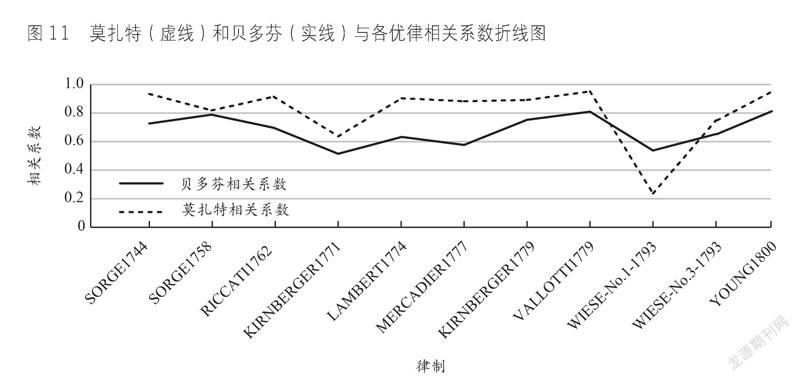
渐变三度律只是一个理想模型,并非实际存在,所以本节对18世纪下半叶真实存在的律制和莫扎特、贝多芬两人的数据分别进行线性回归,并作进一步分析。具体系数与常量、显著性及相关系数见表10、表11、图11。
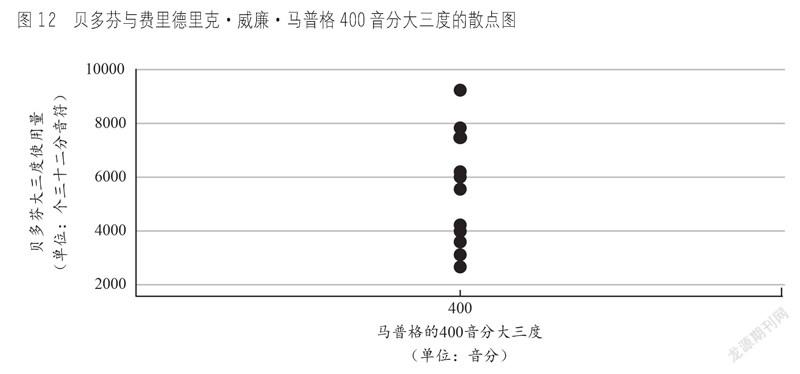
需要特别说明的是,费里德里克·威廉·马普格那些各大三度均为400音分的类平均律,由于只有一种大三度,是无法做线性回归的(见图12)。而且对其进行討论也是没有意义的,各大三度大小一致,抖拍一致,也就说明不存在任何差别,那么如何使用这些大三度就全凭作曲家意愿或其他因素的影响了。如果莫扎特、贝多芬用的是平均律,那么他根本不需要在乎哪些音程好听不好听、哪些调好用不好用,因为全部是一样的。
在表10、表11中,显著性及相关系数是各律与贝多芬大三度统计数据作线性回归优劣的参考值。显著性的值越小回归方程拟合度越好,显著性大于0.05表示拟合无效,相关系数越大说明两组数据相关可能性越大。可以从两点进行讨论:
其一,相关系数的高低与大三度布置的对称轴有关。YOUNG1800和VALLOTTI1779在两人数据的相关系数排名中均列前二,WIESE-No.1和KIRNBERGER1771均是最后两名。对比大三度音分值可知,前两者大三度的对称轴是“C”—“#F”,即C最小—大三度依次往两翼递增—F最大。而后两者则是对称中心明显不同,WIESE-No.1对称轴位于“E-B”—“A-E”,而KIRNBERGER1771对称轴则是“A-E”—“G”。除WIESE-No.3是完全相反的布置外,对称轴越接近“C”—“F”的优律相关系数越高。这说明在大三度的对称轴布置上,莫扎特和贝多芬有一致的想法。
其二,在两组数据各自的排序中,相关系数与律制发表年份有一定关系。贝多芬的第三、第四名是SORGE1758和KIRNBERGER1779,而莫扎特的第三、第四名是SORGE1744和
RICCATI1762, 前两者比后两者的发表年份更晚,不但与莫扎特、贝多芬两人的年代吻合,也显示出两人对大三度的使用与自身所处时代的律制更贴合。贝多芬的第五、第六名是SORGE1744和RICCATI1762,刚好就是莫扎特的第三、第四名,莫扎特的第六名刚好是贝多芬的第四名,VALLOTTI1779研究的时间是在1754年,这与乔治·安德烈亚斯·佐尔格律制的发表时间又非常接近,这显示出这些律制之间很可能有继承关系。
这是巧合还是必然?不同时间不同地方的作者调出相似的律制,不排除有巧合的可能性,但解释为来自18世纪音乐的听觉经验和理论积淀则更符合逻辑。在18世纪下半叶的欧洲音乐家们很有可能确如詹姆斯·默里·巴伯认为的那样,有着相同的调律追求,但只是由于调律技术的问题而致使最终效果有微小的差异。这十分耐人寻味。
余 论
从18世纪下半叶关于音律的历史材料看,平均律在当时并未成为泛用标准,支持优律的人更多。优律中有某些大三度更接近纯律大三度,其他大三度则根据一定的对称轴和斜率有序渐变。统计显示,莫扎特19首钢琴奏鸣曲、贝多芬32首钢琴奏鸣曲的大三度使用量呈现出某些大三度更常用的“山形”趋势,与大三度的大小成反比,与优律的大三度渐变存在高相关。与18世纪下半叶各优律大三度音分值的线性回归表明,当时音乐家们对大三度对称轴的布置有相同的追求,而且律制之间有继承的可能性很大。笔者认为,虽然暂未有充分的材料证明莫扎特、贝多芬使用的是哪一种优律,但从他们的作品中确实看到了优律的影子。
变化的大三度让优律具有了平均律所没有的调性色彩对比,听觉效果与平均律也会有所不同。现代学者已经开始关注用优律来演奏贝多芬钢琴作品的效果,如威廉·卡瓦根①认为用基恩贝尔格第Ⅲ律来演奏贝多芬《迪亚贝利变奏曲》特别合适,他讶异于非平均律在现代钢琴上也能有如此明显的效果;调音与调律专家马克·林德利在《新格罗夫音乐与音乐家辞典》中写道,“(Mercadier1776、Thomas Young1800、Lambert1774等)这些精良的律制通常是最适合用于18世纪晚期音乐的”①。像某些律制的降
A大调中,D音因为它偏低的音高再加上与C音的密切关系,听上去会特别温柔。林德利认为,这样的色彩能为如贝多芬钢琴奏鸣曲《悲怆》的柔板乐章这类用了许多降号的作品带来难以想象的美感。Chuan C. Chang提出,贝多芬钢琴奏鸣曲《月光》的第一乐章、《华尔斯坦》的第三乐章是能考察基恩贝尔格第Ⅱ律和平均律之异同的作品。②笔者也亲自尝试在用布拉德利·莱曼构建的巴赫优律来调律的钢琴上演奏贝多芬的奏鸣曲《春天》(为小提琴和钢琴而作),确实有和平均律截然不同的听觉体验。③所以,我们可以尝试基于优律来思考、理解古典主义时期的键盘作品,特别是莫扎特,从数据看,他与优律的关系甚至比贝多芬更为密切。
① Herbert Anton Kellner,“Baroque temperament,” 详见http://plaza.ufl.edu/wnb/baroque_temperament.htm,访问日期:2022年2月22日;同见李玫:《东西方乐律学研究及发展历程》,中央音乐学院出版社,2007,第184页,注①。
② John Barnes,“Bach’s keyboard temperament: Internal evidence from the ‘well-tempered clavier’,” Early Music,vii/2 (1979): 236-249.
③ Mark Lindley,“Bach’s temperament,” Early Music,xxxx/1(2012): 167.
④ Bradley Lehman,“Bach’s extraordinary temperament: our Rosetta Stone-1,” Early Music,xxxiii/1(2005): 3-23 及Bradley Lehman,“Bach’s extraordinary temperament: our Rosetta Stone-2,” Early Music,xxxiii/2(2005): 211-31.
⑤ John Charles Francis,“The Keyboard Temperament of J. S. Bach,”Eunomios,06/25/2004.
① Georg Andreas Sorge(1703—1778)是18世紀德国的理论家、管风琴家和作曲家。他在1747年加入了米兹勒社团,同年约翰·塞巴斯蒂安·巴赫也加入该社团。
② Willem Kroesbergen et al.,“18th century quotations relating to J.S. Bach’s temperament,” retrieved from https://www.huygens-fokker.org/docs/Kroesbergen_Bach_Temperament.pdf.
③ Bradley Lehman, “Variant of the temperament for vocal ensemble accompaniment,” http://www-personal.umich.edu/~bpl/larips/vocal.html.引用日期:2022年4月5日。
④ Giordano Riccati(1709—1790)是意大利的物理学家,他曾与瓦洛蒂有多次信件往来。
⑤ Mark Lindley,“Temperaments,§7: Irregular temperaments from 1680,”in THE NEW GROVE:Dictionary of Music and Musicians(second edition),ed.Stanley Sadie(Oxford:Oxford University Press,2001),湖南文艺出版社2012年引进出版,第25卷,第257页。
⑥ Johann Heinrich Lambert(1728—1777)出生于法国牟罗兹(当时瑞士的飞地),后卒于柏林,终年49岁,对数学、物理、哲学、天文学等学科做出了重要贡献。
⑦ Mark Lindley,“Well-tempered clavier,”in THE NEW GROVE:Dictionary of Music and Musicians(second edition),ed. Stanley Sadie,第27卷,第276页。
⑧ Friedrich Wilhelm Marpurg(1718—1795)是德国的作曲家、音乐批评家、音乐理论家、重要的调音调律学家。
⑨Friedrich Wilhelm Marpurg,Versuchüber die musikalische Temperatur(Breslau:Johann Friedrich Korn, 1776).
⑩Jean Baptiste Mercadier de Belesta (1750—1816),法国科学家、工程师、音乐理论家。
James Murray Barbour,Tuning and Temperament: A Historical Survey(East Lansing: Michigan State Press, 1951),p.168f. 詹姆斯·默里·巴伯转述了安东尼·舒尔曼-米瑟里的观点,其文献参见:Antoine Suremain-Missery,Théorie acoustico-musicale (Paris: François Didot, 1793).
Johann Philipp Kirnberger(1721—1783)是18世纪德国的理论家、音乐评论家、作曲家。
① Francesco Antonio Vallotti(1697—1780)是18世纪意大利的音乐理论家、作曲家和管风琴家。1722年成为帕多瓦圣安东尼奥教堂的管风琴师;1730年成为合唱乐长,在任长达50年。
②刘宝利:《谈巴赫〈十二平均律〉曲集的律制及键盘乐器的“十二非平均律”》,《乐府新声(沈阳音乐学院学报)》2009年第3期,第154~158页。
③Christian Ludwig Gustav Baron von Wiese (1732—1800),德国人,1732年出生于安斯巴赫,曾发表乐律理论及实践指导专著和若干论文。
④Christian Ludwig Gustav Baron von Wiese,Versuch über die logisch-mathematische Klangeintheilungs- Stimmungs- und Temperatur-Lehre(Dresden- Friedrichstadt: Wittwe Gerlach, 1793).
⑤James Murray Barbour,Tuning and Temperament: A Historical Survey,p.158f.
⑥ Thomas Young(1773—1829)是英國的物理学家。
⑦ Ross W. Duffin,How Equal Temperament Ruined Harmony (and Why You Should Care )(New York·London: W.W.Norton & Company, 2007),pp.84-85.
⑧Ross W.Duffin,How Equal Temperament Ruined Harmony (and Why You Should Care),p.65.
①各律按“造律者姓+序号(如有)+发表年份”标记。
②John O’Donnell,“Bach’s temperament, Occam’s razor, and the Neidhardt factor,”Early Music, xxxiv/4(2006): 625-633.
③根据“More Complicated Temperaments”“Variant of the temperament for vocal ensemble accompaniment”及“Circular 12-note temperaments”所述的调音法计算并移至实际音高。3篇文章分别参见:http://www.quadibloc.com/other/mus01.htm、http://www-personal.umich.edu/~bpl/larips/vocal.html及https://www.prismnet.com/~hmiller/music/warped-canon-12note.html。
④根据“Temperaments,§7: Irregular temperaments from 1680”的描述计算所得,音分值四舍五入取整。Stanley Sadie,THE NEW GROVE:Dictionary of Music and Musicians(second edition),第25卷,第257页。
⑤根据“Well-tempered clavier”表1中的调音法计算所得,音分值四舍五入取整。Stanley Sadie,THE NEW GROVE:Dictionary of Music and Musicians(second edition),第27卷,第276页,表1。
⑥James Murray Barbour,Tuning and Temperament: A Historical Survey,table 153.
⑦James Murray Barbour,Tuning and Temperament: A Historical Survey,table 132.
⑧根据“Well temperament”及“Temperaments Ⅶ: Werckmeister Ⅲ”的调音法计算所得,音分取整四舍五入。两篇文章分别参见:https://www.teoria.com/en/articles/temperaments/04-well-temperament.php及https://www.hpschd.nu/index.html?nav/nav-4.html&t/welcome.html&https://www.hpschd.nu/tech/tmp/werckmeister.html.
⑨刘宝利:《谈巴赫〈十二平均律〉曲集的律制及键盘乐器的“十二非平均律”》,《乐府新声(沈阳音乐学院学报)》,2009年第3期,第154~158页。
⑩James Murray Barbour,Tuning and Temperament: A Historical Survey,table 133-134。由于没有找到更多相关资料,在此仅罗列詹姆斯·默里·巴伯提及的两种。
James Murray Barbour,Tuning and Temperament: A Historical Survey,table 152.
James Murray Barbour,Tuning and Temperament: A Historical Survey,table 139(I律),144(G律),147(F律),154(D律),159(C律),161(B律),163(No.1),164(No.2),165(A律),166(E律),143(H律).
① C.P.E. Bach , Essay on the True Art of Playing Keyboard Instruments,trans.William J. Mitchell(New York: W. W. Norton & Company,1948), p.37.
②Heinrich Philipp Bossler, Elementarbuch der Tonkunst (Speier: gedrukt mit Enderesischen Schriften,1782),pp.xxiv-xxvi. 同见James Murray Barbour,Tuning and Temperament: A Historical Survey,p.49.
③ Alexander Ellis,“On the History of Musical Pitch,”Journal of the Society of Arts, xxviii(1880): 295.
④ Ross W. Duffin,How Equal Temperament Ruined Harmony(and Why You Should Care),p.85. 同見Constance S. Jolly,Beethoven as I knew Him,ed. D.W. MacArdle(Chapel Hill:The University of North Carolina Press,1966),p.367.
⑤ 费里德里克·威廉·马普格的No.1、No.2、C律、F律、I律所有大三度均为400音分,不重复罗列。
① 英文原文为“Multiple Division”,分别是把八度均分成17、19、22、24、31、34、36、41、42、43、50、53、55、56、65、67、74、81、98、105、112、117、118等份,涉及6种微分音键盘以及23种可以用于制作微分音键盘的八度均分体系。
② Owen Jorgensen,Tuning the Historical Temperaments By Ear(Marquette: Northern Michigan University Press,1977),pp.1-2.
③ Alexander J. Ellis,“Additions by the Translator,”in On the Sensations of Tone,ed. Hermann von Helmholtz (London: Longmans,Green,and CO.,1895),p.485,and Figure 1.7.
④ 这里的“跑调”指的是之于纯律的偏离。
⑤ James Murray Barbour,Tuning and Temperament: A Historical Survey,pp.178-184.
⑥ John Barnes, “Bach’s keyboard temperament: Internal evidence from the Well-Tempered Clavier,” Early Music, vii/2 (April 1979): 236-249.
① 详见www.humdrum.org .
② 详见https://www.humdrum.org/guide/ch02/, example 2.2 .
① 更详细的介绍参见www.humdrum.org .
② John Barnes,“Bach’s keyboard temperament: Internal evidence from the Well-Tempered Clavier,” Early Music, vii/2 (April 1979): 236-249.
③ Michèle Duguay,The Influence of Unequal Temperament on Chopin’s Piano Works. Schulich School of Music,McGill University,2016.
① 此节因涉及编程代码,为便于阅读,升降记号保留原有标记方式。
① 在kern数据库中,莫扎特钢琴奏鸣曲只有17首,缺失的K.533和K.547由笔者进行人工统计补上。
① James Murray Barbour, Tuning and Temperament: A Historical Survey, Chapter VII:181-184.
② 需要注意的是,这里的计算只是一个假设的理论方案,仅供参考。在古典时期没有能准确测量音分值的仪器,只能靠耳朵分辨。
① 实线示意渐变三度律各大三度之于该律中最纯大三度的音分偏离占总音分偏离的比例,虚线示意贝多芬钢琴奏鸣曲中各大三度的使用量占所有大三度使用总量之和的比例。
① Marpurg的No.1、No.2、C律、F律、I律所有大三度均为400音分,不重复罗列。
① William Carragan,“Beethoven: Diabelli variations: The record connoisseur's magazine,”American Record Guide(Nov.,1997): 60,99-101.
①Mark Lindley,“Temperaments,§7: Irregular temperaments from 1680,”in THE NEW GROVE:Dictionary of Music and Musicians(second edition),ed.Stanley Sadie,第25卷,第257页。
② Chaun C. Chang,Fundamentals of Piano Practice,p.235,http://www.pianopractice.org/book.pdf.
③ 余思韵:《21世纪初欧美学者再论“巴赫律”的英文论文选译及述评》,硕士学位论文,星海音乐学院,2019。
收稿日期:2022-04-19
作者简介:余思韵(1988— ),女,硕士,上海音乐学院音乐艺术研究院(音乐研究所)編译(上海 200031)。
